2020版高考艺考生文化课百日冲刺 第1讲 集合与常见逻辑用语(课件46张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第1讲 集合与常见逻辑用语(课件46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 12:26:46 | ||
图片预览







文档简介
课件46张PPT。第1讲 集合与常见逻辑用语1.集合的有关概念
(1)集合元素的特性:确定性、互异性、无序性.
(2)集合与元素的关系:若a属于集合A,记作a∈A;若b不属于集合A,记作b?A.
(3)集合的表示方法:列举法、描述法、图示法.
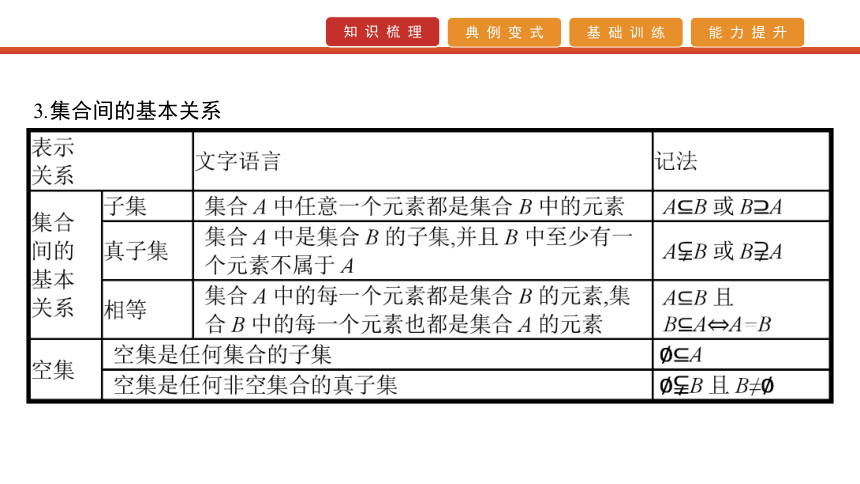
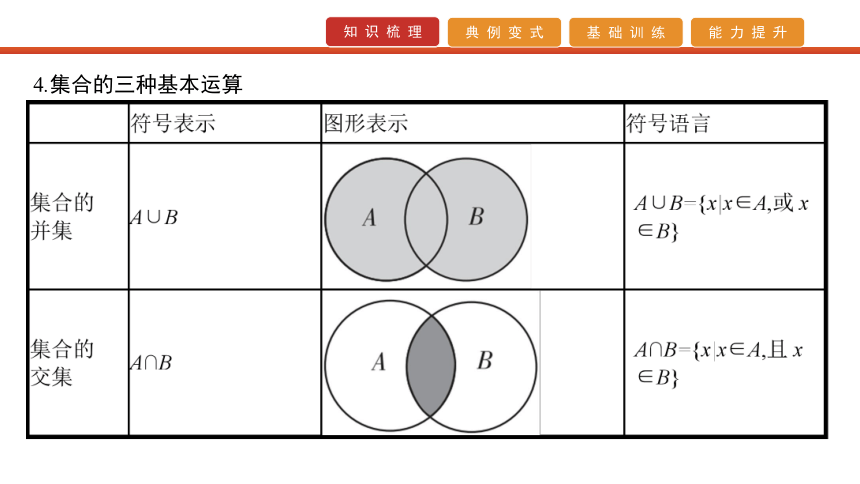
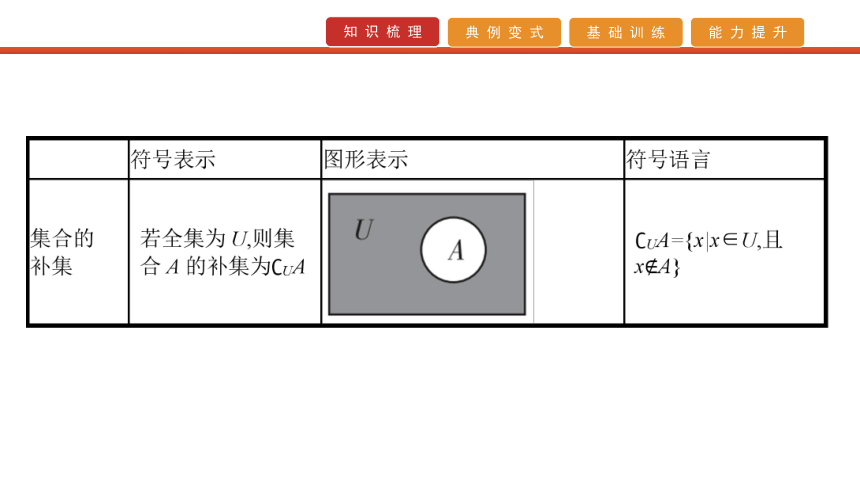
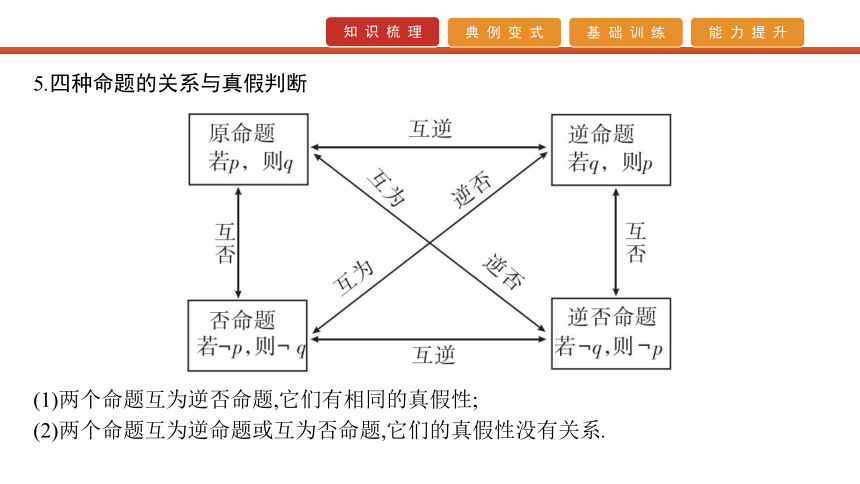
2.常用数集及记法3.集合间的基本关系 4.集合的三种基本运算 5.四种命题的关系与真假判断 (1)两个命题互为逆否命题,它们有相同的真假性;
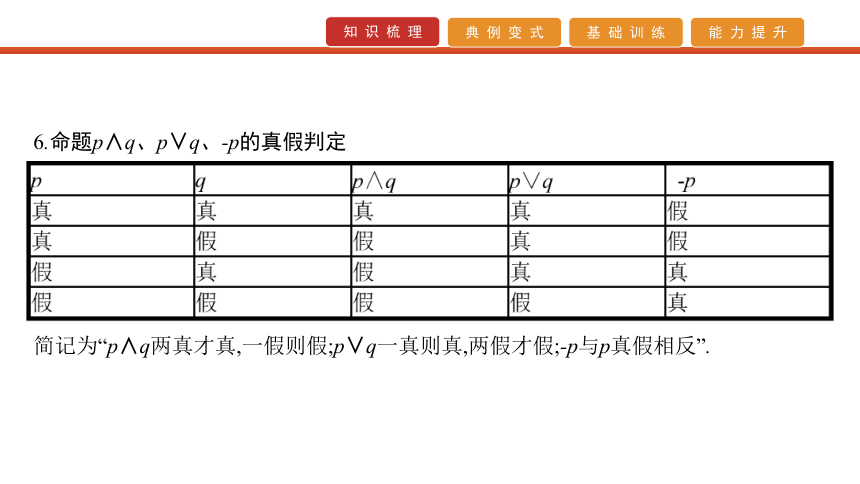
(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.6.命题p∧q、p∨q、-p的真假判定 简记为“p∧q两真才真,一假则假;p∨q一真则真,两假才假;-p与p真假相反”. 7.量词
(1)全称量词和存在量词(2)全称命题和特称命题 8.条件问题
(1)充分条件、必要条件与充要条件(2)充要条件常用的三种判断方法
①定义法:直接判断若p则q、若q则p的真假.
②等价法:利用A?B与 B? A,B?A与 A? B,A?B与 B? A的等价关系,对于条件或结论是否定式的命题,一般运用等价法.
③利用集合间的包含关系判断:若A?B,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.
(3)判断充要条件需注意三点
①要分清条件与结论分别是什么;
②要从充分性、必要性两个方面进行判断;
③直接判断比较困难时,可举出反例说明.题型一 集合的基本概念
【例1】 (1)设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M中的元素个数为( )
A.3 B.4
C.5 D.6
(2)若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=( )【解析】 (1)因为集合M中的元素x=a+b,a∈A,b∈B,所以当b=4,a=1,2,3时,x=5,6,7;
当b=5,a=1,2,3时,x=6,7,8.
由集合元素的互异性,可知x=5,6,7,8.
即M={5,6,7,8},共有4个元素.
(2)若集合A中只有一个元素,则方程ax2-3x+2=0只有一个实数根或有两个相等的实数根.【答案】(1)B (2)D 【规律方法】与集合中的元素有关的问题的求解策略
(1)确定集合中的元素是什么,即集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合中元素的个数,要注意检验集合是否满足元素的互异性.变式训练一
1.已知集合A={x|x∈Z,且 ∈Z},则集合A中的元素个数为( )
A.2 B.3 C.4 D.52.已知集合A={m+2,2m2+m},若3∈A,则m的值为 .? C 所以x的值分别为3,5,-1,1,故集合A中的元素个数为4. 题型二 集合间的基本关系
【例2】 (1)已知集合A={x|4≤2x≤16},B[a,b],若A?B,则实数a-b的取值范围是 .?
(2)已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B?A,则实数m的取值范围为 .?
【解析】 (1)集合A={x|4≤2x≤16}={x|22≤2x≤24}={x|2≤x≤4}=[2,4].
因为A?B,所以a≤2,b≥4.所以a-b≤2-4=-2,即实数a-b的取值范围是(-∞,-2].
(2)因为B?A,所以①若B=?,则2m-1【答案】 (1)(-∞,-2] (2)(-∞,3]【规律方法】
1.集合间基本关系的两种判定方法
(1)化简集合,从表达式中寻找两集合的关系.
(2)用列举法(或图示法等)表示各个集合,从元素(或图形)中寻找关系.
2.根据集合间的关系求参数的方法,已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素或区间端点间的关系,进而转化为参数满足的关系,解决这类问题常常要合理利用数轴、Venn图化抽象为直观进行求解.
易错警示:B?A(A≠?),应分B=?和B≠?两种情况讨论.变式训练二
1.已知集合A={x|1≤x<5},C={x|-a当m>0时,因为A={x|-1集合的基本运算是历年各地高考的热点,每年必考,常和不等式的解集、函数的定义域、值域相结合命题,主要以选择题的形式出现.试题多为低档题.
高考对集合运算的考查主要从以下三个角度命题:①求集合间的交或并运算;②求集合的交、并、补的混合运算;③已知集合的运算结果求参数的值(范围).【例3】 (1)(2019·桂林模拟)已知集合M={x|-1A.M∪N={-1,1,3}
B.M∪N={x|-1≤x<3}
C.M∩N={-1}
D.M∩N={x|-1(2)设集合A={x|-1≤x<2},B={x|xA.-12
C.a≥-1 D.a>-1
(3)(2019·厦门模拟)已知集合A={x|xA.a≤1 B.a<1
C.a≥2 D.a>2【解析】 (1)M∪N={x|-1≤x<3},M∩N={1},故选B.
(2)由A∩B≠?知,集合A,B有公共元素,作出数轴,如图所示:
易知a>-1,故选D.
(3)B={x|1【答案】(1)B (2)D (3)C【规律方法】解决集合运算问题需注意以下三点
(1)看元素组成,集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)看集合能否化简,集合能化简的先化简,再研究其关系并进行运算,可使问题简单明了,易于求解.
(3)要借助Venn图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,并注意端点值的取舍.变式训练三
1.(2017·北京卷)若集合A={x|-23},则A∩B=( )
A.{x|-2B.{x|-2C.{x|-1D.{x|1A.{1}
B.{3,5}
C.{1,2,4,6}
D.{1,2,3,4,5}3.(2019·东北三省四市联考)设集合A={x||x|<1},B={x|x(x-3)<0},则A∪B=( )
A.(-1,0) B.(0,1)
C.(-1,3) D.(1,3)C 【解析】 因为U={1,2,3,4,5,6},P={1,3,5},所以?UP={2,4,6},因为Q={1,2,4},所以(?UP)∪Q={1,2,4,6}.【解析】 A={x|-1故选C.C 4.已知集合A={x|x2-5x-6<0},B={x|2x<1},则图中阴影部分表示的集合是 .?{x|0≤x<6} 【解析】 由x2-5x-6<0,解得-1由2x<1,解得x<0,所以B={x|x<0}.又图中阴影部分表示的集合为(?UB)∩A,
因为?UB={x|x≥0},所以(?UB)∩A={x|0≤x<6}.题型四 判断含逻辑词连接的命题的真假
【例4】 已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2,在命题①p∧q;②p∨q;③p∧(-q);④(-p)∨q中,真命题是( )
A.①③ B.①④
C.②③ D.②④
【解析】 p为真;对于命题q:若x>y,令x=1,y=-2,显然x2【答案】 C
【规律方法】“p∧q”“p∨q”“ p”等形式命题真假的判断步骤
(1)确定命题的构成形式.
(2)判断其中命题p,q的真假.
(3)依据“或”——一真即真,“且”——一假即假,“非”——真假相反,来确定“p∧q”“p∨q”“ p”等形式命题的真假.变式训练四
(2019·泰安模拟)已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )
A.p∧q B.p∧( q)
C.( p)∧q D.( p)∧( q)B 【解析】 ∵x>0,∴x+1>1,∴ln(x+1)>ln1=0.
∴命题p为真命题,∴ p为假命题.
∵a>b,取a=1,b=-2,而12=1,(-2)2=4,此时a2∴命题q为假命题,∴ q为真命题.
∴p∧q为假命题,p∧ q为真命题, p∧q为假命题, p∧ q为假命题.故选B.题型五 充分条件与必要条件的判定
【例5】 (1)(2018·北京卷)设a,b,c,d是非零实数,则“ad=bc”是“a,b,c,d成等比数列”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
(2)设集合M={x|0A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件(3)设命题p:(4x-3)2≤1,命题q:x2-(2m+1)x+m(m+1)≤0,若 p是 q的必要不充分条件,则实数m的取值范围是( )要而不充分条件,故选B.
(2)条件与结论都是否定形式,可转化为判断“m∈N”是“m∈M”的什么条件.由N?M知,“m∈N”是“m∈M”的充分不必要条件,从而“m?M”是“m?N”的充分不必要条件,故选A.由x2-(2m+1)x+m(m+1)≤0得m≤x≤m+1,即q:m≤x≤m+1.
由 p是 q的必要不充分条件知,p是q的充分不必要条件,【答案】(1)B (2)A (3)A 【规律方法】充分条件和必要条件的三种判断方法
(1)定义法:可按照以下三个步骤进行
①确定条件p是什么,结论q是什么;
②尝试由条件p推结论q,由结论q推条件p;
③确定条件p和结论q的关系.
(2)等价转换法:对于含否定形式的命题,如﹁p是﹁q的什么条件,利用原命题与逆否命题的等价性,可转化为求q是p的什么条件.
(3)集合法:根据p,q成立时对应的集合之间的包含关系进行判断.
【易错警示】判断条件之间的充要关系要注意条件之间的语句描述,比如正确理解“p的一个充分不必要条件是q”应是“q推出p,而p不能推出q”.变式训练五
1.(2018·合肥一模)“x>2”是“x2+2x-8>0”成立的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件B 【解析】 由x2+2x-8>0,可解得x<-4或x>2,所以“x>2”是“x2+2x-8>0”成立的充分不必要条件,故选B.2.若“x>2m2-3”是“-1A.[-1,1] B.[-1,0]
C.[1,2] D.[-1,2]3.(2019·常德一中月考)若“x2-x-6>0”是“x>a”的必要不充分条件,则a的最小值为 .?A 【解析】 由题意知(-1,4)?(2m2-3,+∞),
∴2m2-3≤-1,解得-1≤m≤1,故选A.3 【解析】 由x2-x-6>0,解得x<-2或x>3.因为“x2-x-6>0”是“x>a”的必要不充分条件,所以{x|x>a}是{x|x<-2或x>3}的真子集,即a≥3,故a的最小值为3.题型六 全(特)称命题的否定(高频考点)
全称命题与特称命题是高考的常考内容,多和其他数学知识相结合命题,常以选择题、填空题的形式出现.
高考对全称命题、特称命题的考查主要从以下两个角度命题:①判断全称命题、特称命题的真假性;②全称命题、特称命题的否定.?变式训练六
1.命题“对任意x∈R,都有x2≥ln 2”的否定为( )
A.对任意x∈R,都有x2B.不存在x∈R,使得x2m”是真命题,则m的值可以是( )A 1.(2019·山东潍坊月考)已知集合M={x|x2-x-2=0},N={-1,0},则M∪N=( )
A.{-1,0,2} B.{-1}
C.{0} D.?2.(2019·广东惠州模拟)已知集合M={0,1,2,3},N={x|x2=1},则M∩N=( )
A.{1} B.{-1,1}
C.{1,0} D.{-1,1,0}A 【解析】 集合M={x|x2-x-2=0}={x|x=2或x=-1}={-1,2},N={-1,0},则M∪N={-1,0,2}.【解析】 N={x|x2=1}={-1,1},M∩N={1}. A 是( )
A.{x|-3B.{x|-3C.{x|-1≤x<0}
D.{x|-10},B={x|x-a≤0},若?UB?A,则实数a的取值范围是( )
A.(-∞,1) B.(-∞,2]
C.[1,+∞) D.[2,+∞)6.(2019·湖南长郡中学联考)若x>2m2-3是-1A.[-3,3] B.(-∞,-3]∪[3,+∞)
C.(-∞,-1)∪[1,+∞) D.[-1,1]D 【解析】 因为x2-3x+2>0,所以x>2或x<1.所以A={x|x>2或x<1},因为B={x|x≤a},所以?UB={x|x>a}.因为?∪B?A,借助数轴可知a≥2,故选D.【解析】 ∵“x>2m2-3”是“-1A.a≥4 B.a>4
C.a≥1 D.a>18.(2018·福州质检)已知命题p:?x1,x2∈R,[f(x2)-f(x1)](x2-x1)≥0,则 p是( )
A.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)≤0
B.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)≤0
C.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0
D.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0B 【解析】 要使“对任意x∈[1,2),x2-a≤0”为真命题,只需要a≥4,所以a>4是命题为真的充分不必要条件.C 【解析】 已知全称命题p:?x1,x2∈R,[f(x2)-f(x1)]·(x2-x1)≥0,则 p:?x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0,故选C.为真的是( )
A.p∧( q) B.( p)∧q
C.p∧q D.( p)∨q10.已知集合A={x|1≤x<5},C={x|-a2x,当x=4时,42=24,∴命题q为假.所以p∧( q)为真,故选A.(-∞,-1] 【解析】 因为C∩A=C,所以C?A. 1.设全集U=R,集合A={x|x≤1或x≥3},集合B={x|kA.k<0 B.k<2
C.0∵B={x|k∴k≤0,∴当B∩(?UA)≠?时,0A.[2,+∞) B.(2,+∞)
C.[1,+∞) D.(-∞,-1]B 【解析】 由q:(x+1)(2-x)<0,得x<-1或x>2,又p是q的充分不必要条件,所以k>2,即实数k的取值范围是(2,+∞),故选B.3.(2018·张掖第一次诊断)下列说法正确的是( ) A 件,故A正确;由p∧q为真命题,知p,q均为真命题,所以p∨q为真命题,反之,由p∨q为真命题,得p,q至少有一个为真命题,所以p∧q不一定为真命题,所以“p∧q为真命题”是“p∨q4.已知集合A={x∈N|x2-2x-3≤0},B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素数字之和为 .?21 【解析】 由x2-2x-3≤0,x∈N,得(x+1)(x-3)≤0,x∈N,得A={0,1,2,3}.因为A*B={x|x=x1+x2,x1∈A,x2∈B},所以A*B中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A*B={1,2,3,4,5,6},所以A*B中的所有元素数字之和为21.
(1)集合元素的特性:确定性、互异性、无序性.
(2)集合与元素的关系:若a属于集合A,记作a∈A;若b不属于集合A,记作b?A.
(3)集合的表示方法:列举法、描述法、图示法.
2.常用数集及记法3.集合间的基本关系 4.集合的三种基本运算 5.四种命题的关系与真假判断 (1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.6.命题p∧q、p∨q、-p的真假判定 简记为“p∧q两真才真,一假则假;p∨q一真则真,两假才假;-p与p真假相反”. 7.量词
(1)全称量词和存在量词(2)全称命题和特称命题 8.条件问题
(1)充分条件、必要条件与充要条件(2)充要条件常用的三种判断方法
①定义法:直接判断若p则q、若q则p的真假.
②等价法:利用A?B与 B? A,B?A与 A? B,A?B与 B? A的等价关系,对于条件或结论是否定式的命题,一般运用等价法.
③利用集合间的包含关系判断:若A?B,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.
(3)判断充要条件需注意三点
①要分清条件与结论分别是什么;
②要从充分性、必要性两个方面进行判断;
③直接判断比较困难时,可举出反例说明.题型一 集合的基本概念
【例1】 (1)设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M中的元素个数为( )
A.3 B.4
C.5 D.6
(2)若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=( )【解析】 (1)因为集合M中的元素x=a+b,a∈A,b∈B,所以当b=4,a=1,2,3时,x=5,6,7;
当b=5,a=1,2,3时,x=6,7,8.
由集合元素的互异性,可知x=5,6,7,8.
即M={5,6,7,8},共有4个元素.
(2)若集合A中只有一个元素,则方程ax2-3x+2=0只有一个实数根或有两个相等的实数根.【答案】(1)B (2)D 【规律方法】与集合中的元素有关的问题的求解策略
(1)确定集合中的元素是什么,即集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合中元素的个数,要注意检验集合是否满足元素的互异性.变式训练一
1.已知集合A={x|x∈Z,且 ∈Z},则集合A中的元素个数为( )
A.2 B.3 C.4 D.52.已知集合A={m+2,2m2+m},若3∈A,则m的值为 .? C 所以x的值分别为3,5,-1,1,故集合A中的元素个数为4. 题型二 集合间的基本关系
【例2】 (1)已知集合A={x|4≤2x≤16},B[a,b],若A?B,则实数a-b的取值范围是 .?
(2)已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B?A,则实数m的取值范围为 .?
【解析】 (1)集合A={x|4≤2x≤16}={x|22≤2x≤24}={x|2≤x≤4}=[2,4].
因为A?B,所以a≤2,b≥4.所以a-b≤2-4=-2,即实数a-b的取值范围是(-∞,-2].
(2)因为B?A,所以①若B=?,则2m-1
1.集合间基本关系的两种判定方法
(1)化简集合,从表达式中寻找两集合的关系.
(2)用列举法(或图示法等)表示各个集合,从元素(或图形)中寻找关系.
2.根据集合间的关系求参数的方法,已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素或区间端点间的关系,进而转化为参数满足的关系,解决这类问题常常要合理利用数轴、Venn图化抽象为直观进行求解.
易错警示:B?A(A≠?),应分B=?和B≠?两种情况讨论.变式训练二
1.已知集合A={x|1≤x<5},C={x|-a
高考对集合运算的考查主要从以下三个角度命题:①求集合间的交或并运算;②求集合的交、并、补的混合运算;③已知集合的运算结果求参数的值(范围).【例3】 (1)(2019·桂林模拟)已知集合M={x|-1
B.M∪N={x|-1≤x<3}
C.M∩N={-1}
D.M∩N={x|-1
C.a≥-1 D.a>-1
(3)(2019·厦门模拟)已知集合A={x|x
C.a≥2 D.a>2【解析】 (1)M∪N={x|-1≤x<3},M∩N={1},故选B.
(2)由A∩B≠?知,集合A,B有公共元素,作出数轴,如图所示:
易知a>-1,故选D.
(3)B={x|1
(1)看元素组成,集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)看集合能否化简,集合能化简的先化简,再研究其关系并进行运算,可使问题简单明了,易于求解.
(3)要借助Venn图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,并注意端点值的取舍.变式训练三
1.(2017·北京卷)若集合A={x|-2
A.{x|-2
B.{3,5}
C.{1,2,4,6}
D.{1,2,3,4,5}3.(2019·东北三省四市联考)设集合A={x||x|<1},B={x|x(x-3)<0},则A∪B=( )
A.(-1,0) B.(0,1)
C.(-1,3) D.(1,3)C 【解析】 因为U={1,2,3,4,5,6},P={1,3,5},所以?UP={2,4,6},因为Q={1,2,4},所以(?UP)∪Q={1,2,4,6}.【解析】 A={x|-1
因为?UB={x|x≥0},所以(?UB)∩A={x|0≤x<6}.题型四 判断含逻辑词连接的命题的真假
【例4】 已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2,在命题①p∧q;②p∨q;③p∧(-q);④(-p)∨q中,真命题是( )
A.①③ B.①④
C.②③ D.②④
【解析】 p为真;对于命题q:若x>y,令x=1,y=-2,显然x2
【规律方法】“p∧q”“p∨q”“ p”等形式命题真假的判断步骤
(1)确定命题的构成形式.
(2)判断其中命题p,q的真假.
(3)依据“或”——一真即真,“且”——一假即假,“非”——真假相反,来确定“p∧q”“p∨q”“ p”等形式命题的真假.变式训练四
(2019·泰安模拟)已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )
A.p∧q B.p∧( q)
C.( p)∧q D.( p)∧( q)B 【解析】 ∵x>0,∴x+1>1,∴ln(x+1)>ln1=0.
∴命题p为真命题,∴ p为假命题.
∵a>b,取a=1,b=-2,而12=1,(-2)2=4,此时a2
∴p∧q为假命题,p∧ q为真命题, p∧q为假命题, p∧ q为假命题.故选B.题型五 充分条件与必要条件的判定
【例5】 (1)(2018·北京卷)设a,b,c,d是非零实数,则“ad=bc”是“a,b,c,d成等比数列”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
(2)设集合M={x|0
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件(3)设命题p:(4x-3)2≤1,命题q:x2-(2m+1)x+m(m+1)≤0,若 p是 q的必要不充分条件,则实数m的取值范围是( )要而不充分条件,故选B.
(2)条件与结论都是否定形式,可转化为判断“m∈N”是“m∈M”的什么条件.由N?M知,“m∈N”是“m∈M”的充分不必要条件,从而“m?M”是“m?N”的充分不必要条件,故选A.由x2-(2m+1)x+m(m+1)≤0得m≤x≤m+1,即q:m≤x≤m+1.
由 p是 q的必要不充分条件知,p是q的充分不必要条件,【答案】(1)B (2)A (3)A 【规律方法】充分条件和必要条件的三种判断方法
(1)定义法:可按照以下三个步骤进行
①确定条件p是什么,结论q是什么;
②尝试由条件p推结论q,由结论q推条件p;
③确定条件p和结论q的关系.
(2)等价转换法:对于含否定形式的命题,如﹁p是﹁q的什么条件,利用原命题与逆否命题的等价性,可转化为求q是p的什么条件.
(3)集合法:根据p,q成立时对应的集合之间的包含关系进行判断.
【易错警示】判断条件之间的充要关系要注意条件之间的语句描述,比如正确理解“p的一个充分不必要条件是q”应是“q推出p,而p不能推出q”.变式训练五
1.(2018·合肥一模)“x>2”是“x2+2x-8>0”成立的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件B 【解析】 由x2+2x-8>0,可解得x<-4或x>2,所以“x>2”是“x2+2x-8>0”成立的充分不必要条件,故选B.2.若“x>2m2-3”是“-1
C.[1,2] D.[-1,2]3.(2019·常德一中月考)若“x2-x-6>0”是“x>a”的必要不充分条件,则a的最小值为 .?A 【解析】 由题意知(-1,4)?(2m2-3,+∞),
∴2m2-3≤-1,解得-1≤m≤1,故选A.3 【解析】 由x2-x-6>0,解得x<-2或x>3.因为“x2-x-6>0”是“x>a”的必要不充分条件,所以{x|x>a}是{x|x<-2或x>3}的真子集,即a≥3,故a的最小值为3.题型六 全(特)称命题的否定(高频考点)
全称命题与特称命题是高考的常考内容,多和其他数学知识相结合命题,常以选择题、填空题的形式出现.
高考对全称命题、特称命题的考查主要从以下两个角度命题:①判断全称命题、特称命题的真假性;②全称命题、特称命题的否定.?变式训练六
1.命题“对任意x∈R,都有x2≥ln 2”的否定为( )
A.对任意x∈R,都有x2
A.{-1,0,2} B.{-1}
C.{0} D.?2.(2019·广东惠州模拟)已知集合M={0,1,2,3},N={x|x2=1},则M∩N=( )
A.{1} B.{-1,1}
C.{1,0} D.{-1,1,0}A 【解析】 集合M={x|x2-x-2=0}={x|x=2或x=-1}={-1,2},N={-1,0},则M∪N={-1,0,2}.【解析】 N={x|x2=1}={-1,1},M∩N={1}. A 是( )
A.{x|-3
D.{x|-1
A.(-∞,1) B.(-∞,2]
C.[1,+∞) D.[2,+∞)6.(2019·湖南长郡中学联考)若x>2m2-3是-1
C.(-∞,-1)∪[1,+∞) D.[-1,1]D 【解析】 因为x2-3x+2>0,所以x>2或x<1.所以A={x|x>2或x<1},因为B={x|x≤a},所以?UB={x|x>a}.因为?∪B?A,借助数轴可知a≥2,故选D.【解析】 ∵“x>2m2-3”是“-1
C.a≥1 D.a>18.(2018·福州质检)已知命题p:?x1,x2∈R,[f(x2)-f(x1)](x2-x1)≥0,则 p是( )
A.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)≤0
B.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)≤0
C.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0
D.?x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0B 【解析】 要使“对任意x∈[1,2),x2-a≤0”为真命题,只需要a≥4,所以a>4是命题为真的充分不必要条件.C 【解析】 已知全称命题p:?x1,x2∈R,[f(x2)-f(x1)]·(x2-x1)≥0,则 p:?x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0,故选C.为真的是( )
A.p∧( q) B.( p)∧q
C.p∧q D.( p)∨q10.已知集合A={x|1≤x<5},C={x|-a
C.0
C.[1,+∞) D.(-∞,-1]B 【解析】 由q:(x+1)(2-x)<0,得x<-1或x>2,又p是q的充分不必要条件,所以k>2,即实数k的取值范围是(2,+∞),故选B.3.(2018·张掖第一次诊断)下列说法正确的是( ) A 件,故A正确;由p∧q为真命题,知p,q均为真命题,所以p∨q为真命题,反之,由p∨q为真命题,得p,q至少有一个为真命题,所以p∧q不一定为真命题,所以“p∧q为真命题”是“p∨q4.已知集合A={x∈N|x2-2x-3≤0},B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素数字之和为 .?21 【解析】 由x2-2x-3≤0,x∈N,得(x+1)(x-3)≤0,x∈N,得A={0,1,2,3}.因为A*B={x|x=x1+x2,x1∈A,x2∈B},所以A*B中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A*B={1,2,3,4,5,6},所以A*B中的所有元素数字之和为21.
同课章节目录
