2020版高考艺考生文化课百日冲刺 第7讲 不等式及其应用(课件:40张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第7讲 不等式及其应用(课件:40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览


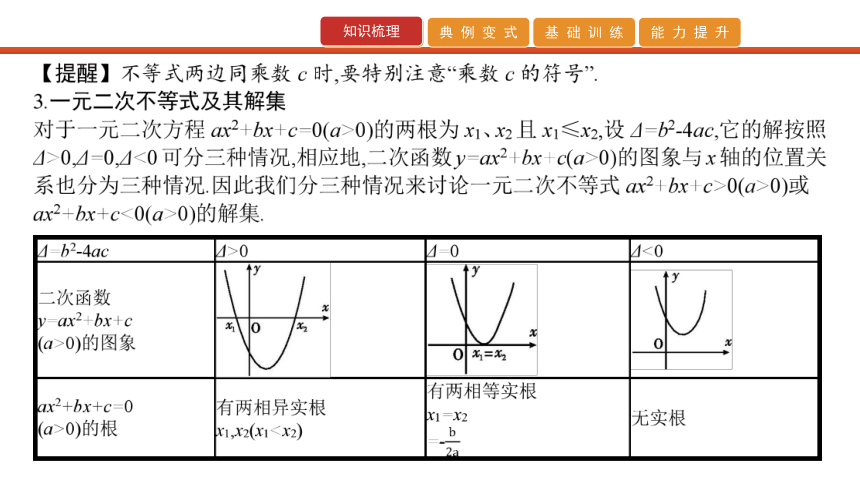









文档简介
课件40张PPT。第7讲 不等式及其应用【答案】(1)B (2)C (3)A (4)(-π,2π) 【规律方法】利用不等式的性质判断正误及求代数式的范围的方法
(1)利用不等式的范围判断正误时,常用两种方法:
一是直接使用不等式的性质逐个验证;二是利用特殊值法排除错误答案.
(2)比较大小常用的方法
①作差(商)法:作差(商)?变形?判断,
②构造函数法:利用函数的单调性比较大小,
③中间量法:利用中间量法比较两式大小,一般选取0或1作为中间量.
(3)由a0,y>0,x+3y+xy=9,则x+3y的最小值为 ?【答案】 6 【规律方法】
(1)利用基本不等式求最值的两种思路:利用基本不等式解决条件最值的关键是构造和为定值或积为定值,主要有两种思路:①对条件使用基本不等式,建立所求目标函数的不等式求解.常用的方法有:拆项法、变系数法、凑因子法、换元法、整体代换法等.②条件变形,进行“1”的代换求目标函数最值.
(2)条件最值的求法:条件最值的求解通常有三种方法:一是消元法,即根据条件建立两个量之间的函数关系,然后代入代数式转化为函数的最值求解;二是将条件灵活变形,利用常数代换的方法构造和或积为常数的式子,然后利用基本不等式求解最值;三是对条件使用基本不等式,建立所求目标函数的不等式求解.
【注意】①应用基本不等式解题一定要注意应用的前提:“一正”“二定”“三相等”.所谓“一正”是指正数,“二定”是指应用基本不等式求最值时,和或积为定值,“三相等”是指满足等号成立的条件.②尽量避免多次使用基本不等式,若必须多次使用,一定要保证等号成立的条件一致.【解析】 设log3a=log4b=t,则a=3t,b=4t;当t<0时,y=xt在(0,+∞)上为减函数,则b0时,y=xt在(0,+∞)上为增函数,则b>a>1;当t=0时,则b=a=1;故选②④⑤.
(1)利用不等式的范围判断正误时,常用两种方法:
一是直接使用不等式的性质逐个验证;二是利用特殊值法排除错误答案.
(2)比较大小常用的方法
①作差(商)法:作差(商)?变形?判断,
②构造函数法:利用函数的单调性比较大小,
③中间量法:利用中间量法比较两式大小,一般选取0或1作为中间量.
(3)由a
(1)利用基本不等式求最值的两种思路:利用基本不等式解决条件最值的关键是构造和为定值或积为定值,主要有两种思路:①对条件使用基本不等式,建立所求目标函数的不等式求解.常用的方法有:拆项法、变系数法、凑因子法、换元法、整体代换法等.②条件变形,进行“1”的代换求目标函数最值.
(2)条件最值的求法:条件最值的求解通常有三种方法:一是消元法,即根据条件建立两个量之间的函数关系,然后代入代数式转化为函数的最值求解;二是将条件灵活变形,利用常数代换的方法构造和或积为常数的式子,然后利用基本不等式求解最值;三是对条件使用基本不等式,建立所求目标函数的不等式求解.
【注意】①应用基本不等式解题一定要注意应用的前提:“一正”“二定”“三相等”.所谓“一正”是指正数,“二定”是指应用基本不等式求最值时,和或积为定值,“三相等”是指满足等号成立的条件.②尽量避免多次使用基本不等式,若必须多次使用,一定要保证等号成立的条件一致.【解析】 设log3a=log4b=t,则a=3t,b=4t;当t<0时,y=xt在(0,+∞)上为减函数,则b
同课章节目录
