2020版高考艺考生文化课百日冲刺 第17讲 函数与方程(课件)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第17讲 函数与方程(课件) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 12:35:49 | ||
图片预览






文档简介
课件29张PPT。第17讲 函数与方程1.函数的零点
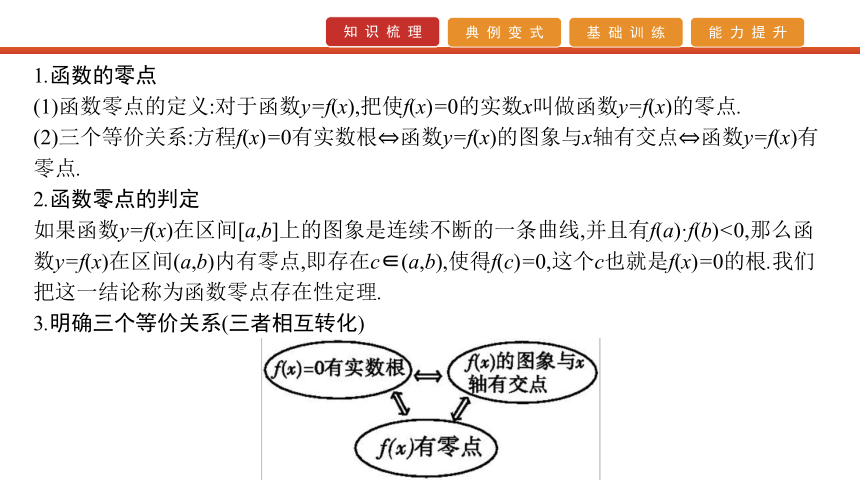
(1)函数零点的定义:对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.
(2)三个等价关系:方程f(x)=0有实数根?函数y=f(x)的图象与x轴有交点?函数y=f(x)有零点.
2.函数零点的判定
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是f(x)=0的根.我们把这一结论称为函数零点存在性定理.
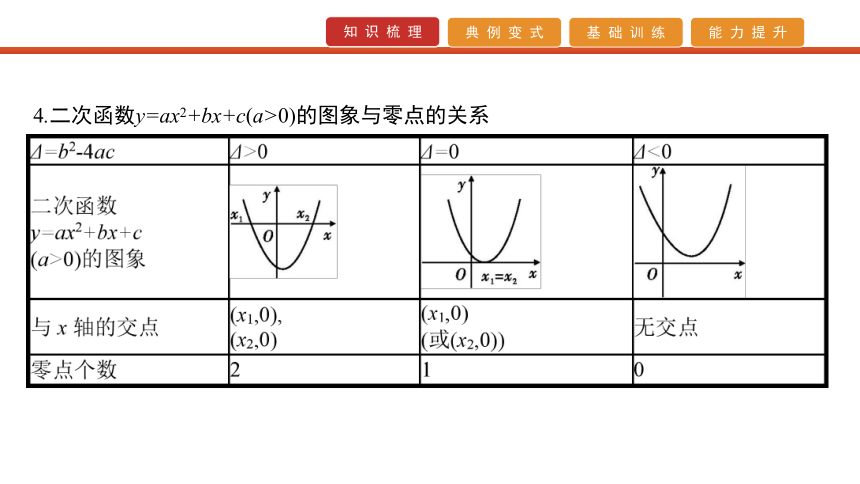
3.明确三个等价关系(三者相互转化)4.二次函数y=ax2+bx+c(a>0)的图象与零点的关系 题型一 函数零点所在区间的判断
【例1】 (1)函数f(x)=ln x- 的零点所在的大致区间是( )
A.(1,2) B.(2,3)
C.(1,e)和(3,4) D.(e,+∞)
(2)设f(x)=0.8x-1,g(x)=ln x,则函数h(x)=f(x)-g(x)存在的零点一定位于下列哪个区间( )
A.(0,1) B.(1,2)
C.(2,e) D.(e,3)(2)h(x)=f(x)-g(x)的零点等价于方程f(x)-g(x)=0的根,
即为函数y=f(x)与y=g(x)图象的交点的横坐标,其大致图象如图,从图象可知它们仅有一个交点A,横坐标的范围为(0,1),故选A.
【答案】 (1)B (2)A【规律总结】判断函数零点所在区间的三种方法
(1)解方程法:当对应方程f(x)=0易解时,可先解方程,然后再看求得的根是否落在给定区间上.
(2)定理法:利用函数零点的存在性定理,首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.
(3)图象法:通过画函数图象,观察图象与x轴在给定区间上是否有交点来判断.变式训练一 A.(0,1) B.(1,2)
C.(2,3) D.(3,4)C 所以x0∈(2,3),故选C. 题型二 函数零点个数的问题 A.3 B.2
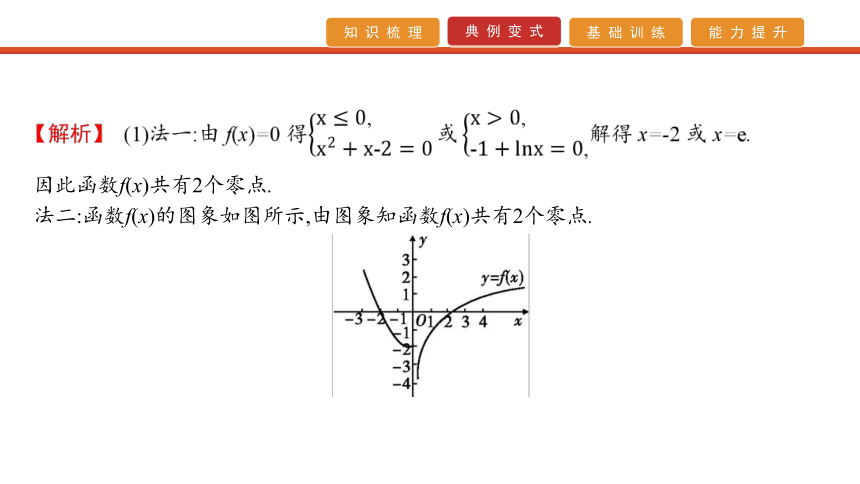
C.1 D.0一个实根,则实数a的取值范围是 .? 因此函数f(x)共有2个零点.
法二:函数f(x)的图象如图所示,由图象知函数f(x)共有2个零点.(2)问题等价于函数y=f(x)与y=-x+a的图象有且只有一个交点,作出函数f(x)的图象(如图所示),结合函数图象可知a>1.【答案】(1)B (2)(1,+∞) 【规律方法】判断函数零点个数的三种方法
(1)方程法:令f(x)=0,如果能求出解,则有几个解就有几个零点.
(2)零点存在性定理法:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质.
(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点. 变式训练二
1.函数f(x)=|x-2|-ln x在定义域内的零点的个数为( )
A.0 B.1 C.2 D.3C 【解析】 由题意可知f(x)的定义域为(0,+∞),在同一直角坐标系中画出函数y1=|x-2|(x>0),y2=ln x(x>0)的图象,如图所示.
由图可知函数f(x)在定义域内的零点个数为2.A.4 B.3 C.2 D.1 A 【解析】 由f(f(x))+1=0得f(f(x))=-1, 综上可得函数y=f(f(x))+1的零点的个数是4,故选A. 题型三 函数零点的应用(高频考点)
函数零点的应用是每年高考的重点,多以选择题或填空题的形式考查,难度中档及以上.主要命题角度有:①已知函数在某区间上有零点求参数;②已知函数零点或方程根的个数求参数.
考法一 根据零点的范围求参数
【例3-1】 若函数f(x)=log2x+x-k(k∈Z)在区间(2,3)上有零点,则k= .?
【解析】 函数f(x)=log2x+x-k在(2,3)上单调递增,所以f(2)·f(3)<0,即(log22+2-k)·
(log23+3-k)<0,整理得(3-k)(log23+3-k)<0,解得3【答案】4考法二 已知函数零点或方程根的个数求参数 数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .?
【解析】 作出f(x)的图象如图所示.当x>m时,x2-2mx+4m=(x-m)2+4m-m2,∴要使方程f(x)=b有三个不同的根,则有4m-m20.又m>0,解得m>3.
【答案】(3,+∞)【规律方法】已知函数的零点或方程根的个数,求参数问题的三种方法
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数的范围.
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,然后数形结合求解.变式训练三 围是 .? (0,1) 【解析】 函数g(x)=f(x)-m有3个零点,转化为f(x)-m=0的根有3个,进而转化为y=f(x),y=m的交点有3个.画出函数y=f(x)的图象,则直线y=m与其有3个公共点.又抛物线顶点为(-1,1),由图可知实数m的取值范围是(0,1).2.设函数f(x)=ex+2x-4,g(x)=ln x+2x2-5,若实数a,b分别是f(x),g(x)的零点,则( )
A.g(a)<0C.00,且函数f(x)是增函数,因此函数f(x)的零点在区间(0,1)内,即00,函数g(x)的零点在区间(1,2)内,即1f(1)>0.又函数g(x)在(0,1)内是增函数,因此有g(a)C.(3,4) D.(4,+∞)A.1 B.2 C.3 D.4 C 故f(x)的零点所在的区间是(3,4). C 个数为3,所以函数f(x)在[0,2π]上的零点个数为3,故选C. 3.已知实数a>1,0A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)4.函数f(x)=2x- -a的一个零点在区间(1,2)内,则实数a的取值范围是( )
A.(1,3) B.(1,2)
C.(0,3) D.(0,2)B 【解析】 因为a>1,00,则由零点存在性定理可知f(x)在区间(-1,0)上存在零点.区间(1,2)内,则有f(1)·f(2)<0,所以(-a)(4-1-a)<0,即a(a-3)<0.所以0A.(-∞,-1) B.(-∞,0)
C.(-1,0) D.[-1,0)D 【解析】 当x>0时,f(x)=3x-1有一个零点x= ,所以只需要当x≤0时,ex+a=0有一个根即可,即ex=-a.当x≤0时,ex∈(0,1],所以-a∈(0,1],即a∈[-1,0).为 .? 3 解①得x=2,解②得x=-1或x=-2,
因此,函数g(x)=f(x)+x的零点个数为3.7.方程2x+3x=k的解在[1,2)内,则k的取值范围为 .? [5,10) 【解析】 令函数f(x)=2x+3x-k,则f(x)在R上是增函数.
当方程2x+3x=k的解在(1,2)内时,f(1)·f(2)<0,即(5-k)(10-k)<0,
解得50)的解的个数是( )
A.1 B.2 C.3 D.4B 【解析】 (数形结合法)因为a>0,所以a2+1>1.
而y=|x2-2x|的图象如图所示,
所以y=|x2-2x|的图象与y=a2+1的图象总有两个交点.2.已知a是函数f(x)=2x- x的零点,若0A.f(x0)=0 B.f(x0)>0
C.f(x0)<0 D.f(x0)的符号不确定C 有零点之和为 .? (1)求g(f(1))的值;
(2)若方程g(f(x))-a=0有4个实数根,求实数a的取值范围.解:(1)利用解析式直接求解得g(f(1))=g(-3)=-3+1=-2.
(2)令f(x)=t,则原方程化为g(t)=a,易知方程f(x)=t在t∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y=g(t)(t<1)与y=a的图象有2个不同的交点,作出函数y=g(t)(t<1)的图象(图略),
(1)函数零点的定义:对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.
(2)三个等价关系:方程f(x)=0有实数根?函数y=f(x)的图象与x轴有交点?函数y=f(x)有零点.
2.函数零点的判定
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是f(x)=0的根.我们把这一结论称为函数零点存在性定理.
3.明确三个等价关系(三者相互转化)4.二次函数y=ax2+bx+c(a>0)的图象与零点的关系 题型一 函数零点所在区间的判断
【例1】 (1)函数f(x)=ln x- 的零点所在的大致区间是( )
A.(1,2) B.(2,3)
C.(1,e)和(3,4) D.(e,+∞)
(2)设f(x)=0.8x-1,g(x)=ln x,则函数h(x)=f(x)-g(x)存在的零点一定位于下列哪个区间( )
A.(0,1) B.(1,2)
C.(2,e) D.(e,3)(2)h(x)=f(x)-g(x)的零点等价于方程f(x)-g(x)=0的根,
即为函数y=f(x)与y=g(x)图象的交点的横坐标,其大致图象如图,从图象可知它们仅有一个交点A,横坐标的范围为(0,1),故选A.
【答案】 (1)B (2)A【规律总结】判断函数零点所在区间的三种方法
(1)解方程法:当对应方程f(x)=0易解时,可先解方程,然后再看求得的根是否落在给定区间上.
(2)定理法:利用函数零点的存在性定理,首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.
(3)图象法:通过画函数图象,观察图象与x轴在给定区间上是否有交点来判断.变式训练一 A.(0,1) B.(1,2)
C.(2,3) D.(3,4)C 所以x0∈(2,3),故选C. 题型二 函数零点个数的问题 A.3 B.2
C.1 D.0一个实根,则实数a的取值范围是 .? 因此函数f(x)共有2个零点.
法二:函数f(x)的图象如图所示,由图象知函数f(x)共有2个零点.(2)问题等价于函数y=f(x)与y=-x+a的图象有且只有一个交点,作出函数f(x)的图象(如图所示),结合函数图象可知a>1.【答案】(1)B (2)(1,+∞) 【规律方法】判断函数零点个数的三种方法
(1)方程法:令f(x)=0,如果能求出解,则有几个解就有几个零点.
(2)零点存在性定理法:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质.
(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点. 变式训练二
1.函数f(x)=|x-2|-ln x在定义域内的零点的个数为( )
A.0 B.1 C.2 D.3C 【解析】 由题意可知f(x)的定义域为(0,+∞),在同一直角坐标系中画出函数y1=|x-2|(x>0),y2=ln x(x>0)的图象,如图所示.
由图可知函数f(x)在定义域内的零点个数为2.A.4 B.3 C.2 D.1 A 【解析】 由f(f(x))+1=0得f(f(x))=-1, 综上可得函数y=f(f(x))+1的零点的个数是4,故选A. 题型三 函数零点的应用(高频考点)
函数零点的应用是每年高考的重点,多以选择题或填空题的形式考查,难度中档及以上.主要命题角度有:①已知函数在某区间上有零点求参数;②已知函数零点或方程根的个数求参数.
考法一 根据零点的范围求参数
【例3-1】 若函数f(x)=log2x+x-k(k∈Z)在区间(2,3)上有零点,则k= .?
【解析】 函数f(x)=log2x+x-k在(2,3)上单调递增,所以f(2)·f(3)<0,即(log22+2-k)·
(log23+3-k)<0,整理得(3-k)(log23+3-k)<0,解得3
【解析】 作出f(x)的图象如图所示.当x>m时,x2-2mx+4m=(x-m)2+4m-m2,∴要使方程f(x)=b有三个不同的根,则有4m-m2
【答案】(3,+∞)【规律方法】已知函数的零点或方程根的个数,求参数问题的三种方法
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数的范围.
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,然后数形结合求解.变式训练三 围是 .? (0,1) 【解析】 函数g(x)=f(x)-m有3个零点,转化为f(x)-m=0的根有3个,进而转化为y=f(x),y=m的交点有3个.画出函数y=f(x)的图象,则直线y=m与其有3个公共点.又抛物线顶点为(-1,1),由图可知实数m的取值范围是(0,1).2.设函数f(x)=ex+2x-4,g(x)=ln x+2x2-5,若实数a,b分别是f(x),g(x)的零点,则( )
A.g(a)<0
C.(0,1) D.(1,2)4.函数f(x)=2x- -a的一个零点在区间(1,2)内,则实数a的取值范围是( )
A.(1,3) B.(1,2)
C.(0,3) D.(0,2)B 【解析】 因为a>1,0
C.(-1,0) D.[-1,0)D 【解析】 当x>0时,f(x)=3x-1有一个零点x= ,所以只需要当x≤0时,ex+a=0有一个根即可,即ex=-a.当x≤0时,ex∈(0,1],所以-a∈(0,1],即a∈[-1,0).为 .? 3 解①得x=2,解②得x=-1或x=-2,
因此,函数g(x)=f(x)+x的零点个数为3.7.方程2x+3x=k的解在[1,2)内,则k的取值范围为 .? [5,10) 【解析】 令函数f(x)=2x+3x-k,则f(x)在R上是增函数.
当方程2x+3x=k的解在(1,2)内时,f(1)·f(2)<0,即(5-k)(10-k)<0,
解得5
A.1 B.2 C.3 D.4B 【解析】 (数形结合法)因为a>0,所以a2+1>1.
而y=|x2-2x|的图象如图所示,
所以y=|x2-2x|的图象与y=a2+1的图象总有两个交点.2.已知a是函数f(x)=2x- x的零点,若0
C.f(x0)<0 D.f(x0)的符号不确定C 有零点之和为 .? (1)求g(f(1))的值;
(2)若方程g(f(x))-a=0有4个实数根,求实数a的取值范围.解:(1)利用解析式直接求解得g(f(1))=g(-3)=-3+1=-2.
(2)令f(x)=t,则原方程化为g(t)=a,易知方程f(x)=t在t∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y=g(t)(t<1)与y=a的图象有2个不同的交点,作出函数y=g(t)(t<1)的图象(图略),
同课章节目录
