2020版高考艺考生文化课百日冲刺 第16讲 指数函数、对数函数、二次函数、幂函数(课件:54张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第16讲 指数函数、对数函数、二次函数、幂函数(课件:54张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览







文档简介
课件54张PPT。第16讲 指数函数、对数函数、二次函数、幂函数1.幂函数
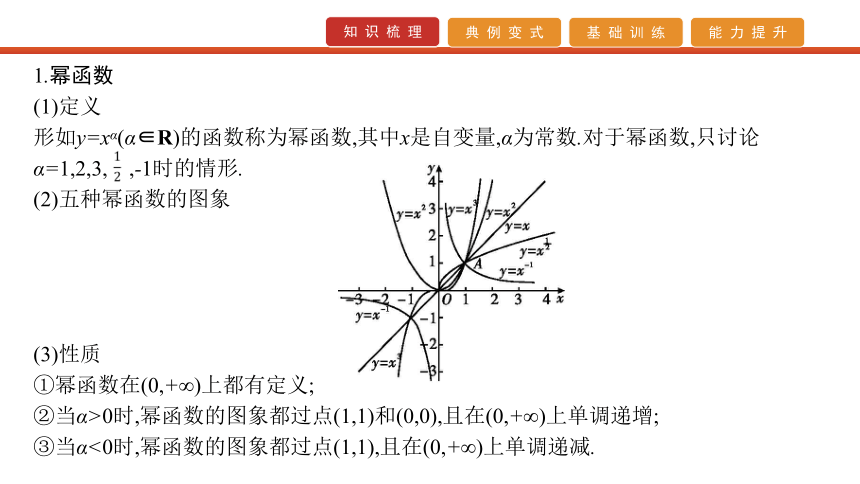
(1)定义
形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α为常数.对于幂函数,只讨论α=1,2,3, ,-1时的情形.
(2)五种幂函数的图象
(3)性质
①幂函数在(0,+∞)上都有定义;
②当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增;
③当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减.2.二次函数
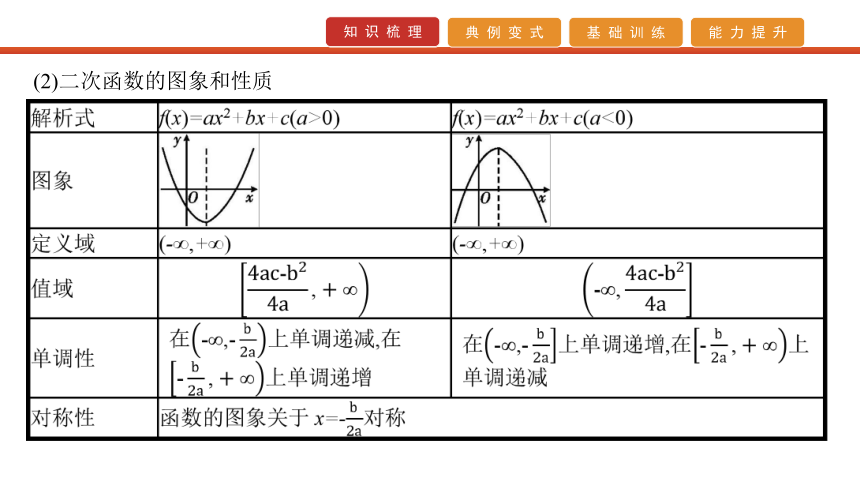
(1)二次函数解析式的三种形式顶点式:f(x)=a(x-m)2+n(a≠0),图象的对称轴是x=m,顶点坐标是(m,n);
零点式:f(x)=a(x-x1)(x-x2)(a≠0),其中x1,x2是方程ax2+bx+c=0的两根,图象的对称轴是(2)二次函数的图象和性质 3.根式
(1)根式的概念
若xn=a,则x叫做a的n次方根,其中n>1且n∈N*.式子 叫做根式,这里n叫做根指数,a叫做被开方数.
(2)a的n次方根的表示(2)根式的性质 4.有理数指数幂
(1)幂的有关概念③0的正分数指数幂等于0,0的负分数指数幂无意义.
(2)有理数指数幂的运算性质
①aras=ar+s(a>0,r,s∈Q);
②(ar)s=ars(a>0,r,s∈Q);
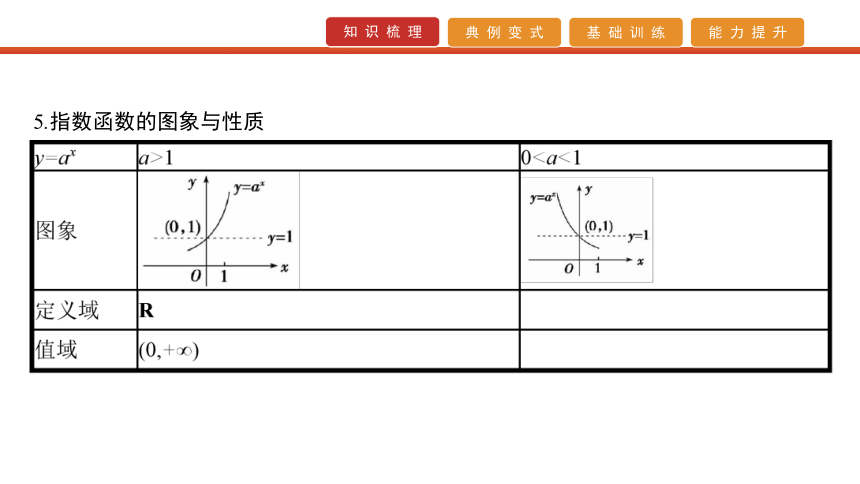
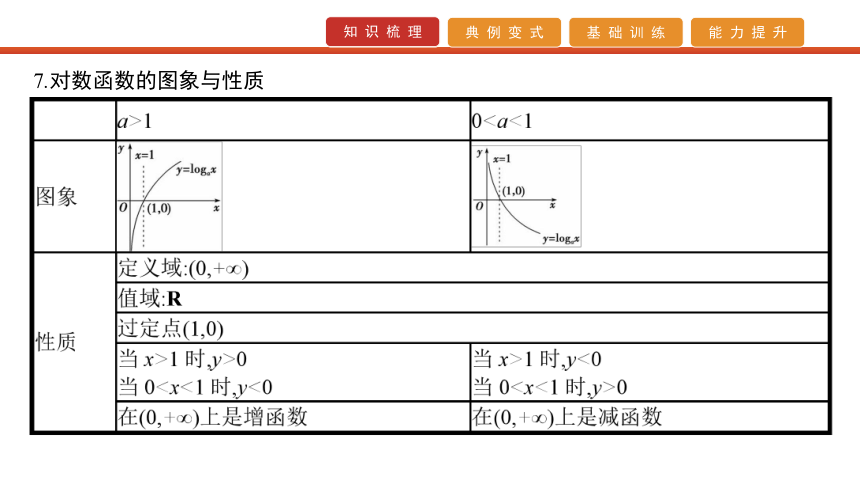
③(ab)r=arbr(a>0,b>0,r∈Q).5.指数函数的图象与性质 6.对数 7.对数函数的图象与性质 8.反函数
指数函数y=ax与对数函数y=logax互为反函数,它们的图象关于直线y=x对称.题型一 幂函数的图象及性质 A.aC.b(1)对于幂函数图象的掌握只要抓住在第一象限内三条线分第一象限为六个区域,即x=1,y=1,y=x所分区域.根据α<0,0<α<1,α=1,α>1的取值确定位置后,其余象限部分由奇偶性决定.
(2)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较.变式训练一 C图象在第一象限为上凸的,排除D,故选C. A.-3 B.1 C.2 D.1或2 B 【解析】 由于f(x)为幂函数,所以n2+2n-2=1,解得n=1或n=-3.当n=1时,f(x)=x-2= 在(0,+∞)上是减函数;当n=-3时,f(x)=x18在(0,+∞)上是增函数.故n=1符合题意,应选B.题型二 二次函数的图象与性质
高考对二次函数图象与性质进行考查,多与其他知识结合,且常以选择题形式出现,难度为中高档题.
高考对二次函数图象与性质的考查主要从以下三个角度命题:①二次函数图象的识别问题;②二次函数的最值问题;③一元二次不等式恒成立问题.【例2】 (1)已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,则实数a的值为 .?
(2)已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是 .?
【解析】 (1)f(x)=-(x-a)2+a2-a+1,
当a≥1时,ymax=a;
当0当a≤0时,ymax=1-a.
根据已知条件得,解得a=2或a=-1. (2)作出二次函数f(x)的图象,对于任意x∈[m,m+1],都有f(x)<0,则有 【规律方法】
(1)二次函数最值问题的类型及处理思路:①类型:a.对称轴、区间都是给定的;b.对称轴动、区间固定;c.对称轴定、区间变动.②解决这类问题的思路:抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合配方法,根据函数的单调性及分类讨论的思想即可完成.
(2)二次函数中恒成立问题的求解思路:①一般有两个解题思路:一是分离参数;二是不分离参数.②两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否已分离.这两个思路的依据是:a≥f(x)?a≥f(x)max,a≤f(x)?a≤f(x)min.变式训练二
1.已知函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象是( )D 【解析】 因为a>b>c,且a+b+c=0,得a>0,且c<0,所以f(0)=c<0,所以函数y=ax2+bx+c的图象开口向上,与y轴的交点在y轴的负半轴上.2.设函数y=x2-2x,x∈[-2,a],若函数的最小值为0,则a= .? 0 【解析】 因为函数y=x2-2x=(x-1)2-1,所以对称轴为直线x=1,
因为x=1不一定在区间[-2,a]内,所以应进行讨论.
当-2所以a2-2a=0,所以a=0,a=2(舍去),
当a>1时,函数在[-2,1]上单调递减,在[1,a]上单调递增,则当x=1时,y取得最小值,
即ymin=-1.不合题意.
故a的值为0.3.已知f(x)=x2+2(a-2)x+4,如果对x∈[-3,1],f(x)>0恒成立,则实数a的取值范围为 .?【解析】 因为f(x)=x2+2(a-2)x+4,
对称轴x=-(a-2),对x∈[-3,1],f(x)>0恒成立,题型三 指数与对数运算 【规律方法】 【注意】运算结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数,形式力求统一。【注意】在运算中要注意对数化同底和指数与对数的互化。 变式训练三
1.化简:2.(1)lg 25+lg 2·lg 50+(lg 2)2= .? 【解析】 (1)原式=(lg 2)2+(1+lg 5)lg 2+lg 52=(lg 2+lg 5+1)lg 2+2lg 5
=2lg 2+2lg 5=2(lg 2+lg 5)=2.A 【解析】∵2a=5b=m,
∴a=log2m,b=log5m,题型四 指数与对数不等式 b=f(log24.1),c=f(20.8),则a,b,c的大小关系为( )
A.aC.c(2)设a,b都是不等于1的正数,则“3a>3b>3”是“loga3A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件因为log25>log24.1>log24=2>20.8,且函数f(x)是增函数,所以c(2)“3a>3b>3”等价于“a>b>1”,“loga3b>1或03b>3”是“loga3【答案】 (1)C (2) B
【规律方法】指数函数的图象及应用
(1)与指数函数有关的函数图象的研究,往往利用相应指数函数的图象,通过平移、对称、翻折变换得到其图象.
(2)一些指数型方程、不等式问题的求解,往往利用相应的指数型函数图象数形结合求解.【注意】利用对数函数的图象可求解的两类热点问题:①对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想求解.②一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.变式训练四 A.a>1,b<0 B.a>1,b>0
C.00 D.00,a≠1)的图象如图所示,则a、b满足的关系式( )
A.0C.01,函数图象与y轴的交点坐标为(0,logab),A.aC.c(1)比较指数幂大小问题,常利用指数函数的单调性及中间值(0或1).
(2)求解简单的指数不等式问题,应利用指数函数的单调性,要特别注意底数a的取值范围,并在必要时进行分类讨论.
(3)求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归结为内层函数相关的问题加以解决.
【注意】在研究指数型函数单调性时,当底数与“1”的大小关系不明确时,要分类讨论.【规律方法】有关对数函数性质的问题类型及解题策略
(1)对对数函数性质的考查主要从以下四个角度命题:
①求对数函数的定义域;②解简单的对数不等式或方程;③比较对数值的大小;④探究对数函数的性质.
(2)利用对数函数的性质,求与对数函数有关的函数的值域和单调性问题时,必须弄清三方面的问题:一是定义域,所有问题都必须在定义域内讨论;二是底数与1的大小关系;三是函数的构成形式,即它是由哪些基本初等函数通过初等运算构成或复合而成的.变式训练五
1.设a=log32,b=log52,c=log23,则( )
A.a>c>b B.b>c>a
C.c>b>a D.c>a>bD ∴c>a>b. 2.若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上递减,则a的取值范围是( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)A【解析】 令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,对称轴为x=a,要使函数在(-∞,1]上 方程f(x)=0有实根?函数y=f(x)的图象与x轴有公共点?函数y=f(x)有零点. 1.幂函数y=f(x)的图象经过点(3, ),则f(x)是( )
A.偶函数,且在(0,+∞)上是增函数
B.偶函数,且在(0,+∞)上是减函数
C.奇函数,且在(0,+∞)上是减函数
D.非奇非偶函数,且在(0,+∞)上是增函数D 且在(0,+∞)上是增函数.故选D. 2.已知函数f(x)=x2+(a+1)x+ab,若不等式f(x)≤0的解集为{x|-1≤x≤4},则a+2b的值为( )
A.-2 B.3 C.-3 D.2A 3.(2018·南昌一模)已知函数f(x)=x2+ax+b的图象过坐标原点,且满足f(-x)=f(-1+x),则函数f(x)在[-1,3]上的值域为( )B 【解析】 因为函数f(x)=x2+ax+b的图象过坐标原点,所以f(0)=0,所以b=0.因为f(-x)A.bC.bC.[-2,+∞) D.(-∞,-2]A 指数函数y=16x在R上单调递增,所以b0,且a≠1)的图象如图所示,则下列函数图象正确的是( ) B 【解析】 由题意y=logax(a>0,且a≠1)的图象过(3,1)点,可解得a=3.选项A中,y=3-x
= ,显然图象错误;选项B中,y=x3,由幂函数图象可知正确;选项C中,y=(-x)3=-x3,显然与所画图象不符;选项D中,y=log3(-x)的图象与y=log3x的图象关于y轴对称,显然不符.故选B.8.已知函数f(x)=x2-2ax+2a+4的定义域为R,值域为[1,+∞),则a的值为 .?-1或3 【解析】 由于函数f(x)的值域为[1,+∞),
所以f(x)min=1.
又f(x)=(x-a)2-a2+2a+4,
当x∈R时,f(x)min=f(a)=-a2+2a+4=1,
即a2-2a-3=0,
解得a=3或a=-1.9.当x∈(-∞,-1]时,不等式(m2-m)·4x-2x<0恒成立,则实数m的取值范围是 .?(-1,2) 为 .? D 2.已知函数f(x)=|2x-1|,af(c)>f(b),则下列结论中,一定成立的是( )
A.a<0,b<0,c<0 B.a<0,b≥0,c>0
C. <2c D.2a+2c<2D 【解析】 作出函数f(x)=|2x-1|的图象,如图,
因为af(c)>f(b),
结合图象知,00,
所以0<2a<1.
所以f(a)=|2a-1|=1-2a<1,
所以f(c)<1,所以0所以1<2c<2,所以f(c)=|2c-1|=2c-1,
又因为f(a)>f(c),
所以1-2a>2c-1,
所以2a+2c<2,故选D.3.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若
f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为 .?【解析】 由题意知,y=f(x)-g(x)=x2-5x+4-m在[0,3]上有两个不同的零点.在同一直角坐标系下作出函数y=m与y=x2-5x+4(x∈[0,3])的图象如图所示,结合图象可知,当x∈[2,3]时,交点. 4.设函数f(x)=|logax|(0实数a的值为 .?【解析】 作出y=|logax|(0
(1)定义
形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α为常数.对于幂函数,只讨论α=1,2,3, ,-1时的情形.
(2)五种幂函数的图象
(3)性质
①幂函数在(0,+∞)上都有定义;
②当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增;
③当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减.2.二次函数
(1)二次函数解析式的三种形式顶点式:f(x)=a(x-m)2+n(a≠0),图象的对称轴是x=m,顶点坐标是(m,n);
零点式:f(x)=a(x-x1)(x-x2)(a≠0),其中x1,x2是方程ax2+bx+c=0的两根,图象的对称轴是(2)二次函数的图象和性质 3.根式
(1)根式的概念
若xn=a,则x叫做a的n次方根,其中n>1且n∈N*.式子 叫做根式,这里n叫做根指数,a叫做被开方数.
(2)a的n次方根的表示(2)根式的性质 4.有理数指数幂
(1)幂的有关概念③0的正分数指数幂等于0,0的负分数指数幂无意义.
(2)有理数指数幂的运算性质
①aras=ar+s(a>0,r,s∈Q);
②(ar)s=ars(a>0,r,s∈Q);
③(ab)r=arbr(a>0,b>0,r∈Q).5.指数函数的图象与性质 6.对数 7.对数函数的图象与性质 8.反函数
指数函数y=ax与对数函数y=logax互为反函数,它们的图象关于直线y=x对称.题型一 幂函数的图象及性质 A.a
(2)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较.变式训练一 C图象在第一象限为上凸的,排除D,故选C. A.-3 B.1 C.2 D.1或2 B 【解析】 由于f(x)为幂函数,所以n2+2n-2=1,解得n=1或n=-3.当n=1时,f(x)=x-2= 在(0,+∞)上是减函数;当n=-3时,f(x)=x18在(0,+∞)上是增函数.故n=1符合题意,应选B.题型二 二次函数的图象与性质
高考对二次函数图象与性质进行考查,多与其他知识结合,且常以选择题形式出现,难度为中高档题.
高考对二次函数图象与性质的考查主要从以下三个角度命题:①二次函数图象的识别问题;②二次函数的最值问题;③一元二次不等式恒成立问题.【例2】 (1)已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,则实数a的值为 .?
(2)已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是 .?
【解析】 (1)f(x)=-(x-a)2+a2-a+1,
当a≥1时,ymax=a;
当0
根据已知条件得,解得a=2或a=-1. (2)作出二次函数f(x)的图象,对于任意x∈[m,m+1],都有f(x)<0,则有 【规律方法】
(1)二次函数最值问题的类型及处理思路:①类型:a.对称轴、区间都是给定的;b.对称轴动、区间固定;c.对称轴定、区间变动.②解决这类问题的思路:抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合配方法,根据函数的单调性及分类讨论的思想即可完成.
(2)二次函数中恒成立问题的求解思路:①一般有两个解题思路:一是分离参数;二是不分离参数.②两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否已分离.这两个思路的依据是:a≥f(x)?a≥f(x)max,a≤f(x)?a≤f(x)min.变式训练二
1.已知函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象是( )D 【解析】 因为a>b>c,且a+b+c=0,得a>0,且c<0,所以f(0)=c<0,所以函数y=ax2+bx+c的图象开口向上,与y轴的交点在y轴的负半轴上.2.设函数y=x2-2x,x∈[-2,a],若函数的最小值为0,则a= .? 0 【解析】 因为函数y=x2-2x=(x-1)2-1,所以对称轴为直线x=1,
因为x=1不一定在区间[-2,a]内,所以应进行讨论.
当-2
当a>1时,函数在[-2,1]上单调递减,在[1,a]上单调递增,则当x=1时,y取得最小值,
即ymin=-1.不合题意.
故a的值为0.3.已知f(x)=x2+2(a-2)x+4,如果对x∈[-3,1],f(x)>0恒成立,则实数a的取值范围为 .?【解析】 因为f(x)=x2+2(a-2)x+4,
对称轴x=-(a-2),对x∈[-3,1],f(x)>0恒成立,题型三 指数与对数运算 【规律方法】 【注意】运算结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数,形式力求统一。【注意】在运算中要注意对数化同底和指数与对数的互化。 变式训练三
1.化简:2.(1)lg 25+lg 2·lg 50+(lg 2)2= .? 【解析】 (1)原式=(lg 2)2+(1+lg 5)lg 2+lg 52=(lg 2+lg 5+1)lg 2+2lg 5
=2lg 2+2lg 5=2(lg 2+lg 5)=2.A 【解析】∵2a=5b=m,
∴a=log2m,b=log5m,题型四 指数与对数不等式 b=f(log24.1),c=f(20.8),则a,b,c的大小关系为( )
A.a
C.必要不充分条件 D.既不充分也不必要条件因为log25>log24.1>log24=2>20.8,且函数f(x)是增函数,所以c
【规律方法】指数函数的图象及应用
(1)与指数函数有关的函数图象的研究,往往利用相应指数函数的图象,通过平移、对称、翻折变换得到其图象.
(2)一些指数型方程、不等式问题的求解,往往利用相应的指数型函数图象数形结合求解.【注意】利用对数函数的图象可求解的两类热点问题:①对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想求解.②一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.变式训练四 A.a>1,b<0 B.a>1,b>0
C.0
A.0
(2)求解简单的指数不等式问题,应利用指数函数的单调性,要特别注意底数a的取值范围,并在必要时进行分类讨论.
(3)求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归结为内层函数相关的问题加以解决.
【注意】在研究指数型函数单调性时,当底数与“1”的大小关系不明确时,要分类讨论.【规律方法】有关对数函数性质的问题类型及解题策略
(1)对对数函数性质的考查主要从以下四个角度命题:
①求对数函数的定义域;②解简单的对数不等式或方程;③比较对数值的大小;④探究对数函数的性质.
(2)利用对数函数的性质,求与对数函数有关的函数的值域和单调性问题时,必须弄清三方面的问题:一是定义域,所有问题都必须在定义域内讨论;二是底数与1的大小关系;三是函数的构成形式,即它是由哪些基本初等函数通过初等运算构成或复合而成的.变式训练五
1.设a=log32,b=log52,c=log23,则( )
A.a>c>b B.b>c>a
C.c>b>a D.c>a>bD ∴c>a>b. 2.若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上递减,则a的取值范围是( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)A【解析】 令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,对称轴为x=a,要使函数在(-∞,1]上 方程f(x)=0有实根?函数y=f(x)的图象与x轴有公共点?函数y=f(x)有零点. 1.幂函数y=f(x)的图象经过点(3, ),则f(x)是( )
A.偶函数,且在(0,+∞)上是增函数
B.偶函数,且在(0,+∞)上是减函数
C.奇函数,且在(0,+∞)上是减函数
D.非奇非偶函数,且在(0,+∞)上是增函数D 且在(0,+∞)上是增函数.故选D. 2.已知函数f(x)=x2+(a+1)x+ab,若不等式f(x)≤0的解集为{x|-1≤x≤4},则a+2b的值为( )
A.-2 B.3 C.-3 D.2A 3.(2018·南昌一模)已知函数f(x)=x2+ax+b的图象过坐标原点,且满足f(-x)=f(-1+x),则函数f(x)在[-1,3]上的值域为( )B 【解析】 因为函数f(x)=x2+ax+b的图象过坐标原点,所以f(0)=0,所以b=0.因为f(-x)A.b
= ,显然图象错误;选项B中,y=x3,由幂函数图象可知正确;选项C中,y=(-x)3=-x3,显然与所画图象不符;选项D中,y=log3(-x)的图象与y=log3x的图象关于y轴对称,显然不符.故选B.8.已知函数f(x)=x2-2ax+2a+4的定义域为R,值域为[1,+∞),则a的值为 .?-1或3 【解析】 由于函数f(x)的值域为[1,+∞),
所以f(x)min=1.
又f(x)=(x-a)2-a2+2a+4,
当x∈R时,f(x)min=f(a)=-a2+2a+4=1,
即a2-2a-3=0,
解得a=3或a=-1.9.当x∈(-∞,-1]时,不等式(m2-m)·4x-2x<0恒成立,则实数m的取值范围是 .?(-1,2) 为 .? D 2.已知函数f(x)=|2x-1|,a
A.a<0,b<0,c<0 B.a<0,b≥0,c>0
C. <2c D.2a+2c<2D 【解析】 作出函数f(x)=|2x-1|的图象,如图,
因为a
结合图象知,0
所以0<2a<1.
所以f(a)=|2a-1|=1-2a<1,
所以f(c)<1,所以0
又因为f(a)>f(c),
所以1-2a>2c-1,
所以2a+2c<2,故选D.3.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若
f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为 .?【解析】 由题意知,y=f(x)-g(x)=x2-5x+4-m在[0,3]上有两个不同的零点.在同一直角坐标系下作出函数y=m与y=x2-5x+4(x∈[0,3])的图象如图所示,结合图象可知,当x∈[2,3]时,交点. 4.设函数f(x)=|logax|(0
同课章节目录
