2020版高考艺考生文化课百日冲刺 第15讲 函数与函数图象及性质(课件:61张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第15讲 函数与函数图象及性质(课件:61张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览










文档简介
课件61张PPT。第15讲 函数与函数图象及性质1.函数的有关概念
(1)函数的定义域、值域:在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.显然,值域是集合B的子集.
(2)函数的三要素:定义域、值域和对应关系.
(3)相等函数:如果两个函数的定义域和对应关系完全一致,则这两个函数相等,这是判断两函数相等的依据.
2.分段函数
若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数.
3.分段函数的相关结论
(1)分段函数虽由几个部分组成,但它表示的是一个函数.
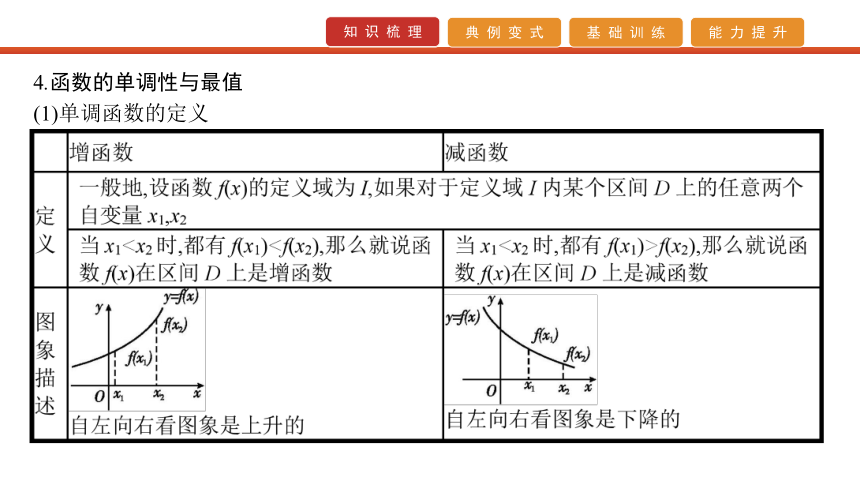
(2)分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数的值域的并集.4.函数的单调性与最值
(1)单调函数的定义(2)单调区间的定义
若函数y=f(x)在区间D上是增函数或减函数,则称函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.
(3)函数的最值(4)函数最值存在的两条结论
(1)闭区间上的连续函数一定存在最大值和最小值.当函数在闭区间上单调时最值一定在端点处取到.
(2)开区间上的“单峰”函数一定存在最大或最小值.5.函数的奇偶性与周期
(1)定义(2)函数奇偶性常用结论
如果函数f(x)是偶函数,那么f(x)=f(|x|).
奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.
在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.(3)周期函数
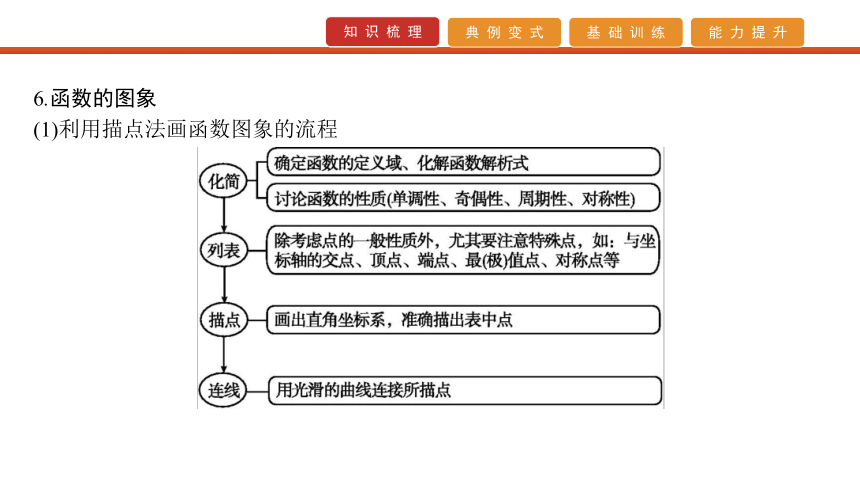
对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有f(x+T)=f(x),那么就称函数y=f(x)为周期函数,称T为这个函数的周期.6.函数的图象
(1)利用描点法画函数图象的流程(2)利用图象变换法作函数的图象
平移变换:伸缩变换: 对称变换: 翻折变换: 题型一 求函数定义域 A.(-3,0] B.(-3,1]
C.(-∞,-3)∪(-3,0] D.(-∞,-3)∪(-3,1]A.(-1,+∞) B.[-1,+∞)
C.(-1,1)∪(1,+∞) D.[-1,1)∪(1,+∞)【答案】 (1)A (2)C
【规律方法】【易错警示】求定义域时,对解析式不要化简,求出定义域后一定要将其写成集合或区间形式.
【注意】不要对解析式进行化简变形,以免定义域发生变化.变式训练一 A.(-4,-1) B.(-4,1)
C.(-1,1) D.(-1,1]C x∈(0,1] 3.(1)已知函数f(x)的定义域为(0,1),求f(x2)的定义域;
(2)已知函数f(x2)的定义域为(2,4),求f(x)的定义域;
(3)已知函数f(x2)的定义域为(1,2),求f(2x+1)的定义域.解:(1)f(x)的定义域为(0,1),即0∴-1(2)f(x2)的定义域为(2,4),即2故f(x)的定义域为(4,16).
(3)∵f(x2)的定义域为(1,2),即1则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+5a+b
即ax+5a+b=2x+17,不论x为何值都成立.【规律方法】求函数解析式的常用方法
(1)待定系数法:若已知函数的类型,可用待定系数法;
(2)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;式,通过解方程组求出f(x);
(4)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),即得f(x)的表达式.变式训练二 f(x)=x2-2(x≥2或x≤-2) ∴f(x)=x2-2(x≥2或x≤-2). 题型三 函数的单调性 (2)(2019·青岛模拟)已知函数f(x)=x3+sinx,x∈(-1,1),则满足f(a2-1)+f(a-1)>0的a的取值范围是( )(3)若函数f(x)=ax2+2x-3在区间(-∞,4)上是单调递增的,则实数a的取值范围是( ) (2)由题意知f(-x)=(-x)3+sin(-x)=-x3-sinx=-(x3+sinx)=-f(x),x∈(-1,1),
∴f(x)在区间(-1,1)上是奇函数.
又f'(x)=3x2+cosx>0,
∴f(x)在区间(-1,1)上单调递增,
∵f(a2-1)+f(a-1)>0,
∴-f(a-1)∴f(1-a)【答案】(1)B (2)B (3)D (4)(2,3]【规律方法】
(1)判断函数单调性的常用方法(2)确定函数的单调区间的方法 变式训练三 C【解析】当x=1时,loga1=0,若f(x)为R上的减函数,则(3a-1)x+4a≥0在x<1时恒成立.
令g(x)=(3a-1)x+4a.值范围是( )
A.(-∞,1] B.[1,4]
C.[4,+∞) D.(-∞,1]∪[4,+∞)D 【解析】作出f(x)的图象如图,由图象可知f(x)的单调递增区间是(-∞,2]和(4,+∞),
∵函数y=f(x)在(a,a+1)上单调递增,需满足a≥4或a+1≤2,即a≤1或a≥4.故选D.题型四 函数的奇偶性、对称性及周期性
【例4-1】 (1)判断下列函数的奇偶性.∴f(x)的定义域为{-1,1}.
又f(1)+f(-1)=0,f(1)-f(-1)=0,
∴f(x)=±f(-x).
∴f(x)既是奇函数又是偶函数.
④易知函数的定义域为(-∞,0)∪(0,+∞),关于原点对称,又当x>0时,f(x)=x2+x,
则当x<0时,-x>0,
故f(-x)=x2-x=f(x);
当x<0时,f(x)=x2-x,则当x>0时,-x<0,
故f(-x)=x2+x=f(x),故原函数是偶函数.(3)∵f(x)是定义在R上的奇函数,∴f(0)=0.
又当x<0时,-x>0,∴f(-x)=x2+4x.又f(x)为奇函数,
∴f(-x)=-f(x),
即f(x)=-x2-4x(x<0),(4)由题意,得f(-1)+f(1)=0,即2(a+1)=0,解得a=-1,经检验,a=-1时,函数f(x)为奇函数.
【答案】(1)①奇函数 ②奇函数 ③既奇又偶函数 ④偶函数 (2)-2 【例4-2】 (1)(2019·沈阳模拟)已知函数f(x)满足f(x+1)=-f(x),且当0≤x≤1时, f(1)+f(2)+f(3)+…+f(2018)的值为 .? 【解析】 (1)由f(x+1)=-f(x)得f(x+2)=-f(x+1)=f(x),即函数f(x)的周期为2, ∴f(1)+f(2)+f(3)+…+f(2018)
=504[f(1)+f(2)+f(3)+f(4)]+f(504×4+1)+f(504×4+2)=1348.
【答案】(1)A (2)A (3)1348【规律方法】
(1)判断函数周期性的方法
①定义法:判断函数的周期性只需证明f(x+T)=f(x)(T≠0)便可证明函数是周期函数,且周期为T.
②结论法:对f(x)定义域内任一自变量的值x,
ⅰ.若f(x+a)=-f(x),则T=2a(a>0);(2)函数周期性的应用,根据函数的周期性,可以由函数局部的性质得到函数的整体性质,即周期性可将未知区间上的函数值、解析式、图象转化到已知区间上,在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期.变式训练四
1.已知函数f(x)=x3+sin x+1(x∈R),若f(a)=2,则f(-a)的值为( )
A.3 B.0
C.-1 D.-2A.-1 B.-2
C.1 D.2B 【解析】 设F(x)=f(x)-1=x3+sin x,显然F(x)为奇函数,又F(a)=f(a)-1=1,所以F(-a)=f(-a)-1=-1,从而f(-a)=0.故选B.A 【解析】 因为f(x)为奇函数,所以f(-8)=-f(8)=-log39=-2,
所以g[f(-8)]=g(-2)=f(-2)=-f(2)=-log33=-1.3.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(1+x),则x<0时,f(x)= .?则下列函数值为1的是( )
A.f(2.5) B.f(f(2.5))
C.f(f(1.5)) D.f(2)x(1-x) 【解析】 当x<0时,则-x>0,
所以f(-x)=(-x)(1-x).又f(x)为奇函数,
所以f(-x)=-f(x)=(-x)(1-x),所以f(x)=x(1-x).D【解析】 由f(x+1)=-f(x)知f(x+2)=-f(x+1)=f(x),于是f(x)是以2为周期的周期函数,从而f(2.5)=f(0.5)=-1,f(f(2.5))=f(-1)=f(1)=-1,f(f(1.5))=f(f(-0.5))=f(1)=-1,f(2)=f(0)=1,故选D.5.设定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+f(3)+…+f(2019)= .?1010 【解析】 ∵f(x+2)=f(x),
∴函数f(x)的周期T=2.
又当x∈[0,2)时,f(x)=2x-x2,∴f(0)=0,f(1)=1,f(0)+f(1)=1.
∴f(0)+f(1)=f(2)+f(3)=f(4)+f(5)=…=f(2018)+f(2019)=1,
∴f(0)+f(1)+f(2)+…+f(2019)=1010.题型五 作函数图像
【例5】 作出下列函数的图象:(2)将函数y=log2x的图象向左平移1个单位,再将x轴下方的部分沿x轴翻折上去,即可得到函数y=|log2(x+1)|的图象,如图.先用描点法作出[0,+∞)上的图象,再根据对称性作出(-∞,0)上的图象,即得函数图象如图.【规律方法】函数图象的画法 变式训练五
作下列函数的图象:(2)y=x2-2x+2,x∈(-1,2];
(3)y=|x-1|,x∈R.(2)用描点法作出函数f(x)=x2-2x+2,x∈(-1,2]的图象,如图②所示. (3)可先作出y=x-1的图象,将x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变可得y=|x-1|的图象.如图③中实线部分所示.题型六 函数图象的识别
【例6】 (1)函数y=(x3-x)2|x|的图象大致是( ) A B C D (2)如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( ) A B C D 【解析】 (1)易判断函数为奇函数,由y=0得x=±1或x=0.且当01时,y>0,故选B.
(2)法一:由题意可知点P的轨迹为图中虚线所示,其中四个角均是半径为 的扇形.
因为矩形ABCD的周长为8,AB=x,【答案】 (1)B (2)D 【规律方法】识辨函数图象的入手点
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势.
(3)从函数的奇偶性,判断图象的对称性.
(4)从函数的周期性,判断图象的循环往复.
(5)从函数的特征点,排除不合要求的图象.变式训练六 A B C D A B B 【解析】 由定义知,当x≥0时,2x≥1,∴f(x)=2x,当x<0时,2x<1,∴f(x)=1, 4.如图,不规则四边形ABCD中,AB和CD是线段,AD和BC是圆弧,直线l⊥AB交AB于点E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,左侧部分的面积为y,则y关于x的图象大致是( )C 【解析】 当l从左至右移动时,一开始面积的增加速度越来越快,过了D点后面积保持匀速增加,图象呈直线变化,过了C点后面积的增加速度又逐渐减慢.故选C.1.若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是( )B 【解析】 可以根据函数的概念进行排除,使用筛选法得到答案. B 3.设函数f(x)=2x+3,g(x+2)=f(x),则g(x)的表达式是( )
A.g(x)=2x+1 B.g(x)=2x-1
C.g(x)=2x-3 D.g(x)=2x+7B 【解析】 令t=x+2?x=t-2,则有g(x+2)=f(x)?g(t)=f(t-2)=2(t-2)+3=2t-1. D5.(2019·开封模拟)已知f(x)是定义在R上周期为4的奇函数,当x∈(0,2]时,f(x)=2x+log2x,则f(2019)=( )
A.5 B.
C.2 D.-2D 【解析】 由题意得f(2019)=f(4×505-1)=f(-1)=-f(1)=-(21+log21)=-2,故选D. 6.下列四个函数中,在区间(0,1)上是减函数的是( ) D (0,1)上是单调递增的,故排除. 7.若函数f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是( )
A.(-1,0) B.(-1,0)∪(0,1]
C.(0,1) D.(0,1]A.cC.bA.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0B 10.y=-x2+2|x|+3的单调增区间为 .? (-∞,-1],[0,1] 由图象可以得知,函数y=-x2+2|x|+3的单调增区间为(-∞,-1],[0,1] 1.定义在R上的偶函数f(x),对任意x1,x2∈[0,+∞),(x1≠x2),有 <0,则( )
A.f(3)C.f(-2)又f(x)是偶函数,故f(x)在x1,x2∈(0,+∞](x1≠x2)单调递减.
且满足n∈N*时,f(-2)=f(2),3>2>1>0,得f(1)>f(-2)>f(3).2.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )
A.-3 B.-1
C.1 D.3C 【解析】∵f(x)-g(x)=x3+x2+1,∴f(-1)-g(-1)=-1+1+1=1,又∵f(x),g(x)分别是定义在R上的偶函数和奇函数,∴f(1)=f(-1),g(1)=-g(-1),∴f(-1)-g(-1)=f(1)+g(1),∴f(1)+g(1)=1.3.已知f(x)是定义在R上的奇函数,且在[0,+∞)单调递增,若f(lg x)<0,则x的取值范围是( )
A.(0,1) B.(1,10) C.(1,+∞) D.(10,+∞)A 【解析】由f(x)在定义域R上为奇函数知f(0)=0且函数图象关于原点O对称.结合f(x)在[0,+∞)上递增可知,函数在(0,+∞)上恒为正,在(-∞,0)上递增且恒为负.因为f(lgx)<0,所以lgx<0,解得x∈(0,1).
(1)函数的定义域、值域:在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.显然,值域是集合B的子集.
(2)函数的三要素:定义域、值域和对应关系.
(3)相等函数:如果两个函数的定义域和对应关系完全一致,则这两个函数相等,这是判断两函数相等的依据.
2.分段函数
若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数.
3.分段函数的相关结论
(1)分段函数虽由几个部分组成,但它表示的是一个函数.
(2)分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数的值域的并集.4.函数的单调性与最值
(1)单调函数的定义(2)单调区间的定义
若函数y=f(x)在区间D上是增函数或减函数,则称函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.
(3)函数的最值(4)函数最值存在的两条结论
(1)闭区间上的连续函数一定存在最大值和最小值.当函数在闭区间上单调时最值一定在端点处取到.
(2)开区间上的“单峰”函数一定存在最大或最小值.5.函数的奇偶性与周期
(1)定义(2)函数奇偶性常用结论
如果函数f(x)是偶函数,那么f(x)=f(|x|).
奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.
在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.(3)周期函数
对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有f(x+T)=f(x),那么就称函数y=f(x)为周期函数,称T为这个函数的周期.6.函数的图象
(1)利用描点法画函数图象的流程(2)利用图象变换法作函数的图象
平移变换:伸缩变换: 对称变换: 翻折变换: 题型一 求函数定义域 A.(-3,0] B.(-3,1]
C.(-∞,-3)∪(-3,0] D.(-∞,-3)∪(-3,1]A.(-1,+∞) B.[-1,+∞)
C.(-1,1)∪(1,+∞) D.[-1,1)∪(1,+∞)【答案】 (1)A (2)C
【规律方法】【易错警示】求定义域时,对解析式不要化简,求出定义域后一定要将其写成集合或区间形式.
【注意】不要对解析式进行化简变形,以免定义域发生变化.变式训练一 A.(-4,-1) B.(-4,1)
C.(-1,1) D.(-1,1]C x∈(0,1] 3.(1)已知函数f(x)的定义域为(0,1),求f(x2)的定义域;
(2)已知函数f(x2)的定义域为(2,4),求f(x)的定义域;
(3)已知函数f(x2)的定义域为(1,2),求f(2x+1)的定义域.解:(1)f(x)的定义域为(0,1),即0
(3)∵f(x2)的定义域为(1,2),即1
即ax+5a+b=2x+17,不论x为何值都成立.【规律方法】求函数解析式的常用方法
(1)待定系数法:若已知函数的类型,可用待定系数法;
(2)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;式,通过解方程组求出f(x);
(4)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),即得f(x)的表达式.变式训练二 f(x)=x2-2(x≥2或x≤-2) ∴f(x)=x2-2(x≥2或x≤-2). 题型三 函数的单调性 (2)(2019·青岛模拟)已知函数f(x)=x3+sinx,x∈(-1,1),则满足f(a2-1)+f(a-1)>0的a的取值范围是( )(3)若函数f(x)=ax2+2x-3在区间(-∞,4)上是单调递增的,则实数a的取值范围是( ) (2)由题意知f(-x)=(-x)3+sin(-x)=-x3-sinx=-(x3+sinx)=-f(x),x∈(-1,1),
∴f(x)在区间(-1,1)上是奇函数.
又f'(x)=3x2+cosx>0,
∴f(x)在区间(-1,1)上单调递增,
∵f(a2-1)+f(a-1)>0,
∴-f(a-1)
(1)判断函数单调性的常用方法(2)确定函数的单调区间的方法 变式训练三 C【解析】当x=1时,loga1=0,若f(x)为R上的减函数,则(3a-1)x+4a≥0在x<1时恒成立.
令g(x)=(3a-1)x+4a.值范围是( )
A.(-∞,1] B.[1,4]
C.[4,+∞) D.(-∞,1]∪[4,+∞)D 【解析】作出f(x)的图象如图,由图象可知f(x)的单调递增区间是(-∞,2]和(4,+∞),
∵函数y=f(x)在(a,a+1)上单调递增,需满足a≥4或a+1≤2,即a≤1或a≥4.故选D.题型四 函数的奇偶性、对称性及周期性
【例4-1】 (1)判断下列函数的奇偶性.∴f(x)的定义域为{-1,1}.
又f(1)+f(-1)=0,f(1)-f(-1)=0,
∴f(x)=±f(-x).
∴f(x)既是奇函数又是偶函数.
④易知函数的定义域为(-∞,0)∪(0,+∞),关于原点对称,又当x>0时,f(x)=x2+x,
则当x<0时,-x>0,
故f(-x)=x2-x=f(x);
当x<0时,f(x)=x2-x,则当x>0时,-x<0,
故f(-x)=x2+x=f(x),故原函数是偶函数.(3)∵f(x)是定义在R上的奇函数,∴f(0)=0.
又当x<0时,-x>0,∴f(-x)=x2+4x.又f(x)为奇函数,
∴f(-x)=-f(x),
即f(x)=-x2-4x(x<0),(4)由题意,得f(-1)+f(1)=0,即2(a+1)=0,解得a=-1,经检验,a=-1时,函数f(x)为奇函数.
【答案】(1)①奇函数 ②奇函数 ③既奇又偶函数 ④偶函数 (2)-2 【例4-2】 (1)(2019·沈阳模拟)已知函数f(x)满足f(x+1)=-f(x),且当0≤x≤1时, f(1)+f(2)+f(3)+…+f(2018)的值为 .? 【解析】 (1)由f(x+1)=-f(x)得f(x+2)=-f(x+1)=f(x),即函数f(x)的周期为2, ∴f(1)+f(2)+f(3)+…+f(2018)
=504[f(1)+f(2)+f(3)+f(4)]+f(504×4+1)+f(504×4+2)=1348.
【答案】(1)A (2)A (3)1348【规律方法】
(1)判断函数周期性的方法
①定义法:判断函数的周期性只需证明f(x+T)=f(x)(T≠0)便可证明函数是周期函数,且周期为T.
②结论法:对f(x)定义域内任一自变量的值x,
ⅰ.若f(x+a)=-f(x),则T=2a(a>0);(2)函数周期性的应用,根据函数的周期性,可以由函数局部的性质得到函数的整体性质,即周期性可将未知区间上的函数值、解析式、图象转化到已知区间上,在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期.变式训练四
1.已知函数f(x)=x3+sin x+1(x∈R),若f(a)=2,则f(-a)的值为( )
A.3 B.0
C.-1 D.-2A.-1 B.-2
C.1 D.2B 【解析】 设F(x)=f(x)-1=x3+sin x,显然F(x)为奇函数,又F(a)=f(a)-1=1,所以F(-a)=f(-a)-1=-1,从而f(-a)=0.故选B.A 【解析】 因为f(x)为奇函数,所以f(-8)=-f(8)=-log39=-2,
所以g[f(-8)]=g(-2)=f(-2)=-f(2)=-log33=-1.3.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(1+x),则x<0时,f(x)= .?则下列函数值为1的是( )
A.f(2.5) B.f(f(2.5))
C.f(f(1.5)) D.f(2)x(1-x) 【解析】 当x<0时,则-x>0,
所以f(-x)=(-x)(1-x).又f(x)为奇函数,
所以f(-x)=-f(x)=(-x)(1-x),所以f(x)=x(1-x).D【解析】 由f(x+1)=-f(x)知f(x+2)=-f(x+1)=f(x),于是f(x)是以2为周期的周期函数,从而f(2.5)=f(0.5)=-1,f(f(2.5))=f(-1)=f(1)=-1,f(f(1.5))=f(f(-0.5))=f(1)=-1,f(2)=f(0)=1,故选D.5.设定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+f(3)+…+f(2019)= .?1010 【解析】 ∵f(x+2)=f(x),
∴函数f(x)的周期T=2.
又当x∈[0,2)时,f(x)=2x-x2,∴f(0)=0,f(1)=1,f(0)+f(1)=1.
∴f(0)+f(1)=f(2)+f(3)=f(4)+f(5)=…=f(2018)+f(2019)=1,
∴f(0)+f(1)+f(2)+…+f(2019)=1010.题型五 作函数图像
【例5】 作出下列函数的图象:(2)将函数y=log2x的图象向左平移1个单位,再将x轴下方的部分沿x轴翻折上去,即可得到函数y=|log2(x+1)|的图象,如图.先用描点法作出[0,+∞)上的图象,再根据对称性作出(-∞,0)上的图象,即得函数图象如图.【规律方法】函数图象的画法 变式训练五
作下列函数的图象:(2)y=x2-2x+2,x∈(-1,2];
(3)y=|x-1|,x∈R.(2)用描点法作出函数f(x)=x2-2x+2,x∈(-1,2]的图象,如图②所示. (3)可先作出y=x-1的图象,将x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变可得y=|x-1|的图象.如图③中实线部分所示.题型六 函数图象的识别
【例6】 (1)函数y=(x3-x)2|x|的图象大致是( ) A B C D (2)如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( ) A B C D 【解析】 (1)易判断函数为奇函数,由y=0得x=±1或x=0.且当0
(2)法一:由题意可知点P的轨迹为图中虚线所示,其中四个角均是半径为 的扇形.
因为矩形ABCD的周长为8,AB=x,【答案】 (1)B (2)D 【规律方法】识辨函数图象的入手点
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势.
(3)从函数的奇偶性,判断图象的对称性.
(4)从函数的周期性,判断图象的循环往复.
(5)从函数的特征点,排除不合要求的图象.变式训练六 A B C D A B B 【解析】 由定义知,当x≥0时,2x≥1,∴f(x)=2x,当x<0时,2x<1,∴f(x)=1, 4.如图,不规则四边形ABCD中,AB和CD是线段,AD和BC是圆弧,直线l⊥AB交AB于点E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,左侧部分的面积为y,则y关于x的图象大致是( )C 【解析】 当l从左至右移动时,一开始面积的增加速度越来越快,过了D点后面积保持匀速增加,图象呈直线变化,过了C点后面积的增加速度又逐渐减慢.故选C.1.若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是( )B 【解析】 可以根据函数的概念进行排除,使用筛选法得到答案. B 3.设函数f(x)=2x+3,g(x+2)=f(x),则g(x)的表达式是( )
A.g(x)=2x+1 B.g(x)=2x-1
C.g(x)=2x-3 D.g(x)=2x+7B 【解析】 令t=x+2?x=t-2,则有g(x+2)=f(x)?g(t)=f(t-2)=2(t-2)+3=2t-1. D5.(2019·开封模拟)已知f(x)是定义在R上周期为4的奇函数,当x∈(0,2]时,f(x)=2x+log2x,则f(2019)=( )
A.5 B.
C.2 D.-2D 【解析】 由题意得f(2019)=f(4×505-1)=f(-1)=-f(1)=-(21+log21)=-2,故选D. 6.下列四个函数中,在区间(0,1)上是减函数的是( ) D (0,1)上是单调递增的,故排除. 7.若函数f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是( )
A.(-1,0) B.(-1,0)∪(0,1]
C.(0,1) D.(0,1]A.c
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0B 10.y=-x2+2|x|+3的单调增区间为 .? (-∞,-1],[0,1] 由图象可以得知,函数y=-x2+2|x|+3的单调增区间为(-∞,-1],[0,1] 1.定义在R上的偶函数f(x),对任意x1,x2∈[0,+∞),(x1≠x2),有 <0,则( )
A.f(3)
且满足n∈N*时,f(-2)=f(2),3>2>1>0,得f(1)>f(-2)>f(3).2.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )
A.-3 B.-1
C.1 D.3C 【解析】∵f(x)-g(x)=x3+x2+1,∴f(-1)-g(-1)=-1+1+1=1,又∵f(x),g(x)分别是定义在R上的偶函数和奇函数,∴f(1)=f(-1),g(1)=-g(-1),∴f(-1)-g(-1)=f(1)+g(1),∴f(1)+g(1)=1.3.已知f(x)是定义在R上的奇函数,且在[0,+∞)单调递增,若f(lg x)<0,则x的取值范围是( )
A.(0,1) B.(1,10) C.(1,+∞) D.(10,+∞)A 【解析】由f(x)在定义域R上为奇函数知f(0)=0且函数图象关于原点O对称.结合f(x)在[0,+∞)上递增可知,函数在(0,+∞)上恒为正,在(-∞,0)上递增且恒为负.因为f(lgx)<0,所以lgx<0,解得x∈(0,1).
同课章节目录
