2020版高考艺考生文化课百日冲刺 第28讲 圆锥曲线(课件:104张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第28讲 圆锥曲线(课件:104张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 12:41:23 | ||
图片预览








文档简介
课件104张PPT。第28讲 圆锥曲线2.双曲线
(1)双曲线定义
平面内与两个定点F1,F2的距离之差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.
?当2a<|F1F2|时,P点的轨迹是双曲线;
?当2a=|F1F2|时,P点的轨迹是两条射线;
?当2a>|F1F2|时,P点不存在.【答案】 (1)C (2)3 D 题型二 椭圆的几何性质(高频考点)
椭圆的几何性质是每年高考的热点,主要涉及椭圆的离心率问题,题型既有选择题、填空题,也有解答题,难度中等及以上.主要命题角度有:①求椭圆的离心率问题;②椭圆中的范围问题.【答案】 (1)A (2)C 【答案】 A C C 4 D B A 2 D B D B p=2 【答案】 (1)C (2)5 (3)B (4)A 【规律方法】
(1)与双曲线几何性质有关问题的解题策略
①求双曲线的离心率(或范围).依据题设条件,将问题转化为关于a,c的等式(或不等式),解方程(或不等式)即可求得.②求双曲线的渐近线方程.依据题设条件,求双曲线中a,b的值或a与b的比值,进而得出双曲线的渐近线方程.③求双曲线焦点(焦距)、实虚轴的长.依题设条件及a,b,c之间的关系求解.
(2)确定及应用抛物线性质的技巧
①利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.②要结合图形分析,灵活运用平面几何的性质以图助解.C B C C 【答案】C 【答案】D 【规律方法】
(1)直线与圆锥曲线位置关系的判断方法
直线方程与圆锥曲线方程组成的方程组的解的个数,可以研究直线与圆锥曲线的位置关系,即用代数法研究几何问题,这是解析几何的重要思想方法.直线与圆锥曲线有无公共点或有几个公共点问题,实际上是研究方程组解的个数问题.
(2)弦长的计算方法
求弦长时可利用弦长公式,根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程,利用根与系数的关系得到两根之和、两根之积的代数式,然后进行整体代入弦长公式求解.
【注意】两种特殊情况:①直线与圆锥曲线的对称轴平行或垂直;②直线过圆锥曲线的焦点.A B B B D B D B D C A D D A B
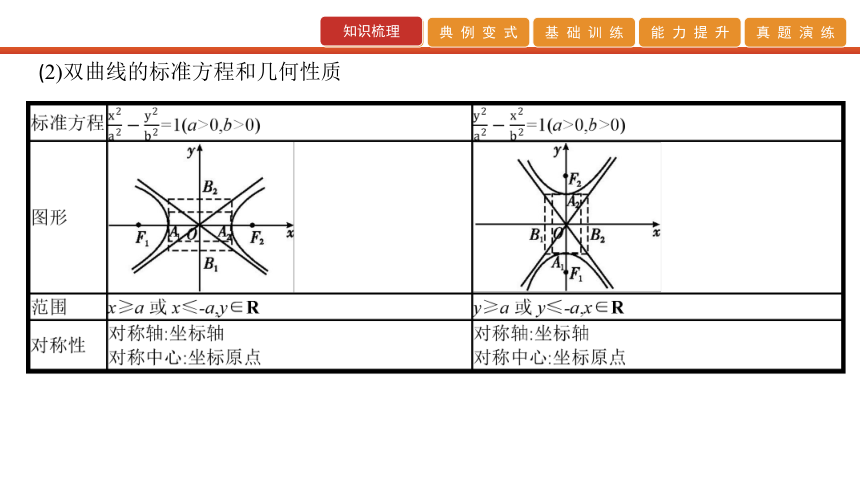
(1)双曲线定义
平面内与两个定点F1,F2的距离之差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.
?当2a<|F1F2|时,P点的轨迹是双曲线;
?当2a=|F1F2|时,P点的轨迹是两条射线;
?当2a>|F1F2|时,P点不存在.【答案】 (1)C (2)3 D 题型二 椭圆的几何性质(高频考点)
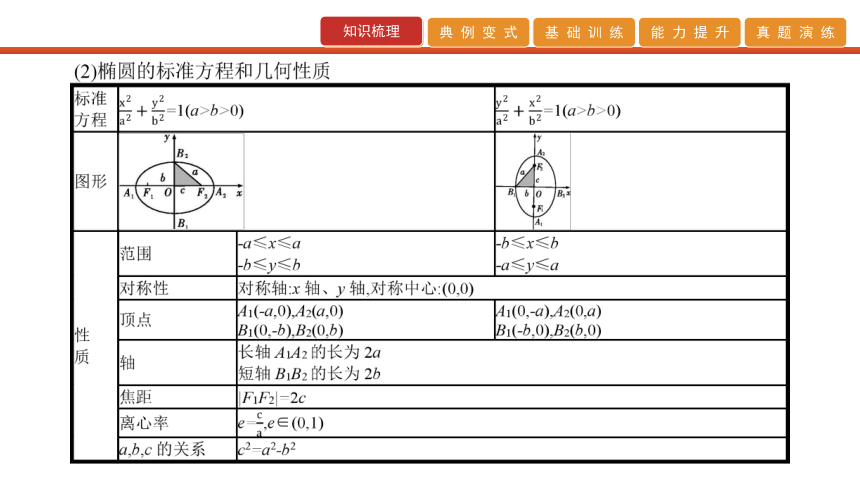
椭圆的几何性质是每年高考的热点,主要涉及椭圆的离心率问题,题型既有选择题、填空题,也有解答题,难度中等及以上.主要命题角度有:①求椭圆的离心率问题;②椭圆中的范围问题.【答案】 (1)A (2)C 【答案】 A C C 4 D B A 2 D B D B p=2 【答案】 (1)C (2)5 (3)B (4)A 【规律方法】
(1)与双曲线几何性质有关问题的解题策略
①求双曲线的离心率(或范围).依据题设条件,将问题转化为关于a,c的等式(或不等式),解方程(或不等式)即可求得.②求双曲线的渐近线方程.依据题设条件,求双曲线中a,b的值或a与b的比值,进而得出双曲线的渐近线方程.③求双曲线焦点(焦距)、实虚轴的长.依题设条件及a,b,c之间的关系求解.
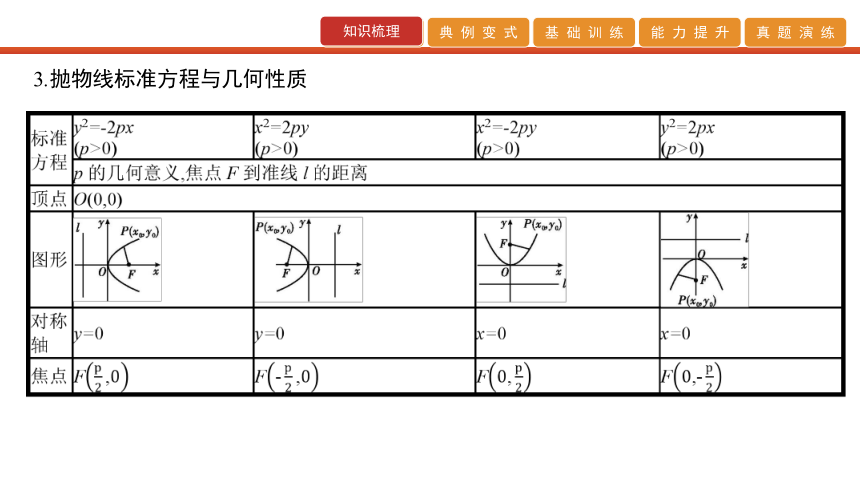
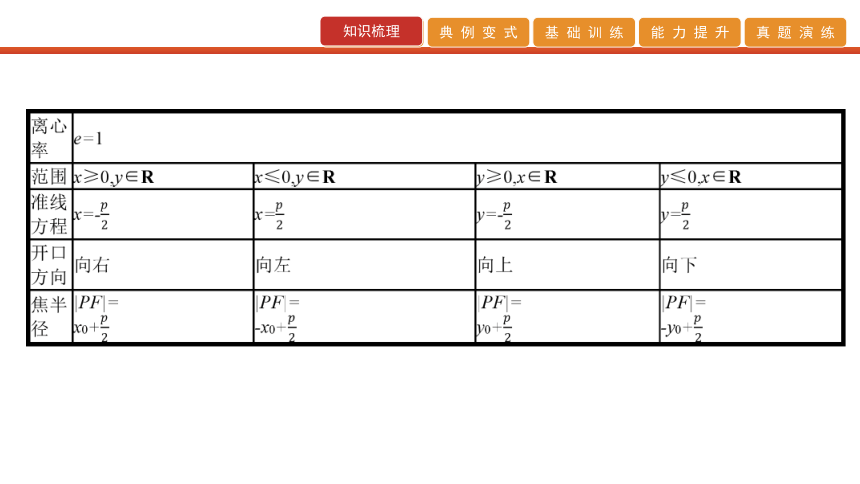
(2)确定及应用抛物线性质的技巧
①利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.②要结合图形分析,灵活运用平面几何的性质以图助解.C B C C 【答案】C 【答案】D 【规律方法】
(1)直线与圆锥曲线位置关系的判断方法
直线方程与圆锥曲线方程组成的方程组的解的个数,可以研究直线与圆锥曲线的位置关系,即用代数法研究几何问题,这是解析几何的重要思想方法.直线与圆锥曲线有无公共点或有几个公共点问题,实际上是研究方程组解的个数问题.
(2)弦长的计算方法
求弦长时可利用弦长公式,根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程,利用根与系数的关系得到两根之和、两根之积的代数式,然后进行整体代入弦长公式求解.
【注意】两种特殊情况:①直线与圆锥曲线的对称轴平行或垂直;②直线过圆锥曲线的焦点.A B B B D B D B D C A D D A B
同课章节目录
