2020版高考艺考生文化课百日冲刺 第26讲 直线与方程(课件:58张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第26讲 直线与方程(课件:58张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览







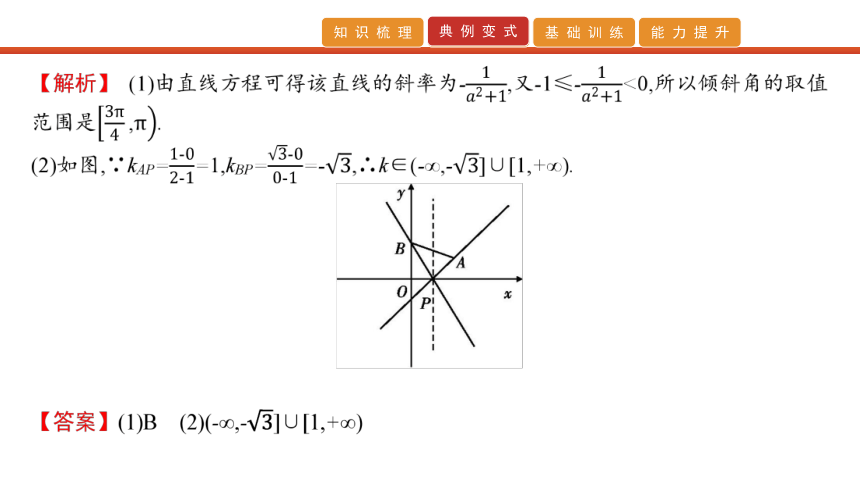




文档简介
课件58张PPT。第26讲 直线与方程B 4 【规律方法】 求直线方程的两个注意点
(1)在求直线方程时,应先选择适当的形式,并注意各种形式的适用条件.
(2)对于点斜式、截距式方程使用时要注意分类讨论思想的运用(若采用点斜式,应先考虑斜率不存在的情况;若采用截距式,应判断截距是否为零).【规律方法】 直线方程的应用问题常见的类型及解法
(1)与函数相结合命题:解决这类问题,一般是利用直线方程中x,y的关系,将问题转化成关于x的某函数,借助函数性质来解决.
(2)与方程、不等式相结合命题:一般是利用方程、不等式等知识来解决.B 3.求适合下列条件的直线方程:
(1)经过点A(-5,2),且在x轴上的截距等于在y轴上截距的2倍;
(2)经过点B(3,4),且与两坐标轴围成一个等腰直角三角形.(3,4) [0,10] ?
【解析】 设l1与l的交点为A(a,8-2a),则由题意知,点A关于点P的对称点B(-a,2a-6)在l2上,代入l2的方程得-a-3(2a-6)+10=0,解得a=4,即点A(4,0)在直线l上,所以直线l的方程为x+4y-4=0.
【答案】x+4y-4=0【答案】C 【答案】 A 【规律方法】解决两类对称问题的关键
解决中心对称问题的关键在于运用中点坐标公式,而解决轴对称问题,一般是转化为求对称点的问题,在求对称点时,关键要抓住两点:一是两对称点的连线与对称轴垂直;二是两对称点的中心在对称轴上,即抓住“垂直平分”,由“垂直”列出一个方程,由“平分”列出一个方程,联立求解.变式训练五
已知直线l:2x-3y+1=0,点A(-1,-2).求:
(1)点A关于直线l的对称点A'的坐标;
(2)直线m:3x-2y-6=0关于直线l的对称直线m'的方程;
(3)直线l关于点A(-1,-2)对称的直线l'的方程.C C C B B B D B B 2x+3y-24=0 (1,1)
(1)在求直线方程时,应先选择适当的形式,并注意各种形式的适用条件.
(2)对于点斜式、截距式方程使用时要注意分类讨论思想的运用(若采用点斜式,应先考虑斜率不存在的情况;若采用截距式,应判断截距是否为零).【规律方法】 直线方程的应用问题常见的类型及解法
(1)与函数相结合命题:解决这类问题,一般是利用直线方程中x,y的关系,将问题转化成关于x的某函数,借助函数性质来解决.
(2)与方程、不等式相结合命题:一般是利用方程、不等式等知识来解决.B 3.求适合下列条件的直线方程:
(1)经过点A(-5,2),且在x轴上的截距等于在y轴上截距的2倍;
(2)经过点B(3,4),且与两坐标轴围成一个等腰直角三角形.(3,4) [0,10] ?
【解析】 设l1与l的交点为A(a,8-2a),则由题意知,点A关于点P的对称点B(-a,2a-6)在l2上,代入l2的方程得-a-3(2a-6)+10=0,解得a=4,即点A(4,0)在直线l上,所以直线l的方程为x+4y-4=0.
【答案】x+4y-4=0【答案】C 【答案】 A 【规律方法】解决两类对称问题的关键
解决中心对称问题的关键在于运用中点坐标公式,而解决轴对称问题,一般是转化为求对称点的问题,在求对称点时,关键要抓住两点:一是两对称点的连线与对称轴垂直;二是两对称点的中心在对称轴上,即抓住“垂直平分”,由“垂直”列出一个方程,由“平分”列出一个方程,联立求解.变式训练五
已知直线l:2x-3y+1=0,点A(-1,-2).求:
(1)点A关于直线l的对称点A'的坐标;
(2)直线m:3x-2y-6=0关于直线l的对称直线m'的方程;
(3)直线l关于点A(-1,-2)对称的直线l'的方程.C C C B B B D B B 2x+3y-24=0 (1,1)
同课章节目录
