2020版高考艺考生文化课百日冲刺 第25讲 立体几何与空间向量(理)(课件:89张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第25讲 立体几何与空间向量(理)(课件:89张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览









文档简介
课件89张PPT。第25讲 立体几何与空间向量(理)1.点、线、面空间位置关系
设直线l的方向向量为a=(a1,b1,c1).平面α,β的法向量分别为u=(a2,b2,c2),v=(a3,b3,c3).
(1)线面平行:
l∥α?a⊥u?a·u=0?a1a2+b1b2+c1c2=0.
(2)线面垂直:
l⊥α?a∥u?a=ku?a1=ka2,b1=kb2,c1=kc2.
(3)面面平行:
α∥β?u∥v?u=kv?a2=ka3,b2=kb3,c2=kc3.
(4)面面垂直:
α⊥β?u⊥v?u·v=0?a2a3+b2b3+c2c3=0.2.空间角
(1)异面直线所成的角
设a,b分别是两异面直线l1,l2的方向向量,则(2)直线与平面所成的角
设直线l的方向向量为a,平面α的法向量为n,直线l与平面α所成的角为θ,则(3)二面角
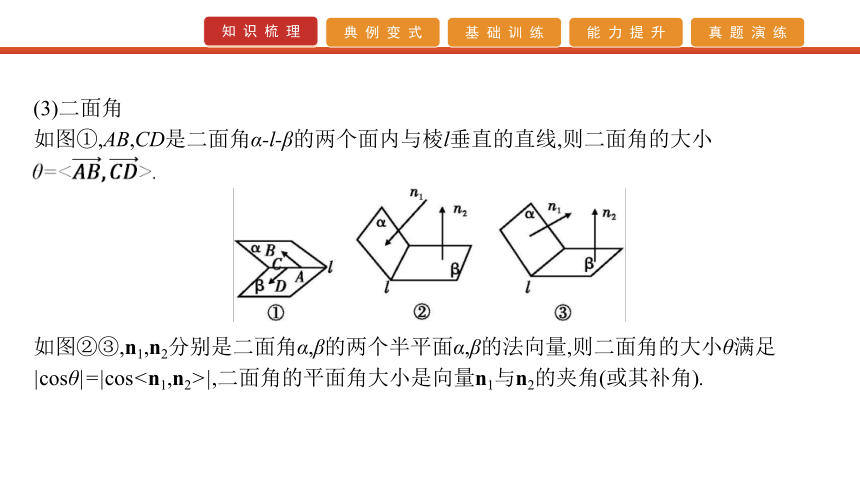
如图①,AB,CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小如图②③,n1,n2分别是二面角α,β的两个半平面α,β的法向量,则二面角的大小θ满足|cosθ|=|cos|,二面角的平面角大小是向量n1与n2的夹角(或其补角).题型一 利用空间向量证明空间位置关系
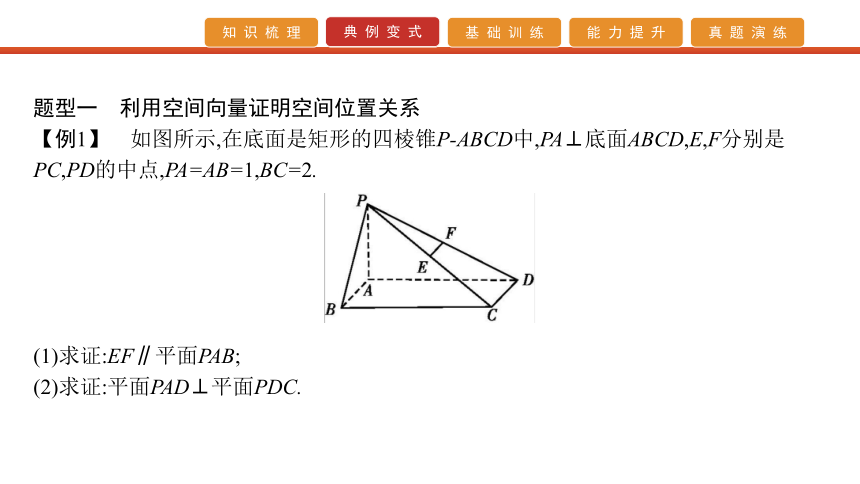
【例1】 如图所示,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=AB=1,BC=2.
(1)求证:EF∥平面PAB;
(2)求证:平面PAD⊥平面PDC.【证明】 以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1),即EF∥AB.
又AB?平面PAB,EF?平面PAB,
所以EF∥平面PAB.又AP∩AD=A,AP?平面PAD,AD?平面PAD,
所以DC⊥平面PAD.因为DC?平面PDC,
所以平面PAD⊥平面PDC.【规律方法】向量法证明平行与垂直的步骤
(1)建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系;
(2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面的要素;
(3)通过空间向量的运算求出平面向量或法向量,再研究平行、垂直关系;
(4)根据运算结果解释相关问题.变式训练一
在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1, D,F,G分别为CC1,C1B1,C1A1的中点.
求证:(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
证明:(1)以B为坐标原点,BA,BC,BB1所在的直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系B-xyz,则B(0,0,0),D(0,2,2),B1(0,0,4),设BA=a,则A(a,0,0),即B1D⊥BA,B1D⊥BD.
又BA∩BD=B,BA?平面ABD,BD?平面ABD,
因此B1D⊥平面ABD.即B1D⊥EG,B1D⊥EF.
又EG∩EF=E,EG?平面EGF,EF?平面EGF,
因此B1D⊥平面EGF.
结合(1)可知平面EGF∥平面ABD.题型二 利用空间向量求空间角
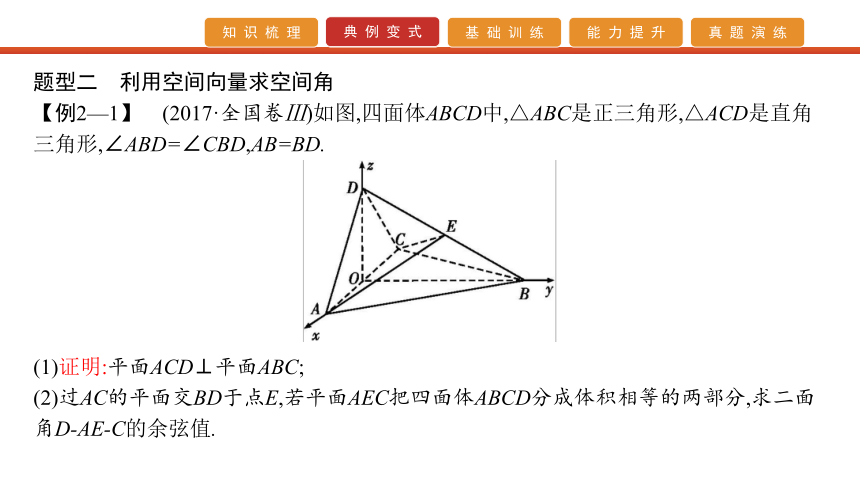
【例2—1】 (2017·全国卷Ⅲ)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.【解析】 (1)证明:由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又因为△ABC是正三角形,所以BO⊥AC.
所以∠DOB为二面角D??AC??B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,
所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.
所以平面ACD⊥平面ABC.设n=(x1,y1,z1)是平面DAE的法向量, 【例2-2】 (2019·南昌重点中学联考)如图,四边形ABCD是矩形,沿对角线AC将△ACD折起,使得点D在平面ABC内的射影恰好落在边AB上.(1)求证:平面ACD⊥平面BCD; 【解析】(1)证明:如图,设点D在平面ABC内的射影为点E,连接DE,
则DE⊥平面ABC,所以DE⊥BC.因为四边形ABCD是矩形,所以AB⊥BC,所以BC⊥平面ABD,所以BC⊥AD.
又AD⊥CD,所以AD⊥平面BCD,而AD?平面ACD,
所以平面ACD⊥平面BCD.(2)以点B为原点,线段BC所在的直线为x轴,线段AB所在的直线为y轴,建立空间直角坐标系,如图所示.
设AD=a,则AB=2a,所以A(0,-2a,0),C(-a,0,0). 【规律方法】
(1)利用空间向量求空间角的一般步骤:①建立恰当的空间直角坐标系;②求出相关点的坐标,写出相关向量的坐标;③结合公式进行论证、计算;④转化为几何结论.
(2)求空间角应注意的三个问题:①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|.②直线与平面所成的角的正弦值等于平面的法向量与直线的方向向量夹角的余弦值的绝对值,注意函数名称的变化.③两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角.变式训练二
1.(2019·太原模拟)如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
(1)证明:平面ACF⊥平面BEFD;
(2)若二面角A??EF??C是直二面角,求直线AE与平面ABCD所成角的正切值.解:(1)证明:∵四边形ABCD是菱形,∴AC⊥BD.
∵BE⊥平面ABCD,∴BE⊥AC.
∵BD∩BE=B,
∴AC⊥平面BEFD.
∵AC?平面ACF,
∴平面ACF⊥平面BEFD.(2)设AC与BD的交点为O,由(1)得AC⊥BD,分别以OA,OB为x轴和y轴,过点O作垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系O ??xyz,
∵BE⊥平面ABCD,∴BE⊥BD,
∵DF∥BE,∴DF⊥BD,
∴BD2=EF2-(DF-BE)2=8,设m=(x1,y1,z1)是平面AEF的法向量, ∵二面角A??EF??C是直二面角, 2.(2019·陕西模拟)如图,在三棱柱ABC-A1B1C1中,A1A=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.(1)求证:AB1⊥平面A1BC;
(2)若AC=5,BC=3,∠A1AB=60°,求二面角B-A1C-C1的余弦值.解:(1)证明:∵PA⊥底面ABCD,AB?底面ABCD,
∴PA⊥AB.
又AD⊥AB,PA∩AD=A,
∴AB⊥平面PAD.
∵PD?平面PAD,
∴PD⊥AB.
∵E是PD的中点,AD=AP,
∴AE⊥PD.又AE∩AB=A,
∴PD⊥平面ABE.建立如图所示的空间直角坐标系A??xyz,
令AB=2,则B(2,0,0),P(0,0,2),C(2,2,0),F(1,0,0), 令z1=1,则m=(2,-1,1)为平面PFM的一个法向量.
设平面BFM的法向量为n=(x2,y2,z2),题型三 立体几何中的探索性问题
【例3】 (2016·北京卷考)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;【解析】 (1)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
AB⊥AD,AB?平面ABCD,
所以AB⊥平面PAD.
所以AB⊥PD.
又因为PA⊥PD,PA∩AB=A,
所以PD⊥平面PAB.(2)取AD的中点O,连接PO,CO.
因为PA=PD,所以PO⊥AD.
又因为PO?平面PAD,平面PAD⊥平面ABCD,
所以PO⊥平面ABCD.
因为CO?平面ABCD,
所以PO⊥CO.
因为AC=CD,所以CO⊥AD.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1). 如图所示,建立空间直角坐标系O??xyz. 设平面PCD的法向量为n=(x,y,z), 令z=2,则x=1,y=-2.
所以n=(1,-2,2).【规律方法】 利用空间向量巧解探索性问题
(1)空间向量最适合于解决立体几何中的探索性问题,它无须进行复杂的作图、论证、推理,只需通过坐标运算进行判断.
(2)解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等问题,所以为使问题的解决更简单、有效,应善于运用这一方法解题.
【提醒】探索线段上是否存在点时,注意三点共线条件的应用.变式训练三
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.解:(1)以D为坐标原点,以DA,DC,DM为x轴,y轴,z轴建立空间直角坐标系D??xyz. (2)假设在线段AN上存在点S,使得ES⊥平面AMN.连接AE,ES. 1.(2018·惠州三调)如图,四边形ABCD是圆柱OQ的轴截面,点P在圆柱OQ的底面圆周上,G是DP的中点,圆柱OQ的底面圆的半径OA=2,侧面积为8 π,∠AOP=120°.(1)求证:AG⊥BD;
(2)求二面角P-AG-B的余弦值.解:建立如图所示的空间直角坐标系, 作PE⊥AB,垂足为E,
∵OP=OA=2,∠AOP=120°,
∴∠EOP=60°,PE= ,OE=1,∴AE=AO+OE=3.∴AG⊥BD. 2.(2018·陕西模拟)如图,在三棱柱ABC-A1B1C1中,A1A=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.(1)求证:AB1⊥平面A1BC;
(2)若AC=5,BC=3,∠A1AB=60°,求二面角B-A1C-C1的余弦值.解: (1)证明:在侧面A1ABB1中,∵A1A=AB,
∴四边形A1ABB1为菱形,∴AB1⊥A1B.
∵侧面A1ABB1⊥底面ABC,∠ABC=90°,
平面A1ABB1∩平面ABC=AB,
∴CB⊥侧面A1ABB1.
∵AB1?平面A1ABB1,∴CB⊥AB1.
又∵A1B∩BC=B,∴AB1⊥平面A1BC.(2)在Rt△ABC中,AC=5,BC=3,∴AB=4,
在菱形A1ABB1中,
∵∠A1AB=60°,
∴△A1AB为正三角形.
如图,以菱形A1ABB1的对角线交点O为坐标原点,OA1所在直线为x轴,OA所在直线为y轴,过点O且与BC平行的直线为z轴建立如图所示空间直角坐标系,3.(2018·成都一诊)如图①,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF 分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图②所示.(1)若λ=2,求证:GR⊥平面PEF; 的值;若不存在,请说明理由. 解:(1)证明:由题意,可知PE,PF,PD三条直线两两垂直.
∴PD⊥平面PEF.
在图①中,∵E,F分别是AB,BC的中点,G为BD的中点,∴EF∥AC,GD=GB=2GH.∴在△PDH中,GR∥PD.
∴GR⊥平面PEF.
(2)由题意,分别以PF,PE,PD所在直线为x轴,y轴,
z轴建立如图所示的空间直角坐标系P??xyz.
设PD=4,则P(0,0,0),F(2,0,0),E(0,2,0),D(0,0,4), (1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由.1.将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C,如图2.所以AD=1,AE=2.
在△ADE中,∠DAE=60°,
由余弦定理得从而AD2+DE2=AE2,所以AD⊥DE.
折起后有A1D⊥DE,因为二面角A1-DE-B是直二面角,
所以平面A1DE⊥平面BCED,
又平面A1DE∩平面BCED=DE,
A1D⊥DE,所以A1D⊥平面BCED.(2)存在.理由:由(1)可知ED⊥DB,A1D⊥平面BCED.
以D为坐标原点,分别以DB,DE,DA1所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz.
设PB=2a(0≤2a≤3),
作PH⊥BD于点H,
连接A1H,A1P,2.(2018·湖北五校联考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M-AC-D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.解:(1)证明:如图,由已知得四边形ABCD是直角梯形, 可得AB=AC=4,
所以BC2=AB2+AC2,
所以∠BAC=90°,即AB⊥AC,
因为PA⊥平面ABCD,所以PA⊥AB,
又PA∩AC=A,
所以AB⊥平面PAC,所以AB⊥PC.(2)存在,理由如下:取BC的中点E,则AE⊥BC,以A为坐标原点,AE,AD,AP所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,又m=(0,0,1)是平面ACD的一个法向量, 一、选择题
1.(2018·北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
A.1 B.2 C.3 D.4C 【解析】 由三视图可得四棱锥P??ABCD,
在四棱锥P??ABCD中,PD=2,AD=2,CD=2,AB=1,则在四棱锥中,直角三角形有:△PAD,△PCD,△PAB共三个,故选C.2.(2019·全国卷Ⅱ文理)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面B 【解析】 由面面平行的判定定理知:α内两条相交直线都与β平行是α//β的充分条件,由面面平行性质定理知,若α//β,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是α//β的必要条件,故选B.3.(201·全国卷Ⅰ)在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为( )C 【解析】 在长方体ABCD??A1B1C1D1中,连接BC1,
根据线面角的定义可知∠AC1B=30°,4.(2018·全国卷Ⅱ)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )C 【解析】 在正方体ABCD??A1B1C1D1中,CD∥AB,
所以异面直线AE与CD所成角为∠EAB,
设正方体边长为2a,
则由E为棱CC1的中点,可得CE=a,故选C. 5.(2019·全国卷Ⅰ理)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,PB的中点,∠CEF=90°,则球O的体积为( )D 【解析】 解法一:∵PA=PB=PC,△ABC为边长为2的等边三角形,
∴P-ABC为正三棱锥,
∴PB⊥AC,又E,F分别为PA,AB的中点,
∴EF//PB,∴EF⊥AC,又EF⊥CE,CE∩AC=C,解法二:
设PA=PB=PC=2x,E,F分别为PA,AB中点,二、填空题
6.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .?【解析】 由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正 7.(2018·天津卷)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为 .?【解析】 如图所示,连结A1C1,交B1D1于点O,很明显A1C1⊥平面BDD1B1, 8.(2018·全国卷Ⅱ)已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°,若△SAB的面积为8,则该圆锥的体积为 .?8π 【解析】 如下图所示,∠SAO=30°,∠ASB=90°, 9.(2019·全国卷Ⅰ文)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为 .?【解析】 作PD,PE分别垂直于AC,BC,PO⊥平面ABC,连CO,
知CD⊥PD,CD⊥PO,PD∩OD=D,
∴CD⊥平面PDO,OD?平面PDO,
∴CD⊥OD.10.(2019·全国卷Ⅱ文理)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有 个面,其棱长为 .?26 【解析】 由图可知第一层与第三层各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有18+8=26个面.
如图,设该半正多面体的棱长为x,则AB=BE=x,延长CB与FE交于点G,延长BC交正方体棱于H,由半正多面体对称性可知,△BGE为等腰直角三角形,三、解答题
11.(2018·江苏卷)在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1。
求证:(1)AB∥平面A1B1C;
(2)平面ABB1A1⊥平面A1BC.证明:(1)在平行六面体ABCD??A1B1C1D1中,AB∥A1B1.
因为AB?平面A1B1C,A1B1?平面A1B1C,
所以AB∥平面A1B1C.
(2)在平行六面体ABCD??A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,A1B?平面A1BC,BC?平面A1BC,
所以AB1⊥平面A1BC.
因为AB1?平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.12.(2018·北京卷)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.
(1)求证:PE⊥BC;
(2)求证:平面PAB⊥平面PCD;
(3)求证:EF∥平面PCD.证明:(1)∵PA=PD,且E为AD的中点,
∴PE⊥AD.
∵底面ABCD为矩形,∴BC∥AD,
∴PE⊥BC.
(2)∵底面ABCD为矩形,
∴AB⊥AD.
∵平面PAD⊥平面ABCD,
∴AB⊥平面PAD.
∴AB⊥PD.又PA⊥PD,
∵PD⊥平面PAB,
∴平面PAB⊥平面PCD.(3)如图,取PC中点G,连接FG,GD.
∵F,G分别为PB和PC的中点,
∴PG∥BC,且FG= BC.
∵四边形ABCD为矩形,且E为AD的中点,
∴ED∥BC,DE= BC,
∴ED∥FG,且ED=FG,
∴四边形EFGD为平行四边形,
∴EF∥GD.
又EF?平面PCD,GD?平面PCD,
∴EF∥平面PCD.13.(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ= DA,求三棱锥Q-ABP的体积.解:(1)证明:由已知可得,∠BAC=90°,BA⊥AC.
又BA⊥AD,且AC∩AD=A,所以AB⊥平面ACD.
又AB?平面ABC,
所以平面ACD⊥平面ABC.由已知及(1)可得DC⊥平面ABC,
所以QE⊥平面ABC,QE=1.
因此,三棱锥Q??ABP的体积为14.(2018·全国卷Ⅱ)如图,在三棱锥P-ABC中,AB=BC=2 ,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.由OP2+OB2=PB2知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,
所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.15.(2019·全国卷Ⅰ文)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, ∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.解:(1)连接ME,B1C,
∵M,E分别为BB1,BC中点,∴ME为△B1BC的中位线,∴ME??ND,∴四边形MNDE为平行四边形,
∴MN//DE,又MN?平面C1DE,DE?平面C1DE,
∴MN//平面C1DE.(2)在菱形ABCD中,E为BC中点,所以DE⊥BC, 15.(2019·全国卷Ⅰ理)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.解:(1)证明:连接ME,B1C,
∵M,E分别为BB1,BC中点,∴ME为ΔB1BC的中位线∴ME??ND,∴四边形MNDE为平行四边形,
∴MN//DE,又MN?平面C1DE,DE?平面C1DE,
∴MN//平面C1DE.(2)设AC∩BD=O,A1C1∩B1D1=O1.
由直四棱柱性质可知:OO1⊥平面ABCD.
∵四边形ABCD为菱形,∴AC⊥BD.
则以O为原点,可建立如下图所示的空间直角坐标系:∵四边形ABCD为菱形且∠BAD=60°,
∴△BAD为等边三角形,
∴DF⊥AB,
又AA1⊥平面ABCD,DF?平面ABCD,∴DF⊥AA1,
∴DF⊥平面ABB1A1,即DF⊥平面AMA1,16.(2019·全国卷Ⅱ文)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.解:(1)证明:因为在长方体ABCD-A1B1C1D1中,B1C1⊥平面ABB1A1;
BE?平面ABB1A1,所以B1C1⊥BE,
又BE⊥EC1,B1C1∩EC1=C1,且EC1?平面EB1C1,B1C1?平面EB1C1,
所以BE⊥平面EB1C1;
(2)设长方体侧棱长为2a,则AE=A1E=a,16.(2019·全国卷Ⅱ理)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.解:(1)证明:因为ABCD-A1B1C1D1是长方体,所以B1C1⊥侧面A1B1BA,而BE?平面A1B1BA,所以BE⊥B1C1,
又BE⊥EC1,B1C1∩EC1=C1,B1C1,EC1?平面EB1C1,因此BE⊥平面EB1C1;设n=(x2,y2,z2)是平面ECC1的法向量,
设直线l的方向向量为a=(a1,b1,c1).平面α,β的法向量分别为u=(a2,b2,c2),v=(a3,b3,c3).
(1)线面平行:
l∥α?a⊥u?a·u=0?a1a2+b1b2+c1c2=0.
(2)线面垂直:
l⊥α?a∥u?a=ku?a1=ka2,b1=kb2,c1=kc2.
(3)面面平行:
α∥β?u∥v?u=kv?a2=ka3,b2=kb3,c2=kc3.
(4)面面垂直:
α⊥β?u⊥v?u·v=0?a2a3+b2b3+c2c3=0.2.空间角
(1)异面直线所成的角
设a,b分别是两异面直线l1,l2的方向向量,则(2)直线与平面所成的角
设直线l的方向向量为a,平面α的法向量为n,直线l与平面α所成的角为θ,则(3)二面角
如图①,AB,CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小如图②③,n1,n2分别是二面角α,β的两个半平面α,β的法向量,则二面角的大小θ满足|cosθ|=|cos
【例1】 如图所示,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=AB=1,BC=2.
(1)求证:EF∥平面PAB;
(2)求证:平面PAD⊥平面PDC.【证明】 以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1),即EF∥AB.
又AB?平面PAB,EF?平面PAB,
所以EF∥平面PAB.又AP∩AD=A,AP?平面PAD,AD?平面PAD,
所以DC⊥平面PAD.因为DC?平面PDC,
所以平面PAD⊥平面PDC.【规律方法】向量法证明平行与垂直的步骤
(1)建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系;
(2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面的要素;
(3)通过空间向量的运算求出平面向量或法向量,再研究平行、垂直关系;
(4)根据运算结果解释相关问题.变式训练一
在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1, D,F,G分别为CC1,C1B1,C1A1的中点.
求证:(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
证明:(1)以B为坐标原点,BA,BC,BB1所在的直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系B-xyz,则B(0,0,0),D(0,2,2),B1(0,0,4),设BA=a,则A(a,0,0),即B1D⊥BA,B1D⊥BD.
又BA∩BD=B,BA?平面ABD,BD?平面ABD,
因此B1D⊥平面ABD.即B1D⊥EG,B1D⊥EF.
又EG∩EF=E,EG?平面EGF,EF?平面EGF,
因此B1D⊥平面EGF.
结合(1)可知平面EGF∥平面ABD.题型二 利用空间向量求空间角
【例2—1】 (2017·全国卷Ⅲ)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.【解析】 (1)证明:由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又因为△ABC是正三角形,所以BO⊥AC.
所以∠DOB为二面角D??AC??B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,
所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.
所以平面ACD⊥平面ABC.设n=(x1,y1,z1)是平面DAE的法向量, 【例2-2】 (2019·南昌重点中学联考)如图,四边形ABCD是矩形,沿对角线AC将△ACD折起,使得点D在平面ABC内的射影恰好落在边AB上.(1)求证:平面ACD⊥平面BCD; 【解析】(1)证明:如图,设点D在平面ABC内的射影为点E,连接DE,
则DE⊥平面ABC,所以DE⊥BC.因为四边形ABCD是矩形,所以AB⊥BC,所以BC⊥平面ABD,所以BC⊥AD.
又AD⊥CD,所以AD⊥平面BCD,而AD?平面ACD,
所以平面ACD⊥平面BCD.(2)以点B为原点,线段BC所在的直线为x轴,线段AB所在的直线为y轴,建立空间直角坐标系,如图所示.
设AD=a,则AB=2a,所以A(0,-2a,0),C(-a,0,0). 【规律方法】
(1)利用空间向量求空间角的一般步骤:①建立恰当的空间直角坐标系;②求出相关点的坐标,写出相关向量的坐标;③结合公式进行论证、计算;④转化为几何结论.
(2)求空间角应注意的三个问题:①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|.②直线与平面所成的角的正弦值等于平面的法向量与直线的方向向量夹角的余弦值的绝对值,注意函数名称的变化.③两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角.变式训练二
1.(2019·太原模拟)如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
(1)证明:平面ACF⊥平面BEFD;
(2)若二面角A??EF??C是直二面角,求直线AE与平面ABCD所成角的正切值.解:(1)证明:∵四边形ABCD是菱形,∴AC⊥BD.
∵BE⊥平面ABCD,∴BE⊥AC.
∵BD∩BE=B,
∴AC⊥平面BEFD.
∵AC?平面ACF,
∴平面ACF⊥平面BEFD.(2)设AC与BD的交点为O,由(1)得AC⊥BD,分别以OA,OB为x轴和y轴,过点O作垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系O ??xyz,
∵BE⊥平面ABCD,∴BE⊥BD,
∵DF∥BE,∴DF⊥BD,
∴BD2=EF2-(DF-BE)2=8,设m=(x1,y1,z1)是平面AEF的法向量, ∵二面角A??EF??C是直二面角, 2.(2019·陕西模拟)如图,在三棱柱ABC-A1B1C1中,A1A=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.(1)求证:AB1⊥平面A1BC;
(2)若AC=5,BC=3,∠A1AB=60°,求二面角B-A1C-C1的余弦值.解:(1)证明:∵PA⊥底面ABCD,AB?底面ABCD,
∴PA⊥AB.
又AD⊥AB,PA∩AD=A,
∴AB⊥平面PAD.
∵PD?平面PAD,
∴PD⊥AB.
∵E是PD的中点,AD=AP,
∴AE⊥PD.又AE∩AB=A,
∴PD⊥平面ABE.建立如图所示的空间直角坐标系A??xyz,
令AB=2,则B(2,0,0),P(0,0,2),C(2,2,0),F(1,0,0), 令z1=1,则m=(2,-1,1)为平面PFM的一个法向量.
设平面BFM的法向量为n=(x2,y2,z2),题型三 立体几何中的探索性问题
【例3】 (2016·北京卷考)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;【解析】 (1)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
AB⊥AD,AB?平面ABCD,
所以AB⊥平面PAD.
所以AB⊥PD.
又因为PA⊥PD,PA∩AB=A,
所以PD⊥平面PAB.(2)取AD的中点O,连接PO,CO.
因为PA=PD,所以PO⊥AD.
又因为PO?平面PAD,平面PAD⊥平面ABCD,
所以PO⊥平面ABCD.
因为CO?平面ABCD,
所以PO⊥CO.
因为AC=CD,所以CO⊥AD.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1). 如图所示,建立空间直角坐标系O??xyz. 设平面PCD的法向量为n=(x,y,z), 令z=2,则x=1,y=-2.
所以n=(1,-2,2).【规律方法】 利用空间向量巧解探索性问题
(1)空间向量最适合于解决立体几何中的探索性问题,它无须进行复杂的作图、论证、推理,只需通过坐标运算进行判断.
(2)解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等问题,所以为使问题的解决更简单、有效,应善于运用这一方法解题.
【提醒】探索线段上是否存在点时,注意三点共线条件的应用.变式训练三
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.解:(1)以D为坐标原点,以DA,DC,DM为x轴,y轴,z轴建立空间直角坐标系D??xyz. (2)假设在线段AN上存在点S,使得ES⊥平面AMN.连接AE,ES. 1.(2018·惠州三调)如图,四边形ABCD是圆柱OQ的轴截面,点P在圆柱OQ的底面圆周上,G是DP的中点,圆柱OQ的底面圆的半径OA=2,侧面积为8 π,∠AOP=120°.(1)求证:AG⊥BD;
(2)求二面角P-AG-B的余弦值.解:建立如图所示的空间直角坐标系, 作PE⊥AB,垂足为E,
∵OP=OA=2,∠AOP=120°,
∴∠EOP=60°,PE= ,OE=1,∴AE=AO+OE=3.∴AG⊥BD. 2.(2018·陕西模拟)如图,在三棱柱ABC-A1B1C1中,A1A=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.(1)求证:AB1⊥平面A1BC;
(2)若AC=5,BC=3,∠A1AB=60°,求二面角B-A1C-C1的余弦值.解: (1)证明:在侧面A1ABB1中,∵A1A=AB,
∴四边形A1ABB1为菱形,∴AB1⊥A1B.
∵侧面A1ABB1⊥底面ABC,∠ABC=90°,
平面A1ABB1∩平面ABC=AB,
∴CB⊥侧面A1ABB1.
∵AB1?平面A1ABB1,∴CB⊥AB1.
又∵A1B∩BC=B,∴AB1⊥平面A1BC.(2)在Rt△ABC中,AC=5,BC=3,∴AB=4,
在菱形A1ABB1中,
∵∠A1AB=60°,
∴△A1AB为正三角形.
如图,以菱形A1ABB1的对角线交点O为坐标原点,OA1所在直线为x轴,OA所在直线为y轴,过点O且与BC平行的直线为z轴建立如图所示空间直角坐标系,3.(2018·成都一诊)如图①,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF 分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图②所示.(1)若λ=2,求证:GR⊥平面PEF; 的值;若不存在,请说明理由. 解:(1)证明:由题意,可知PE,PF,PD三条直线两两垂直.
∴PD⊥平面PEF.
在图①中,∵E,F分别是AB,BC的中点,G为BD的中点,∴EF∥AC,GD=GB=2GH.∴在△PDH中,GR∥PD.
∴GR⊥平面PEF.
(2)由题意,分别以PF,PE,PD所在直线为x轴,y轴,
z轴建立如图所示的空间直角坐标系P??xyz.
设PD=4,则P(0,0,0),F(2,0,0),E(0,2,0),D(0,0,4), (1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由.1.将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C,如图2.所以AD=1,AE=2.
在△ADE中,∠DAE=60°,
由余弦定理得从而AD2+DE2=AE2,所以AD⊥DE.
折起后有A1D⊥DE,因为二面角A1-DE-B是直二面角,
所以平面A1DE⊥平面BCED,
又平面A1DE∩平面BCED=DE,
A1D⊥DE,所以A1D⊥平面BCED.(2)存在.理由:由(1)可知ED⊥DB,A1D⊥平面BCED.
以D为坐标原点,分别以DB,DE,DA1所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz.
设PB=2a(0≤2a≤3),
作PH⊥BD于点H,
连接A1H,A1P,2.(2018·湖北五校联考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M-AC-D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.解:(1)证明:如图,由已知得四边形ABCD是直角梯形, 可得AB=AC=4,
所以BC2=AB2+AC2,
所以∠BAC=90°,即AB⊥AC,
因为PA⊥平面ABCD,所以PA⊥AB,
又PA∩AC=A,
所以AB⊥平面PAC,所以AB⊥PC.(2)存在,理由如下:取BC的中点E,则AE⊥BC,以A为坐标原点,AE,AD,AP所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,又m=(0,0,1)是平面ACD的一个法向量, 一、选择题
1.(2018·北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
A.1 B.2 C.3 D.4C 【解析】 由三视图可得四棱锥P??ABCD,
在四棱锥P??ABCD中,PD=2,AD=2,CD=2,AB=1,则在四棱锥中,直角三角形有:△PAD,△PCD,△PAB共三个,故选C.2.(2019·全国卷Ⅱ文理)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面B 【解析】 由面面平行的判定定理知:α内两条相交直线都与β平行是α//β的充分条件,由面面平行性质定理知,若α//β,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是α//β的必要条件,故选B.3.(201·全国卷Ⅰ)在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为( )C 【解析】 在长方体ABCD??A1B1C1D1中,连接BC1,
根据线面角的定义可知∠AC1B=30°,4.(2018·全国卷Ⅱ)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )C 【解析】 在正方体ABCD??A1B1C1D1中,CD∥AB,
所以异面直线AE与CD所成角为∠EAB,
设正方体边长为2a,
则由E为棱CC1的中点,可得CE=a,故选C. 5.(2019·全国卷Ⅰ理)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,PB的中点,∠CEF=90°,则球O的体积为( )D 【解析】 解法一:∵PA=PB=PC,△ABC为边长为2的等边三角形,
∴P-ABC为正三棱锥,
∴PB⊥AC,又E,F分别为PA,AB的中点,
∴EF//PB,∴EF⊥AC,又EF⊥CE,CE∩AC=C,解法二:
设PA=PB=PC=2x,E,F分别为PA,AB中点,二、填空题
6.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .?【解析】 由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正 7.(2018·天津卷)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为 .?【解析】 如图所示,连结A1C1,交B1D1于点O,很明显A1C1⊥平面BDD1B1, 8.(2018·全国卷Ⅱ)已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°,若△SAB的面积为8,则该圆锥的体积为 .?8π 【解析】 如下图所示,∠SAO=30°,∠ASB=90°, 9.(2019·全国卷Ⅰ文)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为 .?【解析】 作PD,PE分别垂直于AC,BC,PO⊥平面ABC,连CO,
知CD⊥PD,CD⊥PO,PD∩OD=D,
∴CD⊥平面PDO,OD?平面PDO,
∴CD⊥OD.10.(2019·全国卷Ⅱ文理)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有 个面,其棱长为 .?26 【解析】 由图可知第一层与第三层各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有18+8=26个面.
如图,设该半正多面体的棱长为x,则AB=BE=x,延长CB与FE交于点G,延长BC交正方体棱于H,由半正多面体对称性可知,△BGE为等腰直角三角形,三、解答题
11.(2018·江苏卷)在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1。
求证:(1)AB∥平面A1B1C;
(2)平面ABB1A1⊥平面A1BC.证明:(1)在平行六面体ABCD??A1B1C1D1中,AB∥A1B1.
因为AB?平面A1B1C,A1B1?平面A1B1C,
所以AB∥平面A1B1C.
(2)在平行六面体ABCD??A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,A1B?平面A1BC,BC?平面A1BC,
所以AB1⊥平面A1BC.
因为AB1?平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.12.(2018·北京卷)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.
(1)求证:PE⊥BC;
(2)求证:平面PAB⊥平面PCD;
(3)求证:EF∥平面PCD.证明:(1)∵PA=PD,且E为AD的中点,
∴PE⊥AD.
∵底面ABCD为矩形,∴BC∥AD,
∴PE⊥BC.
(2)∵底面ABCD为矩形,
∴AB⊥AD.
∵平面PAD⊥平面ABCD,
∴AB⊥平面PAD.
∴AB⊥PD.又PA⊥PD,
∵PD⊥平面PAB,
∴平面PAB⊥平面PCD.(3)如图,取PC中点G,连接FG,GD.
∵F,G分别为PB和PC的中点,
∴PG∥BC,且FG= BC.
∵四边形ABCD为矩形,且E为AD的中点,
∴ED∥BC,DE= BC,
∴ED∥FG,且ED=FG,
∴四边形EFGD为平行四边形,
∴EF∥GD.
又EF?平面PCD,GD?平面PCD,
∴EF∥平面PCD.13.(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ= DA,求三棱锥Q-ABP的体积.解:(1)证明:由已知可得,∠BAC=90°,BA⊥AC.
又BA⊥AD,且AC∩AD=A,所以AB⊥平面ACD.
又AB?平面ABC,
所以平面ACD⊥平面ABC.由已知及(1)可得DC⊥平面ABC,
所以QE⊥平面ABC,QE=1.
因此,三棱锥Q??ABP的体积为14.(2018·全国卷Ⅱ)如图,在三棱锥P-ABC中,AB=BC=2 ,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.由OP2+OB2=PB2知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,
所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.15.(2019·全国卷Ⅰ文)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, ∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.解:(1)连接ME,B1C,
∵M,E分别为BB1,BC中点,∴ME为△B1BC的中位线,∴ME??ND,∴四边形MNDE为平行四边形,
∴MN//DE,又MN?平面C1DE,DE?平面C1DE,
∴MN//平面C1DE.(2)在菱形ABCD中,E为BC中点,所以DE⊥BC, 15.(2019·全国卷Ⅰ理)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.解:(1)证明:连接ME,B1C,
∵M,E分别为BB1,BC中点,∴ME为ΔB1BC的中位线∴ME??ND,∴四边形MNDE为平行四边形,
∴MN//DE,又MN?平面C1DE,DE?平面C1DE,
∴MN//平面C1DE.(2)设AC∩BD=O,A1C1∩B1D1=O1.
由直四棱柱性质可知:OO1⊥平面ABCD.
∵四边形ABCD为菱形,∴AC⊥BD.
则以O为原点,可建立如下图所示的空间直角坐标系:∵四边形ABCD为菱形且∠BAD=60°,
∴△BAD为等边三角形,
∴DF⊥AB,
又AA1⊥平面ABCD,DF?平面ABCD,∴DF⊥AA1,
∴DF⊥平面ABB1A1,即DF⊥平面AMA1,16.(2019·全国卷Ⅱ文)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.解:(1)证明:因为在长方体ABCD-A1B1C1D1中,B1C1⊥平面ABB1A1;
BE?平面ABB1A1,所以B1C1⊥BE,
又BE⊥EC1,B1C1∩EC1=C1,且EC1?平面EB1C1,B1C1?平面EB1C1,
所以BE⊥平面EB1C1;
(2)设长方体侧棱长为2a,则AE=A1E=a,16.(2019·全国卷Ⅱ理)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.解:(1)证明:因为ABCD-A1B1C1D1是长方体,所以B1C1⊥侧面A1B1BA,而BE?平面A1B1BA,所以BE⊥B1C1,
又BE⊥EC1,B1C1∩EC1=C1,B1C1,EC1?平面EB1C1,因此BE⊥平面EB1C1;设n=(x2,y2,z2)是平面ECC1的法向量,
同课章节目录
