24.4.3 切线长定理(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.4.3 切线长定理(基础达标+巩固提升+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览

文档简介
沪科版数学九年级下册同步课时训练
第24章 圆
24.4 直线与圆的位置关系
第3课时 切线长定理
要点测评 基础达标
要点1 切线长和切线长定理
1. 如图,☉O的半径是3,点P到圆心O的距离是6,PA,PB分别和☉O相切于点A,B,则切线长PA= ,∠APB的度数是 .?
2. 如图,P是☉O外的一点,PA,PB分别与☉O相切于点A,B,C是弧AB上的任意一点,过点C的切线分别交PA,PB于点D,E.若PA=4,求△PED的周长.
要点2 切线长定理的应用
3. 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3 cm,则此光盘的直径是 .?
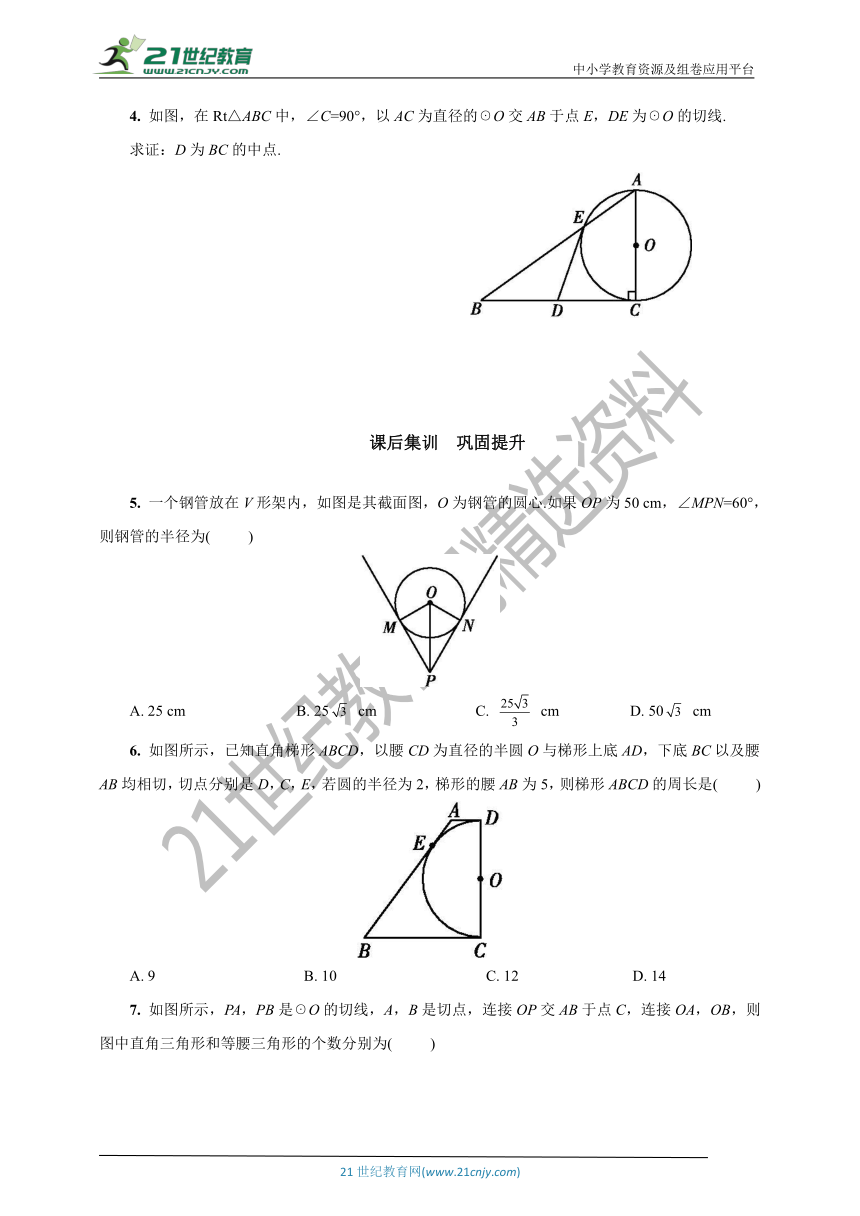
4. 如图,在Rt△ABC中,∠C=90°,以AC为直径的☉O交AB于点E,DE为☉O的切线.
求证:D为BC的中点.
课后集训 巩固提升
5. 一个钢管放在V形架内,如图是其截面图,O为钢管的圆心.如果OP为50 cm,∠MPN=60°,则钢管的半径为( )
A. 25 cm B. 25 cm C. cm D. 50 cm
6. 如图所示,已知直角梯形ABCD,以腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E,若圆的半径为2,梯形的腰AB为5,则梯形ABCD的周长是( )
A. 9 B. 10 C. 12 D. 14
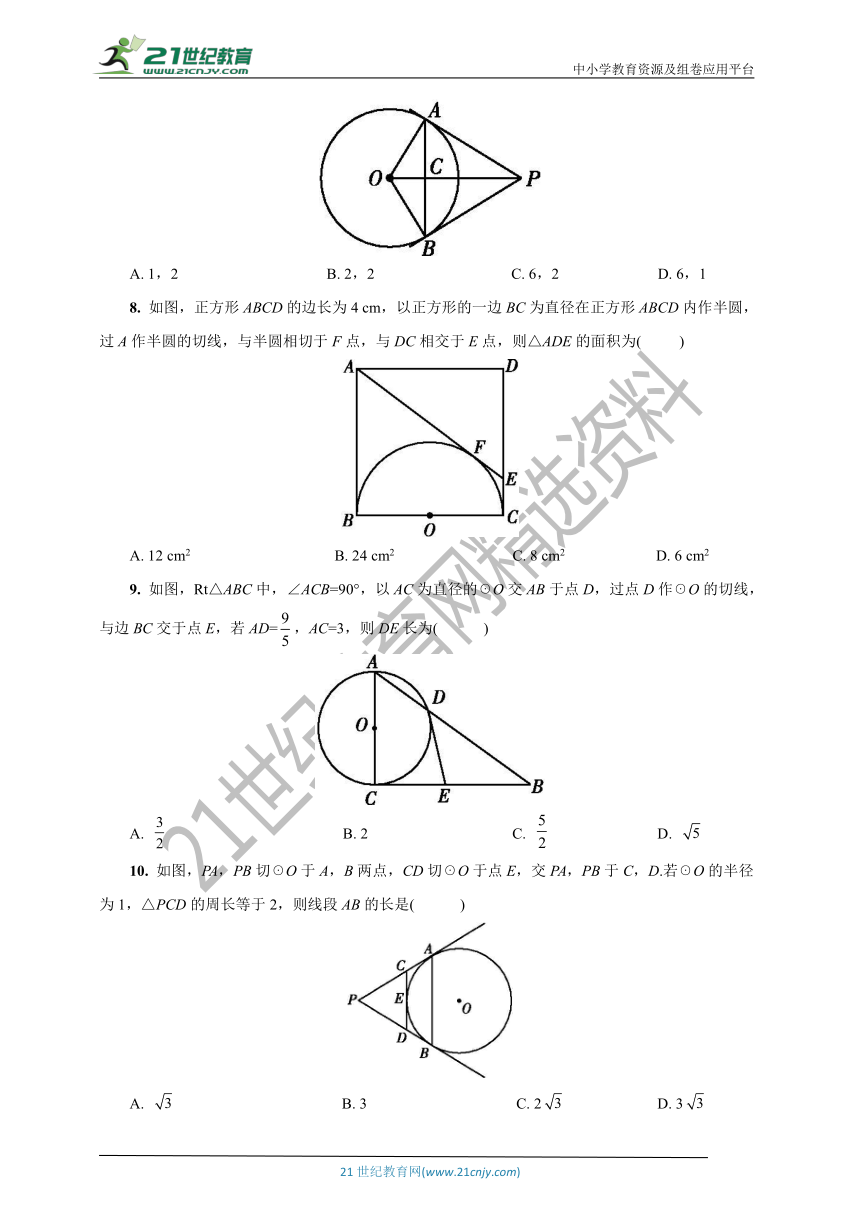
7. 如图所示,PA,PB是☉O的切线,A,B是切点,连接OP交AB于点C,连接OA,OB,则图中直角三角形和等腰三角形的个数分别为( )
A. 1,2 B. 2,2 C. 6,2 D. 6,1
8. 如图,正方形ABCD的边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积为( )
A. 12 cm2 B. 24 cm2 C. 8 cm2 D. 6 cm2
9. 如图,Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线,与边BC交于点E,若AD=,AC=3,则DE长为( )
A. B. 2 C. D.
10. 如图,PA,PB切☉O于A,B两点,CD切☉O于点E,交PA,PB于C,D.若☉O的半径为1,△PCD的周长等于2,则线段AB的长是( )
A. B. 3 C. 2 D. 3
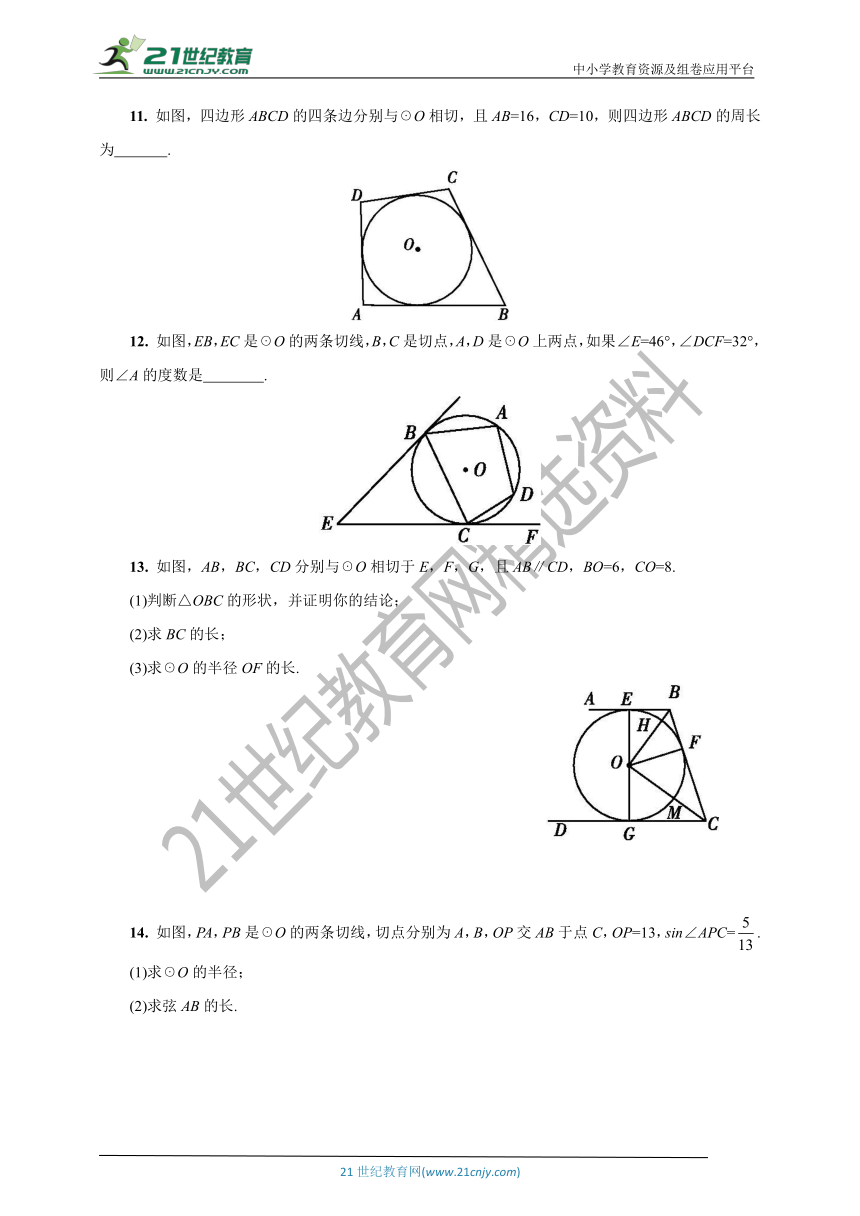
11. 如图,四边形ABCD的四条边分别与☉O相切,且AB=16,CD=10,则四边形ABCD的周长为 .?
12. 如图,EB,EC是☉O的两条切线,B,C是切点,A,D是☉O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是 .?
13. 如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求BC的长;
(3)求☉O的半径OF的长.
14. 如图,PA,PB是☉O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=.
(1)求☉O的半径;
(2)求弦AB的长.
15. 如图所示,AB是☉O的直径,延长AB到C,使BC=OB,过点C作☉O的切线CE,E为切点.
(1)求∠C的度数;
(2)过B点作☉O的切线交CE于F,交AE的延长线于D,请你判断△DEF的形状.
参 考 答 案
1. 3 60° 【解析】连接OA,因为PA,PB是☉O的切线,所以OA⊥PA,∠APO=∠BPO,在Rt△AOP中,OA=3,OP=6,所以∠APO=30°,PA===3,所以∠APB=2∠APO=60°.
2. 解:因为PA,PB分别与☉O相切于点A,B,所以PA=PB=4,因为过点C的切线分别交PA,PB于点D,E,所以DC=DA,EC=EB,所以△PED的周长为PD+DE+PE=PD+DC+CE+PE=PD+DA+EB+PE=PA+PB=4+4=8.
3. 6 cm 【解析】因为∠CAD=60°,所以∠CAB=120°,因为AB和AC与☉O相切,所以∠OAB=∠OAC,所以∠OAB=∠CAB=60°,因为AB=3 cm,所以OA=6 cm,所以由勾股定理得OB=3 cm,所以光盘的直径为6 cm.
4. 证明:连接EC.因为DC⊥AC,所以DC为☉O的切线.又因为DE为☉O的切线,所以DE=DC.所以∠DEC=∠DCE.因为AC为直径,所以∠CEA=90°,所以∠BED+∠DEC=90°.因为∠B+∠DCE=90°,所以∠B=∠BED,所以DB=DE.因为DE=DC,所以DB=DC,即D为BC的中点.
5. A 【解析】因为∠MPN=60°,所以∠OPM=30°.因为OP=50 cm,所以OM=25 cm.
6. D 【解析】因为AD,AB,BC是☉O的切线,所以EA=AD,BE=BC,所以AB+BC+CD+DA=AB+BE+AE+DC=2AB+DC=2×5+4=14.故选D.
7. C 【解析】因为PA,PB是☉O的切线,所以PA=PB,OA⊥PA,OB⊥PB,所以△PAB是等腰三角形,△PAO和△PBO是直角三角形,因为OA=OB,所以△AOB是等腰三角形,又因为∠APO=∠BPO,所以PO⊥AB,所以△AOC,△BOC,△APC,△BPC都是直角三角形.故选C.
8. D 【解析】设EC=x cm,则DE=(4-x) cm,由切线长定理得AF=AB=4 cm,EF=EC=x cm,所以在Rt△ADE中,(4+x)2=42+(4-x)2,解得x=1,所以DE=3 cm,所以S△ADE=×4×3=6(cm2).故选D.
9. B 【解析】连接OD,CD.因为AC为☉O的直径,所以∠ADC=90°,因为AD=,AC=3,所以CD=,因为OD=OC,所以∠OCD=∠ODC,因为DE是切线,所以∠CDE+∠ODC=90°.因为∠OCD+∠DCB=90°,所以∠BCD=∠CDE,所以DE=CE,由已知可得△ADC∽△ACB,所以=,所以BC==4,因为∠CDE+∠BDE=90°,∠DCB+∠B=90°,所以∠B=∠BDE,所以BE=DE,所以BE=CE=DE.所以DE=BC=×4=2.故选B.
10. A 【解析】因为PA,PB切☉O于A,B两点,CD切☉O于点E,所以PA=PB,AC=EC,DE=DB,因为△PCD的周长等于2,所以PA+PB=2,所以PA=PB=,连接PO,AO.因为☉O的半径为1,所以∠APO=30°,所以∠APB=60°,所以△APB是等边三角形,所以AB=PA=PB=,故选A.
11. 52 【解析】由切线长定理易证AB+CD=AD+BC,所以AB+BC+CD+AD=52.
12. 99° 【解析】因为EB,EC是☉O的切线,所以EB=EC,因为∠E=46°,所以∠ECB=∠EBC=67°,所以∠BCD=180°-(∠BCE+∠DCF)=81°;因为四边形ADCB内接于☉O,所以∠A+∠BCD=180°,所以∠A=180°-81°=99°.
13. 解:(1)△OBC是直角三角形. 证明:因为AB,BC,CD分别与☉O相切于E,F,G,所以∠OBE=∠OBF=∠EBF,∠OCG=∠OCF=∠GCF,因为AB∥CD,所以∠EBF+∠GCF=180°,所以∠OBF+∠OCF=90°,所以∠BOC=90°,所以△OBC是直角三角形.
(2)因为在Rt△BOC中,BO=6,CO=8,所以BC==10.
(3)因为AB,BC,CD分别与☉O相切于E,F,G,所以OF⊥BC,所以OF===4.8.
14. 解:(1)因为PA是☉O的切线,所以∠OAP=90°.因为sin∠APO==,OP=13,所以OA=5,即所求半径为5.
(2)在Rt△OAP中,AP===12.因为PA,PB是☉O的两条切线,所以PA=PB,∠APO=∠BPO,所以AC=BC=AB,PC⊥AB.在Rt△CAP中,sin∠APC==,所以AC=,所以AB=2AC=.
15. 解:(1)连接OE.因为BC=OB,所以OC=2OB=2OE.因为CE切☉O于点E,所以∠OEC=90°,所以∠C=30°.
(2)连接BE.因为FE,FB是☉O的切线,所以∠OEC=90°,∠ABF=90°,EF=FB,所以∠FEB=∠FBE.
因为∠C=30°,所以∠2=60°,所以∠3=60°,∠A=30°,所以∠FEB=30°,因为AB是直径,所以∠AEB=90°,∠DEB=90°,因为∠FEB=30°,所以∠1=60°.所以∠1+∠FEB=∠D+∠FBE=90°,所以∠D=∠1=60°,所以△DEF是等边三角形.
第24章 圆
24.4 直线与圆的位置关系
第3课时 切线长定理
要点测评 基础达标
要点1 切线长和切线长定理
1. 如图,☉O的半径是3,点P到圆心O的距离是6,PA,PB分别和☉O相切于点A,B,则切线长PA= ,∠APB的度数是 .?
2. 如图,P是☉O外的一点,PA,PB分别与☉O相切于点A,B,C是弧AB上的任意一点,过点C的切线分别交PA,PB于点D,E.若PA=4,求△PED的周长.
要点2 切线长定理的应用
3. 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3 cm,则此光盘的直径是 .?
4. 如图,在Rt△ABC中,∠C=90°,以AC为直径的☉O交AB于点E,DE为☉O的切线.
求证:D为BC的中点.
课后集训 巩固提升
5. 一个钢管放在V形架内,如图是其截面图,O为钢管的圆心.如果OP为50 cm,∠MPN=60°,则钢管的半径为( )
A. 25 cm B. 25 cm C. cm D. 50 cm
6. 如图所示,已知直角梯形ABCD,以腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E,若圆的半径为2,梯形的腰AB为5,则梯形ABCD的周长是( )
A. 9 B. 10 C. 12 D. 14
7. 如图所示,PA,PB是☉O的切线,A,B是切点,连接OP交AB于点C,连接OA,OB,则图中直角三角形和等腰三角形的个数分别为( )
A. 1,2 B. 2,2 C. 6,2 D. 6,1
8. 如图,正方形ABCD的边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积为( )
A. 12 cm2 B. 24 cm2 C. 8 cm2 D. 6 cm2
9. 如图,Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线,与边BC交于点E,若AD=,AC=3,则DE长为( )
A. B. 2 C. D.
10. 如图,PA,PB切☉O于A,B两点,CD切☉O于点E,交PA,PB于C,D.若☉O的半径为1,△PCD的周长等于2,则线段AB的长是( )
A. B. 3 C. 2 D. 3
11. 如图,四边形ABCD的四条边分别与☉O相切,且AB=16,CD=10,则四边形ABCD的周长为 .?
12. 如图,EB,EC是☉O的两条切线,B,C是切点,A,D是☉O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是 .?
13. 如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求BC的长;
(3)求☉O的半径OF的长.
14. 如图,PA,PB是☉O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=.
(1)求☉O的半径;
(2)求弦AB的长.
15. 如图所示,AB是☉O的直径,延长AB到C,使BC=OB,过点C作☉O的切线CE,E为切点.
(1)求∠C的度数;
(2)过B点作☉O的切线交CE于F,交AE的延长线于D,请你判断△DEF的形状.
参 考 答 案
1. 3 60° 【解析】连接OA,因为PA,PB是☉O的切线,所以OA⊥PA,∠APO=∠BPO,在Rt△AOP中,OA=3,OP=6,所以∠APO=30°,PA===3,所以∠APB=2∠APO=60°.
2. 解:因为PA,PB分别与☉O相切于点A,B,所以PA=PB=4,因为过点C的切线分别交PA,PB于点D,E,所以DC=DA,EC=EB,所以△PED的周长为PD+DE+PE=PD+DC+CE+PE=PD+DA+EB+PE=PA+PB=4+4=8.
3. 6 cm 【解析】因为∠CAD=60°,所以∠CAB=120°,因为AB和AC与☉O相切,所以∠OAB=∠OAC,所以∠OAB=∠CAB=60°,因为AB=3 cm,所以OA=6 cm,所以由勾股定理得OB=3 cm,所以光盘的直径为6 cm.
4. 证明:连接EC.因为DC⊥AC,所以DC为☉O的切线.又因为DE为☉O的切线,所以DE=DC.所以∠DEC=∠DCE.因为AC为直径,所以∠CEA=90°,所以∠BED+∠DEC=90°.因为∠B+∠DCE=90°,所以∠B=∠BED,所以DB=DE.因为DE=DC,所以DB=DC,即D为BC的中点.
5. A 【解析】因为∠MPN=60°,所以∠OPM=30°.因为OP=50 cm,所以OM=25 cm.
6. D 【解析】因为AD,AB,BC是☉O的切线,所以EA=AD,BE=BC,所以AB+BC+CD+DA=AB+BE+AE+DC=2AB+DC=2×5+4=14.故选D.
7. C 【解析】因为PA,PB是☉O的切线,所以PA=PB,OA⊥PA,OB⊥PB,所以△PAB是等腰三角形,△PAO和△PBO是直角三角形,因为OA=OB,所以△AOB是等腰三角形,又因为∠APO=∠BPO,所以PO⊥AB,所以△AOC,△BOC,△APC,△BPC都是直角三角形.故选C.
8. D 【解析】设EC=x cm,则DE=(4-x) cm,由切线长定理得AF=AB=4 cm,EF=EC=x cm,所以在Rt△ADE中,(4+x)2=42+(4-x)2,解得x=1,所以DE=3 cm,所以S△ADE=×4×3=6(cm2).故选D.
9. B 【解析】连接OD,CD.因为AC为☉O的直径,所以∠ADC=90°,因为AD=,AC=3,所以CD=,因为OD=OC,所以∠OCD=∠ODC,因为DE是切线,所以∠CDE+∠ODC=90°.因为∠OCD+∠DCB=90°,所以∠BCD=∠CDE,所以DE=CE,由已知可得△ADC∽△ACB,所以=,所以BC==4,因为∠CDE+∠BDE=90°,∠DCB+∠B=90°,所以∠B=∠BDE,所以BE=DE,所以BE=CE=DE.所以DE=BC=×4=2.故选B.
10. A 【解析】因为PA,PB切☉O于A,B两点,CD切☉O于点E,所以PA=PB,AC=EC,DE=DB,因为△PCD的周长等于2,所以PA+PB=2,所以PA=PB=,连接PO,AO.因为☉O的半径为1,所以∠APO=30°,所以∠APB=60°,所以△APB是等边三角形,所以AB=PA=PB=,故选A.
11. 52 【解析】由切线长定理易证AB+CD=AD+BC,所以AB+BC+CD+AD=52.
12. 99° 【解析】因为EB,EC是☉O的切线,所以EB=EC,因为∠E=46°,所以∠ECB=∠EBC=67°,所以∠BCD=180°-(∠BCE+∠DCF)=81°;因为四边形ADCB内接于☉O,所以∠A+∠BCD=180°,所以∠A=180°-81°=99°.
13. 解:(1)△OBC是直角三角形. 证明:因为AB,BC,CD分别与☉O相切于E,F,G,所以∠OBE=∠OBF=∠EBF,∠OCG=∠OCF=∠GCF,因为AB∥CD,所以∠EBF+∠GCF=180°,所以∠OBF+∠OCF=90°,所以∠BOC=90°,所以△OBC是直角三角形.
(2)因为在Rt△BOC中,BO=6,CO=8,所以BC==10.
(3)因为AB,BC,CD分别与☉O相切于E,F,G,所以OF⊥BC,所以OF===4.8.
14. 解:(1)因为PA是☉O的切线,所以∠OAP=90°.因为sin∠APO==,OP=13,所以OA=5,即所求半径为5.
(2)在Rt△OAP中,AP===12.因为PA,PB是☉O的两条切线,所以PA=PB,∠APO=∠BPO,所以AC=BC=AB,PC⊥AB.在Rt△CAP中,sin∠APC==,所以AC=,所以AB=2AC=.
15. 解:(1)连接OE.因为BC=OB,所以OC=2OB=2OE.因为CE切☉O于点E,所以∠OEC=90°,所以∠C=30°.
(2)连接BE.因为FE,FB是☉O的切线,所以∠OEC=90°,∠ABF=90°,EF=FB,所以∠FEB=∠FBE.
因为∠C=30°,所以∠2=60°,所以∠3=60°,∠A=30°,所以∠FEB=30°,因为AB是直径,所以∠AEB=90°,∠DEB=90°,因为∠FEB=30°,所以∠1=60°.所以∠1+∠FEB=∠D+∠FBE=90°,所以∠D=∠1=60°,所以△DEF是等边三角形.
