24.6 正多边形与圆(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.6 正多边形与圆(基础达标+巩固提升+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版数学九年级下册同步课时训练
第24章
圆
24.6 正多边形与圆
要点测评
基础达标
要点1 正多边形的概念
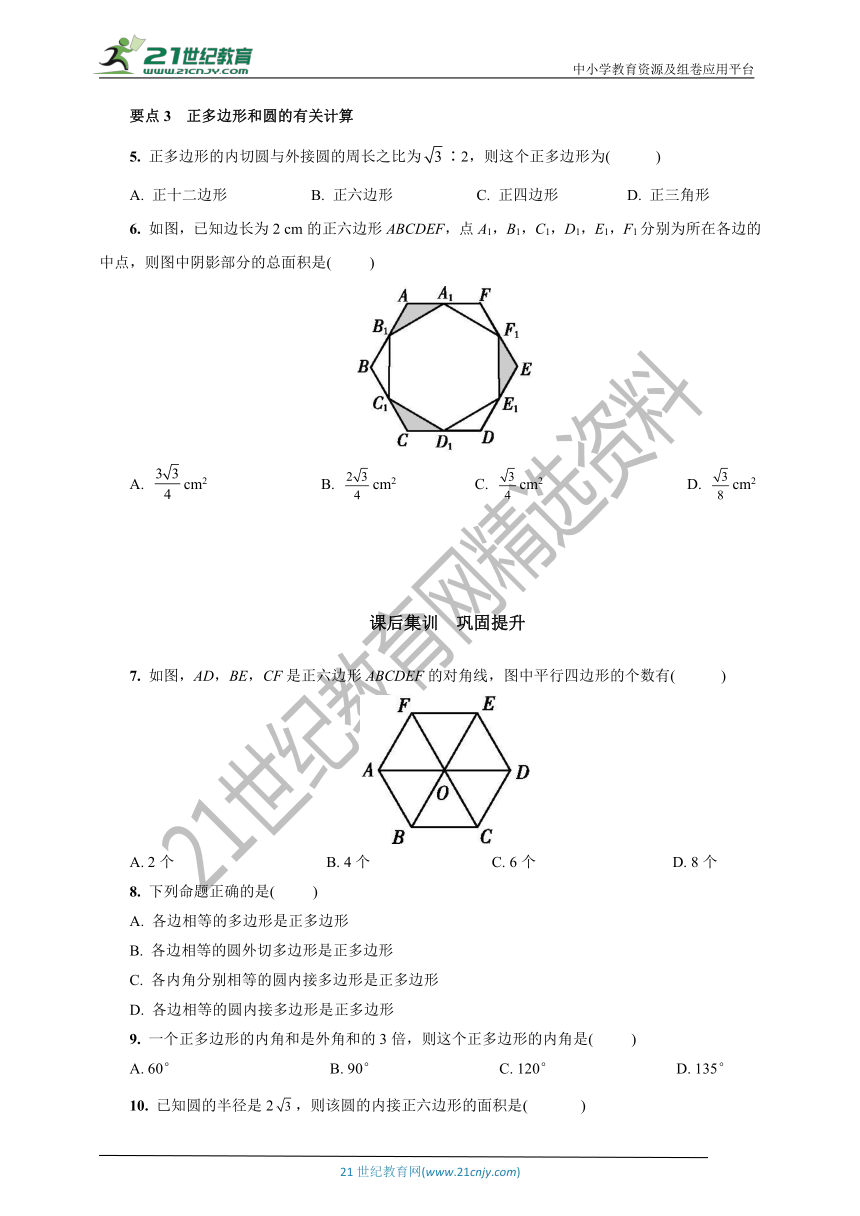
1.
若正六边形的半径为4,则它的边长等于(
)
A.
4
B.
2
C.
2
QUOTE
D.
4
QUOTE
2.
若一个正多边形的一个内角等于135°,那么这个多边形是正
边形.
要点2 正多边形和圆的关系
3.
五边形ABCDE中,∠A=∠B=∠C=∠D=∠E,AB,BC,CD,DE,EA与☉O相切,切点分别为A′,B′,C′,D′,E′,如图,
求证:五边形A′B′C′D′E′为正五边形.
4.
如图,已知☉O,用尺规作☉O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹)
要点3 正多边形和圆的有关计算
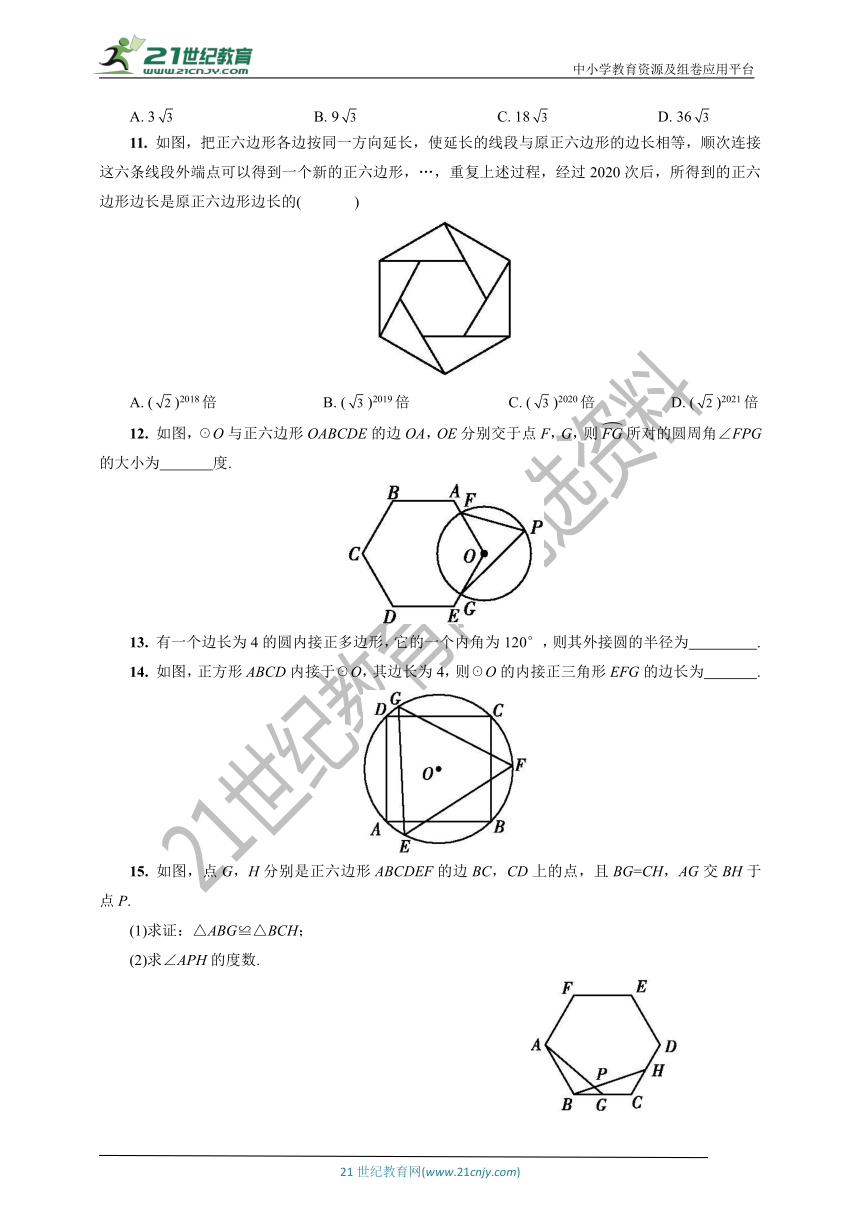
5.
正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为(
)
A.
正十二边形
B.
正六边形
C.
正四边形
D.
正三角形
6.
如图,已知边长为2
cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是(
)
A.
cm2
B.
cm2
C.
QUOTE
cm2
D.
cm2
课后集训
巩固提升
7.
如图,AD,BE,CF是正六边形ABCDEF的对角线,图中平行四边形的个数有(
)
A.
2个
B.
4个
C.
6个
D.
8个
8.
下列命题正确的是(
)
A.
各边相等的多边形是正多边形
B.
各边相等的圆外切多边形是正多边形
C.
各内角分别相等的圆内接多边形是正多边形
D.
各边相等的圆内接多边形是正多边形
9.
一个正多边形的内角和是外角和的3倍,则这个正多边形的内角是(
)
A.
60°
B.
90°
C.
120°
D.
135°
10.
已知圆的半径是2
QUOTE
,则该圆的内接正六边形的面积是(
)
A.
3
QUOTE
B.
9
QUOTE
C.
18
QUOTE
D.
36
QUOTE
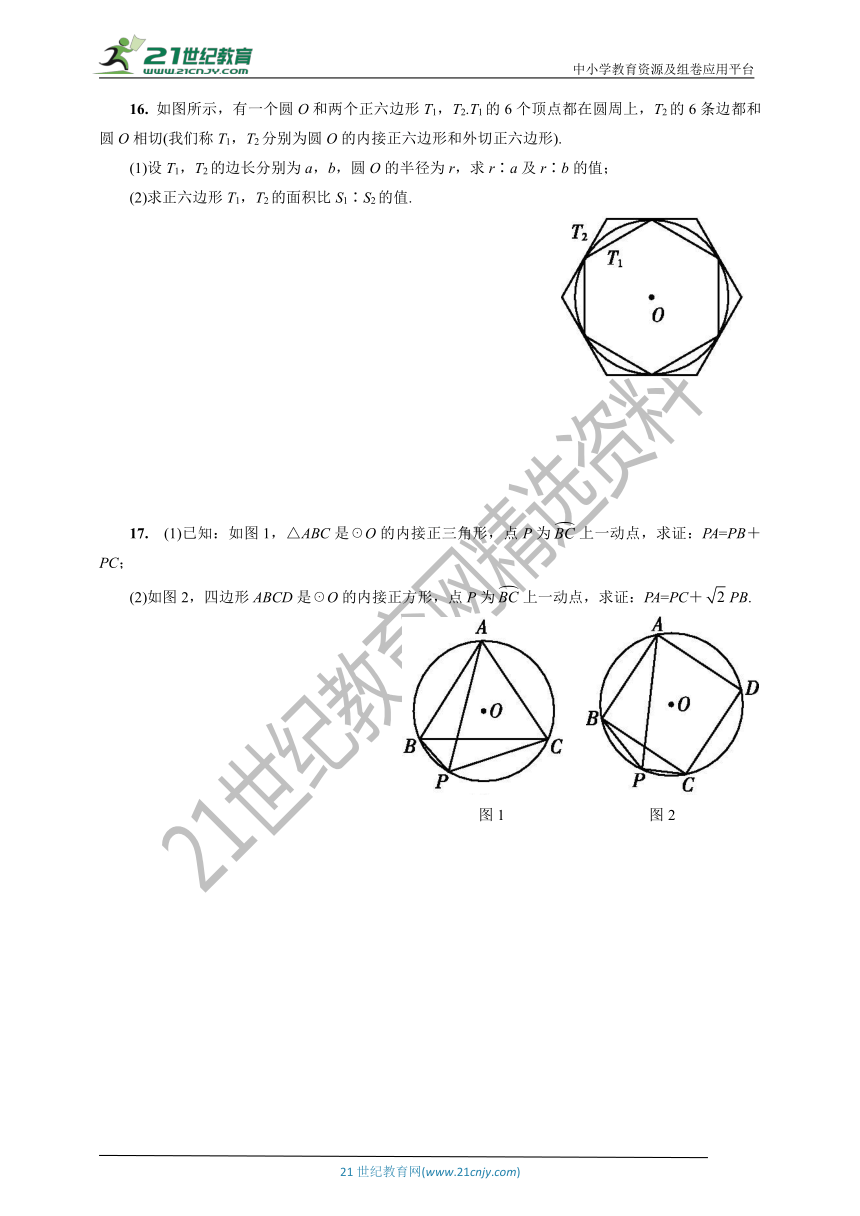
11.
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2020次后,所得到的正六边形边长是原正六边形边长的(
)
A.
(
QUOTE
)2018倍
B.
(
QUOTE
)2019倍
C.
(
QUOTE
)2020倍
D.
(
QUOTE
)2021倍
12.
如图,☉O与正六边形OABCDE的边OA,OE分别交于点F,G,则所对的圆周角∠FPG的大小为
度.
13.
有一个边长为4的圆内接正多边形,它的一个内角为120°,则其外接圆的半径为
.
14.
如图,正方形ABCD内接于☉O,其边长为4,则☉O的内接正三角形EFG的边长为
.
15.
如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
16.
如图所示,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r∶a及r∶b的值;
(2)求正六边形T1,T2的面积比S1∶S2的值.
17.
(1)已知:如图1,△ABC是☉O的内接正三角形,点P为上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是☉O的内接正方形,点P为上一动点,求证:PA=PC+PB.
图1
图2
参
考
答
案
1.
A 【解析】正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边组成一个等边三角形,故正六边形的边长是4.故选A.
2.
八 【解析】设正多边形的边数为n,则有(n-2)·180°=135°·n,所以n=8.
3.
证明:连接OA′,OB′,OC′,则OA′⊥AB,OB′⊥BC,OC′⊥CD,所以∠B+∠1=180°,∠C+∠2=180°.又因为∠B=∠C,所以∠1=∠2.所以=,同理===,即切点A′,B′,C′,D′,E′是☉O的五等分点,所以五边形A′B′C′D′E′为正五边形.
4.
解:如图所示,四边形ABCD即为所求.
(提示:画圆的一条直径AC,作这条直径的中垂线交☉O于点B,D)
5.
B 【解析】正多边形的内切圆与外接圆的周长之比为∶2,则半径之比为∶2,设AB是正多边形的一边,作OC⊥AB,则OC=a,OA=OB=2a,在直角△AOC中,cos∠AOC==,所以∠AOC=30°,所以∠AOB=60°,则正多边形边数是=6.故选B.
6.
A 【解析】边长是2
cm的正六边形ABCDEF的面积是6××sin
60°×22=6
cm2.作出中心O,连接OD1,OC,OC与C1D1交于点G,在Rt△OCD1中,∠O=30°,CD1=CD=1(cm).则OD1=CD1=
cm,D1G=OD1=
cm,C1D1=
cm.则正六边形A1B1C1D1E1F1的面积是6××sin
60°×()2=
cm2.则图中阴影部分的总面积是(6-)=
cm2.故选A.
7.
C 【解析】因为AD,BE,CF是正六边形ABCDEF的对角线,所以OA=OE=AF=EF,所以四边形AOEF是平行四边形,同理:四边形DEFO,四边形ABCO,四边形BCDO,四边形CDEO,四边形FABO都是平行四边形,共6个,故选C.
8.
D 【解析】菱形各边相等,但不是正多边形,故选项A错误;菱形也有内切圆,故选项B错误;长方形有外接圆,但不是正多边形,故选项C错误;各边相等的圆内接多边形由弦相等可知所对的弧相等,可得各内角也相等,据正多边形的定义知选项D正确.故选D.
9.
D 【解析】设正多边形有n条边,则有(n-2)·180°=3×360°,所以n=8,所以每个内角是=135°.故选D.
10.
C 【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,所以正六边形的面积为18,故选C.
11.
C 【解析】因为此六边形是正六边形,所以∠1=180°-120°=60°,因为BD=CD=BC=AD,所以△BCD为等边三角形,所以BD=AC,所以△ABC是直角三角形,因为BC=AC,所以∠2=30°,所以AB=BC=CD,同理可得,经过2次后,所得到的正六边形是原正六边形边长的()2倍,所以经过2020次后,所得到的正六边形是原正六边形边长的()2020倍,故选C.
12.
60 【解析】因为多边形OABCDE是正六边形,所以∠AOE=120°,所以∠FPG=60°.
13.
4 【解析】内角为120°的正多边形是正六边形,其外接圆半径与边长相等.
14.
2 【解析】连接AC,OE,OF,作OM⊥EF于M,因为四边形ABCD是正方形,所以AB=BC=4,∠ABC=90°,所以AC是直径,AC=4,所以OE=OF=2,因为OM⊥EF,所以EM=MF,因为△EFG是等边三角形,所以∠GEF=60°,在Rt△OME中,因为OE=2,∠OEM=∠GEF=30°,所以OM=,EM=OM=,所以EF=2.
15.
(1)证明:因为在正六边形ABCDEF中,AB=BC,∠ABC=∠C=120°,在△ABG与△BCH中,所以△ABG≌△BCH.
(2)解:由(1)知:△ABG≌△BCH,所以∠BAG=∠HBC,所以∠BPG=∠ABG=120°,所以∠APH=∠BPG=120°.
16.
解:(1)连接圆心O和T1的六个顶点可得到6个全等的正三角形,所以r∶a=1∶1.连接圆心O和T2相邻的两个顶点得到以圆O的半径为高的正三角形,所以r∶b=∶2.
(2)因为由(1)知T1与T2的边长之比为∶2,所以S1∶S2=()2=3∶4.
17.
证明:(1)如图1,延长BP至E,使PE=PC,连接CE.因为A,B,P,C四点共圆,所以∠BAC=∠CPE=60°,因为PE=PC,所以△PCE是等边三角形,所以CE=PC,∠E=60°;又因为∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,所以∠BCE=∠ACP,又因为CE=PC,AC=BC,所以△BEC≌△APC(SAS),所以PA=BE=PB+PC.
(2)如图2,过点B作BE⊥PB交PA于E.因为∠1+∠2=∠2+∠3=90°,所以∠1=∠3,易得∠APB=45°,所以BP=BE,所以PE=PB;又因为AB=BC,所以△ABE≌△CBP(SAS),所以PC=AE.所以PA=AE+PE=PC+PB.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
沪科版数学九年级下册同步课时训练
第24章
圆
24.6 正多边形与圆
要点测评
基础达标
要点1 正多边形的概念
1.
若正六边形的半径为4,则它的边长等于(
)
A.
4
B.
2
C.
2
QUOTE
D.
4
QUOTE
2.
若一个正多边形的一个内角等于135°,那么这个多边形是正
边形.
要点2 正多边形和圆的关系
3.
五边形ABCDE中,∠A=∠B=∠C=∠D=∠E,AB,BC,CD,DE,EA与☉O相切,切点分别为A′,B′,C′,D′,E′,如图,
求证:五边形A′B′C′D′E′为正五边形.
4.
如图,已知☉O,用尺规作☉O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹)
要点3 正多边形和圆的有关计算
5.
正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为(
)
A.
正十二边形
B.
正六边形
C.
正四边形
D.
正三角形
6.
如图,已知边长为2
cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是(
)
A.
cm2
B.
cm2
C.
QUOTE
cm2
D.
cm2
课后集训
巩固提升
7.
如图,AD,BE,CF是正六边形ABCDEF的对角线,图中平行四边形的个数有(
)
A.
2个
B.
4个
C.
6个
D.
8个
8.
下列命题正确的是(
)
A.
各边相等的多边形是正多边形
B.
各边相等的圆外切多边形是正多边形
C.
各内角分别相等的圆内接多边形是正多边形
D.
各边相等的圆内接多边形是正多边形
9.
一个正多边形的内角和是外角和的3倍,则这个正多边形的内角是(
)
A.
60°
B.
90°
C.
120°
D.
135°
10.
已知圆的半径是2
QUOTE
,则该圆的内接正六边形的面积是(
)
A.
3
QUOTE
B.
9
QUOTE
C.
18
QUOTE
D.
36
QUOTE
11.
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2020次后,所得到的正六边形边长是原正六边形边长的(
)
A.
(
QUOTE
)2018倍
B.
(
QUOTE
)2019倍
C.
(
QUOTE
)2020倍
D.
(
QUOTE
)2021倍
12.
如图,☉O与正六边形OABCDE的边OA,OE分别交于点F,G,则所对的圆周角∠FPG的大小为
度.
13.
有一个边长为4的圆内接正多边形,它的一个内角为120°,则其外接圆的半径为
.
14.
如图,正方形ABCD内接于☉O,其边长为4,则☉O的内接正三角形EFG的边长为
.
15.
如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
16.
如图所示,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r∶a及r∶b的值;
(2)求正六边形T1,T2的面积比S1∶S2的值.
17.
(1)已知:如图1,△ABC是☉O的内接正三角形,点P为上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是☉O的内接正方形,点P为上一动点,求证:PA=PC+PB.
图1
图2
参
考
答
案
1.
A 【解析】正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边组成一个等边三角形,故正六边形的边长是4.故选A.
2.
八 【解析】设正多边形的边数为n,则有(n-2)·180°=135°·n,所以n=8.
3.
证明:连接OA′,OB′,OC′,则OA′⊥AB,OB′⊥BC,OC′⊥CD,所以∠B+∠1=180°,∠C+∠2=180°.又因为∠B=∠C,所以∠1=∠2.所以=,同理===,即切点A′,B′,C′,D′,E′是☉O的五等分点,所以五边形A′B′C′D′E′为正五边形.
4.
解:如图所示,四边形ABCD即为所求.
(提示:画圆的一条直径AC,作这条直径的中垂线交☉O于点B,D)
5.
B 【解析】正多边形的内切圆与外接圆的周长之比为∶2,则半径之比为∶2,设AB是正多边形的一边,作OC⊥AB,则OC=a,OA=OB=2a,在直角△AOC中,cos∠AOC==,所以∠AOC=30°,所以∠AOB=60°,则正多边形边数是=6.故选B.
6.
A 【解析】边长是2
cm的正六边形ABCDEF的面积是6××sin
60°×22=6
cm2.作出中心O,连接OD1,OC,OC与C1D1交于点G,在Rt△OCD1中,∠O=30°,CD1=CD=1(cm).则OD1=CD1=
cm,D1G=OD1=
cm,C1D1=
cm.则正六边形A1B1C1D1E1F1的面积是6××sin
60°×()2=
cm2.则图中阴影部分的总面积是(6-)=
cm2.故选A.
7.
C 【解析】因为AD,BE,CF是正六边形ABCDEF的对角线,所以OA=OE=AF=EF,所以四边形AOEF是平行四边形,同理:四边形DEFO,四边形ABCO,四边形BCDO,四边形CDEO,四边形FABO都是平行四边形,共6个,故选C.
8.
D 【解析】菱形各边相等,但不是正多边形,故选项A错误;菱形也有内切圆,故选项B错误;长方形有外接圆,但不是正多边形,故选项C错误;各边相等的圆内接多边形由弦相等可知所对的弧相等,可得各内角也相等,据正多边形的定义知选项D正确.故选D.
9.
D 【解析】设正多边形有n条边,则有(n-2)·180°=3×360°,所以n=8,所以每个内角是=135°.故选D.
10.
C 【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,所以正六边形的面积为18,故选C.
11.
C 【解析】因为此六边形是正六边形,所以∠1=180°-120°=60°,因为BD=CD=BC=AD,所以△BCD为等边三角形,所以BD=AC,所以△ABC是直角三角形,因为BC=AC,所以∠2=30°,所以AB=BC=CD,同理可得,经过2次后,所得到的正六边形是原正六边形边长的()2倍,所以经过2020次后,所得到的正六边形是原正六边形边长的()2020倍,故选C.
12.
60 【解析】因为多边形OABCDE是正六边形,所以∠AOE=120°,所以∠FPG=60°.
13.
4 【解析】内角为120°的正多边形是正六边形,其外接圆半径与边长相等.
14.
2 【解析】连接AC,OE,OF,作OM⊥EF于M,因为四边形ABCD是正方形,所以AB=BC=4,∠ABC=90°,所以AC是直径,AC=4,所以OE=OF=2,因为OM⊥EF,所以EM=MF,因为△EFG是等边三角形,所以∠GEF=60°,在Rt△OME中,因为OE=2,∠OEM=∠GEF=30°,所以OM=,EM=OM=,所以EF=2.
15.
(1)证明:因为在正六边形ABCDEF中,AB=BC,∠ABC=∠C=120°,在△ABG与△BCH中,所以△ABG≌△BCH.
(2)解:由(1)知:△ABG≌△BCH,所以∠BAG=∠HBC,所以∠BPG=∠ABG=120°,所以∠APH=∠BPG=120°.
16.
解:(1)连接圆心O和T1的六个顶点可得到6个全等的正三角形,所以r∶a=1∶1.连接圆心O和T2相邻的两个顶点得到以圆O的半径为高的正三角形,所以r∶b=∶2.
(2)因为由(1)知T1与T2的边长之比为∶2,所以S1∶S2=()2=3∶4.
17.
证明:(1)如图1,延长BP至E,使PE=PC,连接CE.因为A,B,P,C四点共圆,所以∠BAC=∠CPE=60°,因为PE=PC,所以△PCE是等边三角形,所以CE=PC,∠E=60°;又因为∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,所以∠BCE=∠ACP,又因为CE=PC,AC=BC,所以△BEC≌△APC(SAS),所以PA=BE=PB+PC.
(2)如图2,过点B作BE⊥PB交PA于E.因为∠1+∠2=∠2+∠3=90°,所以∠1=∠3,易得∠APB=45°,所以BP=BE,所以PE=PB;又因为AB=BC,所以△ABE≌△CBP(SAS),所以PC=AE.所以PA=AE+PE=PC+PB.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
