江苏省无锡市2019-2020学年度第一学期苏科版七年级上数学期末数、式、方程的专题复习学案(含答案)
文档属性
| 名称 | 江苏省无锡市2019-2020学年度第一学期苏科版七年级上数学期末数、式、方程的专题复习学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 64.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 20:16:41 | ||
图片预览



文档简介
初一数学数、式、方程的专题复习
【学习目标】
复习本学期所学的有理数、代数式、一元一次方程的相关知识,感受“数形结合”、“分类”、“转化”、“模型”的思想.
【典型例题】
题型一、有理数相关概念的识别
例题1.对某校九年级男生进行引体向上测试,以能做7个为标准,超过7个用正数表示,不足7个用负数表示,其中8名男生的成绩如下(单位:个):2,-1,0,3,-2,-3,1,0.问:
(1)这8名男生有几名达标? (2)达标的百分率是多少?
例题2.把下列各数填入相应的括号内:
,0,,0.211,-,,,-0.5,8,1.1212212221…(两个1之间依次多一个2)
正数集合:{ …};
非负整数集合:{ …};
有理数集合:{ …};
无理数集合:{ …}.
例题3.到数轴上距离表示数1的点有3个单位长度的数是________.
【变式1】比较大小.
(1)-1与-0.01:__________________; (2)-|-2|与0:________________;
(3)-0.3与-:________________; (4)-与:______________.
【变式2】数轴上表示整数的点称为整点,某数轴的单位长度是1cm,若在数轴上随意画出一条长1000cm 的线段AB,则线段AB盖住的整点的个数是( )
A. 998或999 B. 999或1000 C.1000或1001 D.1001或1002
例题4.若|x|=5,则x=________;若|x|=|-3|,则x=________.
【变式1】若| a+2 |+|b—3|=0,则| a |+| b |=________.
【变式2】有理数a、b、c在数轴上的位置如图所示.
将a、-a、b、-b、c、-c、0按从小到大的顺序用“<”连接起来.
题型二、 有理数的运算
例题5.计算:①-2.8-6.2+(-3.4)-(-5.6) ② (-1)×(+)×(-8)-9÷(-1)2
③(-2)3-32-(-2)2+ (-3)3 ④ (-60)×÷4
【变式1】(易错题)计算:①(-32)÷4×(-8); ②÷(-).
【变式2】(技巧类计算)
(逆用运算法)计算: (-5)×(-3)+(-7) ×(-3)-9×(-3)
(拆项相消法)计算: +++++
题型三、 代数式的相关概念
例题6.填空
①单项式-vt的系数是________,次数是________,是______次单项式.
②多项式2x+3y2-3xy2是单项式_______,_______,_______的和,一次项是________.
③若-xm+2yn+1和-5x6y4是同类项,则m=_______,n=________.
④合并下列多项式中的同类项:-xy-(4z-2xy)-(3xy-4z)=_____________________.
题型四、整体、转化思想求代数式的值
例题7.①已知a+b=-5,ab=7,求a2b+ab2-a-b的值.
②已知x=y-3,求(x-y)2+(x-y)-(x-y)2+(x-y)+3的值.
题型五、整式的加减
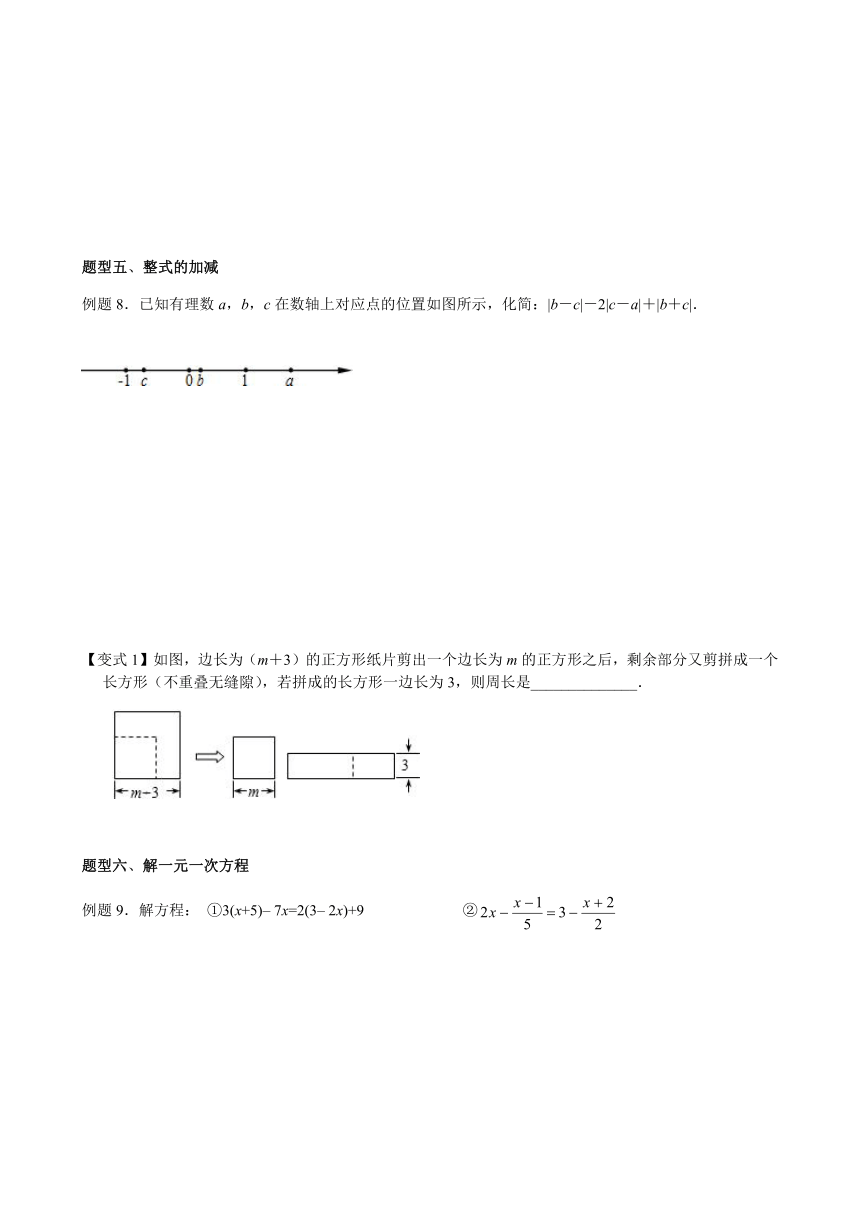
例题8.已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c-a|+|b+c|.
【变式1】如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则周长是______________.
题型六、解一元一次方程
例题9.解方程: ①3(x+5)– 7x=2(3– 2x)+9 ②
【变式1】已知关于x的方程9x-3=kx+14有整数解,求满足条件的所有整数k.
题型七、用一元一次方程解决问题
例题10.轮船从甲地顺流而行9小时到达乙地,原路返回11小时才能到达甲地,已知水流速度为2千米/时,求轮船在静水中的速度及甲、乙两地的距离.
【变式1】一件工程,甲单独做需要8天完成,乙单独做需要5天完成,丙单独做需要20天完成.甲、乙合作2天后,乙因有事离开,由甲、丙继续合作,还需要几天完成?
【变式2】全班同学去划船,如果减少一条船,那么每条船正好坐9名同学,如果增加一条船,那么每条船正好坐6名同学,问这个班共有多少名同学?
【课后练习】
1.“十一”黄金周期间无锡市共接待游客约5349000人,该数据用科学记数法表示为
( )
A.5349×103 B.5.349×103 C.5.349×106 D.5.349×107
2.国庆期间,某商店推出全店打8折的优惠活动,持贵宾卡的客户还可在8折的基础
上再打9折.某人持贵宾卡买了一件商品共花了a元,则该商品的标价是( )
A.元 B.元 C.元 D.元
3.如图,小惠设计了一个电脑程序,已知x、y为两个不相等的有理数,当输出的值
M=24时,所输入的x、y中较大的数为( )
A.48 B.24 C.12 D.6
4.如图所示,阴影部分的面积为 .
5.如果方程(m-2)x|m|-1+8=0是关于x的一元一次方程,则m= .
6.对有理数a、b规定运算★如下:a★b=,则—2★—4=_________.
7.解方程:
(1) x+2=12-4x; (2) 4-(2-x)=5x; (3) -=1.
8.有理数a、b、c在数轴上的位置如图所示:
(1)判断正负,用“>”或“<”填空:b -1; a 1;c b. (2)化简:|b+1|+|a-1|-|c-b|.
9.某水果批发商欲将A市的一批水果运往B市销售,有火车和汽车两种运输工具,运输过程中的损耗均为160元/时.其它主要参考数据如下:
运输工具 平均速度(千米/时) 运费(元/千米) 装卸费用(元)
火车 100 18 1800
汽车 80 22 1000
(1)若汽车的总支出费用比火车费用多960元,求A市与B市之间的路程;
(2)若A市与C市之间的距离为S千米,要想将这批水果运往C市销售.选择哪种运输工具比较合算,说明你的理由.
10.如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
(1)用含有t的代数式表示AM的长为_______________.
(2)当t=_______秒时,AM+BN=11.
(3)若点A、B与线段MN同时移动,点A以每秒2个单位的速度向数轴的正方向移动,点B以每秒1个单位的速度向数轴的负方向移动,在移动过程中,AM和BN可能相等吗?若相等,请求出t的值,若不相等,请说明理由.
数、式、方程的专题复习
课后练习答案:
1.C
2.D
3.C
4.mn?
5.-2
6.4
7.(1)5x=10,x=2
(2)4-2+x=5x,4x=2,x=
(3)3x-2(5+ x)=6,3x-10-2 x=6,x=16
8.(1) <;<;>.
(2)原式=(-b-1)+(-a+1)-(c-b)
=-b-1-a+1-c+b
=-a-c
9.(1)设A市与B市的路程为x千米,依题意得:160×+18x+1800+960=160×+22x+1000,
解得:x=400,
答:A市与B市之间路程400千米;
(2)火车运输费用为:160×+18s+1800,汽车运输费用为:160×+22s+1000,费用相等时可以解得
s=,所以当A市与C市的距离大于千米时,选择火车运输较合算;当A市与C市的距离等于千米时,选择火车和汽车两种方式运输均可;当A市与C市的距离小于千米时,选择汽车运输较合算.
10.解:(1)∵点A、M、N对应的数字分别为?1、0、2,线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒,∴移动后M表示的数为t,N表示的数为t+2,
∴AM=t? (?1)=t+1.
(2)由(1)可知:BM=︱11? (t+2)︱=︱9?t︱,
∵AM+BN=11
∴t+1+︱9? t︱=11 解得:t=
(3)假设能相等,则点A表示的数为2t?1,M表示的数为t,N表示的数为t+2,B表示的数为11?t,
∴AM=︱2t?1?t︱=︱t?1︱,BN=︱t+2?(11? t)︱=︱2 t?9︱
∵AM=BN
∴︱t?1︱=︱2 t?9︱
解得:=,=8,故在运动的过程中AM和BN能相等,此时运动的时间为秒和8秒.
(第4题)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
