2019秋湘教版九年级数学上册第一章反比例函数单元测试含答案
文档属性
| 名称 | 2019秋湘教版九年级数学上册第一章反比例函数单元测试含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 516.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 10:11:52 | ||
图片预览

文档简介
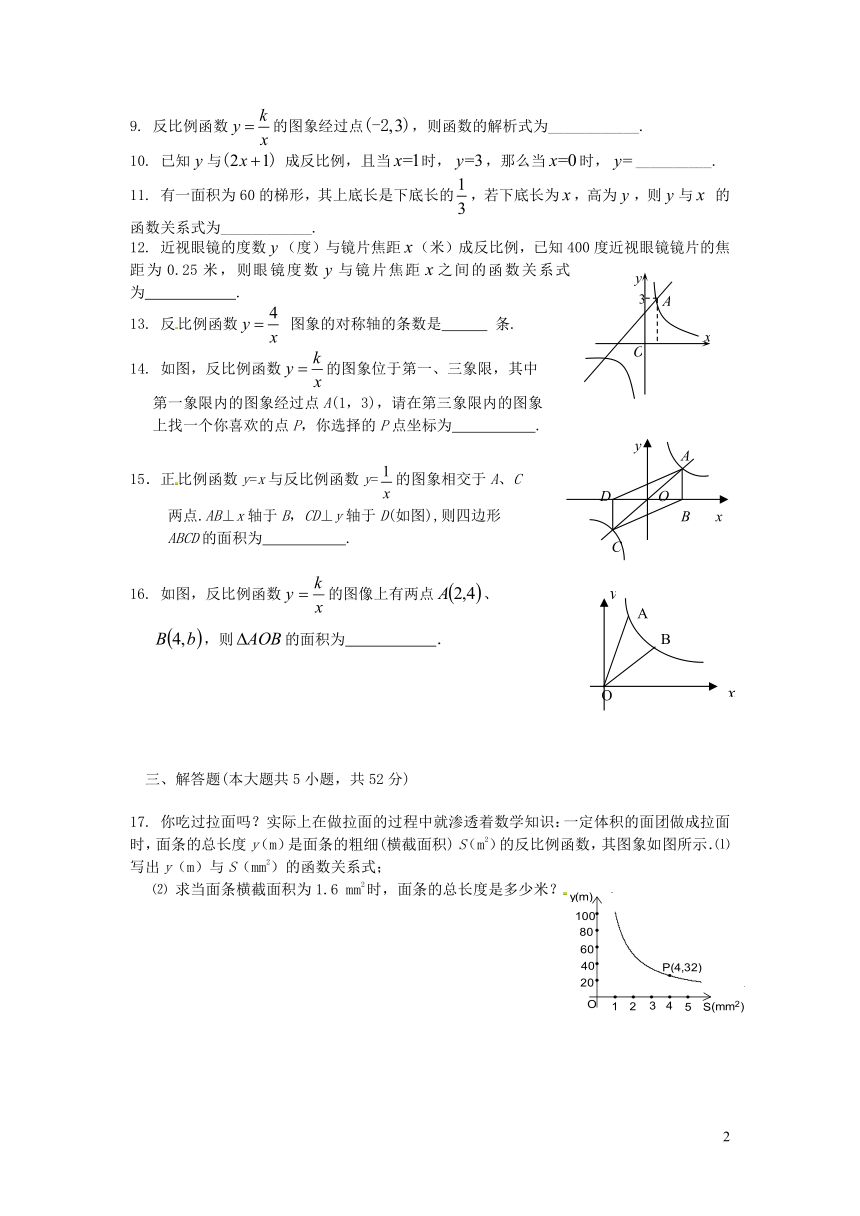
2019秋湘教版九年级数学上册第一章反比例函数周测4全章学案设计
选择题(本题共8小题,每小题3分,共24分)
1. 下列各点中,在反比例函数 图象上的是( )
A. B. C. D.
2. 已知函数的图象过点,则该函数的图象必在( )
A. 第二、三象限 B. 第二、四象限 C. 第一、三象限 D. 第三、四象限
3. 若函数的图象在其象限内的值随值的增大而增大,则的取值范围
是( )
A. B. C. D.
4. 已知三角形的面积一定,则底边与其上的高之间的函数关系的图象大致是( )
A B C D
5. 反比例函数图象上有三个点,其中,则的大小关系是 ( )
A. B.
C. D.
6. 若,则正比例函数与反比例函数在同一坐标系中的大致图象可能是( )
7. 如图,函数和函数的图象相交于点
, ,若,则x的取值范围是( )
A. B.
C. D.
二、填空题(本题共8小题,每小题3分,共24分)
9. 反比例函数的图象经过点,则函数的解析式为____________.
10. 已知与 成反比例,且当时,,那么当时,__________.
11. 有一面积为60的梯形,其上底长是下底长的,若下底长为,高为,则与 的函数关系式为____________.
12. 近视眼镜的度数(度)与镜片焦距(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数与镜片焦距之间的函数关系式为 .
13. 反比例函数 图象的对称轴的条数是 条.
14. 如图,反比例函数的图象位于第一、三象限,其中
第一象限内的图象经过点A(1,3),请在第三象限内的图象
上找一个你喜欢的点P,你选择的P点坐标为 .
15.正比例函数y=x与反比例函数y=的图象相交于A、C
两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形
ABCD的面积为 .
16. 如图,反比例函数的图像上有两点、
,则的面积为 .
三、解答题(本大题共5小题,共52分)
17. 你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面时,面条的总长度y(m)是面条的粗细(横截面积) S(m2)的反比例函数,其图象如图所示.⑴ 写出y(m)与S(mm2)的函数关系式;
⑵ 求当面条横截面积为1.6 mm2时,面条的总长度是多少米?
18. 如图,在平面直角坐标系中,反比例函数的图象与一次函数 的图象的一个交点为.
(1)求这个一次函数的解析式;
(2)若是轴上一点,且满足, 求点的坐标.
19. 如图,在平面直角坐标系xOy中,正比例函数与反比例函数的图象在第二象限交于点A,且点A的横坐标为-2.
(1) 求反比例函数的解析式;
(2)点B的坐标为(-3,0),若点P在y轴上,且△AOB的面积
与△AOP的面积相等,直接写出点P的坐标.
20.一次函数的图像与反比例函数的图像交于、
两点.(1)求反比例函数和一次函数的解析式;
(2)根据图像写出使反比例函数值大于一次函数值的取值范围.
21. 如图,一次函数的图象与反比例函数的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的
面积相等?若存在,给出证明并求出点P的坐标;
若不存在,说明理由.
参考答案
一、选择题:1.A; 2. B; 3.B; 4.D; 5.C;6. B;7.D;8.C
二、填空题:9. ; 10. 9; 11. ; 12. ;
13. ; 14. 答案不唯一, 、满足,且、即可;
15. 2; 16. 6
三、解答题:
17. (1) (2)
18. (1)∵ 点在反比例函数的图象上,∴ .
∴ 点的坐标为.
∵ 点在一次函数的图象上, ∴. ∴.
∴ 一次函数的解析式为.
(2)点的坐标为(-3,0)或(1,0).
19. (1)∵正比例函数的图象经过点A,且点A的横坐标为,
∴点A的纵坐标为3.
∵反比例函数的图象经过点A(), ∴.
∴. ∴.
(2)点P的坐标为或.
20. (1),; (2)或.
21. (1) (2)
(3)存在. 利用点C、D关于直线对称. 或.
.
选择题(本题共8小题,每小题3分,共24分)
1. 下列各点中,在反比例函数 图象上的是( )
A. B. C. D.
2. 已知函数的图象过点,则该函数的图象必在( )
A. 第二、三象限 B. 第二、四象限 C. 第一、三象限 D. 第三、四象限
3. 若函数的图象在其象限内的值随值的增大而增大,则的取值范围
是( )
A. B. C. D.
4. 已知三角形的面积一定,则底边与其上的高之间的函数关系的图象大致是( )
A B C D
5. 反比例函数图象上有三个点,其中,则的大小关系是 ( )
A. B.
C. D.
6. 若,则正比例函数与反比例函数在同一坐标系中的大致图象可能是( )
7. 如图,函数和函数的图象相交于点
, ,若,则x的取值范围是( )
A. B.
C. D.
二、填空题(本题共8小题,每小题3分,共24分)
9. 反比例函数的图象经过点,则函数的解析式为____________.
10. 已知与 成反比例,且当时,,那么当时,__________.
11. 有一面积为60的梯形,其上底长是下底长的,若下底长为,高为,则与 的函数关系式为____________.
12. 近视眼镜的度数(度)与镜片焦距(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数与镜片焦距之间的函数关系式为 .
13. 反比例函数 图象的对称轴的条数是 条.
14. 如图,反比例函数的图象位于第一、三象限,其中
第一象限内的图象经过点A(1,3),请在第三象限内的图象
上找一个你喜欢的点P,你选择的P点坐标为 .
15.正比例函数y=x与反比例函数y=的图象相交于A、C
两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形
ABCD的面积为 .
16. 如图,反比例函数的图像上有两点、
,则的面积为 .
三、解答题(本大题共5小题,共52分)
17. 你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面时,面条的总长度y(m)是面条的粗细(横截面积) S(m2)的反比例函数,其图象如图所示.⑴ 写出y(m)与S(mm2)的函数关系式;
⑵ 求当面条横截面积为1.6 mm2时,面条的总长度是多少米?
18. 如图,在平面直角坐标系中,反比例函数的图象与一次函数 的图象的一个交点为.
(1)求这个一次函数的解析式;
(2)若是轴上一点,且满足, 求点的坐标.
19. 如图,在平面直角坐标系xOy中,正比例函数与反比例函数的图象在第二象限交于点A,且点A的横坐标为-2.
(1) 求反比例函数的解析式;
(2)点B的坐标为(-3,0),若点P在y轴上,且△AOB的面积
与△AOP的面积相等,直接写出点P的坐标.
20.一次函数的图像与反比例函数的图像交于、
两点.(1)求反比例函数和一次函数的解析式;
(2)根据图像写出使反比例函数值大于一次函数值的取值范围.
21. 如图,一次函数的图象与反比例函数的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的
面积相等?若存在,给出证明并求出点P的坐标;
若不存在,说明理由.
参考答案
一、选择题:1.A; 2. B; 3.B; 4.D; 5.C;6. B;7.D;8.C
二、填空题:9. ; 10. 9; 11. ; 12. ;
13. ; 14. 答案不唯一, 、满足,且、即可;
15. 2; 16. 6
三、解答题:
17. (1) (2)
18. (1)∵ 点在反比例函数的图象上,∴ .
∴ 点的坐标为.
∵ 点在一次函数的图象上, ∴. ∴.
∴ 一次函数的解析式为.
(2)点的坐标为(-3,0)或(1,0).
19. (1)∵正比例函数的图象经过点A,且点A的横坐标为,
∴点A的纵坐标为3.
∵反比例函数的图象经过点A(), ∴.
∴. ∴.
(2)点P的坐标为或.
20. (1),; (2)或.
21. (1) (2)
(3)存在. 利用点C、D关于直线对称. 或.
.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
