人教版九年级数学下册28.1锐角三角函数-余弦、正切课件(第二课时 共22张PPT)
文档属性
| 名称 | 人教版九年级数学下册28.1锐角三角函数-余弦、正切课件(第二课时 共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
数学九年级下册
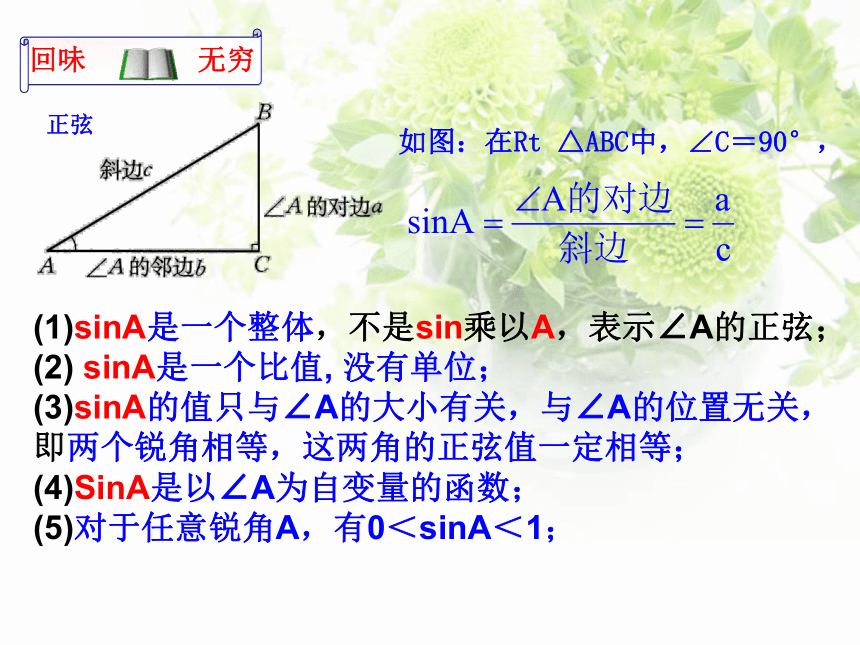
如图:在Rt △ABC中,∠C=90°,
正弦
(1)sinA是一个整体,不是sin乘以A,表示∠A的正弦;
(2) sinA是一个比值, 没有单位;
(3)sinA的值只与∠A的大小有关,与∠A的位置无关,
即两个锐角相等,这两角的正弦值一定相等;
(4)SinA是以∠A为自变量的函数;
(5)对于任意锐角A,有0<sinA<1;
回味 无穷
1、你能将“其他边之比”用比例的式子表示出来吗?这样的比有多少?
2、当锐角A确定时,∠A的相邻直角边(邻边)与斜边的比、∠A的对边与邻边的比也都随之确定吗?为什么?
类比正弦的研究过程;根据相似三角形的性质来说明。
探究
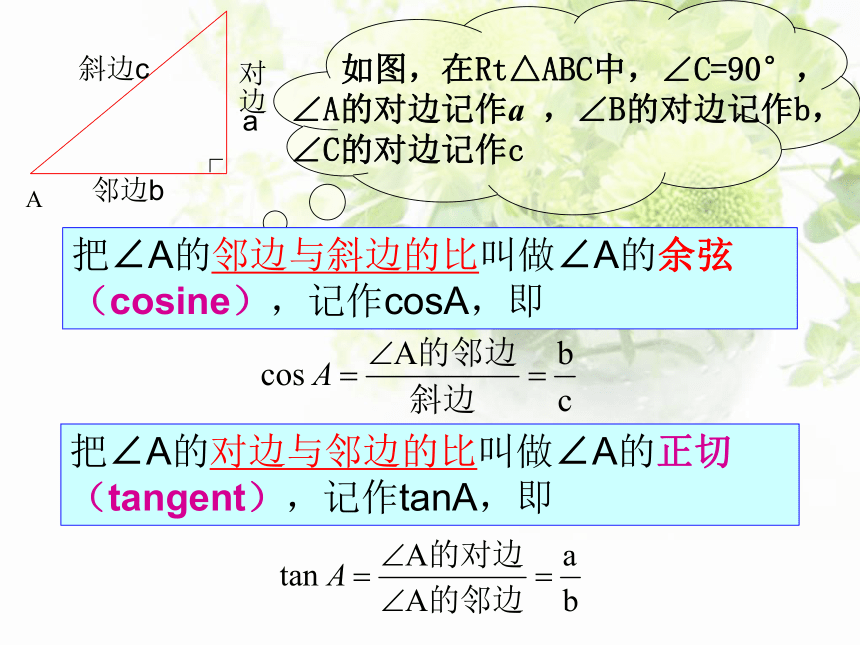
把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即
把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
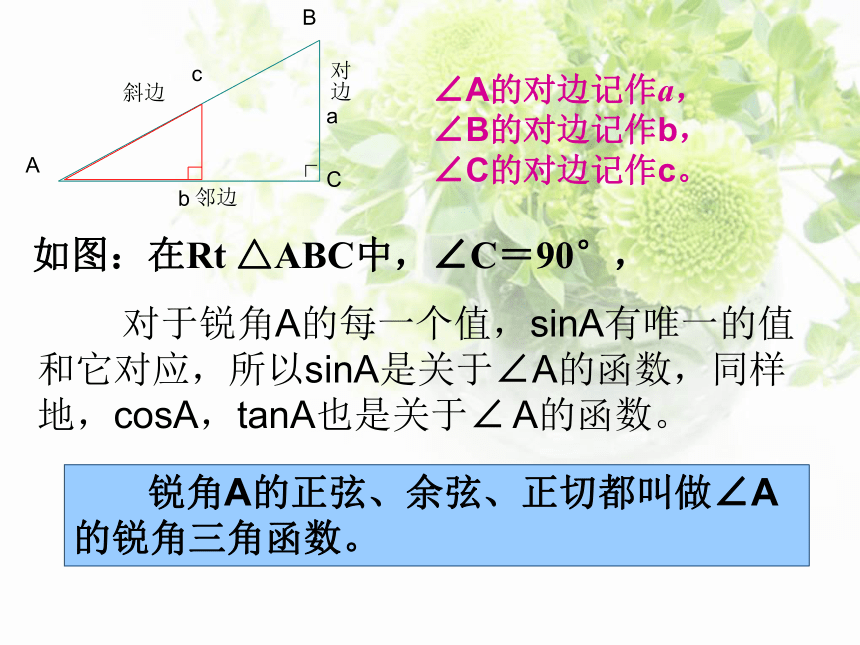
如图,在Rt△ABC中,∠C=90°,∠A的对边记作a ,∠B的对边记作b, ∠C的对边记作c
A
如图:在Rt △ABC中,∠C=90°,
∠A的对边记作a,
∠B的对边记作b,
∠C的对边记作c。
邻边
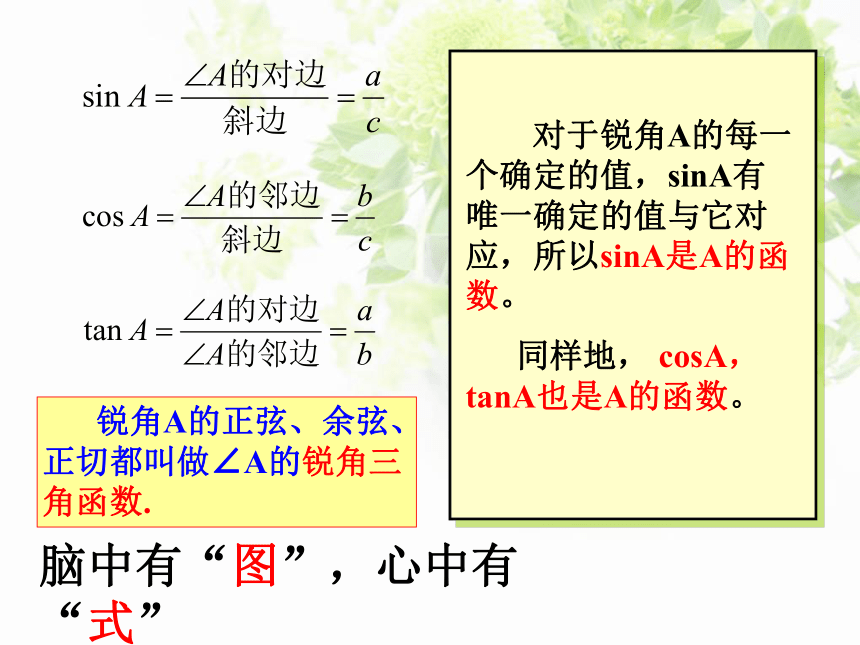
对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是关于∠A的函数,同样地,cosA,tanA也是关于∠ A的函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
脑中有“图”,心中有“式”
拓展:
1、已知,∠A是一个锐角,求∠A的各个三角函数的取值范围。
探究:锐角三角函数的性质.
2、增减性:根据锐角三角函数的定义探究
sinA随∠A的增大而增大;
cosA随∠A的增大而 ;
tanA随∠A的增大而 。
3、一个锐角的三角函数之间的关系
②求∠B的三角函数值.
延伸: 观察,对比上题的∠A,∠B的正弦、余弦、正切值,猜想一个直角三角形中的两个锐角的三角函数值有什么关系?
例1 如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.
延伸: 观察,对比上题的∠A,∠B的正弦、余弦、正切值,猜想一个直角三角形中的两个锐角的三角函数值有什么关系?
已知:在Rt △ABC中,∠C=90°,∠A+∠B=90°,
求证:
探究:互余的角的三角函数的关系.
证明:一个锐角的正弦等于它余角的余弦,这个锐角的余弦等于它余角的正弦,这个锐角的正切等于它余角正切的倒数.
①cos60°=sin ;
②tanA·tan50°=1,则A= ;
②tan37°≈0.75,则tan53°≈ .
巩固提高:
3、某市计划在一块三角形空地上种植草皮来美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮需要 元
5、如图,在△ABC中, AB=BC=5,sinA=0.8,
求sinB。
思考:用上面的方法我们还可以求出哪些角度的三角函数?
6.如图,为了测量河两岸A.B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于( )
A.a·sinα B.a·tanα
C.a·cosα D.
【解析】选B.在Rt△ABC中,tanα=
所以AB=a·tanα
如图,在四边形ABCD中, AB=2,CD=1,∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
A
B
C
D
E
2
1
60°
F
数学九年级下册
如图:在Rt △ABC中,∠C=90°,
正弦
(1)sinA是一个整体,不是sin乘以A,表示∠A的正弦;
(2) sinA是一个比值, 没有单位;
(3)sinA的值只与∠A的大小有关,与∠A的位置无关,
即两个锐角相等,这两角的正弦值一定相等;
(4)SinA是以∠A为自变量的函数;
(5)对于任意锐角A,有0<sinA<1;
回味 无穷
1、你能将“其他边之比”用比例的式子表示出来吗?这样的比有多少?
2、当锐角A确定时,∠A的相邻直角边(邻边)与斜边的比、∠A的对边与邻边的比也都随之确定吗?为什么?
类比正弦的研究过程;根据相似三角形的性质来说明。
探究
把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即
把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
如图,在Rt△ABC中,∠C=90°,∠A的对边记作a ,∠B的对边记作b, ∠C的对边记作c
A
如图:在Rt △ABC中,∠C=90°,
∠A的对边记作a,
∠B的对边记作b,
∠C的对边记作c。
邻边
对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是关于∠A的函数,同样地,cosA,tanA也是关于∠ A的函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
脑中有“图”,心中有“式”
拓展:
1、已知,∠A是一个锐角,求∠A的各个三角函数的取值范围。
探究:锐角三角函数的性质.
2、增减性:根据锐角三角函数的定义探究
sinA随∠A的增大而增大;
cosA随∠A的增大而 ;
tanA随∠A的增大而 。
3、一个锐角的三角函数之间的关系
②求∠B的三角函数值.
延伸: 观察,对比上题的∠A,∠B的正弦、余弦、正切值,猜想一个直角三角形中的两个锐角的三角函数值有什么关系?
例1 如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.
延伸: 观察,对比上题的∠A,∠B的正弦、余弦、正切值,猜想一个直角三角形中的两个锐角的三角函数值有什么关系?
已知:在Rt △ABC中,∠C=90°,∠A+∠B=90°,
求证:
探究:互余的角的三角函数的关系.
证明:一个锐角的正弦等于它余角的余弦,这个锐角的余弦等于它余角的正弦,这个锐角的正切等于它余角正切的倒数.
①cos60°=sin ;
②tanA·tan50°=1,则A= ;
②tan37°≈0.75,则tan53°≈ .
巩固提高:
3、某市计划在一块三角形空地上种植草皮来美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮需要 元
5、如图,在△ABC中, AB=BC=5,sinA=0.8,
求sinB。
思考:用上面的方法我们还可以求出哪些角度的三角函数?
6.如图,为了测量河两岸A.B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于( )
A.a·sinα B.a·tanα
C.a·cosα D.
【解析】选B.在Rt△ABC中,tanα=
所以AB=a·tanα
如图,在四边形ABCD中, AB=2,CD=1,∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
A
B
C
D
E
2
1
60°
F
