人教版高中物理选修3-3 学案第八章 气体 第2节气体的等容变化和等压变化 Word版含解析
文档属性
| 名称 | 人教版高中物理选修3-3 学案第八章 气体 第2节气体的等容变化和等压变化 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 262.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-02 10:15:12 | ||
图片预览




文档简介
第2节 气体的等容变化和等压变化
1.知道什么是等容变化和等压变化。
2.知道查理定律和盖—吕萨克定律的内容、表达式及适用条件,并会用气体变化规律解决实际问题。
3.理解p-T图象、V-T图象的物理意义。
一、气体的等容变化
1.等容变化:一定质量的气体在体积不变时,压强随温度的变化。
2.查理定律
(1)内容:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比。
(2)表达式:p=CT或=C或=或=。
(3)图象
(4)适用条件:①气体的质量不变;②气体的体积不变。
二、气体的等压变化
1.等压变化:一定质量的某种气体,在压强不变时,体积随温度的变化。
2.盖—吕萨克定律
(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(2)表达式:V=CT或=C或=或=。
(3)图象
(4)适用条件:①气体的质量不变;②气体的压强不变。
判一判
(1)对于一定质量的气体,在体积不变时,压强增大到原来的二倍,则气体的摄氏温度升高到原来的二倍。( )
(2)一定质量的气体,体积不变时,压强与摄氏温度成正比。( )
(3)V-t图象中,等压线是一条过原点的直线。( )
提示:(1)× (2)× (3)×
课堂任务 查理定律及其应用
1.查理定律的表述
(1)==C;
(2)=;
(3)=(p0为0 ℃时气体的压强),也可表述为:一定质量的气体,当体积不变时,温度每升高(或降低)1 ℃,增大(或减小)的压强等于它在0 ℃时压强的,即=或pt=p0。
2.对等容线的理解
(1)p-t图中的等容线
①p-t图中的等容线是一条延长线通过横坐标-273 ℃的倾斜直线。
②图甲中纵轴上的截距p0是气体0 ℃时的压强。
③等容线的斜率和气体的体积大小有关,体积越大,斜率越小。如图乙所示,一定质量的某种气体,四条等容线的体积关系为:V1>V2>V3>V4。
(2)p-T图中的等容线
①p-T图中等容线是一条延长线通过原点的倾斜直线。
②斜率k==C(常数)与气体体积有关,体积越大,斜率越小。如图丙所示,一定质量的某种气体,四条等容线的体积关系为:V1>V2>V3>V4。
例1 用易拉罐盛装碳酸饮料非常卫生和方便,但如果剧烈碰撞或严重受热会导致爆炸。我们通常用的可乐易拉罐容积V=355 mL。假设在室温(17 ℃)时,罐内装有0.9V的饮料,剩余空间充满CO2气体,气体压强为1 atm。若易拉罐承受的压强为1.2 atm,则保存温度不能超过多少?
[规范解答] 易拉罐中气体在温度升高时做等容变化,当罐内压强升高到1.2 atm,对应的温度就是最高保存温度。
取CO2气体为研究对象,则:
初态:p1=1 atm,T1=(273+17) K=290 K,
末态:p2=1.2 atm,T2=未知量,
气体发生等容变化,由查理定律=得:
T2=T1= K=348 K,
t=(348-273) ℃=75 ℃。
[完美答案] 75 ℃
1.应用查理定律时的注意事项
(1)给出的温度是摄氏温度,必须换算为热力学温度;
(2)计算中压强的单位只要统一即可,没必要用国际单位。
2.应用假设法分析液柱移动问题的基本思路
当气体的状态参量发生变化而使液柱可能发生移动时,先假设其中一个参量(一般设为体积)不变(即假设水银柱不移动(;以此为前提,再运用相关的气体定律(如查理定律(进行分析讨论,看讨论结果是否与假设相符。若相符,则原假设成立;若讨论结果与假设相矛盾,说明原假设不成立,从而也就推出了正确的结论。分析的关键在于合理选择研究对象,正确地进行受力分析,然后通过比较作出判断。
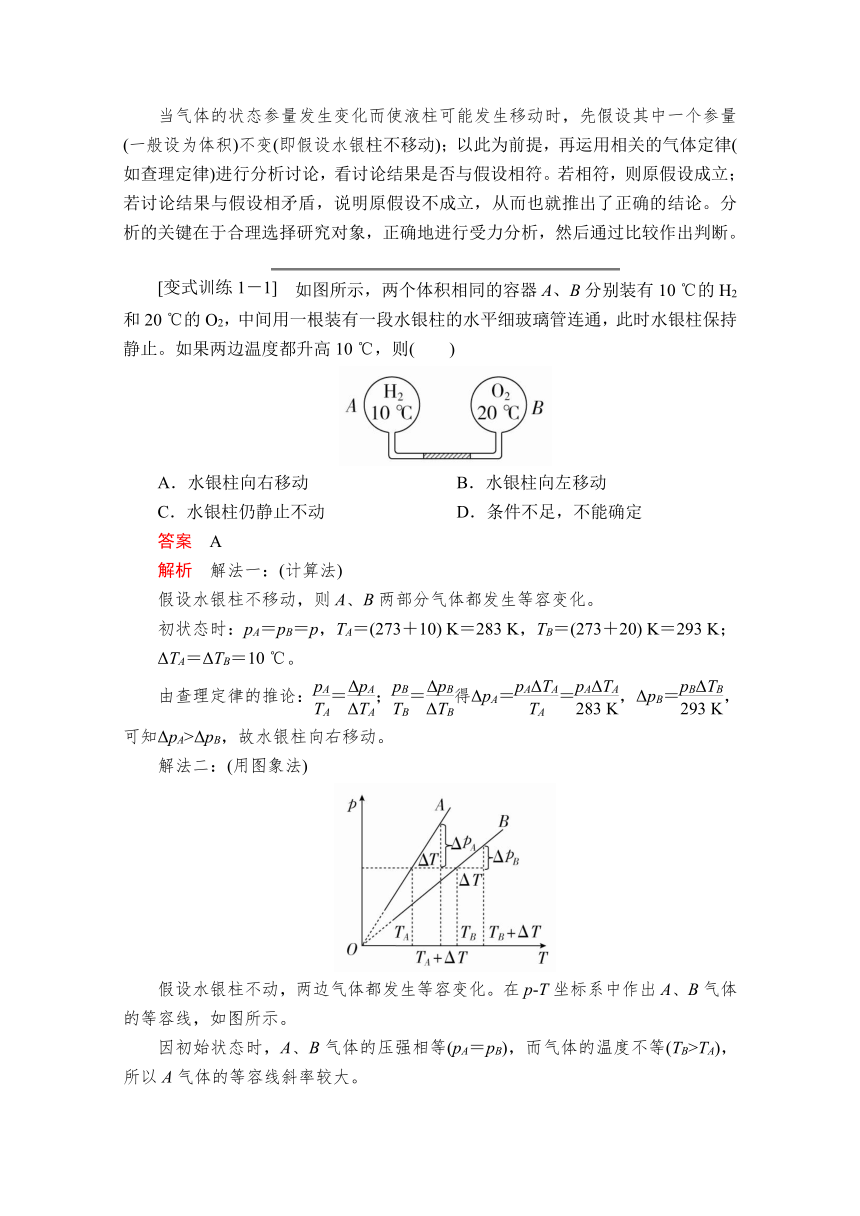
如图所示,两个体积相同的容器A、B分别装有10 ℃的H2和20 ℃的O2,中间用一根装有一段水银柱的水平细玻璃管连通,此时水银柱保持静止。如果两边温度都升高10 ℃,则( )
A.水银柱向右移动 B.水银柱向左移动
C.水银柱仍静止不动 D.条件不足,不能确定
答案 A
解析 解法一:(计算法)
假设水银柱不移动,则A、B两部分气体都发生等容变化。
初状态时:pA=pB=p,TA=(273+10) K=283 K,TB=(273+20) K=293 K;
ΔTA=ΔTB=10 ℃。
由查理定律的推论:=;=得ΔpA==,ΔpB=,可知ΔpA>ΔpB,故水银柱向右移动。
解法二:(用图象法)
假设水银柱不动,两边气体都发生等容变化。在p-T坐标系中作出A、B气体的等容线,如图所示。
因初始状态时,A、B气体的压强相等(pA=pB),而气体的温度不等(TB>TA),所以A气体的等容线斜率较大。
当温度增量相同时,从图象中很直观地看出,A内气体压强的增量ΔpA大于B内气体压强的增量ΔpB,故水银柱将向右移动。
如图所示,圆柱形汽缸倒置在水平粗糙地面上,汽缸内被活塞封闭有一定质量的空气。汽缸质量为M=10 kg,缸壁厚度不计,活塞质量m=5 kg,其面积S=50 cm2,与缸壁摩擦不计。在缸内气体温度为27 ℃时,活塞刚好与地面接触并对地面无压力。现设法使缸内气体温度升高,问当缸内气体温度升高到多少摄氏度时,汽缸对地面恰好无压力?(大气压强p0=105 Pa,g取10 m/s2)
答案 127 ℃
解析 当温度T1=(273+27) K=300 K时,活塞对地面恰好无压力,以活塞为研究对象,列平衡方程:
p1S+mg=p0S,
解得p1=p0-= Pa=0.9×105 Pa。
当气体温度升高,压强增大,汽缸恰好对地面无压力时,以汽缸为研究对象,列平衡方程:
p2S=p0S+Mg,
解得p2=p0+= Pa=1.2×105 Pa,
根据查理定律:=,得T2=T1=400 K,
解得:t=(400-273) ℃=127 ℃。
课堂任务 盖—吕萨克定律及其应用
1.盖—吕萨克定律的表述
(1)==C;
(2)=;
(3)=(V0为0 ℃时气体的体积),也可以表述为:一定质量的气体,当压强不变时,温度每升高(或降低)1 ℃,增大(或减小)的体积等于它在0 ℃时体积的,即=或Vt=V0。
2.对等压线的理解
(1)V-t图中的等压线
①V-t图中的等压线是一条延长线通过横坐标-273 ℃的倾斜直线。
②图甲中纵轴上的截距V0是气体0 ℃时的体积。
③等压线的斜率和气体的压强有关,压强越大,斜率越小。如图乙所示,一定质量的某种气体,四条等压线的压强关系为:p1>p2>p3>p4。
(2)V-T图中的等压线
①V-T图中的等压线是一条延长线通过原点的倾斜直线。
②斜率k==C(常数)与气体压强有关,压强越大,斜率越小。如图丙所示,一定质量的某种气体,四条等压线的压强关系为:p1>p2>p3>p4。
例2 如图所示,汽缸A中封闭有一定质量的气体,活塞B与A的接触是光滑且不漏气的,B上放一重物C,B与C的总重为G,大气压为p0。当汽缸内气体温度是20 ℃时,活塞与汽缸底部距离为h1;求当汽缸内气体温度是100 ℃时,活塞与汽缸底部的距离是多少?
[规范解答] 汽缸内气体温度发生变化时,汽缸内气体的压强保持不变,大小为p=p0+,其中S为活塞的横截面积。故此题用盖—吕萨克定律求解。
以汽缸内气体为研究对象。
初状态:热力学温度T1=(273+20) K=293 K,体积V1=h1S;
末状态:热力学温度T2=(273+100) K=373 K。
由盖—吕萨克定律=
求得V2=V1=h1S。
变化后活塞与汽缸底部的距离为
h2==h1=1.3h1。
[完美答案] 1.3h1
应用气体实验定律的解题思路
(1)确定研究对象,即研究哪部分气体。
(2)确定状态及状态参量,尤其注意压强的判断和计算。
(3)确定初末状态的温度、压强和体积,判断哪一状态参量不变,选择适当的气体实验定律。
(4)统一单位并列式求解。(其中温度只能用热力学温度单位——开尔文)
如图所示,上端开口的圆柱形汽缸竖直放置,截面积为0.2 m2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内。温度为300 K时,活塞离汽缸底部的高度为0.6 m;将气体加热到330 K时,活塞上升了0.05 m,不计摩擦力及固体体积的变化,求物体A的体积。
答案 0.02 m3
解析 对活塞受力分析如图所示,有pS=mg+p0S,由于活塞的受力情况不随温度的变化而变化,所以气体是等压变化。
设物体A的体积为V,则气体初末状态的参量分别为
初状态:V1=hS-V,T1=300 K,
末状态:V2=(h+Δh)S-V,T2=330 K
由盖—吕萨克定律=得=
代入数据解得V=0.02 m3。
1 mol的理想气体,其状态变化的p-V图线如图所示,请在p-T图、V-T图中画出对应的状态变化的图线。
答案 图见解析
解析 由于同一气体的状态变化可以用p-V图、V-T图、p-T图分别表示,因此p-V图、V-T图、p-T图之间可以相互转换。
1 mol的理想气体在标准状态下(1 atm,273 K)的体积是22.4 L,所以状态A的温度是273 K。
A到B的过程是等容变化,压强增大1倍,则温度升高1倍,所以B的温度是546 K。
B到C的过程是等压变化,体积增大1倍,则温度升高1倍,所以C的温度是1092 K。
C到D的过程是等容变化,压强减小倍,则温度降低一半,所以D的温度是546 K。
D到A的过程是等压变化,体积减小倍,则温度降低一半。因此,p-T图、V-T图分别如图甲、乙所示。
如图所示,是一定质量的气体从状态A经状态B、C到状态D的p-T图象,已知气体在状态B时的体积是8 L,求VA、VC和VD,并画出此过程的V-T图。
答案 VA=4 L VC=8 L VD=10.7 L V-T图见解析
解析 A→B,等温过程有pAVA=pBVB,所以
VA== L=4 L,
B→C,等容过程,所以VC=VB=8 L,
C→D,等压过程有=,VD=VC=×8 L=10.7 L。
此过程的V-T图如图所示。
1.知道什么是等容变化和等压变化。
2.知道查理定律和盖—吕萨克定律的内容、表达式及适用条件,并会用气体变化规律解决实际问题。
3.理解p-T图象、V-T图象的物理意义。
一、气体的等容变化
1.等容变化:一定质量的气体在体积不变时,压强随温度的变化。
2.查理定律
(1)内容:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比。
(2)表达式:p=CT或=C或=或=。
(3)图象
(4)适用条件:①气体的质量不变;②气体的体积不变。
二、气体的等压变化
1.等压变化:一定质量的某种气体,在压强不变时,体积随温度的变化。
2.盖—吕萨克定律
(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(2)表达式:V=CT或=C或=或=。
(3)图象
(4)适用条件:①气体的质量不变;②气体的压强不变。
判一判
(1)对于一定质量的气体,在体积不变时,压强增大到原来的二倍,则气体的摄氏温度升高到原来的二倍。( )
(2)一定质量的气体,体积不变时,压强与摄氏温度成正比。( )
(3)V-t图象中,等压线是一条过原点的直线。( )
提示:(1)× (2)× (3)×
课堂任务 查理定律及其应用
1.查理定律的表述
(1)==C;
(2)=;
(3)=(p0为0 ℃时气体的压强),也可表述为:一定质量的气体,当体积不变时,温度每升高(或降低)1 ℃,增大(或减小)的压强等于它在0 ℃时压强的,即=或pt=p0。
2.对等容线的理解
(1)p-t图中的等容线
①p-t图中的等容线是一条延长线通过横坐标-273 ℃的倾斜直线。
②图甲中纵轴上的截距p0是气体0 ℃时的压强。
③等容线的斜率和气体的体积大小有关,体积越大,斜率越小。如图乙所示,一定质量的某种气体,四条等容线的体积关系为:V1>V2>V3>V4。
(2)p-T图中的等容线
①p-T图中等容线是一条延长线通过原点的倾斜直线。
②斜率k==C(常数)与气体体积有关,体积越大,斜率越小。如图丙所示,一定质量的某种气体,四条等容线的体积关系为:V1>V2>V3>V4。
例1 用易拉罐盛装碳酸饮料非常卫生和方便,但如果剧烈碰撞或严重受热会导致爆炸。我们通常用的可乐易拉罐容积V=355 mL。假设在室温(17 ℃)时,罐内装有0.9V的饮料,剩余空间充满CO2气体,气体压强为1 atm。若易拉罐承受的压强为1.2 atm,则保存温度不能超过多少?
[规范解答] 易拉罐中气体在温度升高时做等容变化,当罐内压强升高到1.2 atm,对应的温度就是最高保存温度。
取CO2气体为研究对象,则:
初态:p1=1 atm,T1=(273+17) K=290 K,
末态:p2=1.2 atm,T2=未知量,
气体发生等容变化,由查理定律=得:
T2=T1= K=348 K,
t=(348-273) ℃=75 ℃。
[完美答案] 75 ℃
1.应用查理定律时的注意事项
(1)给出的温度是摄氏温度,必须换算为热力学温度;
(2)计算中压强的单位只要统一即可,没必要用国际单位。
2.应用假设法分析液柱移动问题的基本思路
当气体的状态参量发生变化而使液柱可能发生移动时,先假设其中一个参量(一般设为体积)不变(即假设水银柱不移动(;以此为前提,再运用相关的气体定律(如查理定律(进行分析讨论,看讨论结果是否与假设相符。若相符,则原假设成立;若讨论结果与假设相矛盾,说明原假设不成立,从而也就推出了正确的结论。分析的关键在于合理选择研究对象,正确地进行受力分析,然后通过比较作出判断。
如图所示,两个体积相同的容器A、B分别装有10 ℃的H2和20 ℃的O2,中间用一根装有一段水银柱的水平细玻璃管连通,此时水银柱保持静止。如果两边温度都升高10 ℃,则( )
A.水银柱向右移动 B.水银柱向左移动
C.水银柱仍静止不动 D.条件不足,不能确定
答案 A
解析 解法一:(计算法)
假设水银柱不移动,则A、B两部分气体都发生等容变化。
初状态时:pA=pB=p,TA=(273+10) K=283 K,TB=(273+20) K=293 K;
ΔTA=ΔTB=10 ℃。
由查理定律的推论:=;=得ΔpA==,ΔpB=,可知ΔpA>ΔpB,故水银柱向右移动。
解法二:(用图象法)
假设水银柱不动,两边气体都发生等容变化。在p-T坐标系中作出A、B气体的等容线,如图所示。
因初始状态时,A、B气体的压强相等(pA=pB),而气体的温度不等(TB>TA),所以A气体的等容线斜率较大。
当温度增量相同时,从图象中很直观地看出,A内气体压强的增量ΔpA大于B内气体压强的增量ΔpB,故水银柱将向右移动。
如图所示,圆柱形汽缸倒置在水平粗糙地面上,汽缸内被活塞封闭有一定质量的空气。汽缸质量为M=10 kg,缸壁厚度不计,活塞质量m=5 kg,其面积S=50 cm2,与缸壁摩擦不计。在缸内气体温度为27 ℃时,活塞刚好与地面接触并对地面无压力。现设法使缸内气体温度升高,问当缸内气体温度升高到多少摄氏度时,汽缸对地面恰好无压力?(大气压强p0=105 Pa,g取10 m/s2)
答案 127 ℃
解析 当温度T1=(273+27) K=300 K时,活塞对地面恰好无压力,以活塞为研究对象,列平衡方程:
p1S+mg=p0S,
解得p1=p0-= Pa=0.9×105 Pa。
当气体温度升高,压强增大,汽缸恰好对地面无压力时,以汽缸为研究对象,列平衡方程:
p2S=p0S+Mg,
解得p2=p0+= Pa=1.2×105 Pa,
根据查理定律:=,得T2=T1=400 K,
解得:t=(400-273) ℃=127 ℃。
课堂任务 盖—吕萨克定律及其应用
1.盖—吕萨克定律的表述
(1)==C;
(2)=;
(3)=(V0为0 ℃时气体的体积),也可以表述为:一定质量的气体,当压强不变时,温度每升高(或降低)1 ℃,增大(或减小)的体积等于它在0 ℃时体积的,即=或Vt=V0。
2.对等压线的理解
(1)V-t图中的等压线
①V-t图中的等压线是一条延长线通过横坐标-273 ℃的倾斜直线。
②图甲中纵轴上的截距V0是气体0 ℃时的体积。
③等压线的斜率和气体的压强有关,压强越大,斜率越小。如图乙所示,一定质量的某种气体,四条等压线的压强关系为:p1>p2>p3>p4。
(2)V-T图中的等压线
①V-T图中的等压线是一条延长线通过原点的倾斜直线。
②斜率k==C(常数)与气体压强有关,压强越大,斜率越小。如图丙所示,一定质量的某种气体,四条等压线的压强关系为:p1>p2>p3>p4。
例2 如图所示,汽缸A中封闭有一定质量的气体,活塞B与A的接触是光滑且不漏气的,B上放一重物C,B与C的总重为G,大气压为p0。当汽缸内气体温度是20 ℃时,活塞与汽缸底部距离为h1;求当汽缸内气体温度是100 ℃时,活塞与汽缸底部的距离是多少?
[规范解答] 汽缸内气体温度发生变化时,汽缸内气体的压强保持不变,大小为p=p0+,其中S为活塞的横截面积。故此题用盖—吕萨克定律求解。
以汽缸内气体为研究对象。
初状态:热力学温度T1=(273+20) K=293 K,体积V1=h1S;
末状态:热力学温度T2=(273+100) K=373 K。
由盖—吕萨克定律=
求得V2=V1=h1S。
变化后活塞与汽缸底部的距离为
h2==h1=1.3h1。
[完美答案] 1.3h1
应用气体实验定律的解题思路
(1)确定研究对象,即研究哪部分气体。
(2)确定状态及状态参量,尤其注意压强的判断和计算。
(3)确定初末状态的温度、压强和体积,判断哪一状态参量不变,选择适当的气体实验定律。
(4)统一单位并列式求解。(其中温度只能用热力学温度单位——开尔文)
如图所示,上端开口的圆柱形汽缸竖直放置,截面积为0.2 m2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内。温度为300 K时,活塞离汽缸底部的高度为0.6 m;将气体加热到330 K时,活塞上升了0.05 m,不计摩擦力及固体体积的变化,求物体A的体积。
答案 0.02 m3
解析 对活塞受力分析如图所示,有pS=mg+p0S,由于活塞的受力情况不随温度的变化而变化,所以气体是等压变化。
设物体A的体积为V,则气体初末状态的参量分别为
初状态:V1=hS-V,T1=300 K,
末状态:V2=(h+Δh)S-V,T2=330 K
由盖—吕萨克定律=得=
代入数据解得V=0.02 m3。
1 mol的理想气体,其状态变化的p-V图线如图所示,请在p-T图、V-T图中画出对应的状态变化的图线。
答案 图见解析
解析 由于同一气体的状态变化可以用p-V图、V-T图、p-T图分别表示,因此p-V图、V-T图、p-T图之间可以相互转换。
1 mol的理想气体在标准状态下(1 atm,273 K)的体积是22.4 L,所以状态A的温度是273 K。
A到B的过程是等容变化,压强增大1倍,则温度升高1倍,所以B的温度是546 K。
B到C的过程是等压变化,体积增大1倍,则温度升高1倍,所以C的温度是1092 K。
C到D的过程是等容变化,压强减小倍,则温度降低一半,所以D的温度是546 K。
D到A的过程是等压变化,体积减小倍,则温度降低一半。因此,p-T图、V-T图分别如图甲、乙所示。
如图所示,是一定质量的气体从状态A经状态B、C到状态D的p-T图象,已知气体在状态B时的体积是8 L,求VA、VC和VD,并画出此过程的V-T图。
答案 VA=4 L VC=8 L VD=10.7 L V-T图见解析
解析 A→B,等温过程有pAVA=pBVB,所以
VA== L=4 L,
B→C,等容过程,所以VC=VB=8 L,
C→D,等压过程有=,VD=VC=×8 L=10.7 L。
此过程的V-T图如图所示。
