北师大版数学七年级下册 第三单元 变量之间的关系综合测试卷(解析版)
文档属性
| 名称 | 北师大版数学七年级下册 第三单元 变量之间的关系综合测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 833.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 11:03:01 | ||
图片预览


文档简介
第三章 综合测试卷
一、选择题.
01 小刚以400米/分的速度匀速骑车5分钟,在原地休息了6分钟,然后以500米/分的速度骑回出发地.下列图象能表达这一过程的是 ( )
A. B. C. D.
02甲,乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图,则下列说法正确的是 ( )
A.乙先到达终点
B.乙比甲跑的路程多
C.乙用的时间短
D.甲的速度比乙的速度快
03 如果一盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x(支)表示圆珠笔的支数,那么y与x之间的关系式应该是 ( )
A.y=12x B.y=18x C.y=x D.y=x
04货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地,已知甲,乙两地相距180千米,货车的速度为60千米/时,小汽车的速度为90千米/时,则下图中能反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(时)之间关系的图象是 ( )
A. B. C. D.
05周日,小冬骑共享单车,爸爸骑摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的关系图象如图,根据图象分析,下列说法正确的是 ( )
A.4分钟时相遇,爸爸先到B地
B.20分钟时相遇,爸爸先到B地
C.4分钟时相遇,小冬先到B地
D 20分钟时相遇,小冬先到B地
06(2017.北京)小苏和小林在如图①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)之间的关系如图②所示.下列叙述正确的是 ( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15 s跑过的路程大于小林前15 s跑过的路程
D.小林在跑最后100 m的过程中,与小苏相遇2次
二、填空题
07放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分)的关系如图所示,则小明的骑车速度是_______千米/分.
08小明从家跑步到学校,接着马上原路步行回家,如图是小明离家的路程y(米)与时间t(分)的关系图象,则小明回家的速度是_______米/分.
09如图,圆柱的高是3 cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化
(1)在这个变化中,自变量是________,因变量是________;
(2)当底面半径由1 cm变化到10 cm时,圆柱的体积增加了________cm?(结果保留π).
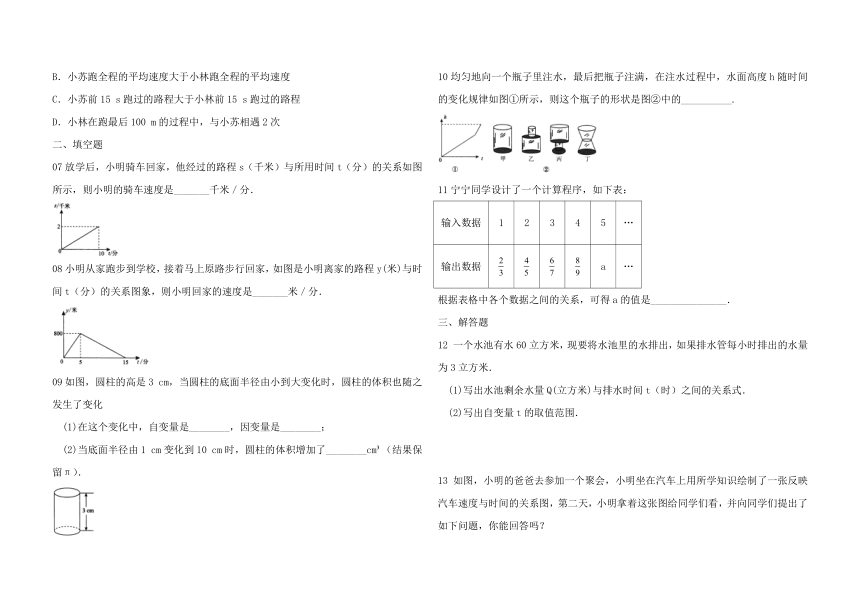
10均匀地向一个瓶子里注水,最后把瓶子注满,在注水过程中,水面高度h随时间的变化规律如图①所示,则这个瓶子的形状是图②中的__________.
11宁宁同学设计了一个计算程序,如下表:
输入数据 1 2 3 4 5 …
输出数据 a …
根据表格中各个数据之间的关系,可得a的值是_______________.
三、解答题
12 一个水池有水60立方米,现要将水池里的水排出,如果排水管每小时排出的水量为3立方米.
(1)写出水池剩余水量Q(立方米)与排水时间t(时)之间的关系式.
(2)写出自变量t的取值范围.
13 如图,小明的爸爸去参加一个聚会,小明坐在汽车上用所学知识绘制了一张反映汽车速度与时间的关系图,第二天,小明拿着这张图给同学们看,并向同学们提出了如下问题,你能回答吗?
(1)自变量是什么?因变量是什么?
(2)汽车共行驶了多长时间?最高时速是多少?
(3)汽车在哪段时间保持匀速?
14 某玉米种子的价格为每千克5元,如果一次购买2千克以上的种子,那么超过2千克部分的种子的价格打8折.
(1)根据题意,填写下表;
购买种子的数量/千克 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(2)设购买种子的数量为x千克,付款金额为y元,求y与x之间的关系式.
(3)若小张一次购买该种子花费了30元,求他购买种子的数量.
15 一个梯形的下底比上底长2厘米,它的高为3厘米.设它的上底长为x厘米,它的面积为y平方厘米.
(1)写出y与x之间的关系式,并指出哪个变量是自变量,哪个变量是因变量.
(2)当x由5变到7时,y如何变化?
(3)用表格表示当x从3变到10时(每次增加1),y的相应值.
(4)当x每增加1时,y如何变化?
(5)这个梯形的面积能等于9平方厘米吗?能等于2平方厘米吗?为什么?
16 如图是某港口从O时~16时水深的变化情况.
(1)什么时候港口内水最深,深度约为多少?
(2)什么时候港口内水最浅,深度约为多少?
(3)在什么时间范围内水深在增加?
(4)在什么时间范围内水深在减少?
(5)A,B两点分别表示什么?
(6)12时的水深是多少?
(7)用自己的语言叙述O时~16时港口水深的变化情况,
17 张华上午8h骑自行车外出办事,如图表示他离家的距离s(km)与所用时间t(h)之间的关系图象.根据这个图象回答下列问题:
(1)张华何时在休息?休息了多长时间?这时他离家多远?
(2)他何时到达目的地?在那里逗留了多长时间?目的地离他家多远?
(3)他何时开始返回?何时到家?他返回时的平均速度是多少?
18 为纪念爱国诗人屈原,某市举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分)之间的图象,请你根据图象回答下列问题.
(1)在1-8分钟时,哪支龙舟队处在领先地位?
(2)在这次龙舟比赛中哪支龙舟队先到达终点,先到多长时间?
(3)甲队在这次比赛中的平均速度是多少?
第三章综合测试卷
01 C解析:由题意,得以400米∠分的速度匀速骑车5分钟,路程随时间匀速增加;在原地休息了6分钟,路程不变;以500米/分的速度骑回出发地,路程逐渐减少.故选C.
02 D解析:结合图象可知,两人同时出发,甲比乙先到达终点,甲的速度比乙的速度快,故选D
03 D解析:一盒圆珠笔的售价除以一盒圆珠笔的支数等于每支圆珠笔的售价,∴可得y=x.故选D.
04 C解析:由题意,得出发前货车和小汽车都距离乙地180千米,出发两小时后小汽车到达乙地,离乙地的距离变为零,再经过两小时小汽车又返回甲地,离乙地的距离又为180千米,经过三小时,货车到达乙地,离乙地的距离变为零,故C符合题意.故选C.
05 B解析:观察图象可知,20分钟时,两人的路程均为4千米,且爸爸先到B地,∴小冬和爸爸20分钟时相遇,爸爸先到B地.故选B.
06 D解析:由图象可知,两人从起跑线同时出发,小林先到达终点,故A错误;根据图象可知,两人从起跑线同时出发,小林先到达终点,小苏后到达终点,小苏用的时间多,而路程相同,根据速度=,∴小苏牌全程的平均速度小于小林跑全程的平均速度,故B错误;根据图象可知,小苏前15 s跑过的路程小于小林前15 s跑过的路程,故C错误;小林在跑最后100 m的过程中,两人相遇时,即实线与虚线相交的地方,由图象可知有2次,故D正确.故选D.
07 0.2解析:由纵轴看出路程是2千米,由横轴看出时间是10分钟,∴小明的骑车速度是2÷10 =0.2(千米/分).故答案为0.2.
08 80解析:通过题图可知,小明家距学校800米,小明从学校步行回家的时间是15-5=10(分),∴小明回家的速度是800÷10=80(米/分).
89 (1)圆柱的底面半径 圆柱的体积 (2)297π
10乙
11 解析:由表格中各个数据的规律,得输出数据的分子是从2开始的偶数,分母是从3开始的奇数,当输入数据是n时,输出结果是,∴a的值是.
12解:(1)Q=60-3t.
(2)令Q=0,得60-3t=0.t=20.
∴自变量t的取值范围是a≤t≤20.
13解:(1)自变量是时间,因变量是速度.
(2)由横轴可知,小车共行驶了55分钟,最高时速是90千米/时.
(3)35分钟到55分钟保持匀速.
14解:(1)10 18
(2)根据题意,得
当O≤x≤2时,种子的价格为每千克5元,
∴y=5x.
当x>2时,其中有2千克的种子按每千克5元计算,超过2千克的部分按每千克4元计算,∴y=5×2+4(x-2)=4x+2.
所以当O≤x≤2时,y=5x;当x>2时,y=4x+2.
(3)∵30>10,
∴购买种子的数量超过2千克,
∴4x+2=30,解得x=7.
故他购买种子的数量是7千克.
15解:(1)y=3x+3,其中x是自变量,y是因变量.
(2)当x由5变到7时,y由18变到24.
(3)
x 3 4 5 6 7 8 9 10
y 12 15 18 21 24 27 30 33
(4)x每增加1时,y增加3.
(5)能等于9平方厘米,不能等于2平方厘米,理由:当y=9时,3x+3=9,得x=2,∴这个梯形的面积能等于9平方厘米;当y=2时.3x+3=2,得x=,不符合实际情况.
∴这个梯形的面积不能等于2平方厘米.
16解:(1)3时和15时港口内水最深,深度约为6米.
(2)10时港口内水最浅,深度约为2米.
(3)在O时~3时和10时~15时这两个时间段内水深在增加.
(4)在3时~10时和15时~16时这两个时间段内水深在减少.
(5)A点表示O时的水深为4米,B点表示8时的水深为3米.
(6)12时的水深为3米.
(7)略.
17解:(1)从图象中可以看出张华从9:00到9:30在休息;休息了半个小时;这时他离家15 km
(2)从图象中可以得到张华11:00到达目的地;在那里逗留了1个小时,目的地离家30 km.
(3)他12:OO开始返回;14:OO到家;返回时用了2个小时,行了30 km,返回时的平均速度为”(km/h).故张华返回时的平均速度为15 km/h.
18解:(1)由图象可知,t=1.8时,,
∴甲龙舟队处于领先地位.
(2)由图象可知,当t=4时,=1000,当t=3.8时,=1000,
∴乙龙舟队先到达终点,乙比甲先到0.2分钟.
(3)甲队在这次比赛中的平均速度是1000÷4=250(米/分).
一、选择题.
01 小刚以400米/分的速度匀速骑车5分钟,在原地休息了6分钟,然后以500米/分的速度骑回出发地.下列图象能表达这一过程的是 ( )
A. B. C. D.
02甲,乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图,则下列说法正确的是 ( )
A.乙先到达终点
B.乙比甲跑的路程多
C.乙用的时间短
D.甲的速度比乙的速度快
03 如果一盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x(支)表示圆珠笔的支数,那么y与x之间的关系式应该是 ( )
A.y=12x B.y=18x C.y=x D.y=x
04货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地,已知甲,乙两地相距180千米,货车的速度为60千米/时,小汽车的速度为90千米/时,则下图中能反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(时)之间关系的图象是 ( )
A. B. C. D.
05周日,小冬骑共享单车,爸爸骑摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的关系图象如图,根据图象分析,下列说法正确的是 ( )
A.4分钟时相遇,爸爸先到B地
B.20分钟时相遇,爸爸先到B地
C.4分钟时相遇,小冬先到B地
D 20分钟时相遇,小冬先到B地
06(2017.北京)小苏和小林在如图①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)之间的关系如图②所示.下列叙述正确的是 ( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15 s跑过的路程大于小林前15 s跑过的路程
D.小林在跑最后100 m的过程中,与小苏相遇2次
二、填空题
07放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分)的关系如图所示,则小明的骑车速度是_______千米/分.
08小明从家跑步到学校,接着马上原路步行回家,如图是小明离家的路程y(米)与时间t(分)的关系图象,则小明回家的速度是_______米/分.
09如图,圆柱的高是3 cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化
(1)在这个变化中,自变量是________,因变量是________;
(2)当底面半径由1 cm变化到10 cm时,圆柱的体积增加了________cm?(结果保留π).
10均匀地向一个瓶子里注水,最后把瓶子注满,在注水过程中,水面高度h随时间的变化规律如图①所示,则这个瓶子的形状是图②中的__________.
11宁宁同学设计了一个计算程序,如下表:
输入数据 1 2 3 4 5 …
输出数据 a …
根据表格中各个数据之间的关系,可得a的值是_______________.
三、解答题
12 一个水池有水60立方米,现要将水池里的水排出,如果排水管每小时排出的水量为3立方米.
(1)写出水池剩余水量Q(立方米)与排水时间t(时)之间的关系式.
(2)写出自变量t的取值范围.
13 如图,小明的爸爸去参加一个聚会,小明坐在汽车上用所学知识绘制了一张反映汽车速度与时间的关系图,第二天,小明拿着这张图给同学们看,并向同学们提出了如下问题,你能回答吗?
(1)自变量是什么?因变量是什么?
(2)汽车共行驶了多长时间?最高时速是多少?
(3)汽车在哪段时间保持匀速?
14 某玉米种子的价格为每千克5元,如果一次购买2千克以上的种子,那么超过2千克部分的种子的价格打8折.
(1)根据题意,填写下表;
购买种子的数量/千克 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(2)设购买种子的数量为x千克,付款金额为y元,求y与x之间的关系式.
(3)若小张一次购买该种子花费了30元,求他购买种子的数量.
15 一个梯形的下底比上底长2厘米,它的高为3厘米.设它的上底长为x厘米,它的面积为y平方厘米.
(1)写出y与x之间的关系式,并指出哪个变量是自变量,哪个变量是因变量.
(2)当x由5变到7时,y如何变化?
(3)用表格表示当x从3变到10时(每次增加1),y的相应值.
(4)当x每增加1时,y如何变化?
(5)这个梯形的面积能等于9平方厘米吗?能等于2平方厘米吗?为什么?
16 如图是某港口从O时~16时水深的变化情况.
(1)什么时候港口内水最深,深度约为多少?
(2)什么时候港口内水最浅,深度约为多少?
(3)在什么时间范围内水深在增加?
(4)在什么时间范围内水深在减少?
(5)A,B两点分别表示什么?
(6)12时的水深是多少?
(7)用自己的语言叙述O时~16时港口水深的变化情况,
17 张华上午8h骑自行车外出办事,如图表示他离家的距离s(km)与所用时间t(h)之间的关系图象.根据这个图象回答下列问题:
(1)张华何时在休息?休息了多长时间?这时他离家多远?
(2)他何时到达目的地?在那里逗留了多长时间?目的地离他家多远?
(3)他何时开始返回?何时到家?他返回时的平均速度是多少?
18 为纪念爱国诗人屈原,某市举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分)之间的图象,请你根据图象回答下列问题.
(1)在1-8分钟时,哪支龙舟队处在领先地位?
(2)在这次龙舟比赛中哪支龙舟队先到达终点,先到多长时间?
(3)甲队在这次比赛中的平均速度是多少?
第三章综合测试卷
01 C解析:由题意,得以400米∠分的速度匀速骑车5分钟,路程随时间匀速增加;在原地休息了6分钟,路程不变;以500米/分的速度骑回出发地,路程逐渐减少.故选C.
02 D解析:结合图象可知,两人同时出发,甲比乙先到达终点,甲的速度比乙的速度快,故选D
03 D解析:一盒圆珠笔的售价除以一盒圆珠笔的支数等于每支圆珠笔的售价,∴可得y=x.故选D.
04 C解析:由题意,得出发前货车和小汽车都距离乙地180千米,出发两小时后小汽车到达乙地,离乙地的距离变为零,再经过两小时小汽车又返回甲地,离乙地的距离又为180千米,经过三小时,货车到达乙地,离乙地的距离变为零,故C符合题意.故选C.
05 B解析:观察图象可知,20分钟时,两人的路程均为4千米,且爸爸先到B地,∴小冬和爸爸20分钟时相遇,爸爸先到B地.故选B.
06 D解析:由图象可知,两人从起跑线同时出发,小林先到达终点,故A错误;根据图象可知,两人从起跑线同时出发,小林先到达终点,小苏后到达终点,小苏用的时间多,而路程相同,根据速度=,∴小苏牌全程的平均速度小于小林跑全程的平均速度,故B错误;根据图象可知,小苏前15 s跑过的路程小于小林前15 s跑过的路程,故C错误;小林在跑最后100 m的过程中,两人相遇时,即实线与虚线相交的地方,由图象可知有2次,故D正确.故选D.
07 0.2解析:由纵轴看出路程是2千米,由横轴看出时间是10分钟,∴小明的骑车速度是2÷10 =0.2(千米/分).故答案为0.2.
08 80解析:通过题图可知,小明家距学校800米,小明从学校步行回家的时间是15-5=10(分),∴小明回家的速度是800÷10=80(米/分).
89 (1)圆柱的底面半径 圆柱的体积 (2)297π
10乙
11 解析:由表格中各个数据的规律,得输出数据的分子是从2开始的偶数,分母是从3开始的奇数,当输入数据是n时,输出结果是,∴a的值是.
12解:(1)Q=60-3t.
(2)令Q=0,得60-3t=0.t=20.
∴自变量t的取值范围是a≤t≤20.
13解:(1)自变量是时间,因变量是速度.
(2)由横轴可知,小车共行驶了55分钟,最高时速是90千米/时.
(3)35分钟到55分钟保持匀速.
14解:(1)10 18
(2)根据题意,得
当O≤x≤2时,种子的价格为每千克5元,
∴y=5x.
当x>2时,其中有2千克的种子按每千克5元计算,超过2千克的部分按每千克4元计算,∴y=5×2+4(x-2)=4x+2.
所以当O≤x≤2时,y=5x;当x>2时,y=4x+2.
(3)∵30>10,
∴购买种子的数量超过2千克,
∴4x+2=30,解得x=7.
故他购买种子的数量是7千克.
15解:(1)y=3x+3,其中x是自变量,y是因变量.
(2)当x由5变到7时,y由18变到24.
(3)
x 3 4 5 6 7 8 9 10
y 12 15 18 21 24 27 30 33
(4)x每增加1时,y增加3.
(5)能等于9平方厘米,不能等于2平方厘米,理由:当y=9时,3x+3=9,得x=2,∴这个梯形的面积能等于9平方厘米;当y=2时.3x+3=2,得x=,不符合实际情况.
∴这个梯形的面积不能等于2平方厘米.
16解:(1)3时和15时港口内水最深,深度约为6米.
(2)10时港口内水最浅,深度约为2米.
(3)在O时~3时和10时~15时这两个时间段内水深在增加.
(4)在3时~10时和15时~16时这两个时间段内水深在减少.
(5)A点表示O时的水深为4米,B点表示8时的水深为3米.
(6)12时的水深为3米.
(7)略.
17解:(1)从图象中可以看出张华从9:00到9:30在休息;休息了半个小时;这时他离家15 km
(2)从图象中可以得到张华11:00到达目的地;在那里逗留了1个小时,目的地离家30 km.
(3)他12:OO开始返回;14:OO到家;返回时用了2个小时,行了30 km,返回时的平均速度为”(km/h).故张华返回时的平均速度为15 km/h.
18解:(1)由图象可知,t=1.8时,,
∴甲龙舟队处于领先地位.
(2)由图象可知,当t=4时,=1000,当t=3.8时,=1000,
∴乙龙舟队先到达终点,乙比甲先到0.2分钟.
(3)甲队在这次比赛中的平均速度是1000÷4=250(米/分).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
