2020年北师大版七年级上册数学《第1章 丰富的图形世界》单元测试卷(解析版)
文档属性
| 名称 | 2020年北师大版七年级上册数学《第1章 丰富的图形世界》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 431.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 14:03:30 | ||
图片预览

文档简介
2020年北师大版七年级上册数学《第1章 丰富的图形世界》单元测试卷
一.选择题(共10小题)
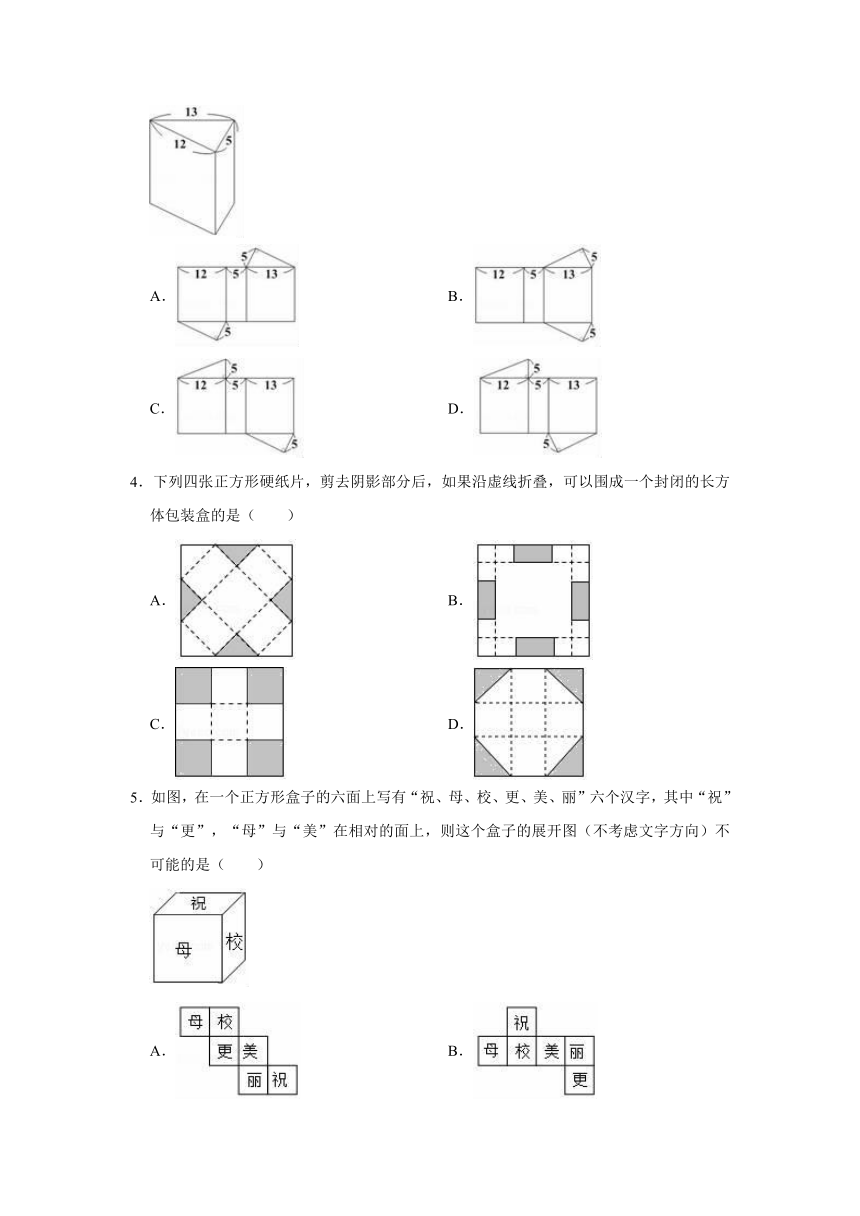
1.一个长方形的长和宽分别为3cm和2cm,依次以这个长方形的长和宽所在的直线为旋转轴,把长方形旋转1周形成圆柱体甲和圆柱体乙,两个圆柱体的体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙 B.V甲>V乙,S甲=S乙
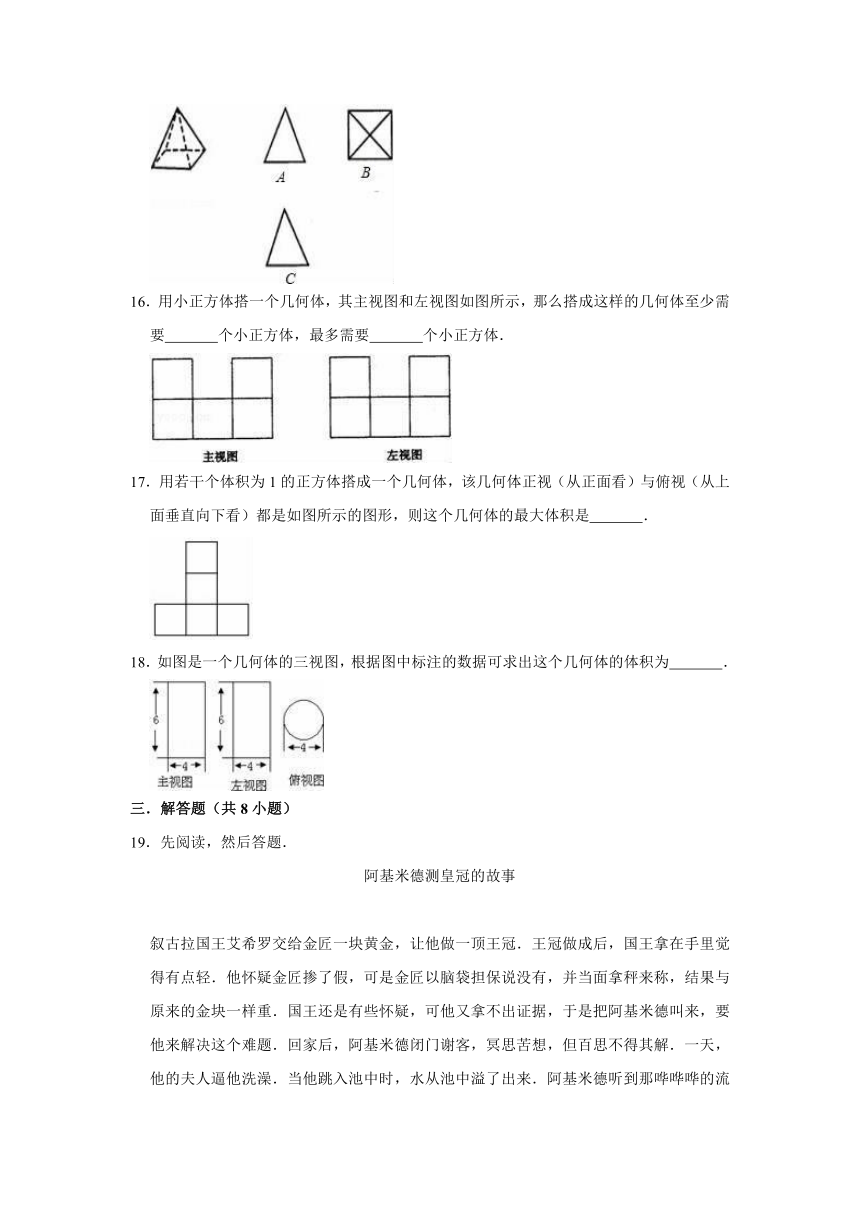
C.V甲=V乙,S甲=S乙 D.V甲>V乙,S甲<S乙
2.下列4个平面图形中,哪一个是由图中正方体纸盒展开得到的( )
A. B.
C. D.
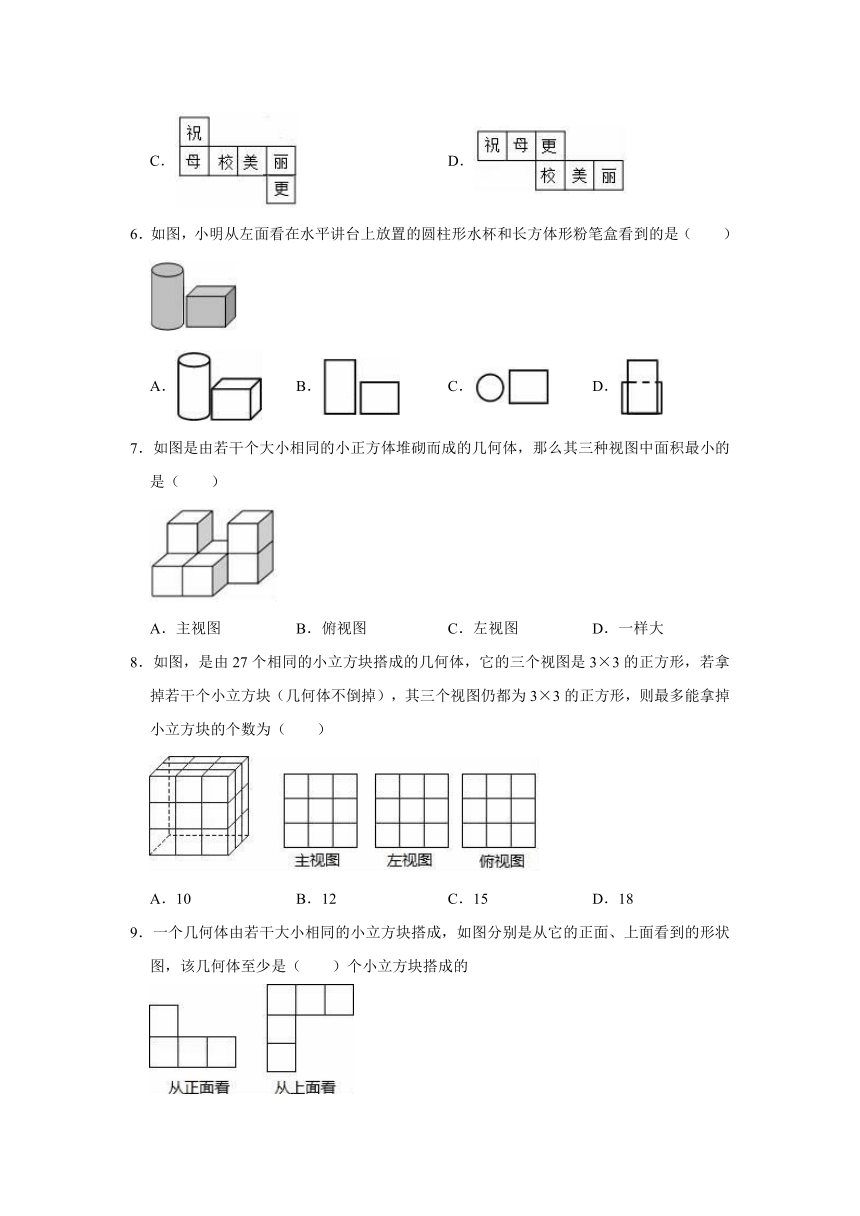
3.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A. B.
C. D.
4.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
C. D.
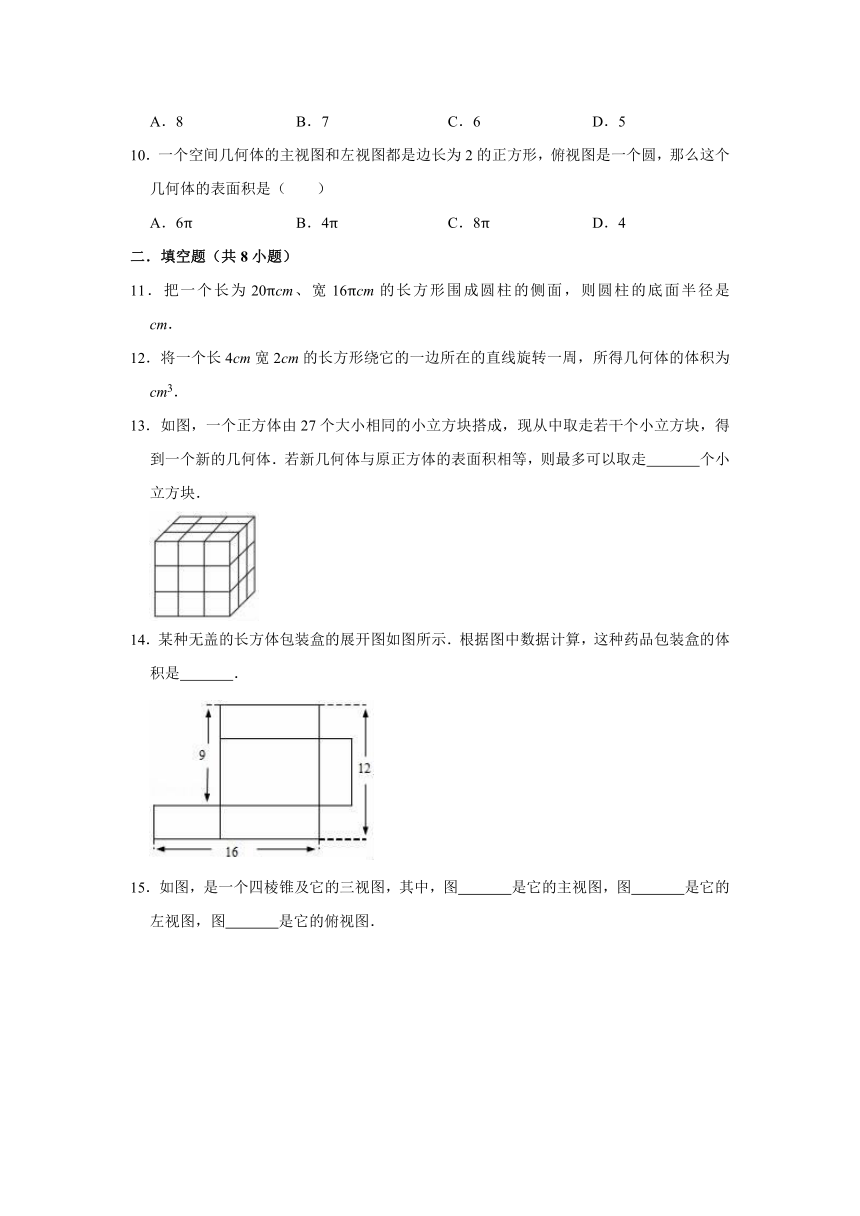
5.如图,在一个正方形盒子的六面上写有“祝、母、校、更、美、丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向)不可能的是( )
A. B.
C. D.
6.如图,小明从左面看在水平讲台上放置的圆柱形水杯和长方体形粉笔盒看到的是( )
A. B. C. D.
7.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
8.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )
A.10 B.12 C.15 D.18
9.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是( )个小立方块搭成的
A.8 B.7 C.6 D.5
10.一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积是( )
A.6π B.4π C.8π D.4
二.填空题(共8小题)
11.把一个长为20πcm、宽16πcm的长方形围成圆柱的侧面,则圆柱的底面半径是 cm.
12.将一个长4cm宽2cm的长方形绕它的一边所在的直线旋转一周,所得几何体的体积为 cm3.
13.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走 个小立方块.
14.某种无盖的长方体包装盒的展开图如图所示.根据图中数据计算,这种药品包装盒的体积是 .
15.如图,是一个四棱锥及它的三视图,其中,图 是它的主视图,图 是它的左视图,图 是它的俯视图.
16.用小正方体搭一个几何体,其主视图和左视图如图所示,那么搭成这样的几何体至少需要 个小正方体,最多需要 个小正方体.
17.用若干个体积为1的正方体搭成一个几何体,该几何体正视(从正面看)与俯视(从上面垂直向下看)都是如图所示的图形,则这个几何体的最大体积是 .
18.如图是一个几何体的三视图,根据图中标注的数据可求出这个几何体的体积为 .
三.解答题(共8小题)
19.先阅读,然后答题.
阿基米德测皇冠的故事
叙古拉国王艾希罗交给金匠一块黄金,让他做一顶王冠.王冠做成后,国王拿在手里觉得有点轻.他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿秤来称,结果与原来的金块一样重.国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题.回家后,阿基米德闭门谢客,冥思苦想,但百思不得其解.一天,他的夫人逼他洗澡.当他跳入池中时,水从池中溢了出来.阿基米德听到那哗哗哗的流水声,灵感一下子冒了出来.他从池中跳出来,连衣服都没穿,就冲到街上,高喊着:“优勒加!优勒加!(意为发现了)“.夫人这回可真着急了,嘴里嘟囔着“真疯了,真疯了“,便随后追了出去.街上的人不知发生了什么事,也都跟在后面追着看.原来,阿基米德由澡盆溢水找到了解决王冠问题的办法:相同质量的相同物质泡在水里,溢出的水的体积应该相同.如果把王冠放到水了,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假.阿基为德跑到王宫后立即找来一盆水,又找来同样重量的一块黄金,一块白银,分两次泡进盆里,白银溢出的水比黄金溢出的几乎要多一倍,然后他又把王冠和金块分别泡进水盆里,王冠溢出的水比金块多,显然王冠的质量不等于金块的质量,王冠里肯定掺了假.在铁的事实面前,金匠不得不低头承认,王冠里确实掺了白银.烦人的王冠之谜终于解开了.
小明受阿基米德测皇冠的故事的启发,想要做以下的一个探究:
小明准备了一个长方体的无盖容器和A,B两种型号的钢球若干.先往容器里加入一定量的水,如图,水高度为30mm,水足以淹没所有的钢球.
探究一:小明做了两次实验,先放入3个A型号钢球,水面的高度涨到36mm;把3个A型号钢球捞出,再放入2个B型号钢球,水面的高度恰好也涨到36mm.
由此可知A型号与B型号钢球的体积比为 ;
探究二:小明把之前的钢球全部捞出,然后再放入A型号与B型号钢球共10个后,水面高度涨到57mm,问放入水中的A型号与B型号钢球各几个?
20.由如图所示的图形绕虚线旋转一周得到的几何体有多少个面?其中多少个是平面?多少个是曲面?
21.一个长方体长、宽、高分别为4厘米、2厘米和1厘米.
(1)小明用斜二测画法画这个长方体的直观图时,长画4厘米,宽画 厘米,高画1厘米;
(2)如果用一根细铁丝做成这个长方体架子,不计材料损耗,至少需要多少厘米的铁丝?
(3)如果用8个这样相同的小长方体拼成一个正方体,那么此正方体的表面积是多少平方厘米?
22.如图是一个长方体的表面展开图,每个面都标注了字母,现在要把它折成长方体,并使F在前面,D面在右面,那么哪一个面会在上面?
23.如图是一颗骰子的三种不同的放置方法.
(1)根据图中三种放置方法,推出“?”处的点数.
(2)求这三个骰子下底面上点数和.
24.由7个相同的小立方块搭成的几何体如图所示,
(1)请画出它的三视图?
(2)请计算它的表面积?(棱长为1)
25.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
26.已知一个几何体的三视图如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1cm2)
2020年北师大版七年级上册数学《第1章 丰富的图形世界》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.一个长方形的长和宽分别为3cm和2cm,依次以这个长方形的长和宽所在的直线为旋转轴,把长方形旋转1周形成圆柱体甲和圆柱体乙,两个圆柱体的体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙 B.V甲>V乙,S甲=S乙
C.V甲=V乙,S甲=S乙 D.V甲>V乙,S甲<S乙
【分析】根据圆柱体的体积=底面积×高求解,再利用圆柱体侧面积求法得出答案.
【解答】解:由题可得,
V甲=π?22×3=12π,
V乙=π?32×2=18π,
∵12π<18π,
∴V甲<V乙;
∵S甲=2π×2×3=12π,
S乙=2π×3×2=12π,
∴S甲=S乙,
故选:A.
【点评】此题主要考查了面动成体,关键是掌握圆柱体的体积和侧面积计算公式.
2.下列4个平面图形中,哪一个是由图中正方体纸盒展开得到的( )
A. B.
C. D.
【分析】在验证立方体的展开图时,要细心观察每一个标志的位置是否一致,然后进行判断.
【解答】解:把四个选项的展开图折叠,能复原的是C.
故选:C.
【点评】本题考查正方体的表面展开图及空间想象能力.易错易混点:学生对相关图的位置想象不准确,从而错选,解决这类问题时,不妨动手实际操作一下,即可解决问题.
3.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A. B.
C. D.
【分析】三棱柱的侧面展开图是长方形,底面是三角形,据此进行判断即可.
【解答】解:A选项中,展开图下方的直角三角形的斜边长为12,不合题意;
B选项中,展开图上下两个直角三角形中的直角边不能与其它棱完全重合,不合题意;
C选项中,展开图下方的直角三角形中的直角边不能与其它棱完全重合,不合题意;
D选项中,展开图能折叠成一个三棱柱,符合题意;
故选:D.
【点评】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
4.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
C. D.
【分析】根据长方体的组成,通过结合立体图形与平面图形的相互转化,分别分析得出即可.
【解答】解:A、剪去阴影部分后,能组成长方体,故此选项正确;
B、剪去阴影部分后,无法组成长方体,故此选项不合题意;
C、剪去阴影部分后,组成无盖的正方体,故此选项不合题意;
D、剪去阴影部分后,无法组成长方体,故此选项不合题意;
故选:A.
【点评】此题主要考查了展开图折叠成几何体,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
5.如图,在一个正方形盒子的六面上写有“祝、母、校、更、美、丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向)不可能的是( )
A. B.
C. D.
【分析】根据立方体的平面展开图规律解决问题即可.
【解答】解:由图可得,“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图可能是A,B,C选项,
而D选项中,“更”与“祝”的位置有误,互换后则符合题意.
故选:D.
【点评】本题主要考查了正方体的展开图,对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
6.如图,小明从左面看在水平讲台上放置的圆柱形水杯和长方体形粉笔盒看到的是( )
A. B. C. D.
【分析】先细心观察原立体图形中圆柱和长方体的位置关系,找到从左面看所得到的图形即可.
【解答】解:圆柱的左视图是长方形,长方体的左视图是长方形,所以它们的左视图是:
故选:D.
【点评】考查简单组合体的三视图,解题时注意:左视图是从物体的左面看得到的视图.要注意几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线化成虚线.
7.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【解答】解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故选:C.
【点评】本题考查的是三视图的知识以及学生对该知识点的巩固.解题关键是找到三种视图的正方形的个数.
8.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )
A.10 B.12 C.15 D.18
【分析】拿掉若干个小立方块后保证几何体不倒掉,且三个视图仍都为3×3的正方形,所以最底下一层必须有9个小立方块,这样能保证俯视图仍为3×3的正方形,为保证正视图与左视图也为3×3的正方形,所以上面两层必须保留底面上一条对角线方向的三个立方块,即可得到最多能拿掉小立方块的个数.
【解答】解:根据题意,拿掉若干个小立方块后,三个视图仍都为3×3的正方形,
则最多能拿掉小立方块的个数为6+6=12个.
故选:B.
【点评】本题考查了几何体的三种视图,解决此类图的关键是由立体图形得到三视图.
9.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是( )个小立方块搭成的
A.8 B.7 C.6 D.5
【分析】根据题意可以得到该几何体从正面和上面看至少有多少个小立方体,综合考虑即可解答本题.
【解答】解:根据主视图可得,俯视图中第一列中至少一处有2层;
所以该几何体至少是用6个小立方块搭成的.
故选:C.
【点评】本题考查了由三视图判断几何体,由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
10.一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积是( )
A.6π B.4π C.8π D.4
【分析】根据题意,可判断出该几何体为圆柱.且已知底面半径以及高,易求表面积.
【解答】解:根据题目的描述,可以判断出这个几何体应该是个圆柱,且它的底面圆的半径为1,高为2,
那么它的表面积=2π×2+π×1×1×2=6π,故选:A.
【点评】本题要判断出几何体的形状然后再根据其面积公式进行计算,注意本题中的圆柱有上下底,不要漏掉任何一个.
二.填空题(共8小题)
11.把一个长为20πcm、宽16πcm的长方形围成圆柱的侧面,则圆柱的底面半径是 10或8 cm.
【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,或者长方形的宽等于底面周长,长等于圆柱的高,从而可以求出底面积半径.
【解答】解:分两种情况:
①20π÷(2×π)=10(cm),
故底面圆的半径为10cm,
②16π÷(2×π)=8(cm),
故底面圆的半径为8cm,
故答案为:10或8.
【点评】本题主要考查了立体图形,解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高.
12.将一个长4cm宽2cm的长方形绕它的一边所在的直线旋转一周,所得几何体的体积为 16π或32π cm3.
【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
【解答】解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).
故它们的体积分别为16πcm3或32πcm3.
故答案为:16π或32π.
【点评】本题考查圆柱体的体积的求法,注意分情况讨论.从运动的观点来看,点动成线,线动成面,面动成体.
13.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走 16 个小立方块.
【分析】根据表面积不变,只需留11个,分别是正中心的3个和四角上各2个.
【解答】解:若新几何体与原正方体的表面积相等,最多可以取走16个小正方体,只需留11个,分别是正中心的3个和四角上各2个,如图所示:
故答案为:16
【点评】本题主要考查了几何体的表面积.
14.某种无盖的长方体包装盒的展开图如图所示.根据图中数据计算,这种药品包装盒的体积是 180 .
【分析】先求出无盖长方体盒子的长、宽、高,再根据长方体的容积公式求出盒子的体积.
【解答】解:观察图形可知长方体盒子的高=12﹣9=3,宽=12﹣3×2=6,长=16﹣6=10,
则盒子的体积=3×10×6=180.
故答案为:180.
【点评】本题考查了几何体的展开图,正确理解无盖长方体的展开图,与原来长方体的之间的关系是解决本题的关键,长方体的容积=长×宽×高.
15.如图,是一个四棱锥及它的三视图,其中,图 C 是它的主视图,图 A 是它的左视图,图 B 是它的俯视图.
【分析】从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,根据三视图的概念判断即可.
【解答】解:从上面看四棱锥是一长方形加两条对角线,那么B是俯视图;由俯视图易得从正面看四棱锥是一个底边较大的三角形,故选C;从左面看四棱锥是一个底边较小的三角形,故选A.
【点评】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意所有看到的棱与顶点在三视图中都得表现出来.
16.用小正方体搭一个几何体,其主视图和左视图如图所示,那么搭成这样的几何体至少需要 5 个小正方体,最多需要 13 个小正方体.
【分析】根据图形,主视图的底层最多有9个小正方体,最少有3个小正方形.第二层最多有4个小正方形,最少有2个小正方形.
【解答】解:综合主视图和左视图,这个几何体的底层最多有3×3=9个小正方体,最少有3个小正方体,第二层最多有4个小正方体,最少有2个小正方体,那么搭成这样的几何体至少需要3+2=5个小正方体,最多需要4+9=13个小正方体.故答案为5个,13个.
【点评】本题要分别对最多和最少两种情况进行讨论,然后根据“俯视图打地基,正视图疯狂盖,左视图拆违章”来分析出小正方体的个数.
17.用若干个体积为1的正方体搭成一个几何体,该几何体正视(从正面看)与俯视(从上面垂直向下看)都是如图所示的图形,则这个几何体的最大体积是 11 .
【分析】由正视图、侧视图可知,体积最大时,俯视图中中间一列各个位置都有3个,两侧各1个,据此可得这个几何体的最大体积.
【解答】解:由正视图、侧视图可知,体积最大时,俯视图中中间一列各个位置都有3个,两侧各1个,共11个,
故这个几何体的最大体积是11.
故答案为:11.
【点评】本题主要考查了由三视图判断几何体,由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
18.如图是一个几何体的三视图,根据图中标注的数据可求出这个几何体的体积为 24π .
【分析】易得此几何体为圆柱,圆柱的体积=底面积×高,把相关数值代入即可求解.
【解答】解:此几何体为圆柱,体积为π×22×6=24π.
【点评】解决本题的关键是得到此几何体的形状,易错点是得到计算此几何体所需要的相关数据.
三.解答题(共8小题)
19.先阅读,然后答题.
阿基米德测皇冠的故事
叙古拉国王艾希罗交给金匠一块黄金,让他做一顶王冠.王冠做成后,国王拿在手里觉得有点轻.他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿秤来称,结果与原来的金块一样重.国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题.回家后,阿基米德闭门谢客,冥思苦想,但百思不得其解.一天,他的夫人逼他洗澡.当他跳入池中时,水从池中溢了出来.阿基米德听到那哗哗哗的流水声,灵感一下子冒了出来.他从池中跳出来,连衣服都没穿,就冲到街上,高喊着:“优勒加!优勒加!(意为发现了)“.夫人这回可真着急了,嘴里嘟囔着“真疯了,真疯了“,便随后追了出去.街上的人不知发生了什么事,也都跟在后面追着看.原来,阿基米德由澡盆溢水找到了解决王冠问题的办法:相同质量的相同物质泡在水里,溢出的水的体积应该相同.如果把王冠放到水了,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假.阿基为德跑到王宫后立即找来一盆水,又找来同样重量的一块黄金,一块白银,分两次泡进盆里,白银溢出的水比黄金溢出的几乎要多一倍,然后他又把王冠和金块分别泡进水盆里,王冠溢出的水比金块多,显然王冠的质量不等于金块的质量,王冠里肯定掺了假.在铁的事实面前,金匠不得不低头承认,王冠里确实掺了白银.烦人的王冠之谜终于解开了.
小明受阿基米德测皇冠的故事的启发,想要做以下的一个探究:
小明准备了一个长方体的无盖容器和A,B两种型号的钢球若干.先往容器里加入一定量的水,如图,水高度为30mm,水足以淹没所有的钢球.
探究一:小明做了两次实验,先放入3个A型号钢球,水面的高度涨到36mm;把3个A型号钢球捞出,再放入2个B型号钢球,水面的高度恰好也涨到36mm.
由此可知A型号与B型号钢球的体积比为 2:3 ;
探究二:小明把之前的钢球全部捞出,然后再放入A型号与B型号钢球共10个后,水面高度涨到57mm,问放入水中的A型号与B型号钢球各几个?
【分析】探究一:依据3个A型号钢球与2个B型号钢球的体积相等,即可得到A型号与B型号钢球的体积比为2:3;
探究二:设放入水中的A型号钢球为x个,则B型号钢球为(10﹣x)个,则由放入A型号与B型号钢球共10个后,水面高度涨到57mm,可得方程,进而得出结论.
【解答】解:探究一:
由题可得,3个A型号钢球与2个B型号钢球的体积相等,
∴A型号与B型号钢球的体积比为2:3;
故答案为:2:3;
探究二:
每个A型号钢球使得水面上升(36﹣30)=2 mm,
每个B型号钢球使得水面上升(36﹣30)=3mm,
设放入水中的A型号钢球为x个,则B型号钢球为(10﹣x)个,则由题意列方程:
2x+3(10﹣x)=57﹣30,
解得:x=3,
所以10﹣x=7,
答:放入水中的A型号钢球3个,B型号钢球7个.
【点评】本题主要考查了一元一次方程的应用,解决问题的关键是依据等量关系列方程求解.
20.由如图所示的图形绕虚线旋转一周得到的几何体有多少个面?其中多少个是平面?多少个是曲面?
【分析】根据面动成体,即可得到由三个圆柱组成的几何体.
【解答】解:由如图所示的图形绕虚线旋转一周得到的几何体由三个圆柱组成,
∴有7个面,其中4个是平面,3个是曲面.
【点评】本题主要考查了点、线、面、体,从运动的观点来看,点动成线,线动成面,面动成体.点、线、面、体组成几何图形.
21.一个长方体长、宽、高分别为4厘米、2厘米和1厘米.
(1)小明用斜二测画法画这个长方体的直观图时,长画4厘米,宽画 1 厘米,高画1厘米;
(2)如果用一根细铁丝做成这个长方体架子,不计材料损耗,至少需要多少厘米的铁丝?
(3)如果用8个这样相同的小长方体拼成一个正方体,那么此正方体的表面积是多少平方厘米?
【分析】(1)根据平行于x轴的线段的长度不变,而平行于y轴的线段的长度变为原来的一半,即可得到结论;
(2)根据长方体的棱长之和,即可得到铁丝的长度;
(3)根据正方体的体积得到其棱长,进而得到其表面积.
【解答】解:(1)几何体的直观图中,平行于x轴的线段的长度不变,而平行于y轴的线段的长度变为原来的一半,故宽画1厘米;
故答案为:1;
(2)4(4+2+1)=28(厘米),
故至少需要28厘米的铁丝;
(3)用8个这样相同的小长方体拼成一个正方体,其体积为8×4×2×1=64(立方厘米),故其棱长为4厘米,
∴此正方体的表面积是6×4×4=96(平方厘米).
【点评】本题主要考查了几何体的表面积,解题时注意:长方体表面积=2(ab+ah+bh)(a为长方体的长,b为长方体的宽,h为长方体的高);正方体表面积=6a2 (a为正方体棱长).
22.如图是一个长方体的表面展开图,每个面都标注了字母,现在要把它折成长方体,并使F在前面,D面在右面,那么哪一个面会在上面?
【分析】这是一个正方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,“C”与面“E”相对.利用长方体及其表面展开图的特点解题.
【解答】解:由图可知,面“A”与面“F”相对,面“B”与面“D”相对,“C”与面“E”相对,
如果“F”面在前面,“D”面在右面,那么“E”面在下面,“A”面在后面,“B”面在左面,
故“C”面会在上面(字母朝外).
【点评】本题考查了几何体的展开图,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
23.如图是一颗骰子的三种不同的放置方法.
(1)根据图中三种放置方法,推出“?”处的点数.
(2)求这三个骰子下底面上点数和.
【分析】(1)由左侧两个图形可得,与2相邻的面为3,4,5,6,由第一个和第三个图可得,与6相邻的面为2,4,5,据此可得结论;
(2)由第一个图可知,4的对面是5,即可得到第二个图和第三个图的下底面都为5,进而得出这三个骰子下底面上点数和.
【解答】解:(1)由左侧两个图形可得,与2相邻的面为3,4,5,6,
故2的对面是1,即第一个图的下底面为1,
又由第一个和第三个图可得,与6相邻的面为2,4,5,
故第一个图的左面是4,后面为3,
故结合第一个和第三个图可得“?”处的点数为2.
(2)由第一个图可知,4的对面是5,
故第二个图和第三个图的下底面都为5,
故这三个骰子下底面上点数和为5+5+1=11.
【点评】本题主要考查学生的空间想象能力和推理能力.注意正方体的空间图形,从相对面入手,分析及解答问题.
24.由7个相同的小立方块搭成的几何体如图所示,
(1)请画出它的三视图?
(2)请计算它的表面积?(棱长为1)
【分析】(1)主视图从左往右3列正方形的个数依次为2,1,2;左视图从左往右2列正方形的个数依次为2,1;俯视图从左往右3列正方形的个数依次为2,2,1,依此画出图形即可;
(2)查出从前后,上下,左右可以看到的面,然后再加上中间空两边的两个正方形的2个面,进行计算即可求解.
【解答】解:(1)如图所示:
(2)从正面看,有5个面,从后面看有5个面,
从上面看,有5个面,从下面看,有5个面,
从左面看,有3个面,从右面看,有3个面,
中间空处的两边两个正方形有2个面,
∴表面积为(5+5+3)×2+2=26+2=28.
【点评】考查画几何体的三视图;用到的知识点为:主视图,左视图分别是从物体的正面,左面看得到的图形,(2)中要注意中加空处的两边的两个正方形的两个面也是表面积的一部分,容易漏掉而导致出错.
25.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
【分析】(1)由俯视图可得该几何体有2行,则左视图应有2列,由主视图可得共有3层,那么其中一列必为3个正方形,另一列最少是1个,最多是3个;
(2)由俯视图可得该组合几何体有3列,2行,以及最底层正方体的个数及摆放形状,由主视图结合俯视图可得从左边数第二列第二层最少有1个正方体,最多有2个正方体,第3列第2层,最少有1个正方体,最多有2个正方体,第3层最少有1个正方体,最多有2个正方体,分别相加得到组成组合几何体的最少个数及最多个数即可得到n的可能的值.
【解答】解:(1)
(2)∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;
由主视图可得第2层最多有4个正方体,第3层最多有2个正方体;
∴该组合几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,
∴n可能为8或9或10或11.
【点评】考查由视图判断几何体;用到的知识点为:俯视图中正方形的个数是组合几何体最底层正方体的个数;组合几何体的最少个数是底层的正方体数加上主视图中第二层和第3层正方形的个数.
26.已知一个几何体的三视图如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1cm2)
【分析】有2个视图为长方形可得该几何体为柱体,由第3个视图为直角三角形可得该几何体的具体形状,表面积为2个直角边长为30cm的等腰直角三角形的面积加上2个边长为50cm,30cm的长方形的面积加上1个边长为30,50的长方形的面积,把相关数值代入计算即可.
【解答】解:∵有2个视图为长方形,
∴该几何体为柱体,
∵第3个视图为直角三角形,
∴该柱体为直三棱柱;
∵直角三角形斜边长为:=30cm,
∴表面积为2××30×30+2×50×30+50×30≈6021cm2.
【点评】考查由视图判断几何体及几何体表面积的计算;用到的知识点为:有2个视图是长方形的几何体为柱体;得到三棱柱的组成部分的边长是解决本题的关键.
一.选择题(共10小题)
1.一个长方形的长和宽分别为3cm和2cm,依次以这个长方形的长和宽所在的直线为旋转轴,把长方形旋转1周形成圆柱体甲和圆柱体乙,两个圆柱体的体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙 B.V甲>V乙,S甲=S乙
C.V甲=V乙,S甲=S乙 D.V甲>V乙,S甲<S乙
2.下列4个平面图形中,哪一个是由图中正方体纸盒展开得到的( )
A. B.
C. D.
3.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A. B.
C. D.
4.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
C. D.
5.如图,在一个正方形盒子的六面上写有“祝、母、校、更、美、丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向)不可能的是( )
A. B.
C. D.
6.如图,小明从左面看在水平讲台上放置的圆柱形水杯和长方体形粉笔盒看到的是( )
A. B. C. D.
7.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
8.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )
A.10 B.12 C.15 D.18
9.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是( )个小立方块搭成的
A.8 B.7 C.6 D.5
10.一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积是( )
A.6π B.4π C.8π D.4
二.填空题(共8小题)
11.把一个长为20πcm、宽16πcm的长方形围成圆柱的侧面,则圆柱的底面半径是 cm.
12.将一个长4cm宽2cm的长方形绕它的一边所在的直线旋转一周,所得几何体的体积为 cm3.
13.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走 个小立方块.
14.某种无盖的长方体包装盒的展开图如图所示.根据图中数据计算,这种药品包装盒的体积是 .
15.如图,是一个四棱锥及它的三视图,其中,图 是它的主视图,图 是它的左视图,图 是它的俯视图.
16.用小正方体搭一个几何体,其主视图和左视图如图所示,那么搭成这样的几何体至少需要 个小正方体,最多需要 个小正方体.
17.用若干个体积为1的正方体搭成一个几何体,该几何体正视(从正面看)与俯视(从上面垂直向下看)都是如图所示的图形,则这个几何体的最大体积是 .
18.如图是一个几何体的三视图,根据图中标注的数据可求出这个几何体的体积为 .
三.解答题(共8小题)
19.先阅读,然后答题.
阿基米德测皇冠的故事
叙古拉国王艾希罗交给金匠一块黄金,让他做一顶王冠.王冠做成后,国王拿在手里觉得有点轻.他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿秤来称,结果与原来的金块一样重.国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题.回家后,阿基米德闭门谢客,冥思苦想,但百思不得其解.一天,他的夫人逼他洗澡.当他跳入池中时,水从池中溢了出来.阿基米德听到那哗哗哗的流水声,灵感一下子冒了出来.他从池中跳出来,连衣服都没穿,就冲到街上,高喊着:“优勒加!优勒加!(意为发现了)“.夫人这回可真着急了,嘴里嘟囔着“真疯了,真疯了“,便随后追了出去.街上的人不知发生了什么事,也都跟在后面追着看.原来,阿基米德由澡盆溢水找到了解决王冠问题的办法:相同质量的相同物质泡在水里,溢出的水的体积应该相同.如果把王冠放到水了,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假.阿基为德跑到王宫后立即找来一盆水,又找来同样重量的一块黄金,一块白银,分两次泡进盆里,白银溢出的水比黄金溢出的几乎要多一倍,然后他又把王冠和金块分别泡进水盆里,王冠溢出的水比金块多,显然王冠的质量不等于金块的质量,王冠里肯定掺了假.在铁的事实面前,金匠不得不低头承认,王冠里确实掺了白银.烦人的王冠之谜终于解开了.
小明受阿基米德测皇冠的故事的启发,想要做以下的一个探究:
小明准备了一个长方体的无盖容器和A,B两种型号的钢球若干.先往容器里加入一定量的水,如图,水高度为30mm,水足以淹没所有的钢球.
探究一:小明做了两次实验,先放入3个A型号钢球,水面的高度涨到36mm;把3个A型号钢球捞出,再放入2个B型号钢球,水面的高度恰好也涨到36mm.
由此可知A型号与B型号钢球的体积比为 ;
探究二:小明把之前的钢球全部捞出,然后再放入A型号与B型号钢球共10个后,水面高度涨到57mm,问放入水中的A型号与B型号钢球各几个?
20.由如图所示的图形绕虚线旋转一周得到的几何体有多少个面?其中多少个是平面?多少个是曲面?
21.一个长方体长、宽、高分别为4厘米、2厘米和1厘米.
(1)小明用斜二测画法画这个长方体的直观图时,长画4厘米,宽画 厘米,高画1厘米;
(2)如果用一根细铁丝做成这个长方体架子,不计材料损耗,至少需要多少厘米的铁丝?
(3)如果用8个这样相同的小长方体拼成一个正方体,那么此正方体的表面积是多少平方厘米?
22.如图是一个长方体的表面展开图,每个面都标注了字母,现在要把它折成长方体,并使F在前面,D面在右面,那么哪一个面会在上面?
23.如图是一颗骰子的三种不同的放置方法.
(1)根据图中三种放置方法,推出“?”处的点数.
(2)求这三个骰子下底面上点数和.
24.由7个相同的小立方块搭成的几何体如图所示,
(1)请画出它的三视图?
(2)请计算它的表面积?(棱长为1)
25.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
26.已知一个几何体的三视图如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1cm2)
2020年北师大版七年级上册数学《第1章 丰富的图形世界》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.一个长方形的长和宽分别为3cm和2cm,依次以这个长方形的长和宽所在的直线为旋转轴,把长方形旋转1周形成圆柱体甲和圆柱体乙,两个圆柱体的体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙 B.V甲>V乙,S甲=S乙
C.V甲=V乙,S甲=S乙 D.V甲>V乙,S甲<S乙
【分析】根据圆柱体的体积=底面积×高求解,再利用圆柱体侧面积求法得出答案.
【解答】解:由题可得,
V甲=π?22×3=12π,
V乙=π?32×2=18π,
∵12π<18π,
∴V甲<V乙;
∵S甲=2π×2×3=12π,
S乙=2π×3×2=12π,
∴S甲=S乙,
故选:A.
【点评】此题主要考查了面动成体,关键是掌握圆柱体的体积和侧面积计算公式.
2.下列4个平面图形中,哪一个是由图中正方体纸盒展开得到的( )
A. B.
C. D.
【分析】在验证立方体的展开图时,要细心观察每一个标志的位置是否一致,然后进行判断.
【解答】解:把四个选项的展开图折叠,能复原的是C.
故选:C.
【点评】本题考查正方体的表面展开图及空间想象能力.易错易混点:学生对相关图的位置想象不准确,从而错选,解决这类问题时,不妨动手实际操作一下,即可解决问题.
3.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A. B.
C. D.
【分析】三棱柱的侧面展开图是长方形,底面是三角形,据此进行判断即可.
【解答】解:A选项中,展开图下方的直角三角形的斜边长为12,不合题意;
B选项中,展开图上下两个直角三角形中的直角边不能与其它棱完全重合,不合题意;
C选项中,展开图下方的直角三角形中的直角边不能与其它棱完全重合,不合题意;
D选项中,展开图能折叠成一个三棱柱,符合题意;
故选:D.
【点评】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
4.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
C. D.
【分析】根据长方体的组成,通过结合立体图形与平面图形的相互转化,分别分析得出即可.
【解答】解:A、剪去阴影部分后,能组成长方体,故此选项正确;
B、剪去阴影部分后,无法组成长方体,故此选项不合题意;
C、剪去阴影部分后,组成无盖的正方体,故此选项不合题意;
D、剪去阴影部分后,无法组成长方体,故此选项不合题意;
故选:A.
【点评】此题主要考查了展开图折叠成几何体,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
5.如图,在一个正方形盒子的六面上写有“祝、母、校、更、美、丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向)不可能的是( )
A. B.
C. D.
【分析】根据立方体的平面展开图规律解决问题即可.
【解答】解:由图可得,“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图可能是A,B,C选项,
而D选项中,“更”与“祝”的位置有误,互换后则符合题意.
故选:D.
【点评】本题主要考查了正方体的展开图,对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
6.如图,小明从左面看在水平讲台上放置的圆柱形水杯和长方体形粉笔盒看到的是( )
A. B. C. D.
【分析】先细心观察原立体图形中圆柱和长方体的位置关系,找到从左面看所得到的图形即可.
【解答】解:圆柱的左视图是长方形,长方体的左视图是长方形,所以它们的左视图是:
故选:D.
【点评】考查简单组合体的三视图,解题时注意:左视图是从物体的左面看得到的视图.要注意几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线化成虚线.
7.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【解答】解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故选:C.
【点评】本题考查的是三视图的知识以及学生对该知识点的巩固.解题关键是找到三种视图的正方形的个数.
8.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )
A.10 B.12 C.15 D.18
【分析】拿掉若干个小立方块后保证几何体不倒掉,且三个视图仍都为3×3的正方形,所以最底下一层必须有9个小立方块,这样能保证俯视图仍为3×3的正方形,为保证正视图与左视图也为3×3的正方形,所以上面两层必须保留底面上一条对角线方向的三个立方块,即可得到最多能拿掉小立方块的个数.
【解答】解:根据题意,拿掉若干个小立方块后,三个视图仍都为3×3的正方形,
则最多能拿掉小立方块的个数为6+6=12个.
故选:B.
【点评】本题考查了几何体的三种视图,解决此类图的关键是由立体图形得到三视图.
9.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是( )个小立方块搭成的
A.8 B.7 C.6 D.5
【分析】根据题意可以得到该几何体从正面和上面看至少有多少个小立方体,综合考虑即可解答本题.
【解答】解:根据主视图可得,俯视图中第一列中至少一处有2层;
所以该几何体至少是用6个小立方块搭成的.
故选:C.
【点评】本题考查了由三视图判断几何体,由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
10.一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积是( )
A.6π B.4π C.8π D.4
【分析】根据题意,可判断出该几何体为圆柱.且已知底面半径以及高,易求表面积.
【解答】解:根据题目的描述,可以判断出这个几何体应该是个圆柱,且它的底面圆的半径为1,高为2,
那么它的表面积=2π×2+π×1×1×2=6π,故选:A.
【点评】本题要判断出几何体的形状然后再根据其面积公式进行计算,注意本题中的圆柱有上下底,不要漏掉任何一个.
二.填空题(共8小题)
11.把一个长为20πcm、宽16πcm的长方形围成圆柱的侧面,则圆柱的底面半径是 10或8 cm.
【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,或者长方形的宽等于底面周长,长等于圆柱的高,从而可以求出底面积半径.
【解答】解:分两种情况:
①20π÷(2×π)=10(cm),
故底面圆的半径为10cm,
②16π÷(2×π)=8(cm),
故底面圆的半径为8cm,
故答案为:10或8.
【点评】本题主要考查了立体图形,解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高.
12.将一个长4cm宽2cm的长方形绕它的一边所在的直线旋转一周,所得几何体的体积为 16π或32π cm3.
【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
【解答】解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).
故它们的体积分别为16πcm3或32πcm3.
故答案为:16π或32π.
【点评】本题考查圆柱体的体积的求法,注意分情况讨论.从运动的观点来看,点动成线,线动成面,面动成体.
13.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走 16 个小立方块.
【分析】根据表面积不变,只需留11个,分别是正中心的3个和四角上各2个.
【解答】解:若新几何体与原正方体的表面积相等,最多可以取走16个小正方体,只需留11个,分别是正中心的3个和四角上各2个,如图所示:
故答案为:16
【点评】本题主要考查了几何体的表面积.
14.某种无盖的长方体包装盒的展开图如图所示.根据图中数据计算,这种药品包装盒的体积是 180 .
【分析】先求出无盖长方体盒子的长、宽、高,再根据长方体的容积公式求出盒子的体积.
【解答】解:观察图形可知长方体盒子的高=12﹣9=3,宽=12﹣3×2=6,长=16﹣6=10,
则盒子的体积=3×10×6=180.
故答案为:180.
【点评】本题考查了几何体的展开图,正确理解无盖长方体的展开图,与原来长方体的之间的关系是解决本题的关键,长方体的容积=长×宽×高.
15.如图,是一个四棱锥及它的三视图,其中,图 C 是它的主视图,图 A 是它的左视图,图 B 是它的俯视图.
【分析】从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,根据三视图的概念判断即可.
【解答】解:从上面看四棱锥是一长方形加两条对角线,那么B是俯视图;由俯视图易得从正面看四棱锥是一个底边较大的三角形,故选C;从左面看四棱锥是一个底边较小的三角形,故选A.
【点评】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意所有看到的棱与顶点在三视图中都得表现出来.
16.用小正方体搭一个几何体,其主视图和左视图如图所示,那么搭成这样的几何体至少需要 5 个小正方体,最多需要 13 个小正方体.
【分析】根据图形,主视图的底层最多有9个小正方体,最少有3个小正方形.第二层最多有4个小正方形,最少有2个小正方形.
【解答】解:综合主视图和左视图,这个几何体的底层最多有3×3=9个小正方体,最少有3个小正方体,第二层最多有4个小正方体,最少有2个小正方体,那么搭成这样的几何体至少需要3+2=5个小正方体,最多需要4+9=13个小正方体.故答案为5个,13个.
【点评】本题要分别对最多和最少两种情况进行讨论,然后根据“俯视图打地基,正视图疯狂盖,左视图拆违章”来分析出小正方体的个数.
17.用若干个体积为1的正方体搭成一个几何体,该几何体正视(从正面看)与俯视(从上面垂直向下看)都是如图所示的图形,则这个几何体的最大体积是 11 .
【分析】由正视图、侧视图可知,体积最大时,俯视图中中间一列各个位置都有3个,两侧各1个,据此可得这个几何体的最大体积.
【解答】解:由正视图、侧视图可知,体积最大时,俯视图中中间一列各个位置都有3个,两侧各1个,共11个,
故这个几何体的最大体积是11.
故答案为:11.
【点评】本题主要考查了由三视图判断几何体,由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
18.如图是一个几何体的三视图,根据图中标注的数据可求出这个几何体的体积为 24π .
【分析】易得此几何体为圆柱,圆柱的体积=底面积×高,把相关数值代入即可求解.
【解答】解:此几何体为圆柱,体积为π×22×6=24π.
【点评】解决本题的关键是得到此几何体的形状,易错点是得到计算此几何体所需要的相关数据.
三.解答题(共8小题)
19.先阅读,然后答题.
阿基米德测皇冠的故事
叙古拉国王艾希罗交给金匠一块黄金,让他做一顶王冠.王冠做成后,国王拿在手里觉得有点轻.他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿秤来称,结果与原来的金块一样重.国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题.回家后,阿基米德闭门谢客,冥思苦想,但百思不得其解.一天,他的夫人逼他洗澡.当他跳入池中时,水从池中溢了出来.阿基米德听到那哗哗哗的流水声,灵感一下子冒了出来.他从池中跳出来,连衣服都没穿,就冲到街上,高喊着:“优勒加!优勒加!(意为发现了)“.夫人这回可真着急了,嘴里嘟囔着“真疯了,真疯了“,便随后追了出去.街上的人不知发生了什么事,也都跟在后面追着看.原来,阿基米德由澡盆溢水找到了解决王冠问题的办法:相同质量的相同物质泡在水里,溢出的水的体积应该相同.如果把王冠放到水了,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假.阿基为德跑到王宫后立即找来一盆水,又找来同样重量的一块黄金,一块白银,分两次泡进盆里,白银溢出的水比黄金溢出的几乎要多一倍,然后他又把王冠和金块分别泡进水盆里,王冠溢出的水比金块多,显然王冠的质量不等于金块的质量,王冠里肯定掺了假.在铁的事实面前,金匠不得不低头承认,王冠里确实掺了白银.烦人的王冠之谜终于解开了.
小明受阿基米德测皇冠的故事的启发,想要做以下的一个探究:
小明准备了一个长方体的无盖容器和A,B两种型号的钢球若干.先往容器里加入一定量的水,如图,水高度为30mm,水足以淹没所有的钢球.
探究一:小明做了两次实验,先放入3个A型号钢球,水面的高度涨到36mm;把3个A型号钢球捞出,再放入2个B型号钢球,水面的高度恰好也涨到36mm.
由此可知A型号与B型号钢球的体积比为 2:3 ;
探究二:小明把之前的钢球全部捞出,然后再放入A型号与B型号钢球共10个后,水面高度涨到57mm,问放入水中的A型号与B型号钢球各几个?
【分析】探究一:依据3个A型号钢球与2个B型号钢球的体积相等,即可得到A型号与B型号钢球的体积比为2:3;
探究二:设放入水中的A型号钢球为x个,则B型号钢球为(10﹣x)个,则由放入A型号与B型号钢球共10个后,水面高度涨到57mm,可得方程,进而得出结论.
【解答】解:探究一:
由题可得,3个A型号钢球与2个B型号钢球的体积相等,
∴A型号与B型号钢球的体积比为2:3;
故答案为:2:3;
探究二:
每个A型号钢球使得水面上升(36﹣30)=2 mm,
每个B型号钢球使得水面上升(36﹣30)=3mm,
设放入水中的A型号钢球为x个,则B型号钢球为(10﹣x)个,则由题意列方程:
2x+3(10﹣x)=57﹣30,
解得:x=3,
所以10﹣x=7,
答:放入水中的A型号钢球3个,B型号钢球7个.
【点评】本题主要考查了一元一次方程的应用,解决问题的关键是依据等量关系列方程求解.
20.由如图所示的图形绕虚线旋转一周得到的几何体有多少个面?其中多少个是平面?多少个是曲面?
【分析】根据面动成体,即可得到由三个圆柱组成的几何体.
【解答】解:由如图所示的图形绕虚线旋转一周得到的几何体由三个圆柱组成,
∴有7个面,其中4个是平面,3个是曲面.
【点评】本题主要考查了点、线、面、体,从运动的观点来看,点动成线,线动成面,面动成体.点、线、面、体组成几何图形.
21.一个长方体长、宽、高分别为4厘米、2厘米和1厘米.
(1)小明用斜二测画法画这个长方体的直观图时,长画4厘米,宽画 1 厘米,高画1厘米;
(2)如果用一根细铁丝做成这个长方体架子,不计材料损耗,至少需要多少厘米的铁丝?
(3)如果用8个这样相同的小长方体拼成一个正方体,那么此正方体的表面积是多少平方厘米?
【分析】(1)根据平行于x轴的线段的长度不变,而平行于y轴的线段的长度变为原来的一半,即可得到结论;
(2)根据长方体的棱长之和,即可得到铁丝的长度;
(3)根据正方体的体积得到其棱长,进而得到其表面积.
【解答】解:(1)几何体的直观图中,平行于x轴的线段的长度不变,而平行于y轴的线段的长度变为原来的一半,故宽画1厘米;
故答案为:1;
(2)4(4+2+1)=28(厘米),
故至少需要28厘米的铁丝;
(3)用8个这样相同的小长方体拼成一个正方体,其体积为8×4×2×1=64(立方厘米),故其棱长为4厘米,
∴此正方体的表面积是6×4×4=96(平方厘米).
【点评】本题主要考查了几何体的表面积,解题时注意:长方体表面积=2(ab+ah+bh)(a为长方体的长,b为长方体的宽,h为长方体的高);正方体表面积=6a2 (a为正方体棱长).
22.如图是一个长方体的表面展开图,每个面都标注了字母,现在要把它折成长方体,并使F在前面,D面在右面,那么哪一个面会在上面?
【分析】这是一个正方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,“C”与面“E”相对.利用长方体及其表面展开图的特点解题.
【解答】解:由图可知,面“A”与面“F”相对,面“B”与面“D”相对,“C”与面“E”相对,
如果“F”面在前面,“D”面在右面,那么“E”面在下面,“A”面在后面,“B”面在左面,
故“C”面会在上面(字母朝外).
【点评】本题考查了几何体的展开图,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
23.如图是一颗骰子的三种不同的放置方法.
(1)根据图中三种放置方法,推出“?”处的点数.
(2)求这三个骰子下底面上点数和.
【分析】(1)由左侧两个图形可得,与2相邻的面为3,4,5,6,由第一个和第三个图可得,与6相邻的面为2,4,5,据此可得结论;
(2)由第一个图可知,4的对面是5,即可得到第二个图和第三个图的下底面都为5,进而得出这三个骰子下底面上点数和.
【解答】解:(1)由左侧两个图形可得,与2相邻的面为3,4,5,6,
故2的对面是1,即第一个图的下底面为1,
又由第一个和第三个图可得,与6相邻的面为2,4,5,
故第一个图的左面是4,后面为3,
故结合第一个和第三个图可得“?”处的点数为2.
(2)由第一个图可知,4的对面是5,
故第二个图和第三个图的下底面都为5,
故这三个骰子下底面上点数和为5+5+1=11.
【点评】本题主要考查学生的空间想象能力和推理能力.注意正方体的空间图形,从相对面入手,分析及解答问题.
24.由7个相同的小立方块搭成的几何体如图所示,
(1)请画出它的三视图?
(2)请计算它的表面积?(棱长为1)
【分析】(1)主视图从左往右3列正方形的个数依次为2,1,2;左视图从左往右2列正方形的个数依次为2,1;俯视图从左往右3列正方形的个数依次为2,2,1,依此画出图形即可;
(2)查出从前后,上下,左右可以看到的面,然后再加上中间空两边的两个正方形的2个面,进行计算即可求解.
【解答】解:(1)如图所示:
(2)从正面看,有5个面,从后面看有5个面,
从上面看,有5个面,从下面看,有5个面,
从左面看,有3个面,从右面看,有3个面,
中间空处的两边两个正方形有2个面,
∴表面积为(5+5+3)×2+2=26+2=28.
【点评】考查画几何体的三视图;用到的知识点为:主视图,左视图分别是从物体的正面,左面看得到的图形,(2)中要注意中加空处的两边的两个正方形的两个面也是表面积的一部分,容易漏掉而导致出错.
25.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
【分析】(1)由俯视图可得该几何体有2行,则左视图应有2列,由主视图可得共有3层,那么其中一列必为3个正方形,另一列最少是1个,最多是3个;
(2)由俯视图可得该组合几何体有3列,2行,以及最底层正方体的个数及摆放形状,由主视图结合俯视图可得从左边数第二列第二层最少有1个正方体,最多有2个正方体,第3列第2层,最少有1个正方体,最多有2个正方体,第3层最少有1个正方体,最多有2个正方体,分别相加得到组成组合几何体的最少个数及最多个数即可得到n的可能的值.
【解答】解:(1)
(2)∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;
由主视图可得第2层最多有4个正方体,第3层最多有2个正方体;
∴该组合几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,
∴n可能为8或9或10或11.
【点评】考查由视图判断几何体;用到的知识点为:俯视图中正方形的个数是组合几何体最底层正方体的个数;组合几何体的最少个数是底层的正方体数加上主视图中第二层和第3层正方形的个数.
26.已知一个几何体的三视图如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1cm2)
【分析】有2个视图为长方形可得该几何体为柱体,由第3个视图为直角三角形可得该几何体的具体形状,表面积为2个直角边长为30cm的等腰直角三角形的面积加上2个边长为50cm,30cm的长方形的面积加上1个边长为30,50的长方形的面积,把相关数值代入计算即可.
【解答】解:∵有2个视图为长方形,
∴该几何体为柱体,
∵第3个视图为直角三角形,
∴该柱体为直三棱柱;
∵直角三角形斜边长为:=30cm,
∴表面积为2××30×30+2×50×30+50×30≈6021cm2.
【点评】考查由视图判断几何体及几何体表面积的计算;用到的知识点为:有2个视图是长方形的几何体为柱体;得到三棱柱的组成部分的边长是解决本题的关键.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
