2020年北师大版七年级上册数学《第3章 整式及其加减》单元测试卷(解析版)
文档属性
| 名称 | 2020年北师大版七年级上册数学《第3章 整式及其加减》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 14:04:18 | ||
图片预览




文档简介
2020年北师大版七年级上册数学《第3章 整式及其加减》单元测试卷
一.选择题(共10小题)
1.若a是有理数,那么在①a+1,②|a+1|,③|a|+1,④a2+1中,一定是正数的有( )
A.1个 B.2个 C.3个 D.4个
2.为参加“爱我校园”摄影赛,小明同学将参与植树活动的照片放大为长acm,宽acm的形状,又精心在四周加上了宽2cm的木框,则这幅摄影作品占的面积是( )cm2.
A. a2﹣a+4 B. a2﹣7a+16 C. a2+a+4 D. a2+7a+16
3.如果2x﹣y=3,那么代数式4﹣2x+y的值为( )
A.﹣1 B.4 C.﹣4 D.1
4.下列运算正确的是( )
A.5xy﹣4xy=1 B.3x2+2x3=5x5
C.x2﹣x=x D.3x2+2x2=5x2
5.已知一列数,a1=,a2=,a3=,a4=…,当a0=3时,则a2018等于( )
A.3 B.﹣2 C. D.
6.若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有( )个.
A.5 B.4 C.3 D.2
7.有7个如图①的长为x,宽为y(x>y)的小长方形,按图②的方式不重叠的放在长方形ABCD中,未被覆盖的部分用阴影表示,若右下角阴影部分的面积S2与左上角阴影部分的面积S1之差为S,当BC的长度变化时,按照相同的放置方式,S始终保持不变,则x与y满足的关系式为( )
A.x=3y B.x=3y+1 C.x=2y D.x=2y+1
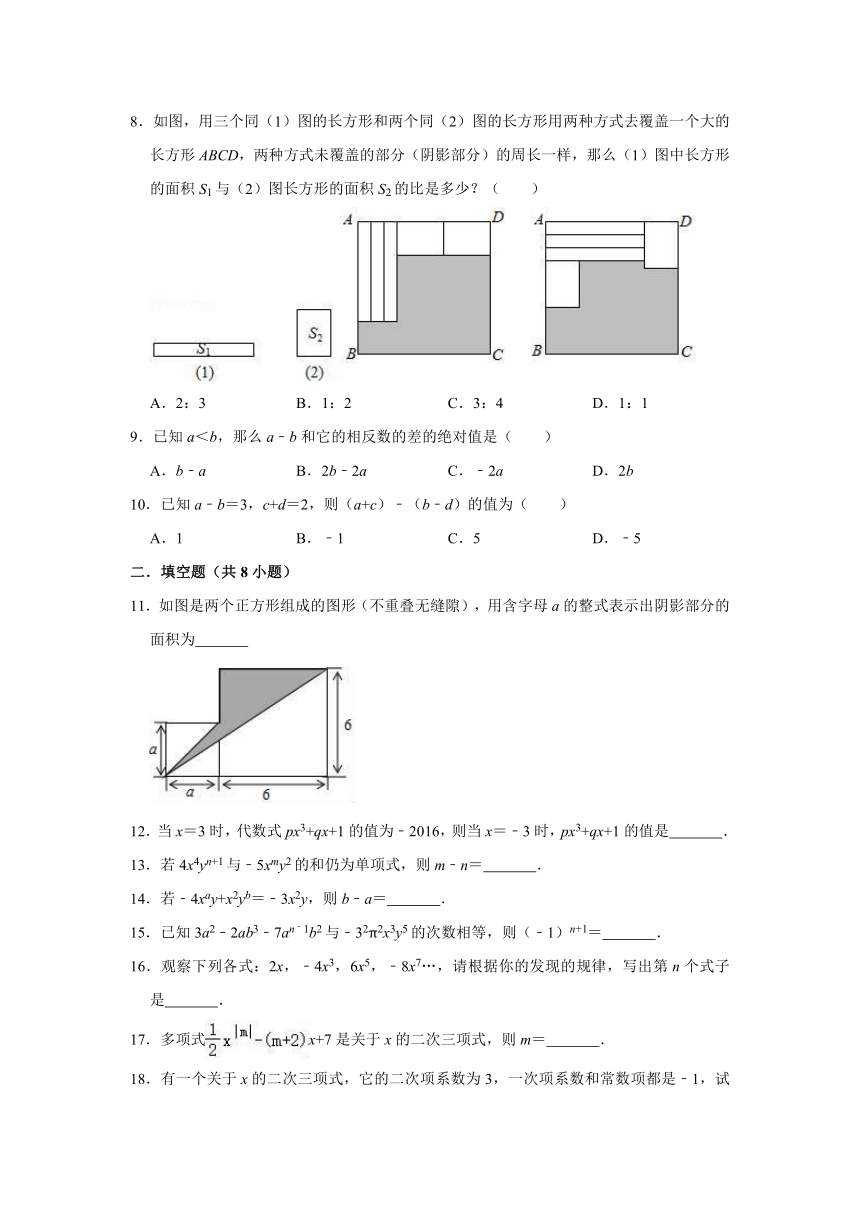
8.如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积S1与(2)图长方形的面积S2的比是多少?( )
A.2:3 B.1:2 C.3:4 D.1:1
9.已知a<b,那么a﹣b和它的相反数的差的绝对值是( )
A.b﹣a B.2b﹣2a C.﹣2a D.2b
10.已知a﹣b=3,c+d=2,则(a+c)﹣(b﹣d)的值为( )
A.1 B.﹣1 C.5 D.﹣5
二.填空题(共8小题)
11.如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为
12.当x=3时,代数式px3+qx+1的值为﹣2016,则当x=﹣3时,px3+qx+1的值是 .
13.若4x4yn+1与﹣5xmy2的和仍为单项式,则m﹣n= .
14.若﹣4xay+x2yb=﹣3x2y,则b﹣a= .
15.已知3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,则(﹣1)n+1= .
16.观察下列各式:2x,﹣4x3,6x5,﹣8x7…,请根据你的发现的规律,写出第n个式子是 .
17.多项式x+7是关于x的二次三项式,则m= .
18.有一个关于x的二次三项式,它的二次项系数为3,一次项系数和常数项都是﹣1,试写出这个多项式 .
三.解答题(共8小题)
19.某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家6月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
20.当x=1,y=﹣6时,求下列代数式的值.
(1)x2+y2
(2)(x+y)2
(3)x2﹣2xy+y2.
21.阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛尝试应用
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是 ;
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值 .
22.先去括号、再合并同类项
①2(a﹣b+c)﹣3(a+b﹣c)
②3a2b﹣2[ab2﹣2(a2b﹣2ab2)].
23.已知g(﹣1)=g(4)=0,g(﹣3)=,g(﹣2)=2,试求三次多项式g(x)的表达式.
24.计算:
(1)3y2﹣2y+4y2
(2)st+4﹣3st﹣4;
(3)2(2ab+3a)﹣3(2a﹣ab);
(4)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.
(5)(﹣1)3﹣(1﹣)÷3×[3﹣(﹣3)2].
(6)7×1÷(﹣9+19);
(7)﹣24×(﹣+﹣);
(8)(﹣81)÷2+÷(﹣16);
25.如图,已知a、b、c在数轴上的位置,求|b+c|﹣|a﹣b|﹣|c﹣b|的值.
26.计算
(1)3+(﹣)﹣()+2
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣)2
(3)(3a﹣2)+3(5﹣a)﹣13
(4)||+||+||+…+||
2020年北师大版七年级上册数学《第3章 整式及其加减》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.若a是有理数,那么在①a+1,②|a+1|,③|a|+1,④a2+1中,一定是正数的有( )
A.1个 B.2个 C.3个 D.4个
【分析】通过给a一数值,举反例,排除法求解.
【解答】解:①a=﹣2时,a+1=﹣1是负数;②a=﹣1时,|a+1|=0不是正数;不论a取何值,都有|a|+1≥1、a2+1≥1;
所以一定是正数的有③|a|+1,④a2+1;故选B.
【点评】本题考查知识点为:一个数的绝对值和一个数的平方一定是非负数,所以加上一个正数后则一定是正数.
2.为参加“爱我校园”摄影赛,小明同学将参与植树活动的照片放大为长acm,宽acm的形状,又精心在四周加上了宽2cm的木框,则这幅摄影作品占的面积是( )cm2.
A. a2﹣a+4 B. a2﹣7a+16 C. a2+a+4 D. a2+7a+16
【分析】此题涉及面积公式的运用,解答时直接运用面积的公式求出答案.
【解答】解:根据题意可知,
这幅摄影作品占的面积是a2+4(a+4)+4(a+4)﹣4×4=a2+7a+16.
故选:D.
【点评】列代数式的关键是正确理解文字语言中的关键词,找到其中的数量关系列出式子.
3.如果2x﹣y=3,那么代数式4﹣2x+y的值为( )
A.﹣1 B.4 C.﹣4 D.1
【分析】将2x﹣y的值整体代入到4﹣2x+y=4﹣(2x﹣y)即可.
【解答】解:当2x﹣y=3时,
4﹣2x+y=4﹣(2x﹣y)=4﹣3=1,
故选:D.
【点评】本题主要考查代数式的求值,运用整体代入思想是解题的关键.
4.下列运算正确的是( )
A.5xy﹣4xy=1 B.3x2+2x3=5x5
C.x2﹣x=x D.3x2+2x2=5x2
【分析】区分是否是同类项,在根据合并同类项的法则合并即可.
【解答】解:A、5xy﹣4xy=xy,故本选项错误;
B、不是同类项,不能合并,故本选项错误;
C、不是同类项,不能合并,故本选项错误;
D、3x2+2x2=5x2,故本选项正确;
故选:D.
【点评】本题考查了同类项和合并同类项等知识点的应用,同类项是指所含字母相同,并且相同字母的指数分别相等的项;同类项的系数相加,字母和字母的指数不变.
5.已知一列数,a1=,a2=,a3=,a4=…,当a0=3时,则a2018等于( )
A.3 B.﹣2 C. D.
【分析】根据数字的变化类寻找规律即可求解.
【解答】解:当a0=3时,
a1=﹣2,a2=,a3=,a4=3,
a5=﹣2,a6=…
∵2018÷4=504…2
∴a2018=.
故选:C.
【点评】本题考查了数字的变化类,解决本题的关键是通过计算寻找规律.
6.若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有( )个.
A.5 B.4 C.3 D.2
【分析】多项式相减,也就是合并同类项,合并同类项时只是把系数相加减,字母和字母的指数不变,所以结果的次数一定不高于2次,由此可以判定正确个数.
【解答】解:∵多项式相减,也就是合并同类项,
而合并同类项时只是把系数相加减,字母和字母的指数不变,
∴结果的次数一定不高于2次,
当二次项的系数相同时,合并后结果为0,
所以(1)和(2)(5)是错误的.
故选:C.
【点评】此题要准确把握合并同类项的法则,合并同类项时只是把系数相加减,字母和字母的指数不变,当二次项的系数互为相反数时,合并后结果为0.
7.有7个如图①的长为x,宽为y(x>y)的小长方形,按图②的方式不重叠的放在长方形ABCD中,未被覆盖的部分用阴影表示,若右下角阴影部分的面积S2与左上角阴影部分的面积S1之差为S,当BC的长度变化时,按照相同的放置方式,S始终保持不变,则x与y满足的关系式为( )
A.x=3y B.x=3y+1 C.x=2y D.x=2y+1
【分析】表示出左上角与右下角部分的面积,求出之差,根据差与BC无关,即与PC无关,即可求出x与y的关系式.
【解答】解:左上角阴影部分的长为AE=BP+PC﹣ED=x+PC﹣3y﹣x=PC﹣3y,宽为AF=x,右下角阴影部分的长为PC,宽CG=x+y,
∴阴影部分面积之差S=AE?AF﹣xy﹣PC?BF﹣x(x+y﹣2y)=x(PC﹣3y)﹣xy﹣PC?2y﹣x(x﹣y)=PC(x﹣2y)﹣3xy﹣x2,
则x﹣2y=0,即x=2y.
故选:C.
【点评】此题考查了整式的混合运算的应用,弄清题意是解本题的关键.
8.如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积S1与(2)图长方形的面积S2的比是多少?( )
A.2:3 B.1:2 C.3:4 D.1:1
【分析】本题需先设图(1)中长方形的长为acm,宽为bcm,图(2)中长方形的宽为xcm,长为ycm,再结合图形分别得出图形(3)的阴影周长和图形(4)的阴影周长,相等后列等式可得:a=2y,x=3b,最后根据长方形面积公式可得结论.
【解答】解:设图(1)中长方形的长为acm,宽为bcm,图(2)中长方形的宽为xcm,长为ycm,
由两个长方形ABCD的AD=3b+2y=a+x,
∴图(3)阴影部分周长为:2(3b+2y+DC﹣x)=6b+4y+2DC﹣2x=2a+2x+2DC﹣2x=2a+2DC,
∴图(4)阴影部分周长为:2(a+x+DC﹣3b)=2a+2x+2DC﹣6b=2a+2x+2DC﹣2(a+x﹣2y)=2DC+4y,
∵两种方式未覆盖的部分(阴影部分)的周长一样,
∴2a+2DC=2DC+4y,
a=2y,
∵3b+2y=a+x,
∴x=3b,
∴===,
故选:A.
【点评】本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
9.已知a<b,那么a﹣b和它的相反数的差的绝对值是( )
A.b﹣a B.2b﹣2a C.﹣2a D.2b
【分析】a﹣b的相反数是b﹣a,可得a﹣b和它的相反数为:(a﹣b)﹣(b﹣a)=2a﹣2b,又因为a<b,可知2a﹣2b<0,所以|(a﹣b)﹣(b﹣a)|=2b﹣2a.
【解答】解:依题意可得:|(a﹣b)﹣(b﹣a)|=2b﹣2a.故选B.
【点评】此题考查的是相反数的概念和整式的加减运算和绝对值的意义.
10.已知a﹣b=3,c+d=2,则(a+c)﹣(b﹣d)的值为( )
A.1 B.﹣1 C.5 D.﹣5
【分析】原式去括号整理后,将已知等式代入计算即可求出值.
【解答】解:∵a﹣b=3,c+d=2,
∴原式=a+c﹣b+d=(a﹣b)+(c+d)=3+2=5.
故选:C.
【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.
二.填空题(共8小题)
11.如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为 a2﹣3a+18.
【分析】根据面积的和差:两个正方形的面积和减去两个三角形的面积,可得答案.
【解答】解:阴影部分的面积
=a2+62﹣a2﹣(a+6)×6
=a2+36﹣a2﹣3a﹣18
=a2﹣3a+18,
故答案为: a2﹣3a+18.
【点评】本题考查了代数式求值,利用面积的和差得出关系式是解题关键.
12.当x=3时,代数式px3+qx+1的值为﹣2016,则当x=﹣3时,px3+qx+1的值是 2018 .
【分析】把x=3代入代数式,依据其值为2016,得到27p+3q的值,再将x=﹣3及27p+3q的值代入原式计算即可.
【解答】解:把x=3代入px3+qx+1,得:27p+3q=﹣2017,
则当x=﹣3时,原式=﹣27p﹣3q+1=2017+1=2018,
故答案为:2018.
【点评】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.
13.若4x4yn+1与﹣5xmy2的和仍为单项式,则m﹣n= 3 .
【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出n,m的值,再代入代数式计算即可.
【解答】解:根据题意得:m=4,n+1=2,
解得:n=1,
则m﹣n=4﹣1=3.
故答案是:3.
【点评】本题考查了同类项的定义,同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.
14.若﹣4xay+x2yb=﹣3x2y,则b﹣a= ﹣1 .
【分析】依据﹣4xay+x2yb=﹣3x2y,即可得到﹣4xay与x2yb是同类项,进而得出a,b的值.
【解答】解:∵﹣4xay+x2yb=﹣3x2y,
∴﹣4xay与x2yb是同类项,
∴,
∴b﹣a=1﹣2=﹣1,
故答案为:﹣1.
【点评】本题主要考查了同类项的定义,要掌握同类项的概念,会辨别同类项,并准确地掌握判断同类项的两条标准:带有相同系数的代数项;字母和字母指数.
15.已知3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,则(﹣1)n+1= 1 .
【分析】多项式的前两项次数分别为2、4,第三项次数为n﹣1+2,而后面单项式次数为8,故只有n﹣1+2=8.列方程可解本题.
【解答】解:∵3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,
∴n﹣1+2=8,即n+1=8.
∴(﹣1)n+1=1.
【点评】多项式里次数最高项的次数叫做这个多项式的次数.单项式中,所有字母的指数和叫做这个单项式的次数.注意π是数字因数.
16.观察下列各式:2x,﹣4x3,6x5,﹣8x7…,请根据你的发现的规律,写出第n个式子是 (﹣1)n+12nx2n﹣1 .
【分析】首先根据第1个、第2个、第3个、第4个单项式的系数分别是2=2×1、﹣4=﹣2×2、6=2×3、﹣8=﹣2×4,可得第n个单项式的系数是(﹣1)n+12n;然后根据第1个、第2个、第3个、第4个单项式的次数分别是1、3、5、7,可得第n个单项式的次数是2n﹣1,据此判断出第n个式子是多少即可.
【解答】解:∵2=2×1、﹣4=﹣2×2、6=2×3、﹣8=﹣2×4,
∴第n个单项式的系数(﹣1)n+12n;
∵第1个、第2个、第3个、第4个单项式的次数分别是1、3、5、7,
∴第n个单项式的次数是2n﹣1,
∴第n个式子是(﹣1)n+12nx2n﹣1.
故答案为:(﹣1)n+12nx2n﹣1.
【点评】此题主要考查了单项式问题,要熟练掌握,解答此题的关键是分别判断出第n个单项式的系数和次数各是多少.
17.多项式x+7是关于x的二次三项式,则m= 2 .
【分析】由于多项式是关于x的二次三项式,所以|m|=2,但﹣(m+2)≠0,根据以上两点可以确定m的值.
【解答】解:∵多项式是关于x的二次三项式,
∴|m|=2,
∴m=±2,
但﹣(m+2)≠0,
即m≠﹣2,
综上所述,m=2,故填空答案:2.
【点评】本题解答时容易忽略条件﹣(m+2)≠0,从而误解为m=±2.
18.有一个关于x的二次三项式,它的二次项系数为3,一次项系数和常数项都是﹣1,试写出这个多项式 3x2﹣x﹣1 .
【分析】由于多项式是由单项式组成的,而多项式的次数是“多项式中次数最高的项的次数”,而关于x的二次三项式,二次项系数是3,一次项系数和常数项是﹣1,根据前面的定义即可确定这个二次三项式.
【解答】解:∵关于x的二次三项式,二次项系数是3,
∴二次项是3x2,
又一次项系数和常数项是﹣1,
则一次项是﹣x,常数项为﹣1,
则这个二次三项式,3x2﹣x﹣1,
故填空答案:3x2﹣x﹣1.
【点评】本题考查多项式的知识,多项式是由单项式组成的,本题首先要确定是由几个单项式组成,要记住常数项也是一项,单项式前面的符号也应带着.
三.解答题(共8小题)
19.某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家6月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
【分析】(1)根据题意可得水费应分两部分:不超过10吨的部分的水费+超过10吨部分的水费,把两部分加起来即可;
(2)首先根据所交的水费讨论出用水是否超过了10吨,再根据水费计算出用水的吨数;
(3)此题要分两种情况进行讨论:①当0<a≤10时,②当a>10时,分别进行计算即可.
【解答】解:(1)10×2+(16﹣10)×2.5=35(元),
答:应交水费35元;
(2)设黄老师家6月份用水x吨,由题意得
10×2+2.5×(x﹣10)=30,
解得x=14,
答:黄老师家6月份用水14吨;
(3)①当0<a≤10时,应交水费为2a(元),
②当a>10时,应交水费为:20+2.5(a﹣10)=2.5a﹣5(元).
【点评】此题主要考查了由实际问题列代数式,关键是正确理解题意,分清楚如何计算水费.
20.当x=1,y=﹣6时,求下列代数式的值.
(1)x2+y2
(2)(x+y)2
(3)x2﹣2xy+y2.
【分析】把x=1,y=﹣6分别代入计算即可.
【解答】解:当x=1,y=﹣6时,
(1)x2+y2=12+(﹣6)2=1+36=37;
(2)(x+y)2=(1﹣6)2=(﹣5)2=25;
(3)x2﹣2xy+y2=12﹣2×1×(﹣6)+(﹣6)2=1+12+36=49.
【点评】本题主要考查代数式的求值,掌握代数式求值的方法即把所给字母的值代入计算是解题的关键.
21.阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛尝试应用
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是 ﹣(a﹣b)2 ;
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值 ﹣9 .
【分析】(1)把(a﹣b)2看成一个整体,运用合并同类项法则进行计算即可;
(2)把3x2﹣6y﹣21变形,得到3(x2﹣2y)﹣21,再根据整体代入法进行计算即可.
【解答】解:(1)把(a﹣b)2看成一个整体,则3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2=(3﹣6+2)(a﹣b)2=﹣(a﹣b)2;
(2)∵x2﹣2y=4,
∴原式=3(x2﹣2y)﹣21=12﹣21=﹣9.
故答案为:﹣(a﹣b)2;﹣9.
【点评】本题主要考查了整式的加减,解决问题的关键是运用整体思想;给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
22.先去括号、再合并同类项
①2(a﹣b+c)﹣3(a+b﹣c)
②3a2b﹣2[ab2﹣2(a2b﹣2ab2)].
【分析】根据括号前是正号,去掉括号及正号,括号里的各项都不变,括号前是负号,去掉括号及负号,括号里的各项都变号,可得答案.
【解答】解:(1)原式=2a﹣2b+2c﹣3a﹣3b+3c
=(2a﹣3a)+(﹣2b﹣3b)+(2c+3c)
=﹣a﹣5b+5c;
(2)原式=3a2b﹣2(ab2﹣2a2b+4ab2)
=3a2b﹣10ab2+4a2b
=7a2b﹣10ab2.
【点评】本题考查了去括号与添括号,括号前是正号,去掉括号及正号,括号里的各项都不变,括号前是负号,去掉括号及负号,括号里的各项都变号.
23.已知g(﹣1)=g(4)=0,g(﹣3)=,g(﹣2)=2,试求三次多项式g(x)的表达式.
【分析】可设三次多项式g(x)的表达式为g(x)=ax3+bx2+cx+d,根据待定系数法即可求解.
【解答】解:设g(x)=ax3+bx2+cx+d,
∵g(﹣1)=g(4)=0,g(﹣3)=,g(﹣2)=2,
∴,
解得.
故三次多项式g(x)的表达式为g(x)=x3﹣x2﹣x﹣.
【点评】考查了多项式,关键是熟练掌握待定系数法,以及解多元方程组,难度较大.
24.计算:
(1)3y2﹣2y+4y2
(2)st+4﹣3st﹣4;
(3)2(2ab+3a)﹣3(2a﹣ab);
(4)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.
(5)(﹣1)3﹣(1﹣)÷3×[3﹣(﹣3)2].
(6)7×1÷(﹣9+19);
(7)﹣24×(﹣+﹣);
(8)(﹣81)÷2+÷(﹣16);
【分析】(1)原式合并同类项即可得到结果;
(2)原式合并同类项即可得到结果;
(3)原式去括号合并即可得到结果;
(4)原式去括号合并即可得到结果;
(5)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(6)原式先计算括号里的运算,再算乘除法运算即可求出值;
(7)根据乘法分配律计算即可得到结果;
(8)先算除法,再算加减,即可得到结果.
【解答】解:(1)3y2﹣2y+4y2
=7y2﹣2y;
(2)st+4﹣3st﹣4;
=﹣st;
(3)2(2ab+3a)﹣3(2a﹣ab);
=4ab+6a﹣6a+3ab,
=7ab;
(4)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.
=a2﹣[﹣4ab+ab﹣a2]﹣2ab,
=a2+4ab﹣ab+a2﹣2ab,
=2a2+ab;
(5)(﹣1)3﹣(1﹣)÷3×[3﹣(﹣3)2].
=﹣1﹣××(3﹣9),
=﹣1﹣,
=﹣1+1,
=0;
(6)7×1÷(﹣9+19);
=×÷10,
=,
=;
(7)﹣24×(﹣+﹣);
=﹣24×﹣24×+24×,
=12﹣18+8,
=2;
(8)(﹣81)÷2+÷(﹣16);
=﹣81×+×,
=﹣36﹣,
=﹣36.
【点评】此题考查了整式的加减和有理数的混合运算,熟练掌握运算法则是解本题的关键.
25.如图,已知a、b、c在数轴上的位置,求|b+c|﹣|a﹣b|﹣|c﹣b|的值.
【分析】根据a、b、c在数轴上的位置,先进行绝对值的化简,然后合并.
【解答】解:由图可得,a<0<b<c,
则|b+c|﹣|a﹣b|﹣|c﹣b|
=b+c+a﹣b﹣c+b
=a+b.
【点评】本题考查了整式的加减,解答本题的关键是掌握绝对值的化简以及合并同类项法则.
26.计算
(1)3+(﹣)﹣()+2
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣)2
(3)(3a﹣2)+3(5﹣a)﹣13
(4)||+||+||+…+||
【分析】(1)将带分数化为整数和真分数的形式,将互为相反数相加为0,最后相加可得结果;
(2)先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
(3)先去括号,再合并同类项,可得结果;
(4)先将绝对值化去,并找规律,可得结果.
【解答】解:(1)3+(﹣)﹣()+2,
=3+﹣++2+,
=3+2+1,
=6;
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣)2,
=﹣64+3×4﹣6×9,
=﹣64+12﹣54,
=﹣118+12,
=﹣106;
(3)(3a﹣2)+3(5﹣a)﹣13,
=3a﹣2+15﹣3a﹣13,
=0;
(4)||+||+||+…+||,
=1﹣+﹣+﹣+…+﹣,
=1﹣,
=.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
一.选择题(共10小题)
1.若a是有理数,那么在①a+1,②|a+1|,③|a|+1,④a2+1中,一定是正数的有( )
A.1个 B.2个 C.3个 D.4个
2.为参加“爱我校园”摄影赛,小明同学将参与植树活动的照片放大为长acm,宽acm的形状,又精心在四周加上了宽2cm的木框,则这幅摄影作品占的面积是( )cm2.
A. a2﹣a+4 B. a2﹣7a+16 C. a2+a+4 D. a2+7a+16
3.如果2x﹣y=3,那么代数式4﹣2x+y的值为( )
A.﹣1 B.4 C.﹣4 D.1
4.下列运算正确的是( )
A.5xy﹣4xy=1 B.3x2+2x3=5x5
C.x2﹣x=x D.3x2+2x2=5x2
5.已知一列数,a1=,a2=,a3=,a4=…,当a0=3时,则a2018等于( )
A.3 B.﹣2 C. D.
6.若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有( )个.
A.5 B.4 C.3 D.2
7.有7个如图①的长为x,宽为y(x>y)的小长方形,按图②的方式不重叠的放在长方形ABCD中,未被覆盖的部分用阴影表示,若右下角阴影部分的面积S2与左上角阴影部分的面积S1之差为S,当BC的长度变化时,按照相同的放置方式,S始终保持不变,则x与y满足的关系式为( )
A.x=3y B.x=3y+1 C.x=2y D.x=2y+1
8.如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积S1与(2)图长方形的面积S2的比是多少?( )
A.2:3 B.1:2 C.3:4 D.1:1
9.已知a<b,那么a﹣b和它的相反数的差的绝对值是( )
A.b﹣a B.2b﹣2a C.﹣2a D.2b
10.已知a﹣b=3,c+d=2,则(a+c)﹣(b﹣d)的值为( )
A.1 B.﹣1 C.5 D.﹣5
二.填空题(共8小题)
11.如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为
12.当x=3时,代数式px3+qx+1的值为﹣2016,则当x=﹣3时,px3+qx+1的值是 .
13.若4x4yn+1与﹣5xmy2的和仍为单项式,则m﹣n= .
14.若﹣4xay+x2yb=﹣3x2y,则b﹣a= .
15.已知3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,则(﹣1)n+1= .
16.观察下列各式:2x,﹣4x3,6x5,﹣8x7…,请根据你的发现的规律,写出第n个式子是 .
17.多项式x+7是关于x的二次三项式,则m= .
18.有一个关于x的二次三项式,它的二次项系数为3,一次项系数和常数项都是﹣1,试写出这个多项式 .
三.解答题(共8小题)
19.某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家6月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
20.当x=1,y=﹣6时,求下列代数式的值.
(1)x2+y2
(2)(x+y)2
(3)x2﹣2xy+y2.
21.阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛尝试应用
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是 ;
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值 .
22.先去括号、再合并同类项
①2(a﹣b+c)﹣3(a+b﹣c)
②3a2b﹣2[ab2﹣2(a2b﹣2ab2)].
23.已知g(﹣1)=g(4)=0,g(﹣3)=,g(﹣2)=2,试求三次多项式g(x)的表达式.
24.计算:
(1)3y2﹣2y+4y2
(2)st+4﹣3st﹣4;
(3)2(2ab+3a)﹣3(2a﹣ab);
(4)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.
(5)(﹣1)3﹣(1﹣)÷3×[3﹣(﹣3)2].
(6)7×1÷(﹣9+19);
(7)﹣24×(﹣+﹣);
(8)(﹣81)÷2+÷(﹣16);
25.如图,已知a、b、c在数轴上的位置,求|b+c|﹣|a﹣b|﹣|c﹣b|的值.
26.计算
(1)3+(﹣)﹣()+2
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣)2
(3)(3a﹣2)+3(5﹣a)﹣13
(4)||+||+||+…+||
2020年北师大版七年级上册数学《第3章 整式及其加减》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.若a是有理数,那么在①a+1,②|a+1|,③|a|+1,④a2+1中,一定是正数的有( )
A.1个 B.2个 C.3个 D.4个
【分析】通过给a一数值,举反例,排除法求解.
【解答】解:①a=﹣2时,a+1=﹣1是负数;②a=﹣1时,|a+1|=0不是正数;不论a取何值,都有|a|+1≥1、a2+1≥1;
所以一定是正数的有③|a|+1,④a2+1;故选B.
【点评】本题考查知识点为:一个数的绝对值和一个数的平方一定是非负数,所以加上一个正数后则一定是正数.
2.为参加“爱我校园”摄影赛,小明同学将参与植树活动的照片放大为长acm,宽acm的形状,又精心在四周加上了宽2cm的木框,则这幅摄影作品占的面积是( )cm2.
A. a2﹣a+4 B. a2﹣7a+16 C. a2+a+4 D. a2+7a+16
【分析】此题涉及面积公式的运用,解答时直接运用面积的公式求出答案.
【解答】解:根据题意可知,
这幅摄影作品占的面积是a2+4(a+4)+4(a+4)﹣4×4=a2+7a+16.
故选:D.
【点评】列代数式的关键是正确理解文字语言中的关键词,找到其中的数量关系列出式子.
3.如果2x﹣y=3,那么代数式4﹣2x+y的值为( )
A.﹣1 B.4 C.﹣4 D.1
【分析】将2x﹣y的值整体代入到4﹣2x+y=4﹣(2x﹣y)即可.
【解答】解:当2x﹣y=3时,
4﹣2x+y=4﹣(2x﹣y)=4﹣3=1,
故选:D.
【点评】本题主要考查代数式的求值,运用整体代入思想是解题的关键.
4.下列运算正确的是( )
A.5xy﹣4xy=1 B.3x2+2x3=5x5
C.x2﹣x=x D.3x2+2x2=5x2
【分析】区分是否是同类项,在根据合并同类项的法则合并即可.
【解答】解:A、5xy﹣4xy=xy,故本选项错误;
B、不是同类项,不能合并,故本选项错误;
C、不是同类项,不能合并,故本选项错误;
D、3x2+2x2=5x2,故本选项正确;
故选:D.
【点评】本题考查了同类项和合并同类项等知识点的应用,同类项是指所含字母相同,并且相同字母的指数分别相等的项;同类项的系数相加,字母和字母的指数不变.
5.已知一列数,a1=,a2=,a3=,a4=…,当a0=3时,则a2018等于( )
A.3 B.﹣2 C. D.
【分析】根据数字的变化类寻找规律即可求解.
【解答】解:当a0=3时,
a1=﹣2,a2=,a3=,a4=3,
a5=﹣2,a6=…
∵2018÷4=504…2
∴a2018=.
故选:C.
【点评】本题考查了数字的变化类,解决本题的关键是通过计算寻找规律.
6.若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有( )个.
A.5 B.4 C.3 D.2
【分析】多项式相减,也就是合并同类项,合并同类项时只是把系数相加减,字母和字母的指数不变,所以结果的次数一定不高于2次,由此可以判定正确个数.
【解答】解:∵多项式相减,也就是合并同类项,
而合并同类项时只是把系数相加减,字母和字母的指数不变,
∴结果的次数一定不高于2次,
当二次项的系数相同时,合并后结果为0,
所以(1)和(2)(5)是错误的.
故选:C.
【点评】此题要准确把握合并同类项的法则,合并同类项时只是把系数相加减,字母和字母的指数不变,当二次项的系数互为相反数时,合并后结果为0.
7.有7个如图①的长为x,宽为y(x>y)的小长方形,按图②的方式不重叠的放在长方形ABCD中,未被覆盖的部分用阴影表示,若右下角阴影部分的面积S2与左上角阴影部分的面积S1之差为S,当BC的长度变化时,按照相同的放置方式,S始终保持不变,则x与y满足的关系式为( )
A.x=3y B.x=3y+1 C.x=2y D.x=2y+1
【分析】表示出左上角与右下角部分的面积,求出之差,根据差与BC无关,即与PC无关,即可求出x与y的关系式.
【解答】解:左上角阴影部分的长为AE=BP+PC﹣ED=x+PC﹣3y﹣x=PC﹣3y,宽为AF=x,右下角阴影部分的长为PC,宽CG=x+y,
∴阴影部分面积之差S=AE?AF﹣xy﹣PC?BF﹣x(x+y﹣2y)=x(PC﹣3y)﹣xy﹣PC?2y﹣x(x﹣y)=PC(x﹣2y)﹣3xy﹣x2,
则x﹣2y=0,即x=2y.
故选:C.
【点评】此题考查了整式的混合运算的应用,弄清题意是解本题的关键.
8.如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积S1与(2)图长方形的面积S2的比是多少?( )
A.2:3 B.1:2 C.3:4 D.1:1
【分析】本题需先设图(1)中长方形的长为acm,宽为bcm,图(2)中长方形的宽为xcm,长为ycm,再结合图形分别得出图形(3)的阴影周长和图形(4)的阴影周长,相等后列等式可得:a=2y,x=3b,最后根据长方形面积公式可得结论.
【解答】解:设图(1)中长方形的长为acm,宽为bcm,图(2)中长方形的宽为xcm,长为ycm,
由两个长方形ABCD的AD=3b+2y=a+x,
∴图(3)阴影部分周长为:2(3b+2y+DC﹣x)=6b+4y+2DC﹣2x=2a+2x+2DC﹣2x=2a+2DC,
∴图(4)阴影部分周长为:2(a+x+DC﹣3b)=2a+2x+2DC﹣6b=2a+2x+2DC﹣2(a+x﹣2y)=2DC+4y,
∵两种方式未覆盖的部分(阴影部分)的周长一样,
∴2a+2DC=2DC+4y,
a=2y,
∵3b+2y=a+x,
∴x=3b,
∴===,
故选:A.
【点评】本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
9.已知a<b,那么a﹣b和它的相反数的差的绝对值是( )
A.b﹣a B.2b﹣2a C.﹣2a D.2b
【分析】a﹣b的相反数是b﹣a,可得a﹣b和它的相反数为:(a﹣b)﹣(b﹣a)=2a﹣2b,又因为a<b,可知2a﹣2b<0,所以|(a﹣b)﹣(b﹣a)|=2b﹣2a.
【解答】解:依题意可得:|(a﹣b)﹣(b﹣a)|=2b﹣2a.故选B.
【点评】此题考查的是相反数的概念和整式的加减运算和绝对值的意义.
10.已知a﹣b=3,c+d=2,则(a+c)﹣(b﹣d)的值为( )
A.1 B.﹣1 C.5 D.﹣5
【分析】原式去括号整理后,将已知等式代入计算即可求出值.
【解答】解:∵a﹣b=3,c+d=2,
∴原式=a+c﹣b+d=(a﹣b)+(c+d)=3+2=5.
故选:C.
【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.
二.填空题(共8小题)
11.如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为 a2﹣3a+18.
【分析】根据面积的和差:两个正方形的面积和减去两个三角形的面积,可得答案.
【解答】解:阴影部分的面积
=a2+62﹣a2﹣(a+6)×6
=a2+36﹣a2﹣3a﹣18
=a2﹣3a+18,
故答案为: a2﹣3a+18.
【点评】本题考查了代数式求值,利用面积的和差得出关系式是解题关键.
12.当x=3时,代数式px3+qx+1的值为﹣2016,则当x=﹣3时,px3+qx+1的值是 2018 .
【分析】把x=3代入代数式,依据其值为2016,得到27p+3q的值,再将x=﹣3及27p+3q的值代入原式计算即可.
【解答】解:把x=3代入px3+qx+1,得:27p+3q=﹣2017,
则当x=﹣3时,原式=﹣27p﹣3q+1=2017+1=2018,
故答案为:2018.
【点评】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.
13.若4x4yn+1与﹣5xmy2的和仍为单项式,则m﹣n= 3 .
【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出n,m的值,再代入代数式计算即可.
【解答】解:根据题意得:m=4,n+1=2,
解得:n=1,
则m﹣n=4﹣1=3.
故答案是:3.
【点评】本题考查了同类项的定义,同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.
14.若﹣4xay+x2yb=﹣3x2y,则b﹣a= ﹣1 .
【分析】依据﹣4xay+x2yb=﹣3x2y,即可得到﹣4xay与x2yb是同类项,进而得出a,b的值.
【解答】解:∵﹣4xay+x2yb=﹣3x2y,
∴﹣4xay与x2yb是同类项,
∴,
∴b﹣a=1﹣2=﹣1,
故答案为:﹣1.
【点评】本题主要考查了同类项的定义,要掌握同类项的概念,会辨别同类项,并准确地掌握判断同类项的两条标准:带有相同系数的代数项;字母和字母指数.
15.已知3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,则(﹣1)n+1= 1 .
【分析】多项式的前两项次数分别为2、4,第三项次数为n﹣1+2,而后面单项式次数为8,故只有n﹣1+2=8.列方程可解本题.
【解答】解:∵3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,
∴n﹣1+2=8,即n+1=8.
∴(﹣1)n+1=1.
【点评】多项式里次数最高项的次数叫做这个多项式的次数.单项式中,所有字母的指数和叫做这个单项式的次数.注意π是数字因数.
16.观察下列各式:2x,﹣4x3,6x5,﹣8x7…,请根据你的发现的规律,写出第n个式子是 (﹣1)n+12nx2n﹣1 .
【分析】首先根据第1个、第2个、第3个、第4个单项式的系数分别是2=2×1、﹣4=﹣2×2、6=2×3、﹣8=﹣2×4,可得第n个单项式的系数是(﹣1)n+12n;然后根据第1个、第2个、第3个、第4个单项式的次数分别是1、3、5、7,可得第n个单项式的次数是2n﹣1,据此判断出第n个式子是多少即可.
【解答】解:∵2=2×1、﹣4=﹣2×2、6=2×3、﹣8=﹣2×4,
∴第n个单项式的系数(﹣1)n+12n;
∵第1个、第2个、第3个、第4个单项式的次数分别是1、3、5、7,
∴第n个单项式的次数是2n﹣1,
∴第n个式子是(﹣1)n+12nx2n﹣1.
故答案为:(﹣1)n+12nx2n﹣1.
【点评】此题主要考查了单项式问题,要熟练掌握,解答此题的关键是分别判断出第n个单项式的系数和次数各是多少.
17.多项式x+7是关于x的二次三项式,则m= 2 .
【分析】由于多项式是关于x的二次三项式,所以|m|=2,但﹣(m+2)≠0,根据以上两点可以确定m的值.
【解答】解:∵多项式是关于x的二次三项式,
∴|m|=2,
∴m=±2,
但﹣(m+2)≠0,
即m≠﹣2,
综上所述,m=2,故填空答案:2.
【点评】本题解答时容易忽略条件﹣(m+2)≠0,从而误解为m=±2.
18.有一个关于x的二次三项式,它的二次项系数为3,一次项系数和常数项都是﹣1,试写出这个多项式 3x2﹣x﹣1 .
【分析】由于多项式是由单项式组成的,而多项式的次数是“多项式中次数最高的项的次数”,而关于x的二次三项式,二次项系数是3,一次项系数和常数项是﹣1,根据前面的定义即可确定这个二次三项式.
【解答】解:∵关于x的二次三项式,二次项系数是3,
∴二次项是3x2,
又一次项系数和常数项是﹣1,
则一次项是﹣x,常数项为﹣1,
则这个二次三项式,3x2﹣x﹣1,
故填空答案:3x2﹣x﹣1.
【点评】本题考查多项式的知识,多项式是由单项式组成的,本题首先要确定是由几个单项式组成,要记住常数项也是一项,单项式前面的符号也应带着.
三.解答题(共8小题)
19.某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家6月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
【分析】(1)根据题意可得水费应分两部分:不超过10吨的部分的水费+超过10吨部分的水费,把两部分加起来即可;
(2)首先根据所交的水费讨论出用水是否超过了10吨,再根据水费计算出用水的吨数;
(3)此题要分两种情况进行讨论:①当0<a≤10时,②当a>10时,分别进行计算即可.
【解答】解:(1)10×2+(16﹣10)×2.5=35(元),
答:应交水费35元;
(2)设黄老师家6月份用水x吨,由题意得
10×2+2.5×(x﹣10)=30,
解得x=14,
答:黄老师家6月份用水14吨;
(3)①当0<a≤10时,应交水费为2a(元),
②当a>10时,应交水费为:20+2.5(a﹣10)=2.5a﹣5(元).
【点评】此题主要考查了由实际问题列代数式,关键是正确理解题意,分清楚如何计算水费.
20.当x=1,y=﹣6时,求下列代数式的值.
(1)x2+y2
(2)(x+y)2
(3)x2﹣2xy+y2.
【分析】把x=1,y=﹣6分别代入计算即可.
【解答】解:当x=1,y=﹣6时,
(1)x2+y2=12+(﹣6)2=1+36=37;
(2)(x+y)2=(1﹣6)2=(﹣5)2=25;
(3)x2﹣2xy+y2=12﹣2×1×(﹣6)+(﹣6)2=1+12+36=49.
【点评】本题主要考查代数式的求值,掌握代数式求值的方法即把所给字母的值代入计算是解题的关键.
21.阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛尝试应用
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是 ﹣(a﹣b)2 ;
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值 ﹣9 .
【分析】(1)把(a﹣b)2看成一个整体,运用合并同类项法则进行计算即可;
(2)把3x2﹣6y﹣21变形,得到3(x2﹣2y)﹣21,再根据整体代入法进行计算即可.
【解答】解:(1)把(a﹣b)2看成一个整体,则3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2=(3﹣6+2)(a﹣b)2=﹣(a﹣b)2;
(2)∵x2﹣2y=4,
∴原式=3(x2﹣2y)﹣21=12﹣21=﹣9.
故答案为:﹣(a﹣b)2;﹣9.
【点评】本题主要考查了整式的加减,解决问题的关键是运用整体思想;给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
22.先去括号、再合并同类项
①2(a﹣b+c)﹣3(a+b﹣c)
②3a2b﹣2[ab2﹣2(a2b﹣2ab2)].
【分析】根据括号前是正号,去掉括号及正号,括号里的各项都不变,括号前是负号,去掉括号及负号,括号里的各项都变号,可得答案.
【解答】解:(1)原式=2a﹣2b+2c﹣3a﹣3b+3c
=(2a﹣3a)+(﹣2b﹣3b)+(2c+3c)
=﹣a﹣5b+5c;
(2)原式=3a2b﹣2(ab2﹣2a2b+4ab2)
=3a2b﹣10ab2+4a2b
=7a2b﹣10ab2.
【点评】本题考查了去括号与添括号,括号前是正号,去掉括号及正号,括号里的各项都不变,括号前是负号,去掉括号及负号,括号里的各项都变号.
23.已知g(﹣1)=g(4)=0,g(﹣3)=,g(﹣2)=2,试求三次多项式g(x)的表达式.
【分析】可设三次多项式g(x)的表达式为g(x)=ax3+bx2+cx+d,根据待定系数法即可求解.
【解答】解:设g(x)=ax3+bx2+cx+d,
∵g(﹣1)=g(4)=0,g(﹣3)=,g(﹣2)=2,
∴,
解得.
故三次多项式g(x)的表达式为g(x)=x3﹣x2﹣x﹣.
【点评】考查了多项式,关键是熟练掌握待定系数法,以及解多元方程组,难度较大.
24.计算:
(1)3y2﹣2y+4y2
(2)st+4﹣3st﹣4;
(3)2(2ab+3a)﹣3(2a﹣ab);
(4)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.
(5)(﹣1)3﹣(1﹣)÷3×[3﹣(﹣3)2].
(6)7×1÷(﹣9+19);
(7)﹣24×(﹣+﹣);
(8)(﹣81)÷2+÷(﹣16);
【分析】(1)原式合并同类项即可得到结果;
(2)原式合并同类项即可得到结果;
(3)原式去括号合并即可得到结果;
(4)原式去括号合并即可得到结果;
(5)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(6)原式先计算括号里的运算,再算乘除法运算即可求出值;
(7)根据乘法分配律计算即可得到结果;
(8)先算除法,再算加减,即可得到结果.
【解答】解:(1)3y2﹣2y+4y2
=7y2﹣2y;
(2)st+4﹣3st﹣4;
=﹣st;
(3)2(2ab+3a)﹣3(2a﹣ab);
=4ab+6a﹣6a+3ab,
=7ab;
(4)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.
=a2﹣[﹣4ab+ab﹣a2]﹣2ab,
=a2+4ab﹣ab+a2﹣2ab,
=2a2+ab;
(5)(﹣1)3﹣(1﹣)÷3×[3﹣(﹣3)2].
=﹣1﹣××(3﹣9),
=﹣1﹣,
=﹣1+1,
=0;
(6)7×1÷(﹣9+19);
=×÷10,
=,
=;
(7)﹣24×(﹣+﹣);
=﹣24×﹣24×+24×,
=12﹣18+8,
=2;
(8)(﹣81)÷2+÷(﹣16);
=﹣81×+×,
=﹣36﹣,
=﹣36.
【点评】此题考查了整式的加减和有理数的混合运算,熟练掌握运算法则是解本题的关键.
25.如图,已知a、b、c在数轴上的位置,求|b+c|﹣|a﹣b|﹣|c﹣b|的值.
【分析】根据a、b、c在数轴上的位置,先进行绝对值的化简,然后合并.
【解答】解:由图可得,a<0<b<c,
则|b+c|﹣|a﹣b|﹣|c﹣b|
=b+c+a﹣b﹣c+b
=a+b.
【点评】本题考查了整式的加减,解答本题的关键是掌握绝对值的化简以及合并同类项法则.
26.计算
(1)3+(﹣)﹣()+2
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣)2
(3)(3a﹣2)+3(5﹣a)﹣13
(4)||+||+||+…+||
【分析】(1)将带分数化为整数和真分数的形式,将互为相反数相加为0,最后相加可得结果;
(2)先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
(3)先去括号,再合并同类项,可得结果;
(4)先将绝对值化去,并找规律,可得结果.
【解答】解:(1)3+(﹣)﹣()+2,
=3+﹣++2+,
=3+2+1,
=6;
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣)2,
=﹣64+3×4﹣6×9,
=﹣64+12﹣54,
=﹣118+12,
=﹣106;
(3)(3a﹣2)+3(5﹣a)﹣13,
=3a﹣2+15﹣3a﹣13,
=0;
(4)||+||+||+…+||,
=1﹣+﹣+﹣+…+﹣,
=1﹣,
=.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
