2020年北师大版七年级上册数学《第6章 数据的收集与整理》单元测试卷(解析版)
文档属性
| 名称 | 2020年北师大版七年级上册数学《第6章 数据的收集与整理》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 14:06:32 | ||
图片预览



文档简介
2020年北师大版七年级上册数学《第6章 数据的收集与整理》单元测试卷
一.选择题(共9小题)
1.为了考查一批日光灯管的使用寿命,从中抽取了30只进行试验,在这个问题中,下列说法正确的有( )
①总体是指这批日光灯管的全体;
②个体是指每只日光灯管的使用寿命;
③样本是指从中抽取的30只日光灯管的使用寿命;
④样本容量是30只.
A.1个 B.2个 C.3个 D.4个
2.下列调查,样本具有代表性的是( )
A.了解全校同学对课程的喜欢情况,对某班男同学进行调查
B.了解某小区居民的防火意识,对你们班同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查
3.青青的袋中有红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则青青的袋中大约有黄球( )
A.5个 B.10个 C.15个 D.30个
4.下表为某公司200名职员年龄的人数分配表,其中36~42岁及50~56岁的人数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄 22~28 29~35 36~42 43~49 50~56 57~63
次数 6 40 42 2
A.10 B.45 C.55 D.99
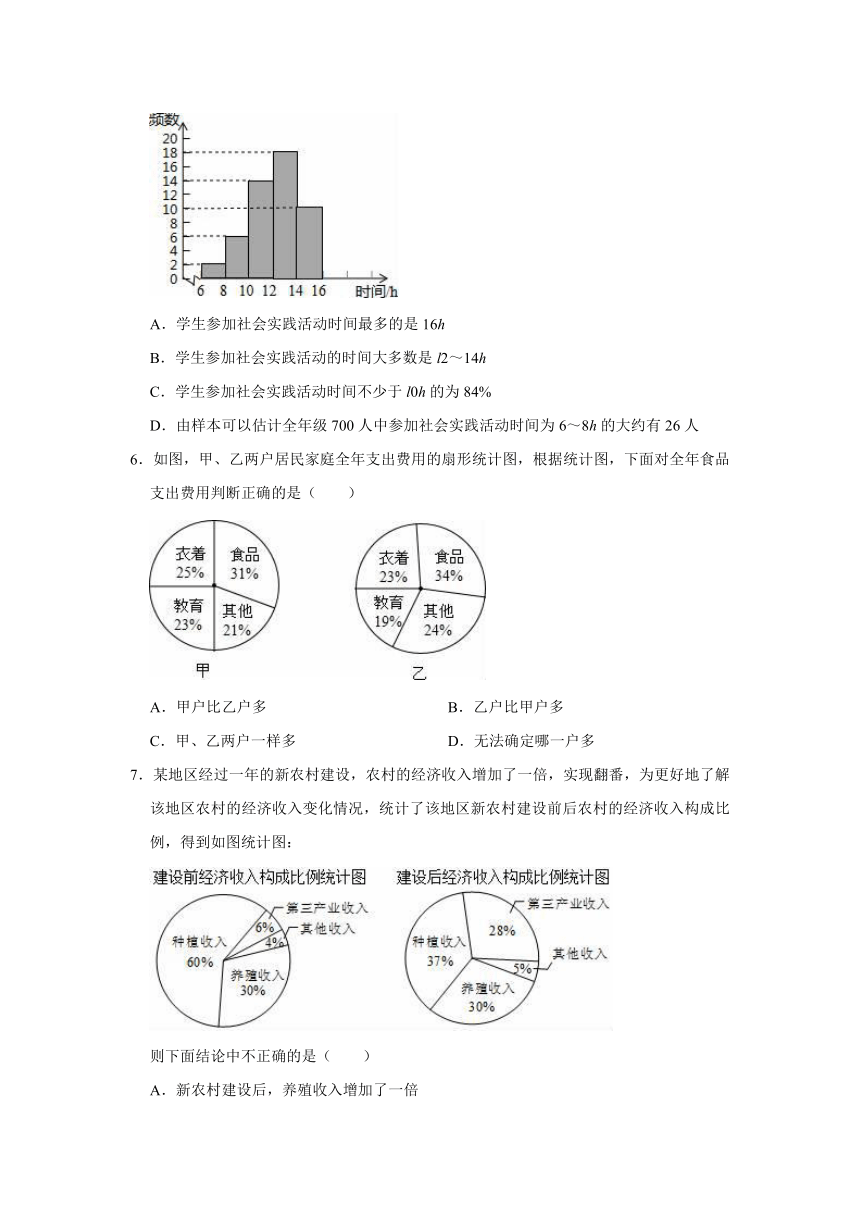
5.为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
A.学生参加社会实践活动时间最多的是16h
B.学生参加社会实践活动的时间大多数是l2~14h
C.学生参加社会实践活动时间不少于l0h的为84%
D.由样本可以估计全年级700人中参加社会实践活动时间为6~8h的大约有26人
6.如图,甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如图统计图:
则下面结论中不正确的是( )
A.新农村建设后,养殖收入增加了一倍
B.新农村建设后,种植收入减少
C.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
D.新农村建设后,其他收入增加了一倍以上
8.某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知乙类书有90本,则丙类书的本数是( )
A.80 B.144 C.200 D.90
9.小张一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小张一星期的鸡蛋开支占总开支的百分比为( )
A.3% B.10% C.30 D.不能确定
二.填空题(共7小题)
10.近几年,人们的环保意识逐渐增加,“白色污染”现象越来越受到人们的重视.小颖同学想了解班上同学家里在一年内丢弃废塑料袋的个数,你认为采用 方式合适一些.
11.小颖为了解家里的用电量,在5月初连续8天同一时刻观察家里的电表显示的数字,记录如下,估计小颖家5月份的总用电量是 千瓦时.
日期(号) 1 2 3 4 5 6 7 8
电表显示的数字(千瓦时) 117 120 124 129 135 138 142 145
12.有50个数据,把它们分成五组,第一、二、三、四、五组的数据个数分别是3,7,14、x、6,则第四组的频率为 .
13.为了了解某中学初三年级250名学生升学考试的数学成绩,从中抽取了50名学生的数学成绩进行分析,求得样本=93.5.下面是50名学生数学成绩的频率分布表:
分组 频数累计 频数 频率
60.5~70.5 正 3 a
70.5~80.5 正正 6 0.12
80.5~90.5 正正 9 0.18
90.5~100.5 正正正正 17 0.34
100.5~110.5 正正 b 0.2
110.5~120.5 正 5 0.1
合计 50 1
根据题中给出的条件回答下列问题:
(1)在这次抽样分析的过程中,样本是 ;
(2)频率分布表中的数据a= b= ;
(3)估计该校初三年级这次升学考试的数学平均成绩约为 分;
(4)在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为 人.
14.将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,则该班共有 人.
15.下表是某校初一(7)班20名学生某次数学成绩的统计表:若这20名学生平均成绩为a(a是整数),则a至少是 分.
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
16.某校图书管理员清理阅览室的课外书籍时,将其中甲、乙,丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有45本,则丙类书有 本.
三.解答题(共8小题)
17.阅读对人成长的影响是很大的.希望中学为了了解学生课外阅读的情况,就“你最喜欢的图书类别”(只选一项)随机调查了部分学生,并将调查结果统计后绘制成如下统计表和条形统计图.
种类 频数 频率
科普 0.15
艺术 78
文学 0.59
其它 81
请你根据统计图表提供的信息解答下列问题:
(1)这次随机调查了 名学生;
(2)把统计表和条形统计图补充完整;
(3)为满足同学们阅读兴趣,学校图书馆准备购进新书2000册.根据调查的数据,你对购进各类书籍的数量有何建议?
18.某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.
19.2012年5月13日为母亲节,某校结合学生实际,开展了形式多样的感恩教育活动.下面图1,图2分别是该校调查部分学生是否知道母亲生日情况的扇形统计图和频数分布直方图.
根据上图信息,解答下列问题:
(1)被调查的学生中,记不清母亲生日情况的学生有 人;
(2)本次被调查的学生总人数有 ,并补全频数分布直方图2;
(3)若这所学校共有学生2400人,已知被调查的学生中,知道母亲生日的女生人数是男生人数的2倍,请你通过计算估计该校知道母亲生日的女生和男生分别有多少人?
20.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
类别 A B C D
时间t(h) t<1 1≤t<2 2≤t<3 t≥3
人数 5a 5b 5c 5d
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
21.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
组别 分数段(x) 频数
A 0≤x<60 2
B 60≤x<70 5
C 70≤x<80 17
D 80≤x<90 a
E 90≤x≤100 b
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为 ,频数分布表中a的值为 ;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
22.某中学七年级开设了艺术课程,每名学生从合唱、管弦乐、舞蹈、动漫、吉他这五门课程中选择一门进行学习.为了解学生的选择意向,从七年级随机抽取了若干名同学进行了调查,将调查得到的结果绘制成如图所示的两幅统计图(均不完整).
根据题中信息,回答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)若该校七年级一共有240名学生,请估计其中有多少人会选择合唱课程.
23.“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?
24.在结束了380课时初中阶段教学内容的教学后,唐老师计划再增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1~图2),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2中的a= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“图形与几何”内容?
2020年北师大版七年级上册数学《第6章 数据的收集与整理》单元测试卷
参考答案与试题解析
一.选择题(共9小题)
1.为了考查一批日光灯管的使用寿命,从中抽取了30只进行试验,在这个问题中,下列说法正确的有( )
①总体是指这批日光灯管的全体;
②个体是指每只日光灯管的使用寿命;
③样本是指从中抽取的30只日光灯管的使用寿命;
④样本容量是30只.
A.1个 B.2个 C.3个 D.4个
【分析】本题考查的是确定总体.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”.我们在区分总体、个体、样本、样本容量这四个概念时,首先找出考查的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:本题中的总体是指这批日光灯管的全体的使用寿命,样本容量是30,所以①④不正确.
个体是指每只日光灯管的使用寿命,样本是指从中抽取的30只日光灯管的使用寿命,所以②和③正确.故选:B.
【点评】本题考查的是确定总体、个体、样本.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”
2.下列调查,样本具有代表性的是( )
A.了解全校同学对课程的喜欢情况,对某班男同学进行调查
B.了解某小区居民的防火意识,对你们班同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【解答】解:A、了解全校同学对课程的喜欢情况,对某班男同学进行调查,不具代表性、广泛性,故A错误;
B、了解某小区居民的防火意识,对你们班同学进行调查,调查不具代表性、广泛性,故B错误;
C、了解商场的平均日营业额,选在周末进行调查,调查不具有代表性、广泛性,故C错误;
D、了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查,调查具有代表性、广泛性,故D正确.
故选:D.
【点评】样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
3.青青的袋中有红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则青青的袋中大约有黄球( )
A.5个 B.10个 C.15个 D.30个
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手求解.
【解答】解:晓晓放入5个黑球后,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,故发现摸到黑球的频率为5%,
则可以由此估计袋中共有球=100(个),
说明此时袋中可能有100个球(包括5个黑球),故黄球有100×15%=15(个),
故选:C.
【点评】此题主要考查了利用频率估计概率,解答此题关键是要先计算出口袋中黑球的比例再算其个数.部分的具体数目=总体数目×相应频率.
4.下表为某公司200名职员年龄的人数分配表,其中36~42岁及50~56岁的人数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄 22~28 29~35 36~42 43~49 50~56 57~63
次数 6 40 42 2
A.10 B.45 C.55 D.99
【分析】根据图表求出36~42岁及50~56岁的职员人数,然后求出相对次数比,然后根据百分数的意义,扩大100倍即可得解.
【解答】解:由表知36~42岁及50~56岁的职员人数共有,
200﹣6﹣40﹣42﹣2=110人,
所以,a%+b%=×100%=55%,
所以a+b=55.
故选:C.
【点评】本题考查了频数分布表,本题难点在于a、b的和不是职员人数,而是相对次数比,这也是本题容易出错的地方.
5.为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
A.学生参加社会实践活动时间最多的是16h
B.学生参加社会实践活动的时间大多数是l2~14h
C.学生参加社会实践活动时间不少于l0h的为84%
D.由样本可以估计全年级700人中参加社会实践活动时间为6~8h的大约有26人
【分析】阅读频数分布直方图,根据直方图中获取的信息进行判断即可.
【解答】解:A、最后一个小组的时间范围为14~16h,但不代表一定有活动时间为16h的同学,故A错误;
B、18÷50=36%<50%,故B错误;
C、(14+18+10)÷50=84%,故C正确.
D、700×=28,故D错误.
故选:C.
【点评】本题主要考查的是频数分布直方图的认识,能够从直方图中获取有效信息是解题的关键.
6.如图,甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
【分析】甲户食品支出所占的百分率是把甲全年支出看作单位“1”,同理,乙户食品支出所占的百分率是把乙全年支出看作单位“1”,由于甲、乙两家全年支出无法确定,因此,两家食品支出的多少也无法确定.
【解答】解:∵甲、乙两户全年支出总数无法确定,
∴两户食品支出的多少也无法确定.
故选:D.
【点评】本题主要考查的是如何从扇形统计图获取信息.利用圆和扇形来表示总体和部分的关系,用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图.因此,从扇形图上只能看出各部分数量和总数量之间的关系.
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如图统计图:
则下面结论中不正确的是( )
A.新农村建设后,养殖收入增加了一倍
B.新农村建设后,种植收入减少
C.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
D.新农村建设后,其他收入增加了一倍以上
【分析】设建设前经济收入为a,建设后经济收入为2a.通过选项逐一分析新农村建设前后,经济收入情况,利用数据推出结果.
【解答】解:设建设前经济收入为a,建设后经济收入为2a.
A、建设后,养殖收入为30%×2a=60%a,
建设前,养殖收入为30%a,
故60%a÷30%a=2,故A项正确.
B、种植收入37%×2a﹣60%a=14%a>0,
故建设后,种植收入增加,故B项错误.
C、建设后,养殖收入与第三产业收入总和为(30%+28%)×2a=58%×2a,
经济收入为2a,
故(58%×2a)÷2a=58%>50%,故C项正确.
D、建设后,其他收入为5%×2a=10%a,
建设前,其他收入为4%a,
故10%a÷4%a=2.5>2,故D项正确.
故选:B.
【点评】本题主要考查扇形统计图的应用,命题的真假的判断,考查发现问题解决问题的能力.
8.某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知乙类书有90本,则丙类书的本数是( )
A.80 B.144 C.200 D.90
【分析】根据乙类书籍有90本,占总数的45%即可求得总书籍数,丙类所占的比例是1﹣15%﹣45%,所占的比例乘以总数即可求得丙类书的本数.
【解答】解:总数是:90÷45%=200(本),
丙类书的本数是:200×(1﹣15%﹣45%)=200×40%=80(本)
故选:A.
【点评】本题考查了扇形统计图,从扇形图上可以清楚地看出各部分数量和总数量之间的关系,正确求得总书籍数是关键.
9.小张一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小张一星期的鸡蛋开支占总开支的百分比为( )
A.3% B.10% C.30 D.不能确定
【分析】计算鸡蛋占食品开支的百分比,利用一星期的食品开支占总开支的百分比,即可求得一星期的鸡蛋开支占总开支的百分比.
【解答】解:根据一星期的食品开支图,可知鸡蛋占食品开支的百分比为:
×100%=10%,
∵一星期的食品开支占总开支的百分比为30%,
∴一星期的鸡蛋开支占总开支的百分比为30%×10%=3%.
故选:A.
【点评】本题主要考查了条形统计图以及扇形统计图的运用,通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
二.填空题(共7小题)
10.近几年,人们的环保意识逐渐增加,“白色污染”现象越来越受到人们的重视.小颖同学想了解班上同学家里在一年内丢弃废塑料袋的个数,你认为采用 抽样调查 方式合适一些.
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.了解班上同学家里在一年内丢弃废塑料袋的个数,考查的对象很多以及考查经费和时间都非常有限,普查就受到限制,这时就应选择抽样调查.
【解答】解:了解班上同学家里在一年内丢弃废塑料袋的个数,考查的对象很多以及考查经费和时间都非常有限,普查就受到限制,这时就应选择抽样调查.故填抽样.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
11.小颖为了解家里的用电量,在5月初连续8天同一时刻观察家里的电表显示的数字,记录如下,估计小颖家5月份的总用电量是 124 千瓦时.
日期(号) 1 2 3 4 5 6 7 8
电表显示的数字(千瓦时) 117 120 124 129 135 138 142 145
【分析】根据样本估计总体的统计思想:可先求出7天中用电量的平均数,作为5月份用电量的平均数,则一个月的用电总量即可求得.
【解答】解:31×=124(千瓦时).
【点评】统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体.
12.有50个数据,把它们分成五组,第一、二、三、四、五组的数据个数分别是3,7,14、x、6,则第四组的频率为 0.4 .
【分析】根据各小组频数之和等于数据总和,即可求得第四组的频数;再根据频率=频数÷总数,进行计算.
【解答】解:根据题意,得
第四组数据的个数x=50﹣(3+7+14+6)=20,
故第四组的频率为20÷50=0.4.
故答案为:0.4.
【点评】本题是对频率、频数灵活运用的综合考查.注意:各小组频数之和等于数据总和,各小组频率之和等于1.
13.为了了解某中学初三年级250名学生升学考试的数学成绩,从中抽取了50名学生的数学成绩进行分析,求得样本=93.5.下面是50名学生数学成绩的频率分布表:
分组 频数累计 频数 频率
60.5~70.5 正 3 a
70.5~80.5 正正 6 0.12
80.5~90.5 正正 9 0.18
90.5~100.5 正正正正 17 0.34
100.5~110.5 正正 b 0.2
110.5~120.5 正 5 0.1
合计 50 1
根据题中给出的条件回答下列问题:
(1)在这次抽样分析的过程中,样本是 50名学生的数学成绩 ;
(2)频率分布表中的数据a= 0.06 b= 10 ;
(3)估计该校初三年级这次升学考试的数学平均成绩约为 93.5 分;
(4)在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为 85 人.
【分析】(1)由于样本是总体中所抽取的一部分个体,根据已知条件即可确定题目中的样本;
(2)由于已知总人数为50,分别利用表格已知数据即可求解;
(3)利用样本估计总体的思想就可以解决问题;
(4)首先根据表格信息可以确定数学成绩在90.5~100.5的频率,然后利用样本估计总体的思想即可解决问题.
【解答】解:(1)在这次抽样分析的过程中,样本是50名学生的数学成绩;
(2)依题意得
a=3÷50=0.06,
b=0.2×50=10;
(3)∵所抽取了50名学生的数学成绩的样本=93.5
∴估计该校初三年级这次升学考试的数学平均成绩约为93.5分;
(4)依题意得初三年级数学成绩在90.5~100.5范围内的频率为0.34,
∴在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为0.34×250=85人.
【点评】此题既考查了样本估计总体的思想,也考查了正确利用频率分布表的能力,解题时首先根据表格信息可以分别确定a,b的值,然后利用样本估计总体的思想就可以解决问题.
14.将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,则该班共有 60 人.
【分析】依据各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,可得各组人数,进而得出总人数.
【解答】解:∵各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,
∴各组人数分别为5人、10人、25人、15人、5人,
∴总人数为:5+10+25+15+5=60(人),
故答案为:60.
【点评】本题主要考查了频数分布直方图,解题时注意:频数分布直方图中的小长方形高的比就是各组的频数之比.
15.下表是某校初一(7)班20名学生某次数学成绩的统计表:若这20名学生平均成绩为a(a是整数),则a至少是 79 分.
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
【分析】依据20名学生的总成绩为20a分列方程组,即可得到关系式a=84.5﹣x,再根据x的取值范围,即可得到a的最小取值.
【解答】解:由题可得,,
整理,得
a=84.5﹣x,
又∵x<12,且x为整数,
∴当x=11时,a的最小值为79,
故答案为:79.
【点评】本题主要考查了统计表的应用,统计表是表现数字资料整理结果的最常用的一种表格,统计表是由纵横交叉线条所绘制的表格来表现统计资料的一种形式.
16.某校图书管理员清理阅览室的课外书籍时,将其中甲、乙,丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有45本,则丙类书有 120 本.
【分析】根据甲类书籍有30本,占总数的15%即可求得总书籍数,丙类所占的比例是1﹣15%﹣45%,所占的比例乘以总数即可求得丙类书的本数.
【解答】解:总数是:45÷15%=300(本),
丙类书的本数是:300×(1﹣15%﹣45%)=300×40%=120(本)
故答案为:120.
【点评】本题考查了扇形统计图,从扇形图上可以清楚地看出各部分数量和总数量之间的关系,正确求得书籍总数是关键.
三.解答题(共8小题)
17.阅读对人成长的影响是很大的.希望中学为了了解学生课外阅读的情况,就“你最喜欢的图书类别”(只选一项)随机调查了部分学生,并将调查结果统计后绘制成如下统计表和条形统计图.
种类 频数 频率
科普 0.15
艺术 78
文学 0.59
其它 81
请你根据统计图表提供的信息解答下列问题:
(1)这次随机调查了 300 名学生;
(2)把统计表和条形统计图补充完整;
(3)为满足同学们阅读兴趣,学校图书馆准备购进新书2000册.根据调查的数据,你对购进各类书籍的数量有何建议?
【分析】(1)用科普类的频数除以科普类的频率即可得到调查的人数;
(2)用总人数减去其他小组的人数即可求得喜欢文学类的人数,从而补全统计图即可;
(3)用图书总数乘以每个小组的频率即可求得购买该类图书的数量.
【解答】解:(1)观察统计图表知道喜欢科普类的有45人,频率为0.15,
故调查的总人数为45÷0.15=300名;
(2)喜欢文学类的有300﹣45﹣78﹣81=96人,
如图所示;
种类 频数 频率
科普 45 0.15
艺术 78 0.26
文学 96 0.59
其它 81
(3)科普类书籍:300册,
艺术类书籍:520册,
文学和其他类书籍:1180册.
【点评】本题考查了条形统计图及频数统计表的知识,解题的关键是仔细的读图并从图形中整理出进一步解题的有关信息.
18.某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.
【分析】(1)由给的图象解题,根据自行车所占比例为30%,而频数分布直方图知一共有24人骑自行车上学,从而求出总人数;
(2)由扇形统计图知:步行占20%,而由(1)总人数已知,从而求出步行人数,补全频数分布直方图;
(3)自行车、步行、公交车、私家车、其他交通工具所占比例之和为100%,再由直方图具体人数来相减求解.
【解答】解:(1)被抽到的学生中,骑自行车上学的学生有24人,占整个被抽到学生总数的30%,
∴抽取学生的总数为24÷30%=80(人).
(2)被抽到的学生中,步行的人数为80×20%=16人,
直方图:
(3)被抽到的学生中,乘公交车的人数为80﹣(24+16+10+4)=26,
∴全校所有学生中乘坐公交车上学的人数约为×2400=780人.
【点评】此题考查学生根据图形数据解题的能力,考查了用样本估计总体的方法,解题时注意:从扇形图上可以清楚地看出各部分数量和总数量之间的关系.
19.2012年5月13日为母亲节,某校结合学生实际,开展了形式多样的感恩教育活动.下面图1,图2分别是该校调查部分学生是否知道母亲生日情况的扇形统计图和频数分布直方图.
根据上图信息,解答下列问题:
(1)被调查的学生中,记不清母亲生日情况的学生有 30 人;
(2)本次被调查的学生总人数有 100 ,并补全频数分布直方图2;
(3)若这所学校共有学生2400人,已知被调查的学生中,知道母亲生日的女生人数是男生人数的2倍,请你通过计算估计该校知道母亲生日的女生和男生分别有多少人?
【分析】(1)直接观察条形统计图即可找到记不清母亲生日的同学人数;
(2)用记不清母亲生日的同学人数除以其圆周角所占的百分比即可求得人数;
(3)用总人乘以其圆心角所占的百分比乘以男生活女生所占的百分比即可求得男生和女生的人数.
【解答】解:(1)观察条形统计图知道记不清母亲生日的有30人;
(2)30÷=100,
不知道母亲生日的有100×=10人,
知道母亲生日的有100﹣10﹣30=60人,
故统计图为:
(3)男生知道生日人数是:2400××=480人,
女生知道生日人数是:2400××=960人.
【点评】本题考查了频数分布表和频数分布直方图的知识,解题的关键是仔细的读图并从中找到进一步解题的有关信息.
20.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
类别 A B C D
时间t(h) t<1 1≤t<2 2≤t<3 t≥3
人数 5a 5b 5c 5d
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
【分析】(1)根据统计表可得5a+5b+5c+5d=50,a+b+c+d=10,再根据a<b<c<d,所以a≥1,b≥2,c≥3,d≥4,所以a+b+c+d≥10,a=1,b=2,c=3,d=4;
(2)计算出一年阅读的总字数÷100000,即可解答.
【解答】解:(1)5a+5b+5c+5d=50,a+b+c+d=10,
∵a<b<c<d,
∴a≥1,b≥2,c≥3,d≥4,
∴a+b+c+d≥10,
∴a=1,b=2,c=3,d=4;
(2)0.5×60×200×365÷100000=21.9≈22(或21)(本).
【点评】本题考查了统计表,解决本题的关键是从统计表中获取相关信息.
21.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
组别 分数段(x) 频数
A 0≤x<60 2
B 60≤x<70 5
C 70≤x<80 17
D 80≤x<90 a
E 90≤x≤100 b
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为 50 ,频数分布表中a的值为 12 ;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
【分析】(1)从表格中知道C组的频数为17,从扇形统计图中知道C占总体的34%,可以求出样本容量,即班级人数,D组占总人数的24%可求出a的值;
(2)从样本中可以求出优秀人数所占的百分比,用样本估计总体,估计总体中优秀人数所占总人数的百分比,进而求出人数;
(3)偏差的原因可能用样本估计总体时,由于样本容量较小,且样本不具有代表性所致.
【解答】解:(1)17÷34%=50人,a=50×24%=12人,
故答案为:50,12.
(2)样本中,优秀所占的比为:,
80000×=41600人,
答:该市本次测试成绩达到优秀的人数为41600人.
(3)用样本估计整体时,由于样本容量较小,且样本不具有代表性,可能对整体的估计存在很大的偏差.
【点评】考查扇形统计图、频率分布表的绘制方法和反应数据与整体部分之间的关系,同时理解用样本估计总体时造成偏差的原因,知道样本取样的数量、所具有代表性的重要性.
22.某中学七年级开设了艺术课程,每名学生从合唱、管弦乐、舞蹈、动漫、吉他这五门课程中选择一门进行学习.为了解学生的选择意向,从七年级随机抽取了若干名同学进行了调查,将调查得到的结果绘制成如图所示的两幅统计图(均不完整).
根据题中信息,回答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)若该校七年级一共有240名学生,请估计其中有多少人会选择合唱课程.
【分析】(1)根据选择管弦乐的有24人,所占的百分比是30%,据此即可求得抽取的总人数;
(2)利用百分比的意义求得选择舞蹈的人数,即可补全条形统计图;
(3)利用七年级学生总数乘以选择合唱课程的比例即可.
【解答】解:(1)抽取的总人数是:24÷30%=80(人);
(2)选择舞蹈的人数是:80×20%=16(人),选择合唱的人数是80﹣24﹣16﹣10﹣4=26(人),
条形统计图如下:
(3)240×=78(人).
答:估计该校七年级学生选择合唱课程的人数是78人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
23.“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?
【分析】(1)利用无所谓的家长的个数除以它所占的百分比即可得到所调查家长的总数;
(2)先计算出反对的家长的个数,再补全条形统计图,然后用360°乘以表示“赞成”的所占的百分比得到表示“赞成”的圆心角的度数;
(3)用10000乘以在样本中持“无所谓”态度的学生家长所占的百分比即可.
【解答】解:(1)80÷20%=400,
答:这次调查的家长人数为400人.
反对的家长的个数为:400﹣40﹣80=280;
如图所示:
(2)×360°=36°,
答:扇形图中表示家长“赞成”的圆心角的为36°.
(3)10000×≈2258,
答:估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约为2258人.
【点评】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来;从条形图可以很容易看出数据的大小,便于比较.
24.在结束了380课时初中阶段教学内容的教学后,唐老师计划再增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1~图2),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 36 度;
(2)图2中的a= 60 ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“图形与几何”内容?
【分析】(1)依据扇形圆心角的度数=部分占总体的百分比×360°,进行计算即可.
(2)依据数与代数的总课时数,即可得到a的值;
(3)依据“图形与几何”所占的百分比,即可得到课时数.
【解答】解:(1)(1﹣45%﹣5%﹣40%)×360°=10%×360°=36°,
故答案为:36°;
(2)a=45%×380﹣67﹣44=60;
故答案为:60;
(3)60×40%=24(课时),
∴应安排24课时复习“图形与几何”内容.
【点评】本题考查扇形统计图及相关计算.扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
一.选择题(共9小题)
1.为了考查一批日光灯管的使用寿命,从中抽取了30只进行试验,在这个问题中,下列说法正确的有( )
①总体是指这批日光灯管的全体;
②个体是指每只日光灯管的使用寿命;
③样本是指从中抽取的30只日光灯管的使用寿命;
④样本容量是30只.
A.1个 B.2个 C.3个 D.4个
2.下列调查,样本具有代表性的是( )
A.了解全校同学对课程的喜欢情况,对某班男同学进行调查
B.了解某小区居民的防火意识,对你们班同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查
3.青青的袋中有红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则青青的袋中大约有黄球( )
A.5个 B.10个 C.15个 D.30个
4.下表为某公司200名职员年龄的人数分配表,其中36~42岁及50~56岁的人数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄 22~28 29~35 36~42 43~49 50~56 57~63
次数 6 40 42 2
A.10 B.45 C.55 D.99
5.为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
A.学生参加社会实践活动时间最多的是16h
B.学生参加社会实践活动的时间大多数是l2~14h
C.学生参加社会实践活动时间不少于l0h的为84%
D.由样本可以估计全年级700人中参加社会实践活动时间为6~8h的大约有26人
6.如图,甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如图统计图:
则下面结论中不正确的是( )
A.新农村建设后,养殖收入增加了一倍
B.新农村建设后,种植收入减少
C.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
D.新农村建设后,其他收入增加了一倍以上
8.某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知乙类书有90本,则丙类书的本数是( )
A.80 B.144 C.200 D.90
9.小张一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小张一星期的鸡蛋开支占总开支的百分比为( )
A.3% B.10% C.30 D.不能确定
二.填空题(共7小题)
10.近几年,人们的环保意识逐渐增加,“白色污染”现象越来越受到人们的重视.小颖同学想了解班上同学家里在一年内丢弃废塑料袋的个数,你认为采用 方式合适一些.
11.小颖为了解家里的用电量,在5月初连续8天同一时刻观察家里的电表显示的数字,记录如下,估计小颖家5月份的总用电量是 千瓦时.
日期(号) 1 2 3 4 5 6 7 8
电表显示的数字(千瓦时) 117 120 124 129 135 138 142 145
12.有50个数据,把它们分成五组,第一、二、三、四、五组的数据个数分别是3,7,14、x、6,则第四组的频率为 .
13.为了了解某中学初三年级250名学生升学考试的数学成绩,从中抽取了50名学生的数学成绩进行分析,求得样本=93.5.下面是50名学生数学成绩的频率分布表:
分组 频数累计 频数 频率
60.5~70.5 正 3 a
70.5~80.5 正正 6 0.12
80.5~90.5 正正 9 0.18
90.5~100.5 正正正正 17 0.34
100.5~110.5 正正 b 0.2
110.5~120.5 正 5 0.1
合计 50 1
根据题中给出的条件回答下列问题:
(1)在这次抽样分析的过程中,样本是 ;
(2)频率分布表中的数据a= b= ;
(3)估计该校初三年级这次升学考试的数学平均成绩约为 分;
(4)在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为 人.
14.将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,则该班共有 人.
15.下表是某校初一(7)班20名学生某次数学成绩的统计表:若这20名学生平均成绩为a(a是整数),则a至少是 分.
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
16.某校图书管理员清理阅览室的课外书籍时,将其中甲、乙,丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有45本,则丙类书有 本.
三.解答题(共8小题)
17.阅读对人成长的影响是很大的.希望中学为了了解学生课外阅读的情况,就“你最喜欢的图书类别”(只选一项)随机调查了部分学生,并将调查结果统计后绘制成如下统计表和条形统计图.
种类 频数 频率
科普 0.15
艺术 78
文学 0.59
其它 81
请你根据统计图表提供的信息解答下列问题:
(1)这次随机调查了 名学生;
(2)把统计表和条形统计图补充完整;
(3)为满足同学们阅读兴趣,学校图书馆准备购进新书2000册.根据调查的数据,你对购进各类书籍的数量有何建议?
18.某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.
19.2012年5月13日为母亲节,某校结合学生实际,开展了形式多样的感恩教育活动.下面图1,图2分别是该校调查部分学生是否知道母亲生日情况的扇形统计图和频数分布直方图.
根据上图信息,解答下列问题:
(1)被调查的学生中,记不清母亲生日情况的学生有 人;
(2)本次被调查的学生总人数有 ,并补全频数分布直方图2;
(3)若这所学校共有学生2400人,已知被调查的学生中,知道母亲生日的女生人数是男生人数的2倍,请你通过计算估计该校知道母亲生日的女生和男生分别有多少人?
20.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
类别 A B C D
时间t(h) t<1 1≤t<2 2≤t<3 t≥3
人数 5a 5b 5c 5d
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
21.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
组别 分数段(x) 频数
A 0≤x<60 2
B 60≤x<70 5
C 70≤x<80 17
D 80≤x<90 a
E 90≤x≤100 b
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为 ,频数分布表中a的值为 ;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
22.某中学七年级开设了艺术课程,每名学生从合唱、管弦乐、舞蹈、动漫、吉他这五门课程中选择一门进行学习.为了解学生的选择意向,从七年级随机抽取了若干名同学进行了调查,将调查得到的结果绘制成如图所示的两幅统计图(均不完整).
根据题中信息,回答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)若该校七年级一共有240名学生,请估计其中有多少人会选择合唱课程.
23.“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?
24.在结束了380课时初中阶段教学内容的教学后,唐老师计划再增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1~图2),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2中的a= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“图形与几何”内容?
2020年北师大版七年级上册数学《第6章 数据的收集与整理》单元测试卷
参考答案与试题解析
一.选择题(共9小题)
1.为了考查一批日光灯管的使用寿命,从中抽取了30只进行试验,在这个问题中,下列说法正确的有( )
①总体是指这批日光灯管的全体;
②个体是指每只日光灯管的使用寿命;
③样本是指从中抽取的30只日光灯管的使用寿命;
④样本容量是30只.
A.1个 B.2个 C.3个 D.4个
【分析】本题考查的是确定总体.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”.我们在区分总体、个体、样本、样本容量这四个概念时,首先找出考查的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:本题中的总体是指这批日光灯管的全体的使用寿命,样本容量是30,所以①④不正确.
个体是指每只日光灯管的使用寿命,样本是指从中抽取的30只日光灯管的使用寿命,所以②和③正确.故选:B.
【点评】本题考查的是确定总体、个体、样本.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”
2.下列调查,样本具有代表性的是( )
A.了解全校同学对课程的喜欢情况,对某班男同学进行调查
B.了解某小区居民的防火意识,对你们班同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【解答】解:A、了解全校同学对课程的喜欢情况,对某班男同学进行调查,不具代表性、广泛性,故A错误;
B、了解某小区居民的防火意识,对你们班同学进行调查,调查不具代表性、广泛性,故B错误;
C、了解商场的平均日营业额,选在周末进行调查,调查不具有代表性、广泛性,故C错误;
D、了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查,调查具有代表性、广泛性,故D正确.
故选:D.
【点评】样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
3.青青的袋中有红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则青青的袋中大约有黄球( )
A.5个 B.10个 C.15个 D.30个
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手求解.
【解答】解:晓晓放入5个黑球后,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,故发现摸到黑球的频率为5%,
则可以由此估计袋中共有球=100(个),
说明此时袋中可能有100个球(包括5个黑球),故黄球有100×15%=15(个),
故选:C.
【点评】此题主要考查了利用频率估计概率,解答此题关键是要先计算出口袋中黑球的比例再算其个数.部分的具体数目=总体数目×相应频率.
4.下表为某公司200名职员年龄的人数分配表,其中36~42岁及50~56岁的人数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄 22~28 29~35 36~42 43~49 50~56 57~63
次数 6 40 42 2
A.10 B.45 C.55 D.99
【分析】根据图表求出36~42岁及50~56岁的职员人数,然后求出相对次数比,然后根据百分数的意义,扩大100倍即可得解.
【解答】解:由表知36~42岁及50~56岁的职员人数共有,
200﹣6﹣40﹣42﹣2=110人,
所以,a%+b%=×100%=55%,
所以a+b=55.
故选:C.
【点评】本题考查了频数分布表,本题难点在于a、b的和不是职员人数,而是相对次数比,这也是本题容易出错的地方.
5.为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
A.学生参加社会实践活动时间最多的是16h
B.学生参加社会实践活动的时间大多数是l2~14h
C.学生参加社会实践活动时间不少于l0h的为84%
D.由样本可以估计全年级700人中参加社会实践活动时间为6~8h的大约有26人
【分析】阅读频数分布直方图,根据直方图中获取的信息进行判断即可.
【解答】解:A、最后一个小组的时间范围为14~16h,但不代表一定有活动时间为16h的同学,故A错误;
B、18÷50=36%<50%,故B错误;
C、(14+18+10)÷50=84%,故C正确.
D、700×=28,故D错误.
故选:C.
【点评】本题主要考查的是频数分布直方图的认识,能够从直方图中获取有效信息是解题的关键.
6.如图,甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
【分析】甲户食品支出所占的百分率是把甲全年支出看作单位“1”,同理,乙户食品支出所占的百分率是把乙全年支出看作单位“1”,由于甲、乙两家全年支出无法确定,因此,两家食品支出的多少也无法确定.
【解答】解:∵甲、乙两户全年支出总数无法确定,
∴两户食品支出的多少也无法确定.
故选:D.
【点评】本题主要考查的是如何从扇形统计图获取信息.利用圆和扇形来表示总体和部分的关系,用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图.因此,从扇形图上只能看出各部分数量和总数量之间的关系.
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如图统计图:
则下面结论中不正确的是( )
A.新农村建设后,养殖收入增加了一倍
B.新农村建设后,种植收入减少
C.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
D.新农村建设后,其他收入增加了一倍以上
【分析】设建设前经济收入为a,建设后经济收入为2a.通过选项逐一分析新农村建设前后,经济收入情况,利用数据推出结果.
【解答】解:设建设前经济收入为a,建设后经济收入为2a.
A、建设后,养殖收入为30%×2a=60%a,
建设前,养殖收入为30%a,
故60%a÷30%a=2,故A项正确.
B、种植收入37%×2a﹣60%a=14%a>0,
故建设后,种植收入增加,故B项错误.
C、建设后,养殖收入与第三产业收入总和为(30%+28%)×2a=58%×2a,
经济收入为2a,
故(58%×2a)÷2a=58%>50%,故C项正确.
D、建设后,其他收入为5%×2a=10%a,
建设前,其他收入为4%a,
故10%a÷4%a=2.5>2,故D项正确.
故选:B.
【点评】本题主要考查扇形统计图的应用,命题的真假的判断,考查发现问题解决问题的能力.
8.某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知乙类书有90本,则丙类书的本数是( )
A.80 B.144 C.200 D.90
【分析】根据乙类书籍有90本,占总数的45%即可求得总书籍数,丙类所占的比例是1﹣15%﹣45%,所占的比例乘以总数即可求得丙类书的本数.
【解答】解:总数是:90÷45%=200(本),
丙类书的本数是:200×(1﹣15%﹣45%)=200×40%=80(本)
故选:A.
【点评】本题考查了扇形统计图,从扇形图上可以清楚地看出各部分数量和总数量之间的关系,正确求得总书籍数是关键.
9.小张一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小张一星期的鸡蛋开支占总开支的百分比为( )
A.3% B.10% C.30 D.不能确定
【分析】计算鸡蛋占食品开支的百分比,利用一星期的食品开支占总开支的百分比,即可求得一星期的鸡蛋开支占总开支的百分比.
【解答】解:根据一星期的食品开支图,可知鸡蛋占食品开支的百分比为:
×100%=10%,
∵一星期的食品开支占总开支的百分比为30%,
∴一星期的鸡蛋开支占总开支的百分比为30%×10%=3%.
故选:A.
【点评】本题主要考查了条形统计图以及扇形统计图的运用,通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
二.填空题(共7小题)
10.近几年,人们的环保意识逐渐增加,“白色污染”现象越来越受到人们的重视.小颖同学想了解班上同学家里在一年内丢弃废塑料袋的个数,你认为采用 抽样调查 方式合适一些.
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.了解班上同学家里在一年内丢弃废塑料袋的个数,考查的对象很多以及考查经费和时间都非常有限,普查就受到限制,这时就应选择抽样调查.
【解答】解:了解班上同学家里在一年内丢弃废塑料袋的个数,考查的对象很多以及考查经费和时间都非常有限,普查就受到限制,这时就应选择抽样调查.故填抽样.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
11.小颖为了解家里的用电量,在5月初连续8天同一时刻观察家里的电表显示的数字,记录如下,估计小颖家5月份的总用电量是 124 千瓦时.
日期(号) 1 2 3 4 5 6 7 8
电表显示的数字(千瓦时) 117 120 124 129 135 138 142 145
【分析】根据样本估计总体的统计思想:可先求出7天中用电量的平均数,作为5月份用电量的平均数,则一个月的用电总量即可求得.
【解答】解:31×=124(千瓦时).
【点评】统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体.
12.有50个数据,把它们分成五组,第一、二、三、四、五组的数据个数分别是3,7,14、x、6,则第四组的频率为 0.4 .
【分析】根据各小组频数之和等于数据总和,即可求得第四组的频数;再根据频率=频数÷总数,进行计算.
【解答】解:根据题意,得
第四组数据的个数x=50﹣(3+7+14+6)=20,
故第四组的频率为20÷50=0.4.
故答案为:0.4.
【点评】本题是对频率、频数灵活运用的综合考查.注意:各小组频数之和等于数据总和,各小组频率之和等于1.
13.为了了解某中学初三年级250名学生升学考试的数学成绩,从中抽取了50名学生的数学成绩进行分析,求得样本=93.5.下面是50名学生数学成绩的频率分布表:
分组 频数累计 频数 频率
60.5~70.5 正 3 a
70.5~80.5 正正 6 0.12
80.5~90.5 正正 9 0.18
90.5~100.5 正正正正 17 0.34
100.5~110.5 正正 b 0.2
110.5~120.5 正 5 0.1
合计 50 1
根据题中给出的条件回答下列问题:
(1)在这次抽样分析的过程中,样本是 50名学生的数学成绩 ;
(2)频率分布表中的数据a= 0.06 b= 10 ;
(3)估计该校初三年级这次升学考试的数学平均成绩约为 93.5 分;
(4)在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为 85 人.
【分析】(1)由于样本是总体中所抽取的一部分个体,根据已知条件即可确定题目中的样本;
(2)由于已知总人数为50,分别利用表格已知数据即可求解;
(3)利用样本估计总体的思想就可以解决问题;
(4)首先根据表格信息可以确定数学成绩在90.5~100.5的频率,然后利用样本估计总体的思想即可解决问题.
【解答】解:(1)在这次抽样分析的过程中,样本是50名学生的数学成绩;
(2)依题意得
a=3÷50=0.06,
b=0.2×50=10;
(3)∵所抽取了50名学生的数学成绩的样本=93.5
∴估计该校初三年级这次升学考试的数学平均成绩约为93.5分;
(4)依题意得初三年级数学成绩在90.5~100.5范围内的频率为0.34,
∴在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为0.34×250=85人.
【点评】此题既考查了样本估计总体的思想,也考查了正确利用频率分布表的能力,解题时首先根据表格信息可以分别确定a,b的值,然后利用样本估计总体的思想就可以解决问题.
14.将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,则该班共有 60 人.
【分析】依据各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,可得各组人数,进而得出总人数.
【解答】解:∵各组人数在频数分布直方图中的小长方形高的比依次为1:2:5:3:1,人数最多的一组有25人,
∴各组人数分别为5人、10人、25人、15人、5人,
∴总人数为:5+10+25+15+5=60(人),
故答案为:60.
【点评】本题主要考查了频数分布直方图,解题时注意:频数分布直方图中的小长方形高的比就是各组的频数之比.
15.下表是某校初一(7)班20名学生某次数学成绩的统计表:若这20名学生平均成绩为a(a是整数),则a至少是 79 分.
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
【分析】依据20名学生的总成绩为20a分列方程组,即可得到关系式a=84.5﹣x,再根据x的取值范围,即可得到a的最小取值.
【解答】解:由题可得,,
整理,得
a=84.5﹣x,
又∵x<12,且x为整数,
∴当x=11时,a的最小值为79,
故答案为:79.
【点评】本题主要考查了统计表的应用,统计表是表现数字资料整理结果的最常用的一种表格,统计表是由纵横交叉线条所绘制的表格来表现统计资料的一种形式.
16.某校图书管理员清理阅览室的课外书籍时,将其中甲、乙,丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有45本,则丙类书有 120 本.
【分析】根据甲类书籍有30本,占总数的15%即可求得总书籍数,丙类所占的比例是1﹣15%﹣45%,所占的比例乘以总数即可求得丙类书的本数.
【解答】解:总数是:45÷15%=300(本),
丙类书的本数是:300×(1﹣15%﹣45%)=300×40%=120(本)
故答案为:120.
【点评】本题考查了扇形统计图,从扇形图上可以清楚地看出各部分数量和总数量之间的关系,正确求得书籍总数是关键.
三.解答题(共8小题)
17.阅读对人成长的影响是很大的.希望中学为了了解学生课外阅读的情况,就“你最喜欢的图书类别”(只选一项)随机调查了部分学生,并将调查结果统计后绘制成如下统计表和条形统计图.
种类 频数 频率
科普 0.15
艺术 78
文学 0.59
其它 81
请你根据统计图表提供的信息解答下列问题:
(1)这次随机调查了 300 名学生;
(2)把统计表和条形统计图补充完整;
(3)为满足同学们阅读兴趣,学校图书馆准备购进新书2000册.根据调查的数据,你对购进各类书籍的数量有何建议?
【分析】(1)用科普类的频数除以科普类的频率即可得到调查的人数;
(2)用总人数减去其他小组的人数即可求得喜欢文学类的人数,从而补全统计图即可;
(3)用图书总数乘以每个小组的频率即可求得购买该类图书的数量.
【解答】解:(1)观察统计图表知道喜欢科普类的有45人,频率为0.15,
故调查的总人数为45÷0.15=300名;
(2)喜欢文学类的有300﹣45﹣78﹣81=96人,
如图所示;
种类 频数 频率
科普 45 0.15
艺术 78 0.26
文学 96 0.59
其它 81
(3)科普类书籍:300册,
艺术类书籍:520册,
文学和其他类书籍:1180册.
【点评】本题考查了条形统计图及频数统计表的知识,解题的关键是仔细的读图并从图形中整理出进一步解题的有关信息.
18.某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.
【分析】(1)由给的图象解题,根据自行车所占比例为30%,而频数分布直方图知一共有24人骑自行车上学,从而求出总人数;
(2)由扇形统计图知:步行占20%,而由(1)总人数已知,从而求出步行人数,补全频数分布直方图;
(3)自行车、步行、公交车、私家车、其他交通工具所占比例之和为100%,再由直方图具体人数来相减求解.
【解答】解:(1)被抽到的学生中,骑自行车上学的学生有24人,占整个被抽到学生总数的30%,
∴抽取学生的总数为24÷30%=80(人).
(2)被抽到的学生中,步行的人数为80×20%=16人,
直方图:
(3)被抽到的学生中,乘公交车的人数为80﹣(24+16+10+4)=26,
∴全校所有学生中乘坐公交车上学的人数约为×2400=780人.
【点评】此题考查学生根据图形数据解题的能力,考查了用样本估计总体的方法,解题时注意:从扇形图上可以清楚地看出各部分数量和总数量之间的关系.
19.2012年5月13日为母亲节,某校结合学生实际,开展了形式多样的感恩教育活动.下面图1,图2分别是该校调查部分学生是否知道母亲生日情况的扇形统计图和频数分布直方图.
根据上图信息,解答下列问题:
(1)被调查的学生中,记不清母亲生日情况的学生有 30 人;
(2)本次被调查的学生总人数有 100 ,并补全频数分布直方图2;
(3)若这所学校共有学生2400人,已知被调查的学生中,知道母亲生日的女生人数是男生人数的2倍,请你通过计算估计该校知道母亲生日的女生和男生分别有多少人?
【分析】(1)直接观察条形统计图即可找到记不清母亲生日的同学人数;
(2)用记不清母亲生日的同学人数除以其圆周角所占的百分比即可求得人数;
(3)用总人乘以其圆心角所占的百分比乘以男生活女生所占的百分比即可求得男生和女生的人数.
【解答】解:(1)观察条形统计图知道记不清母亲生日的有30人;
(2)30÷=100,
不知道母亲生日的有100×=10人,
知道母亲生日的有100﹣10﹣30=60人,
故统计图为:
(3)男生知道生日人数是:2400××=480人,
女生知道生日人数是:2400××=960人.
【点评】本题考查了频数分布表和频数分布直方图的知识,解题的关键是仔细的读图并从中找到进一步解题的有关信息.
20.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
类别 A B C D
时间t(h) t<1 1≤t<2 2≤t<3 t≥3
人数 5a 5b 5c 5d
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
【分析】(1)根据统计表可得5a+5b+5c+5d=50,a+b+c+d=10,再根据a<b<c<d,所以a≥1,b≥2,c≥3,d≥4,所以a+b+c+d≥10,a=1,b=2,c=3,d=4;
(2)计算出一年阅读的总字数÷100000,即可解答.
【解答】解:(1)5a+5b+5c+5d=50,a+b+c+d=10,
∵a<b<c<d,
∴a≥1,b≥2,c≥3,d≥4,
∴a+b+c+d≥10,
∴a=1,b=2,c=3,d=4;
(2)0.5×60×200×365÷100000=21.9≈22(或21)(本).
【点评】本题考查了统计表,解决本题的关键是从统计表中获取相关信息.
21.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
组别 分数段(x) 频数
A 0≤x<60 2
B 60≤x<70 5
C 70≤x<80 17
D 80≤x<90 a
E 90≤x≤100 b
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为 50 ,频数分布表中a的值为 12 ;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
【分析】(1)从表格中知道C组的频数为17,从扇形统计图中知道C占总体的34%,可以求出样本容量,即班级人数,D组占总人数的24%可求出a的值;
(2)从样本中可以求出优秀人数所占的百分比,用样本估计总体,估计总体中优秀人数所占总人数的百分比,进而求出人数;
(3)偏差的原因可能用样本估计总体时,由于样本容量较小,且样本不具有代表性所致.
【解答】解:(1)17÷34%=50人,a=50×24%=12人,
故答案为:50,12.
(2)样本中,优秀所占的比为:,
80000×=41600人,
答:该市本次测试成绩达到优秀的人数为41600人.
(3)用样本估计整体时,由于样本容量较小,且样本不具有代表性,可能对整体的估计存在很大的偏差.
【点评】考查扇形统计图、频率分布表的绘制方法和反应数据与整体部分之间的关系,同时理解用样本估计总体时造成偏差的原因,知道样本取样的数量、所具有代表性的重要性.
22.某中学七年级开设了艺术课程,每名学生从合唱、管弦乐、舞蹈、动漫、吉他这五门课程中选择一门进行学习.为了解学生的选择意向,从七年级随机抽取了若干名同学进行了调查,将调查得到的结果绘制成如图所示的两幅统计图(均不完整).
根据题中信息,回答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)若该校七年级一共有240名学生,请估计其中有多少人会选择合唱课程.
【分析】(1)根据选择管弦乐的有24人,所占的百分比是30%,据此即可求得抽取的总人数;
(2)利用百分比的意义求得选择舞蹈的人数,即可补全条形统计图;
(3)利用七年级学生总数乘以选择合唱课程的比例即可.
【解答】解:(1)抽取的总人数是:24÷30%=80(人);
(2)选择舞蹈的人数是:80×20%=16(人),选择合唱的人数是80﹣24﹣16﹣10﹣4=26(人),
条形统计图如下:
(3)240×=78(人).
答:估计该校七年级学生选择合唱课程的人数是78人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
23.“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?
【分析】(1)利用无所谓的家长的个数除以它所占的百分比即可得到所调查家长的总数;
(2)先计算出反对的家长的个数,再补全条形统计图,然后用360°乘以表示“赞成”的所占的百分比得到表示“赞成”的圆心角的度数;
(3)用10000乘以在样本中持“无所谓”态度的学生家长所占的百分比即可.
【解答】解:(1)80÷20%=400,
答:这次调查的家长人数为400人.
反对的家长的个数为:400﹣40﹣80=280;
如图所示:
(2)×360°=36°,
答:扇形图中表示家长“赞成”的圆心角的为36°.
(3)10000×≈2258,
答:估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约为2258人.
【点评】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来;从条形图可以很容易看出数据的大小,便于比较.
24.在结束了380课时初中阶段教学内容的教学后,唐老师计划再增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1~图2),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 36 度;
(2)图2中的a= 60 ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“图形与几何”内容?
【分析】(1)依据扇形圆心角的度数=部分占总体的百分比×360°,进行计算即可.
(2)依据数与代数的总课时数,即可得到a的值;
(3)依据“图形与几何”所占的百分比,即可得到课时数.
【解答】解:(1)(1﹣45%﹣5%﹣40%)×360°=10%×360°=36°,
故答案为:36°;
(2)a=45%×380﹣67﹣44=60;
故答案为:60;
(3)60×40%=24(课时),
∴应安排24课时复习“图形与几何”内容.
【点评】本题考查扇形统计图及相关计算.扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
