人教版八年级数学下册 17.1 勾股定理 最短路径教学课件(共20张)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 最短路径教学课件(共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
勾股定理
勾股定理的应用
最短距离问题
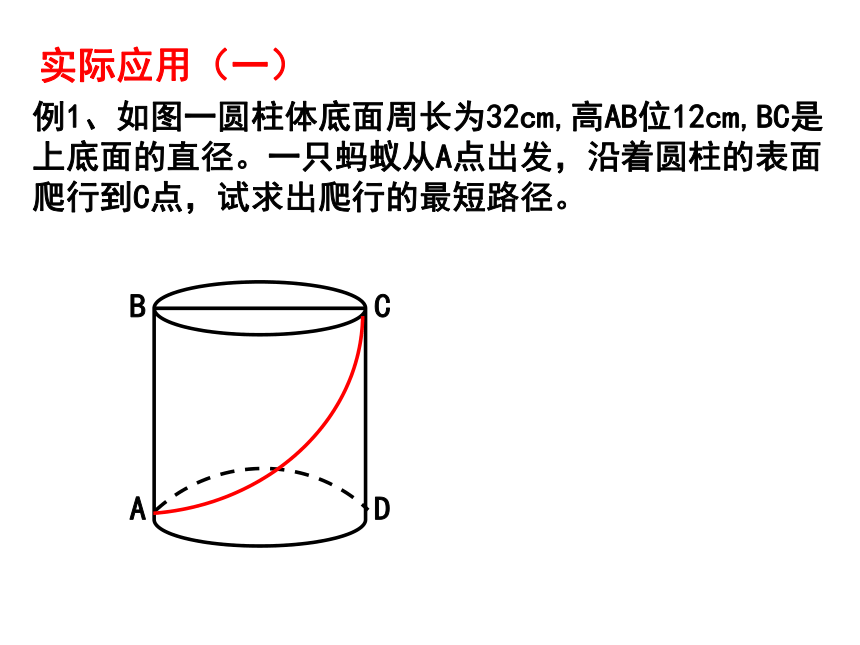
实际应用(一)
例1、如图一圆柱体底面周长为32cm,高AB位12cm,BC是
上底面的直径。一只蚂蚁从A点出发,沿着圆柱的表面
爬行到C点,试求出爬行的最短路径。
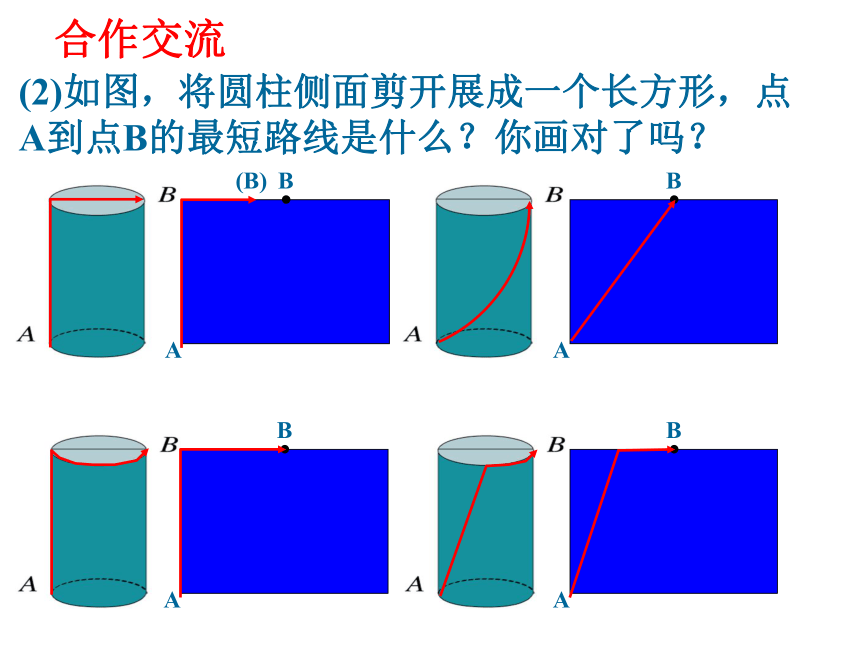
(2)如图,将圆柱侧面剪开展成一个长方形,点
A到点B的最短路线是什么?你画对了吗?
合作交流
(B)
思路小结:
圆柱体
(立体图形)
矩形
(平面图形)
直角
三角形
转化
应用勾股定理
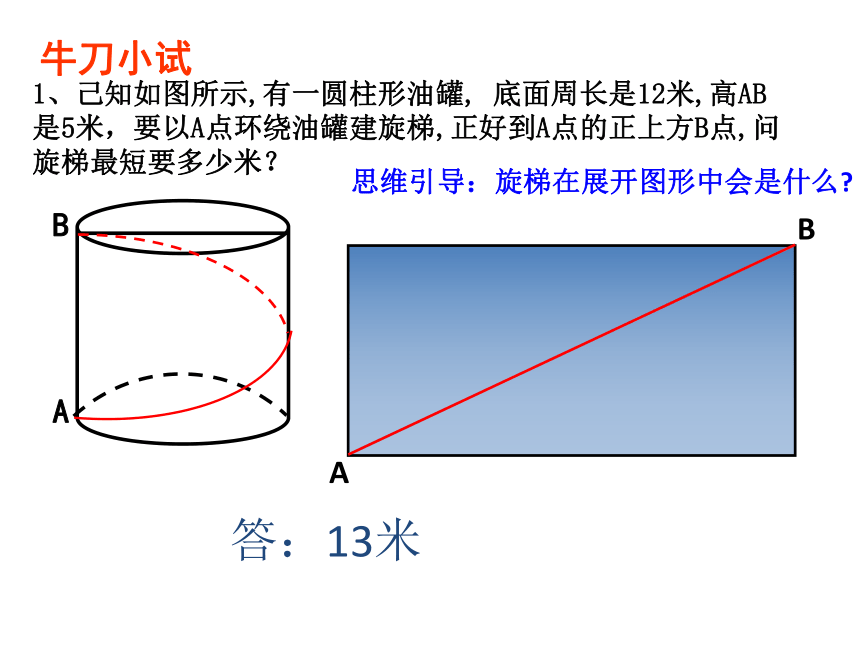
牛刀小试
1、己知如图所示,有一圆柱形油罐, 底面周长是12米,高AB
是5米,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问
旋梯最短要多少米?
思维引导:旋梯在展开图形中会是什么?
答:13米
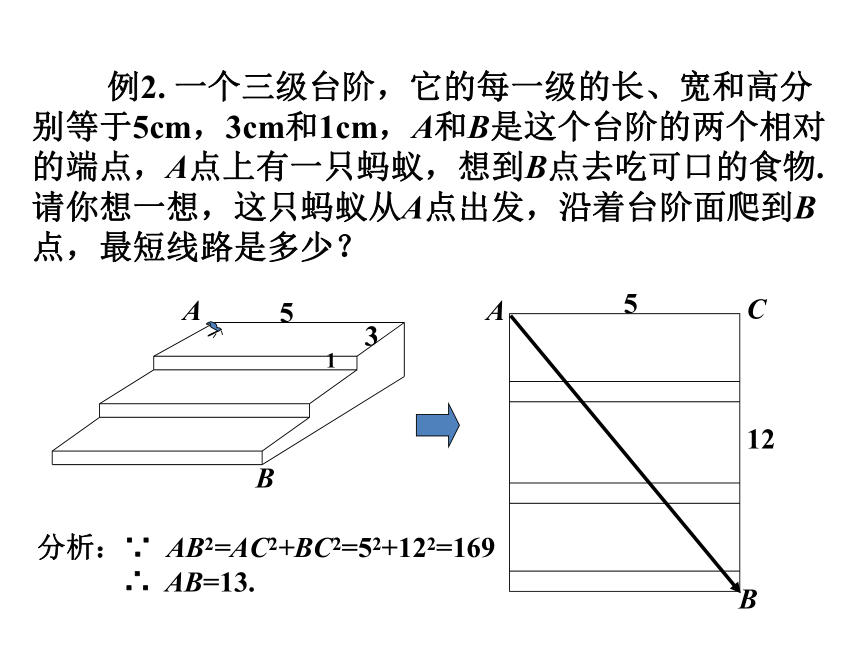
例2. 一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
5
3
1
5
12
分析:∵ AB2=AC2+BC2=52+122=169
∴ AB=13.
想一想
如果我们将例题中的圆柱体换成正方体或者长方体,情况又该怎么样呢?
例3.如果盒子换成长为4cm,宽为2cm,高为1cm的长方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路程又是多少呢?
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
C
D
E
F
G
H
?蚂蚁沿着长方体表面从注爬到B的最短距离的平方分别是:
总结提升
给出一个长方体,设它的长、宽、高分别是a、b、c,且a?
例4.如图,一个的长方体盒子的长、宽、高分别为8cm、8cm、12cm,一只蚂蚁想从盒底的点A爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短里程是多少?如果不是无盖的呢?
解:把正面和右面展开在一个平面上,
三、正方体中的最值问题
例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
学生反思:你学会了怎样的解题路?
实际问题
数学问题
直角三角形
四、课后反思
你能用上述方法快速计算下面这只蚂蚁要爬行的距离吗?
1.如图,正方体的所有而是由3x3个边长为1cm的小正方形组成.蚂蚁从底而A出沿着表而爬到右侧点B处,至少要爬行 cm.
扩展选作
2、如图,蚂蚁从地面上A点爬到墙上B点的最短路程是___________cm,其中CD=30cm,AC=23cm,BD=17cm。
3.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离的平方是多少?
?
10
20
10
20
F
E
A
E
C
B
20
15
5
4.现有 一棵树直立在地上,树高2.8丈,粗3尺,有一葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
28尺
3×7=21(尺)
聪明的葛藤
5.如图,已知圆 柱体的底面圆的半径为 ,高AB=3,AD、BC分别是两底面的直径。若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度
是 。(结果保留根式)
(该题是2006年广东省中考题改)
勾股定理
勾股定理的应用
最短距离问题
实际应用(一)
例1、如图一圆柱体底面周长为32cm,高AB位12cm,BC是
上底面的直径。一只蚂蚁从A点出发,沿着圆柱的表面
爬行到C点,试求出爬行的最短路径。
(2)如图,将圆柱侧面剪开展成一个长方形,点
A到点B的最短路线是什么?你画对了吗?
合作交流
(B)
思路小结:
圆柱体
(立体图形)
矩形
(平面图形)
直角
三角形
转化
应用勾股定理
牛刀小试
1、己知如图所示,有一圆柱形油罐, 底面周长是12米,高AB
是5米,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问
旋梯最短要多少米?
思维引导:旋梯在展开图形中会是什么?
答:13米
例2. 一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
5
3
1
5
12
分析:∵ AB2=AC2+BC2=52+122=169
∴ AB=13.
想一想
如果我们将例题中的圆柱体换成正方体或者长方体,情况又该怎么样呢?
例3.如果盒子换成长为4cm,宽为2cm,高为1cm的长方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路程又是多少呢?
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
C
D
E
F
G
H
?蚂蚁沿着长方体表面从注爬到B的最短距离的平方分别是:
总结提升
给出一个长方体,设它的长、宽、高分别是a、b、c,且a
例4.如图,一个的长方体盒子的长、宽、高分别为8cm、8cm、12cm,一只蚂蚁想从盒底的点A爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短里程是多少?如果不是无盖的呢?
解:把正面和右面展开在一个平面上,
三、正方体中的最值问题
例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
学生反思:你学会了怎样的解题路?
实际问题
数学问题
直角三角形
四、课后反思
你能用上述方法快速计算下面这只蚂蚁要爬行的距离吗?
1.如图,正方体的所有而是由3x3个边长为1cm的小正方形组成.蚂蚁从底而A出沿着表而爬到右侧点B处,至少要爬行 cm.
扩展选作
2、如图,蚂蚁从地面上A点爬到墙上B点的最短路程是___________cm,其中CD=30cm,AC=23cm,BD=17cm。
3.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离的平方是多少?
?
10
20
10
20
F
E
A
E
C
B
20
15
5
4.现有 一棵树直立在地上,树高2.8丈,粗3尺,有一葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
28尺
3×7=21(尺)
聪明的葛藤
5.如图,已知圆 柱体的底面圆的半径为 ,高AB=3,AD、BC分别是两底面的直径。若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度
是 。(结果保留根式)
(该题是2006年广东省中考题改)
