2019秋湘教版九年级数学上册第四章锐角三角函数单元测试含答案
文档属性
| 名称 | 2019秋湘教版九年级数学上册第四章锐角三角函数单元测试含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 381.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览


文档简介
2019秋湘教版九年级数学上册第四章锐角三角函数单元测试
一、单选题(共10题;共30分)
1.已知在R t △ABC中,∠C = 90°,∠A =,AB = 2,那么BC的长等于
A.???????B.?????C.?????????D.?
2.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为(?? )
A.?????B.??????C.???????D.?
3.如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是(?? )
A.??????B.????C.?????D.?
4.△ABC中,∠C=90°,BC=12,AB=13,那么sinA的值等于(????)
A.????B.????C.?????D.?
5.在△ABC中,若 +(1-tanB)2=0,则∠C的度数是(?? )
A.?45°?B.?60°??C.?75°???D.?105°
6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )
A.????B.???C.????D.?
7.小明沿着坡比为1: 的山坡向上走了600m,则他升高了(?? )
A.? m????B.?200 m??C.?300 m?????D.?200m
8.如图,在菱形ABCD中,DE⊥AB,cosA=, BE=2,则tan∠DBE的值( )
A.???B.?2??C.???D.??
9.在△ABC中,若 , 则∠C的度数为( ? ? ? ? )
A.?30°??B.?60°???C.?90°???D.?120°
10.已知α是锐角,且点A(,a),B(sinα+cosα,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是? (???)
A.?a<b<c????B.?a<c<?????C.?b<c<a??????D.?c<b<a
二、填空题(共6题;共18分)
11.如图,在△ABC中,∠C=90°,AB=8,sinA= ,则BC的长是________.
(第11题图) (第12题图) (第14题图)
12.如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.
13.已知α、β是锐角,且cotα<cotβ,则α、β中较小的角是?________.?
14.小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为________米.
15.如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=________.
(第15题图) (第16题图)
16.如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ,则 的值是________.
三、解答题(共7题;共72分)
17.计算:﹣+|﹣|+2sin45°+π0+()﹣1 .
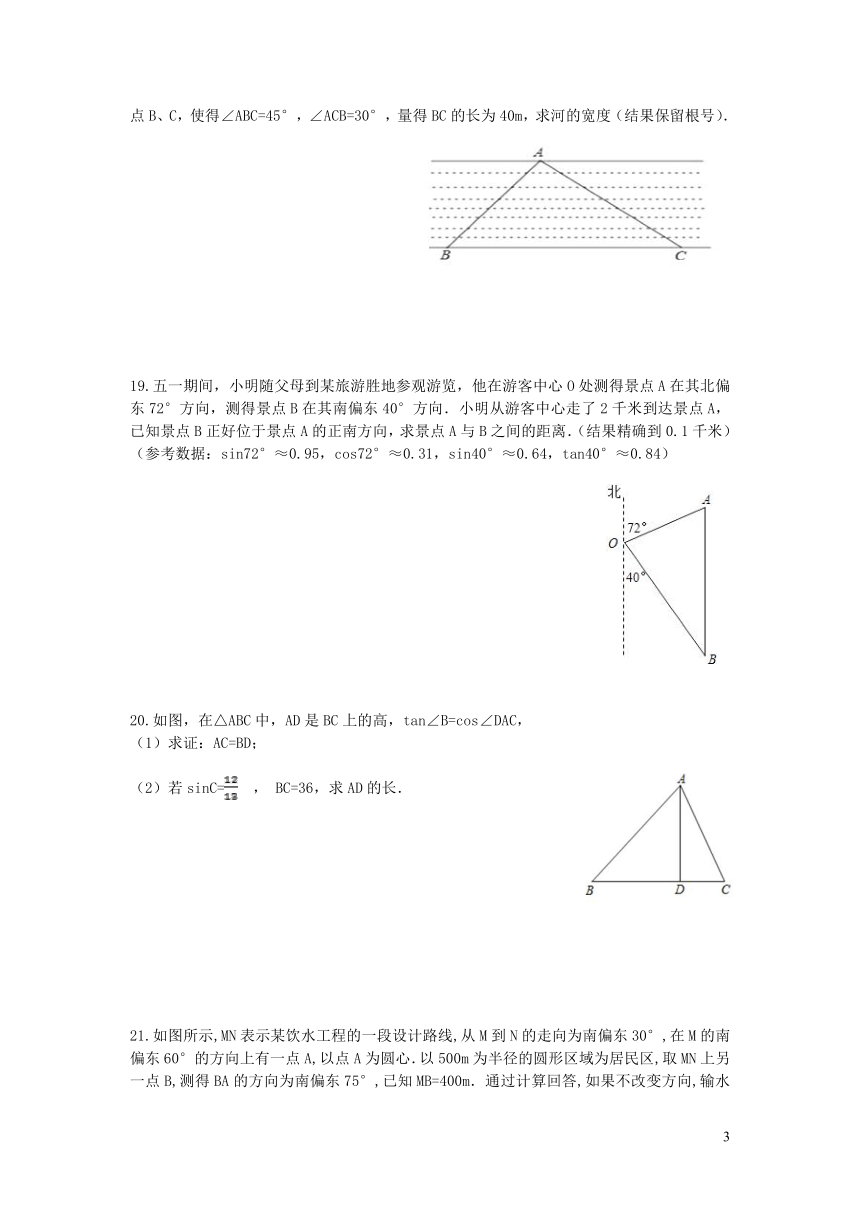
18.如图,为了求某条河的宽度,在它的对岸岸边任意取一点A,再在河的这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC的长为40m,求河的宽度(结果保留根号).
19.五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米) (参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)
20.如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC, (1)求证:AC=BD; (2)若sinC= , BC=36,求AD的长.
21.如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(≈1.73)
22.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
23.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ≈1.414, ≈1.732) ?
参考答案
1.A 2. C 3. C 4. B 5. C 6. B 7. C 8. B 9. D 10. D
11.6 12. 13. β 14. 20 15. 或7 16. 8﹣
17.解:原式=﹣2++2×+1+2=3.
18.解:作AD⊥BC,垂足为D. 设AD= xm,∵∠ABC=45°,∴BD=AD= xm,∵∠ACB=30°,∴DC= = xm,∵AD+DC=BC ,且BC=40m,∴ ,解得, , 答:则河的宽度为 m
19.解:作OC⊥AB. ∵AB∥OF,∴∠A=72°,∠B=40°,∴Rt△AOC中, AC=2×cos72°≈2×0.31=0.62(千米), OC=2×sin72°≈2×0.95=1.9(千米), 在Rt△BOC中, =tan40°,即 ≈0.84,BC≈ =2.26(千米), ∴AB=0.62+2.26=2.88(千米).
20.(1)证明:∵AD是BC上的高,∴∠ADB=∠ADC=90°,在Rt△ABD中,tanB=,在Rt△ACD中,cos∠DAC=,∵tan∠B=cos∠DAC,∴=,∴AC=BD; (2)解:在Rt△ACD中,sinC==,设AD=12k,AC=13k,∴CD==5k,∵BD=AC=13k,∴BC=BD+CD,∴13k+5k=36,解得k=2,∴AD=12×2=24.
21.解:不会穿过居民区. 理由是:如图,过A作AH⊥MN于H,作BE∥MQ,交AM于点F.
∵∠EBN=∠QMB=∠FMN=30°,∴∠NMA=30°,设AH=x,则BH=x,∴MH=AH=x,∵MH=BM+BH=x+400,∴x=x+400,∴x=200+200≈546.4>500.∴不会穿过居民区.
答:小岛A与小岛B之间的距离是100km.
22.解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF. 在Rt△BCE中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE= BC= ×1000=500米; 在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF= CD=500 米,∴DA=BE+CF=(500+500 )米, 故拦截点D处到公路的距离是(500+500 )米.
23.解:需要拆除,理由为: ∵CB⊥AB , ∠CAB=45°,∴△ABC为等腰直角三角形,∴AB=BC=10米,在Rt△BCD中,新坡面DC的坡度为i= :3,即∠CDB=30°,∴DC=2BC=20米,BD= 米,∴AD=BD-AB=(10 -10)米≈7.32米,∵3+7.32=10.32>10,
∴需要拆除 . ?
一、单选题(共10题;共30分)
1.已知在R t △ABC中,∠C = 90°,∠A =,AB = 2,那么BC的长等于
A.???????B.?????C.?????????D.?
2.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为(?? )
A.?????B.??????C.???????D.?
3.如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是(?? )
A.??????B.????C.?????D.?
4.△ABC中,∠C=90°,BC=12,AB=13,那么sinA的值等于(????)
A.????B.????C.?????D.?
5.在△ABC中,若 +(1-tanB)2=0,则∠C的度数是(?? )
A.?45°?B.?60°??C.?75°???D.?105°
6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )
A.????B.???C.????D.?
7.小明沿着坡比为1: 的山坡向上走了600m,则他升高了(?? )
A.? m????B.?200 m??C.?300 m?????D.?200m
8.如图,在菱形ABCD中,DE⊥AB,cosA=, BE=2,则tan∠DBE的值( )
A.???B.?2??C.???D.??
9.在△ABC中,若 , 则∠C的度数为( ? ? ? ? )
A.?30°??B.?60°???C.?90°???D.?120°
10.已知α是锐角,且点A(,a),B(sinα+cosα,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是? (???)
A.?a<b<c????B.?a<c<?????C.?b<c<a??????D.?c<b<a
二、填空题(共6题;共18分)
11.如图,在△ABC中,∠C=90°,AB=8,sinA= ,则BC的长是________.
(第11题图) (第12题图) (第14题图)
12.如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.
13.已知α、β是锐角,且cotα<cotβ,则α、β中较小的角是?________.?
14.小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为________米.
15.如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=________.
(第15题图) (第16题图)
16.如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ,则 的值是________.
三、解答题(共7题;共72分)
17.计算:﹣+|﹣|+2sin45°+π0+()﹣1 .
18.如图,为了求某条河的宽度,在它的对岸岸边任意取一点A,再在河的这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC的长为40m,求河的宽度(结果保留根号).
19.五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米) (参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)
20.如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC, (1)求证:AC=BD; (2)若sinC= , BC=36,求AD的长.
21.如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(≈1.73)
22.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
23.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ≈1.414, ≈1.732) ?
参考答案
1.A 2. C 3. C 4. B 5. C 6. B 7. C 8. B 9. D 10. D
11.6 12. 13. β 14. 20 15. 或7 16. 8﹣
17.解:原式=﹣2++2×+1+2=3.
18.解:作AD⊥BC,垂足为D. 设AD= xm,∵∠ABC=45°,∴BD=AD= xm,∵∠ACB=30°,∴DC= = xm,∵AD+DC=BC ,且BC=40m,∴ ,解得, , 答:则河的宽度为 m
19.解:作OC⊥AB. ∵AB∥OF,∴∠A=72°,∠B=40°,∴Rt△AOC中, AC=2×cos72°≈2×0.31=0.62(千米), OC=2×sin72°≈2×0.95=1.9(千米), 在Rt△BOC中, =tan40°,即 ≈0.84,BC≈ =2.26(千米), ∴AB=0.62+2.26=2.88(千米).
20.(1)证明:∵AD是BC上的高,∴∠ADB=∠ADC=90°,在Rt△ABD中,tanB=,在Rt△ACD中,cos∠DAC=,∵tan∠B=cos∠DAC,∴=,∴AC=BD; (2)解:在Rt△ACD中,sinC==,设AD=12k,AC=13k,∴CD==5k,∵BD=AC=13k,∴BC=BD+CD,∴13k+5k=36,解得k=2,∴AD=12×2=24.
21.解:不会穿过居民区. 理由是:如图,过A作AH⊥MN于H,作BE∥MQ,交AM于点F.
∵∠EBN=∠QMB=∠FMN=30°,∴∠NMA=30°,设AH=x,则BH=x,∴MH=AH=x,∵MH=BM+BH=x+400,∴x=x+400,∴x=200+200≈546.4>500.∴不会穿过居民区.
答:小岛A与小岛B之间的距离是100km.
22.解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF. 在Rt△BCE中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE= BC= ×1000=500米; 在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF= CD=500 米,∴DA=BE+CF=(500+500 )米, 故拦截点D处到公路的距离是(500+500 )米.
23.解:需要拆除,理由为: ∵CB⊥AB , ∠CAB=45°,∴△ABC为等腰直角三角形,∴AB=BC=10米,在Rt△BCD中,新坡面DC的坡度为i= :3,即∠CDB=30°,∴DC=2BC=20米,BD= 米,∴AD=BD-AB=(10 -10)米≈7.32米,∵3+7.32=10.32>10,
∴需要拆除 . ?
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
