6.3 一元一次方程及其解法 课件(21张PPT)
文档属性
| 名称 | 6.3 一元一次方程及其解法 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 805.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览








文档简介
课件21张PPT。一元一次方程及其解法一、复习引入?(1) a + (b–c) = ; (2) a–(b–c) = ;练习2、去括号:练习1、去括号:(3) a + (–b–c)= ; (4) a–(–b–c) = . 括号前面带“+”号,去掉括号时括号内各项都不变号. 括号前面带“–”号,去掉括号时括号内各项都变号.
(3) 4 x –3 ( 1 – x ) = ______________ .(1) 9 – ( 3x + 2 ) = ;9–3x–2(2) 2 ( x + 2 ) –1 = ______________ ;2x+4–14x–3+3xa+b–c a–b+c a–b–c a+b+c 二、学习新知与上节课求解的方程形式上有什么不同? 解:去括号,得 5 x+1 = 20 x–7 x + 3.
移项,得
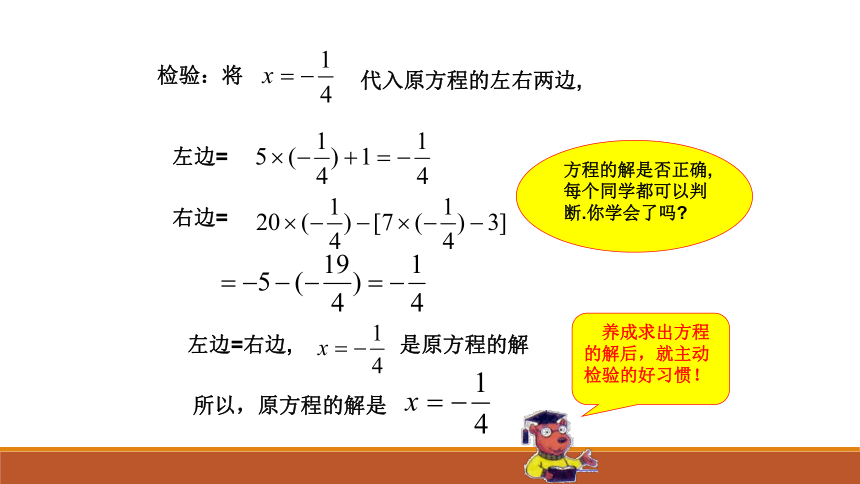
化简,得两边同除以x的系数–8,得 ,如何检查求出的方程的解是否正确? x = -4
对吗?所以原方程的解是左边=右边= 左边=右边, 是原方程的解 所以,原方程的解是 解含有“括号的”一元一次方程的一般步骤:1、去括号 2、移项3、化成形如ax=b(a≠0)的最简形式4、两边同除以未知数的系数,得到方程的解例题2 解方程:4 ( x – 2 ) + 5 = 35 – ( x – 2 )解:去括号,得4x–8+5 = 35–x+2.移项,得 4x+x = 35+2+8–5.
化简,得 5x = 40两边同时除以 x系数5,得 x = 8所以,原方程的解是 x = 8解法二:
移项,得4(x–2)+ (x–2) =35–5
化简,得5(x–2) =30
两边同除以(x–2)的系数5,得x–2=6
x=8
所以,原方程的解是x=8.例题2 解方程:4 ( x – 2 ) + 5 = 35 – ( x – 2 )三、巩固练习三、巩固练习(A组)三、巩固练习(B组)1.如果 与 互为相反数,
求 的值.
?
解:由题意得,解得,答: 的值是 . 三、巩固练习(B组)2.解方程:
?
三、巩固练习(C组)3.用不同的方法解方程:
解法一:解法二:所以,原方程的解是 .所以,原方程的解是 .四、课堂小结1、去括号法则 2、含有括号的一元一次方程的解答步骤 括号前面带“+”号,去掉括号时括号内各项都不变号. 括号前面带“–”号,去掉括号时括号内各项都要变号.3、要自觉地把方程的解代入方程左右两边进行检验,
以判断方程的解是否正确.(1)去括号 (2)移项(3)化成形如ax=b(a≠0)的最简形式(4)两边同除以未知数的系数,得到方程的解课后作业(A组)1.去括号:
2.解下列方程:
?
课后作业(A组)
此方程无解.2.解方程 ,并对
所求得的解加以检验.课后作业(A组)
检验:把 分别代入原方程的左边和右边,得 左边右边因为左边=右边,所以, 是原方程的解.课后作业(B组)1.下面的变形对不对?如果不对,指出错在哪里,并将其改正.
不对,去括号时出错,正确的是不对,去括号时出错,正确的是不对,正确的是课后作业(B组)2.如果 与 的和为1,
求 的值.
解:由题意得,答: 的值是3.解下列方程:
?
课后作业(B组)
3.在公式 中, ,
求 .
?
课后作业(C组)解:由题意得, ,
(3) 4 x –3 ( 1 – x ) = ______________ .(1) 9 – ( 3x + 2 ) = ;9–3x–2(2) 2 ( x + 2 ) –1 = ______________ ;2x+4–14x–3+3xa+b–c a–b+c a–b–c a+b+c 二、学习新知与上节课求解的方程形式上有什么不同? 解:去括号,得 5 x+1 = 20 x–7 x + 3.
移项,得
化简,得两边同除以x的系数–8,得 ,如何检查求出的方程的解是否正确? x = -4
对吗?所以原方程的解是左边=右边= 左边=右边, 是原方程的解 所以,原方程的解是 解含有“括号的”一元一次方程的一般步骤:1、去括号 2、移项3、化成形如ax=b(a≠0)的最简形式4、两边同除以未知数的系数,得到方程的解例题2 解方程:4 ( x – 2 ) + 5 = 35 – ( x – 2 )解:去括号,得4x–8+5 = 35–x+2.移项,得 4x+x = 35+2+8–5.
化简,得 5x = 40两边同时除以 x系数5,得 x = 8所以,原方程的解是 x = 8解法二:
移项,得4(x–2)+ (x–2) =35–5
化简,得5(x–2) =30
两边同除以(x–2)的系数5,得x–2=6
x=8
所以,原方程的解是x=8.例题2 解方程:4 ( x – 2 ) + 5 = 35 – ( x – 2 )三、巩固练习三、巩固练习(A组)三、巩固练习(B组)1.如果 与 互为相反数,
求 的值.
?
解:由题意得,解得,答: 的值是 . 三、巩固练习(B组)2.解方程:
?
三、巩固练习(C组)3.用不同的方法解方程:
解法一:解法二:所以,原方程的解是 .所以,原方程的解是 .四、课堂小结1、去括号法则 2、含有括号的一元一次方程的解答步骤 括号前面带“+”号,去掉括号时括号内各项都不变号. 括号前面带“–”号,去掉括号时括号内各项都要变号.3、要自觉地把方程的解代入方程左右两边进行检验,
以判断方程的解是否正确.(1)去括号 (2)移项(3)化成形如ax=b(a≠0)的最简形式(4)两边同除以未知数的系数,得到方程的解课后作业(A组)1.去括号:
2.解下列方程:
?
课后作业(A组)
此方程无解.2.解方程 ,并对
所求得的解加以检验.课后作业(A组)
检验:把 分别代入原方程的左边和右边,得 左边右边因为左边=右边,所以, 是原方程的解.课后作业(B组)1.下面的变形对不对?如果不对,指出错在哪里,并将其改正.
不对,去括号时出错,正确的是不对,去括号时出错,正确的是不对,正确的是课后作业(B组)2.如果 与 的和为1,
求 的值.
解:由题意得,答: 的值是3.解下列方程:
?
课后作业(B组)
3.在公式 中, ,
求 .
?
课后作业(C组)解:由题意得, ,
