3.2立体几何与向量方法(共46张PPT)
文档属性
| 名称 | 3.2立体几何与向量方法(共46张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览









文档简介
(共46张PPT)
3.2 立体几何与向量方法
立体几何问题,你是否已经初步体会到空间向量在解决立体几何问题中的作用?
导入新课
在本节课之前,我们把向量从平面推广到空间,并利用空间向量解决了一些
许多立体几何问题可以转化为空间向量问题,通过空间向量运算得出几何结论.
如何确定一个点在空间的位置?在空间中给一个定点,
A和一个定方向(向量),能确定一条直线在空间的位置吗?给一个定点和一个定方向(向量)能确定一个平面在空间的位置吗?
探究
O
P
3.2-1 (1)
l
a
A
P
B
3.2-1 (2)
(1)取一点O为基点,空间中任 意一点P的位置就可以用向量 来表示.如图3.2-1 (1)
(2)空间任意一条直线l的位置可以由l上的一个定点A以及一个定方向确定.如图3.2-1 (2)
b
O
P
a
l
a
A
3.2-1 (4)
3.2-1 (3)
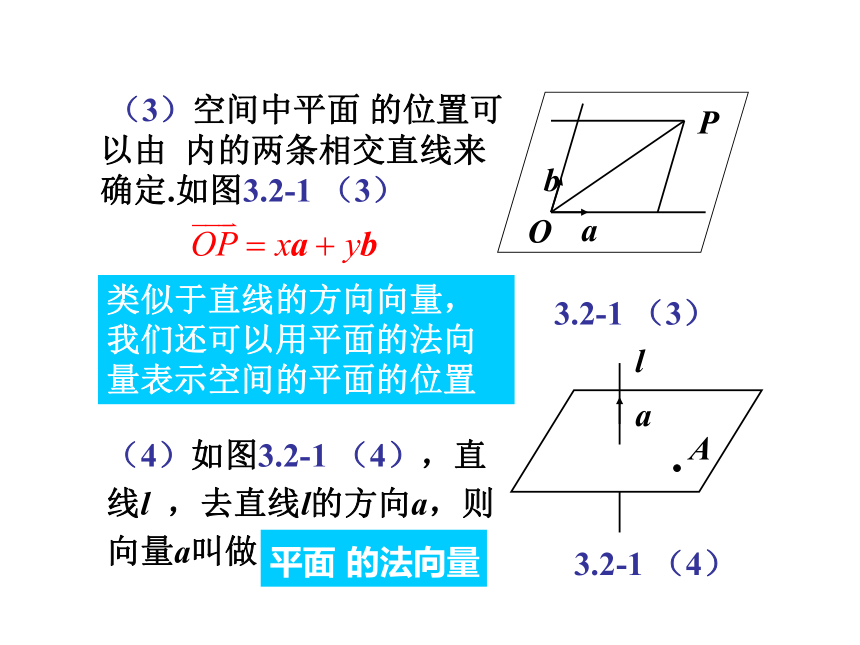
(3)空间中平面 的位置可以由 内的两条相交直线来确定.如图3.2-1 (3)
(4)如图3.2-1 (4),直线l ,去直线l的方向a,则向量a叫做
平面 的法向量
类似于直线的方向向量,我们还可以用平面的法向量表示空间的平面的位置
如果另有一条直线m,在直线m上任取向量b,b与a有什么关系?
由于方向向量与法向量可以确定直线和平面的位置,所以我们可以利用直线的方向向量与平面的法向量来表示空间直线、平面之间的平行、垂直、夹角等位置关系.
探究
一般的,由直线、平面的位置关系以及直线的方向向量和平面的法向量,可以归纳如下结论:
设直线l、m的方向向量分别为a、b,平面α,的法向量分别为u,v,则
线线平行:l //m a//b a=kb;
线面平行:l //α a⊥u a·u=0;
面面平行:α //β u//v u=kv.
线线垂直:l⊥m a⊥b a·b=0
线面垂直:l⊥ α a//u a=ku
面面垂直:α⊥β u⊥v u·v=0
线线垂直:l,m的夹角为θ (0≤θ≤)cosθ =
线面垂直:l,α的夹角为θ (0≤θ≤)sinθ =
面面垂直:α,β的夹角为θ (0≤θ≤)cosθ =
注意:
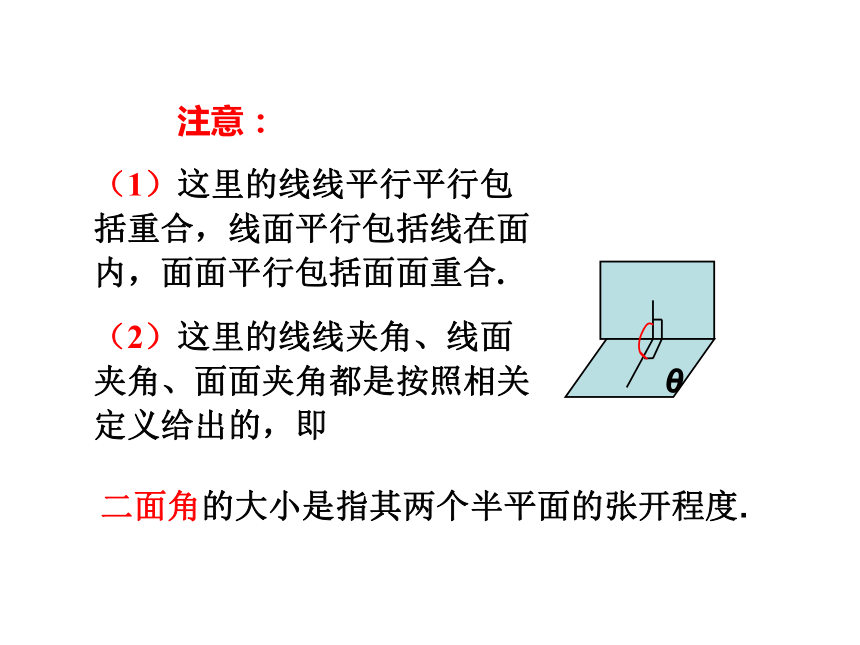
(1)这里的线线平行平行包括重合,线面平行包括线在面内,面面平行包括面面重合.
(2)这里的线线夹角、线面夹角、面面夹角都是按照相关定义给出的,即
θ
二面角的大小是指其两个半平面的张开程度.
仿照“平面与平面平行的判定定理”的证明,我们得出以下两个判定定理:
直线与平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行
平面与平面垂直的判定定理:
一个平面过另一个平面的垂线,则这两个平面垂直.
立体几何中的向量方法—“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题.
(2)进行向量运算,研究点、直线、平面之间的关系(距离和夹角等).
(3)根据运算结果的几何意义来解释相关问题.
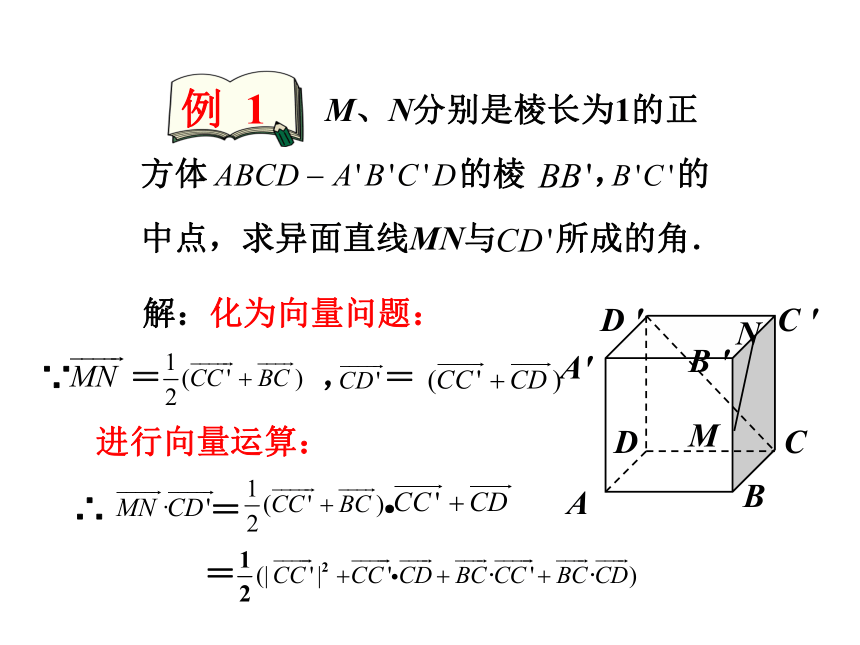
解:化为向量问题:
∵ = , =
进行向量运算:
∴ = ·
=
如图,M、N分别是棱长为1的正方体 的棱 , 的中点,求异面直线MN与 所成的角.
M
N
D
A
B
C
D ′
A′
B ′
C ′
例 1
.
∵ , , ,
∴ , ,
∴ = =
回到图形问题:
求得 cos < >
∴< >=
M
N
D
A
B
C
D ′
A′
B ′
C ′
我们同样可以用向量法求解,解答过程如下:
如右图:将F1分解为一个向上的分力F11和一个指向钢板重心的分力F12,这两个分力互相垂直.F=F1cos60°= F1,
F12=
F11=
对F2,F3可以得到同样大的向上的分力,因此合力为 .
F12
F11
F1
F
在上节课中我们提到用坐标法来解决立体几何问题,这节课,我们结合向量法和坐标法来解决例题几何问题,由于法向量对坐标法有着极其重要的作用.
让我们首先回顾法向量的定义:
法向量定义:如果直线l ⊥ α, 取直线l的方向向量为 ,则向量 叫作平面α的法向量利用法向量,可以巧妙的解决空间角度和距离.
利用法向量,可以巧妙的解决空间角度和距离.
讨论:如何利用法向量求线面角? → 面面角?
直线AB与平面α所成的角θ,可看成是向量
所在直线与平面α的法向量所在直线夹角的余角,从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角,根据两个向量所成角的余弦公式 ,我们可以得到如下
向量法的公式:
长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E、F分别是A1D1、AB的中点,O是BC1,B1C的交点. 求直线OF与平面DEF所成角的正弦.
解:以点D为空间直角坐标系的
原点,DA、DC、DD1为坐标轴
建立如图所示的空间直角坐标系.
则D(2,2,0),E(1,0,2),F(2,2,0),O(1,4,1),
C(0,4,0),设平面DEF的法向量为
例 2
则 ,而 ,
∴ ,即 ,
解得:x:y:z = -2:2:1,
∴
∵ ,而
∴
所以,直线OF与平面DEF所成角的正弦为
O
P
3.2-1 (1)
l
a
A
P
B
3.2-1 (2)
(1)取一点O为基点,空间中任 意一点P的位置就可以用向量 来表示.如图3.2-1 (1)
(2)空间任意一条直线l的位置可以由l上的一个定点A以及一个定方向确定.如图3.2-1 (2)
课堂小结
b
O
P
a
l
a
A
3.2-1 (4)
3.2-1 (3)
(3)空间中平面 的位置可以由 内的两条相交直线来确定.如图3.2-1 (3)
(4)如图3.2-1 (4),直线l ,去直线l的方向a,则向量a叫做平面的法向量
一般的,由直线、平面的位置关系以及直线的方向向量和平面的法向量,可以归纳如下结论:
设直线l、m的方向向量分别为a、b,平面α,的法向量分别为u,v,则
线线平行:l //m a//b a=kb;
线面平行:l //α a⊥u a·u=0;
面面平行:α //β u//v u=kv.
线线垂直:l⊥m a⊥b a·b=0
线面垂直:l⊥ α a//u a=ku
面面垂直:α⊥β u⊥v u·v=0
线线垂直:l,m的夹角为θ (0≤θ≤)cosθ =
线面垂直:l,α的夹角为θ (0≤θ≤)sinθ =
面面垂直:α,β的夹角为θ (0≤θ≤)cosθ =
直线与平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行
平面与平面垂直的判定定理:
一个平面过另一个平面的垂线,则这两个平面垂直.
法向量定义:如果直线l ⊥ α, 取直线l的方向向量为 ,则向量 叫作平面α的法向量利用法向量,可以巧妙的解决空间角度和距离.
立体几何中的向量方法—“三步曲”:
(1)建立立体图形与空白键向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题.
(2)进行向量运算,研究点、直线、平面之间的关系(距离和夹角等).
(3)根据运算结果的几何意义来解释相关问题.
1.(2018安徽文)如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
OA⊥底面ABCD,OA=2,M为OA的中点.
(Ⅰ)求异面直线AB与MD所成角的大;
(Ⅱ)求点B到平面OCD的距离.
高考链接
解:作AP⊥CD于点P,如图,分别以AB,AP,AO所在直线为x,y,z轴建立坐标系
(1)设AB与MD所成的角为θ
∴AB与CD所成角的大小
所成角的大小为
(2)
设平面OCD的法向量为 ,则
即 取 解得
设点B到平面OCD的距离为d,则d为
在向量 上的投影的绝对值,
所以点B到平面OCD的距离为
(Ⅰ)求证:平面PAC⊥平面ABC
(Ⅱ)求二面角M-AC-B的大小;
(Ⅲ)求三棱锥P-MAC的体积.
2. (2007四川理)如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC
所成的角为60°
解: (Ⅰ)∵
∴
又∵
∴
(Ⅱ)在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)
由题意有 ,设
解得 z0 = 1
∴
设平面MAC的一个法向量为
则 ,取x1 = 1
得
平面ABC的法向量取为
设 与 所成的角为θ,则
显然,二面角M-AC-B的平面角为锐角,
故二面角M-AC-B的平面角大小为
(Ⅲ)由(Ⅱ)知,PCMN为正方形
∴
1.下列命题中,假命题是( )
(A)若a、b是异面直线,
则α一定存在平面过a且与b平行
(B)若a、b是异面直线,
则α一定存在平面过a且与b垂直
(C)若a、b是异面直线,
则α一定存在平面与a、b所成角相等
(D)若a、b是异面直线,
则α一定存在平面与a、b的距离相等
B
课堂练习
2.下列命题中,真命题是( )
若直线m、n都平行于α则m // n
B.设α – l- β 是直二面角,若直线m ⊥ l则m ⊥ β
C.若m、n在平面α内的射影依次是一个点和一条直线,且m⊥ n,则 或n // α
D.若直线m、n是异面直线, m // α ,则n与α相交
C
二、填空题
1.已知正四棱锥P—ABCD的高为4,侧棱长与底面所成的角为60°,则该正四棱锥的侧面积是 .
2.已知α ,β, γ是三个互不重合的平面,
是一条直线,给出下列四个命题:
①若α ⊥ β , l⊥ β,则l // α
②若l ⊥ l , l // α则α ⊥ β
③若l上有两个点到α的距离相等,则l // α
④若α ⊥ β, α // γ,则γ ⊥ β
其中正确命题的序号是_______
②④
解答题
1.如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60 °,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ,求二面角E—AF—C 的余弦值.
(Ⅰ)证明:由四边形ABCD为菱形, ∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又 BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE 平面ABCD,
所以PA⊥AE.
而PA 平面PAD,AD 平面PAD
且PA∩AD=A,
所以 AE⊥平面PAD,又PD 平面PAD.
所以 AE⊥PD.
(Ⅱ)由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,所以E、F分别为BC、PC的中点,所以
A(0,0,0),B( ,-1,0)
C(C,0,0),D(0,2,0)
P(0,0,2),E( ,0,0)
F( )
所以
设平面AEF的一法向量为m(x1,y1,z1)
则 因此
取 z1=1则 m=(0,2,-1)
因为 BD⊥AC,BD⊥PA,PA∩AC=A,
所以 BD⊥平面AFC
故 为平面AFC的一法向量.
又 =(- ),
所以 cos <m, >=
因为 二面角E-AF-C为锐角,
所以所求二面角的余弦值为
2.如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB= ,BB1=2,BC=1,∠BCC1= ,求:
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
、
,
解(I)以B为原点, 、 分别为y、z轴建立空间直角坐标系. 由于BC=1,BB1=2,AB= ,∠BCC1=
在三棱柱ABC—A1B1C1中有
B(0,0,0),A(0,0, )B1(0,2,0),
设
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是异面直线AB、EB1的公垂线,
则, 故异面直线AB、EB1的距离1.
(II)由已知有
故二面角A-EB1-A1的平面角θ的大小为向量的夹角.
3.2 立体几何与向量方法
立体几何问题,你是否已经初步体会到空间向量在解决立体几何问题中的作用?
导入新课
在本节课之前,我们把向量从平面推广到空间,并利用空间向量解决了一些
许多立体几何问题可以转化为空间向量问题,通过空间向量运算得出几何结论.
如何确定一个点在空间的位置?在空间中给一个定点,
A和一个定方向(向量),能确定一条直线在空间的位置吗?给一个定点和一个定方向(向量)能确定一个平面在空间的位置吗?
探究
O
P
3.2-1 (1)
l
a
A
P
B
3.2-1 (2)
(1)取一点O为基点,空间中任 意一点P的位置就可以用向量 来表示.如图3.2-1 (1)
(2)空间任意一条直线l的位置可以由l上的一个定点A以及一个定方向确定.如图3.2-1 (2)
b
O
P
a
l
a
A
3.2-1 (4)
3.2-1 (3)
(3)空间中平面 的位置可以由 内的两条相交直线来确定.如图3.2-1 (3)
(4)如图3.2-1 (4),直线l ,去直线l的方向a,则向量a叫做
平面 的法向量
类似于直线的方向向量,我们还可以用平面的法向量表示空间的平面的位置
如果另有一条直线m,在直线m上任取向量b,b与a有什么关系?
由于方向向量与法向量可以确定直线和平面的位置,所以我们可以利用直线的方向向量与平面的法向量来表示空间直线、平面之间的平行、垂直、夹角等位置关系.
探究
一般的,由直线、平面的位置关系以及直线的方向向量和平面的法向量,可以归纳如下结论:
设直线l、m的方向向量分别为a、b,平面α,的法向量分别为u,v,则
线线平行:l //m a//b a=kb;
线面平行:l //α a⊥u a·u=0;
面面平行:α //β u//v u=kv.
线线垂直:l⊥m a⊥b a·b=0
线面垂直:l⊥ α a//u a=ku
面面垂直:α⊥β u⊥v u·v=0
线线垂直:l,m的夹角为θ (0≤θ≤)cosθ =
线面垂直:l,α的夹角为θ (0≤θ≤)sinθ =
面面垂直:α,β的夹角为θ (0≤θ≤)cosθ =
注意:
(1)这里的线线平行平行包括重合,线面平行包括线在面内,面面平行包括面面重合.
(2)这里的线线夹角、线面夹角、面面夹角都是按照相关定义给出的,即
θ
二面角的大小是指其两个半平面的张开程度.
仿照“平面与平面平行的判定定理”的证明,我们得出以下两个判定定理:
直线与平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行
平面与平面垂直的判定定理:
一个平面过另一个平面的垂线,则这两个平面垂直.
立体几何中的向量方法—“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题.
(2)进行向量运算,研究点、直线、平面之间的关系(距离和夹角等).
(3)根据运算结果的几何意义来解释相关问题.
解:化为向量问题:
∵ = , =
进行向量运算:
∴ = ·
=
如图,M、N分别是棱长为1的正方体 的棱 , 的中点,求异面直线MN与 所成的角.
M
N
D
A
B
C
D ′
A′
B ′
C ′
例 1
.
∵ , , ,
∴ , ,
∴ = =
回到图形问题:
求得 cos < >
∴< >=
M
N
D
A
B
C
D ′
A′
B ′
C ′
我们同样可以用向量法求解,解答过程如下:
如右图:将F1分解为一个向上的分力F11和一个指向钢板重心的分力F12,这两个分力互相垂直.F=F1cos60°= F1,
F12=
F11=
对F2,F3可以得到同样大的向上的分力,因此合力为 .
F12
F11
F1
F
在上节课中我们提到用坐标法来解决立体几何问题,这节课,我们结合向量法和坐标法来解决例题几何问题,由于法向量对坐标法有着极其重要的作用.
让我们首先回顾法向量的定义:
法向量定义:如果直线l ⊥ α, 取直线l的方向向量为 ,则向量 叫作平面α的法向量利用法向量,可以巧妙的解决空间角度和距离.
利用法向量,可以巧妙的解决空间角度和距离.
讨论:如何利用法向量求线面角? → 面面角?
直线AB与平面α所成的角θ,可看成是向量
所在直线与平面α的法向量所在直线夹角的余角,从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角,根据两个向量所成角的余弦公式 ,我们可以得到如下
向量法的公式:
长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E、F分别是A1D1、AB的中点,O是BC1,B1C的交点. 求直线OF与平面DEF所成角的正弦.
解:以点D为空间直角坐标系的
原点,DA、DC、DD1为坐标轴
建立如图所示的空间直角坐标系.
则D(2,2,0),E(1,0,2),F(2,2,0),O(1,4,1),
C(0,4,0),设平面DEF的法向量为
例 2
则 ,而 ,
∴ ,即 ,
解得:x:y:z = -2:2:1,
∴
∵ ,而
∴
所以,直线OF与平面DEF所成角的正弦为
O
P
3.2-1 (1)
l
a
A
P
B
3.2-1 (2)
(1)取一点O为基点,空间中任 意一点P的位置就可以用向量 来表示.如图3.2-1 (1)
(2)空间任意一条直线l的位置可以由l上的一个定点A以及一个定方向确定.如图3.2-1 (2)
课堂小结
b
O
P
a
l
a
A
3.2-1 (4)
3.2-1 (3)
(3)空间中平面 的位置可以由 内的两条相交直线来确定.如图3.2-1 (3)
(4)如图3.2-1 (4),直线l ,去直线l的方向a,则向量a叫做平面的法向量
一般的,由直线、平面的位置关系以及直线的方向向量和平面的法向量,可以归纳如下结论:
设直线l、m的方向向量分别为a、b,平面α,的法向量分别为u,v,则
线线平行:l //m a//b a=kb;
线面平行:l //α a⊥u a·u=0;
面面平行:α //β u//v u=kv.
线线垂直:l⊥m a⊥b a·b=0
线面垂直:l⊥ α a//u a=ku
面面垂直:α⊥β u⊥v u·v=0
线线垂直:l,m的夹角为θ (0≤θ≤)cosθ =
线面垂直:l,α的夹角为θ (0≤θ≤)sinθ =
面面垂直:α,β的夹角为θ (0≤θ≤)cosθ =
直线与平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行
平面与平面垂直的判定定理:
一个平面过另一个平面的垂线,则这两个平面垂直.
法向量定义:如果直线l ⊥ α, 取直线l的方向向量为 ,则向量 叫作平面α的法向量利用法向量,可以巧妙的解决空间角度和距离.
立体几何中的向量方法—“三步曲”:
(1)建立立体图形与空白键向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题.
(2)进行向量运算,研究点、直线、平面之间的关系(距离和夹角等).
(3)根据运算结果的几何意义来解释相关问题.
1.(2018安徽文)如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
OA⊥底面ABCD,OA=2,M为OA的中点.
(Ⅰ)求异面直线AB与MD所成角的大;
(Ⅱ)求点B到平面OCD的距离.
高考链接
解:作AP⊥CD于点P,如图,分别以AB,AP,AO所在直线为x,y,z轴建立坐标系
(1)设AB与MD所成的角为θ
∴AB与CD所成角的大小
所成角的大小为
(2)
设平面OCD的法向量为 ,则
即 取 解得
设点B到平面OCD的距离为d,则d为
在向量 上的投影的绝对值,
所以点B到平面OCD的距离为
(Ⅰ)求证:平面PAC⊥平面ABC
(Ⅱ)求二面角M-AC-B的大小;
(Ⅲ)求三棱锥P-MAC的体积.
2. (2007四川理)如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC
所成的角为60°
解: (Ⅰ)∵
∴
又∵
∴
(Ⅱ)在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)
由题意有 ,设
解得 z0 = 1
∴
设平面MAC的一个法向量为
则 ,取x1 = 1
得
平面ABC的法向量取为
设 与 所成的角为θ,则
显然,二面角M-AC-B的平面角为锐角,
故二面角M-AC-B的平面角大小为
(Ⅲ)由(Ⅱ)知,PCMN为正方形
∴
1.下列命题中,假命题是( )
(A)若a、b是异面直线,
则α一定存在平面过a且与b平行
(B)若a、b是异面直线,
则α一定存在平面过a且与b垂直
(C)若a、b是异面直线,
则α一定存在平面与a、b所成角相等
(D)若a、b是异面直线,
则α一定存在平面与a、b的距离相等
B
课堂练习
2.下列命题中,真命题是( )
若直线m、n都平行于α则m // n
B.设α – l- β 是直二面角,若直线m ⊥ l则m ⊥ β
C.若m、n在平面α内的射影依次是一个点和一条直线,且m⊥ n,则 或n // α
D.若直线m、n是异面直线, m // α ,则n与α相交
C
二、填空题
1.已知正四棱锥P—ABCD的高为4,侧棱长与底面所成的角为60°,则该正四棱锥的侧面积是 .
2.已知α ,β, γ是三个互不重合的平面,
是一条直线,给出下列四个命题:
①若α ⊥ β , l⊥ β,则l // α
②若l ⊥ l , l // α则α ⊥ β
③若l上有两个点到α的距离相等,则l // α
④若α ⊥ β, α // γ,则γ ⊥ β
其中正确命题的序号是_______
②④
解答题
1.如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60 °,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ,求二面角E—AF—C 的余弦值.
(Ⅰ)证明:由四边形ABCD为菱形, ∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又 BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE 平面ABCD,
所以PA⊥AE.
而PA 平面PAD,AD 平面PAD
且PA∩AD=A,
所以 AE⊥平面PAD,又PD 平面PAD.
所以 AE⊥PD.
(Ⅱ)由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,所以E、F分别为BC、PC的中点,所以
A(0,0,0),B( ,-1,0)
C(C,0,0),D(0,2,0)
P(0,0,2),E( ,0,0)
F( )
所以
设平面AEF的一法向量为m(x1,y1,z1)
则 因此
取 z1=1则 m=(0,2,-1)
因为 BD⊥AC,BD⊥PA,PA∩AC=A,
所以 BD⊥平面AFC
故 为平面AFC的一法向量.
又 =(- ),
所以 cos <m, >=
因为 二面角E-AF-C为锐角,
所以所求二面角的余弦值为
2.如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB= ,BB1=2,BC=1,∠BCC1= ,求:
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
、
,
解(I)以B为原点, 、 分别为y、z轴建立空间直角坐标系. 由于BC=1,BB1=2,AB= ,∠BCC1=
在三棱柱ABC—A1B1C1中有
B(0,0,0),A(0,0, )B1(0,2,0),
设
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是异面直线AB、EB1的公垂线,
则, 故异面直线AB、EB1的距离1.
(II)由已知有
故二面角A-EB1-A1的平面角θ的大小为向量的夹角.
