2.3.1双曲线及其标准方程(共45张PPT)
文档属性
| 名称 | 2.3.1双曲线及其标准方程(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 876.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 21:58:02 | ||
图片预览









文档简介
(共45张PPT)
2.2 双曲线
2.2.1 双曲线及其标准方程
导入新课
观察与分析
也许同学们并没有注意到,在我们所生活的大千世界里,双曲线也时常出现在我们的周围,请同学们观察以下图片…
发电厂冷却塔的外形
可口可乐的下半部
玉枕的形状
再一次认识了双曲线之后,我们将开始深入学习数学上的双曲线.
首先来看看本节双曲线的知识结构:
双曲线的定义
双曲线的标准方程
双曲线的简单几何性质
由该知识结构图可知,我们应首先学习双曲线的定义.
我们知道,与两个定点距离的和为非零常数(大于两定点间的距离)的轨迹是椭圆.那么,与两定点距离的差为非零常数的点的轨迹是什么?
如图2.3-1,取一条拉链,
拉开它的一部分,在拉开的两边的上各选择一点,分别固定在点F1,F2上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,
会得到怎样
的曲线呢?
2.3-1
这条曲线是满足下面条件的集合:
P={M||MF1|-|MF2|=常数}(左边)
P={M||MF2|-|MF1|=常数}(右边)
这两支曲线
合起来叫做
双曲线.
F
F1
F2
M
2.3-1
类比椭圆的定义,
你能给出双曲线的定义吗?
回顾旧知:
y
x
M
F1
F2
O
c
c
图2.2-1
椭圆:平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距.
M
O
F1
F2
x
y
我们把平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做
两个焦点间距离叫做
这两个定点叫做
双曲线
双曲线的焦点
双曲线的焦距
y
x
M
F1
F2
O
c
c
图2.2-1
由椭圆的定义,椭圆就是集合
P={M||MF1|+|MF2|=2a}.
类比椭圆标准方程的建立过程,你能说说应怎样选择坐标系,
建立双曲线的标准方程吗?
回顾旧知:
类比椭圆,我们根据双曲线的集合特征,选择适当的坐标系,建立双曲线的标准方程.
M
O
F1
F2
x
y
(-c,0)
(c,0)
2.3-2
如右图建立直角坐标系xOy,
使 x 轴经过两焦点F1,F2,
y轴为线段F1F2的垂直平分线.
设M(x,y)是双曲线上任意一点,
双曲线的焦距为2c(c > 0),那么焦点F1,F2的坐标分别是(-c,0),(c,0).又设点M与F1,F2得距离差的绝对值等于常数2a.
M
O
F1
F2
x
y
(-c,0)
(c,0)
2.3-2
例1:
由定义可知,双曲线就是集合
P={M||MF1|-|MF2|=2a}.
因为|MF1|= , |MF2|= ,
所以
类比建立椭圆标准方程的化简过程,
化简①,得(c2-a2)x2-a2y2=a2(c2-a2),
两边同除以(c2-a2),得
①
M
O
F1
F2
x
y
(-c,0)
(c,0)
由双曲线的定义可知2c>2a,即c>a所以c2-a2>0.类比椭圆标准方程的建立过程,
我们令c2-a2=b2,其中b>0 ,代入上式,得
②
M
O
F1
F2
x
y
(-c,0)
(c,0)
从上述过程可以看到,双曲线上任意一点的坐标都能满足方程②,以方程②的解(x, y)为坐标的点到双曲线的两个焦点的距离之差的绝对值为2a,即以该解为坐标的点都在双曲线上,由曲线与方程的关系可知,方程②是双曲线的方程我们把它叫做 它表示焦点在x轴上,焦点分别是F1(-c,0)F2(c,0)的双曲线,这里c2=a2+b2.
双曲线的标准方程
类比焦点在y轴上的椭圆,如图2.3-3,双曲线的焦点分别是F1(0,-c),F2(0,c),a,b的意义同上,这时双曲线的标准方程式什么?
此时双曲线的方程是:
这个方程也叫双曲线的标准方程.
M
F1
F2
O
x
y
已知双曲线两个焦点分别为F1(-5,0)F2(5,0),
双曲线上的一点P到F1,F2的距离差的绝对值
等于6,求双曲线的标准方程.
例2:
解:因为双曲线的焦点在 x轴上,所以设它的标准方程为
因为2a=6,2c=10,所以 a=3,c=5,所以 b2=52-32=16.
因此,双曲线的标准方程:
设动点P到两定点F1(-1,0)和F2(1,0)的距离分别为d1和d2∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.
求出动点P的轨迹的曲线方程.
y
F1
P
O
F2
P
x
例2:
解:在三角形PF1F2中,|F1F2|=2
4=d12+d22-2d1d2cos2θ (d1-d2)2+4d1d2sin2θ
(d1-d2)2=4-4λ
|d1-d2|2=4-4λ(小于2的常数)
故动点P的轨迹C是以F1,F2为焦点,实轴长
的双曲线.
方程为 .
课堂小结
M
O
F1
F2
x
y
我们把平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线,
两个焦点间距离叫做双曲线的焦距.
这两个定点叫做双曲线的焦点,
双曲线就是集合:
P={M||MF1|-|MF2|=2a}.
其中|MF1|-|MF2|=2a ,c2-a2=b2.
双曲线的标准方程:
焦点在x轴上:
M
O
F1
F2
x
y
(-c,0)
(c,0)
M
F1
F2
O
x
y
其中|MF1|-|MF2|=2a ,c2-a2=b2.
双曲线的标准方程:
焦点在y轴上:
(a>b>0)
(a>0, b>0)
椭圆、双曲线的标准方程以及它们之间的区别
椭圆 双曲线
|MF1|+|MF2|=2a |MF1|-|MF2|=±2a
a>c>0
a2-c2=b2(b>0) c>a>0
c2 - a2=b2(b>0)
(2017湖南文)已知双曲线x2-y2=2,的右焦点为F,过点F的动直线与双曲线相交于A,B两点,点C的坐标是(1,0)
(1)证明: 为常数;
(2)若动点M满足
(其中O为坐标原点),求点M的轨迹方程.
高考链接
解:由条件知F(2,0),设A( x1,y1),B(x2,y2).
(I)当AB与x轴垂直时,可设A,B的坐标分别为 , .
此时
当AB不与x轴垂直时,设直线AB的方程是
y=k(x-2)(k≠±1).
代入x2-y2-2,有(1-k2)x2+4k2+2=0.
则x1,x2是上述方程的两个实根,
所以 ,
于是
.
综上所述, 为常数
设M(x,y),则 ,
, 由 得
即
于是的中点坐标为
当不与x轴垂直时, 即
又因A,B为两点在双曲线上,所以
x12-y12=2,x22-y22=2两式相减得
(x1-y1)(x1+y1)=(y1-y2)(y1+y2) ,即
(x1-x2)(x+2)=(y1-y2)y
将 代入上式,化简得
x2-y2=4
当AB与x轴垂直时,求得M(2,0),
也满足上述方程.
所以点的轨迹方程是x2-y2=4.
(2016北京理)已知点M(-2,0),N(2,0),动点P满足条件
记动点P的轨迹为W,求W的方程.
解:由 知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长 ,又半焦距c=2,故虚半轴长
所以W的方程为
课堂练习
B.
A.
C.
D.
1.设F1,F2分别是双曲线
的左、右焦点.若点P在双曲线上,
且 ,则 ( )
B
2. 以双曲线 的右焦点为圆心,
且与其渐近线相切的圆的方程是( )
A.
B.
C.
D.
A
填空题
1.已知中心在原点的双曲线C的一个焦点是
F1(-3,0),一条渐近线的方程是
则双曲线C的方程是___________
解:设双曲线C的方程为
由题设得: 解得,
所以双曲线C的方程为
解:设双曲线方程为
(a>0,b>0)由已知得 a= ,c= 2 ,
再由a2+b2=22,得b2=1
故双曲线C的方程为
2.已知中心在原点的双曲线C的右焦点
为(2,0),右顶点为 ,
则双曲线C的方程是______________
解答题
1. AB是双曲线 x2- =1 上的两点,N(1,2)
是线段AB的中点,则直线AB的方程为
_______________
解:依题意,可设直线方程为y=k(x-1)+2
代入 x2- =1,整理得
(2-k)x2-2k(2-k)x-(2-k)2-2=0 ①
记A(x1,y1),B(x2,y2),则x1、x2是方程①的两个不同的实数根,所以2-k2≠0,
且x1+x2=
由N(1,2)是AB中点得 (x1+x2)=1
∴ k(2-k)=2-k2,解得k=1,所易知 AB的方程为y=x+1.
2.已知双曲线x2-y2=2的左、右焦点分别为F1,F2,过点F2的动直线与双曲线相交于A,B两点,若动点M满足(其中O为坐标原点)
求点M的轨迹方程.
解:由条件知F1(-2,0),F2(2,0),A(x1,y1),B(x2,y2)
设M(x,y),则 ,
由 得
即
于是AB的中点坐标为
当AB不与x轴垂直时 即
因为A,B两点在双曲线上,所以
x12-x22=2,y12-y22=2两式相减得
(x1-x2)(x1+x2)=(y1-y2)(y1+y2) 即(x1-x2)(x-4)(y1-y2)y
将 代入上式,化简得(x-6)2-y2=4,当AB与x轴垂直时,x1=x2=2,求得M(8,0),也满足上述方程.所以点的轨迹方程是 (x-6)2-y2=4
教材习题答案
1.(1) (2)
(3)解法一:因为双曲线的焦点在y轴上,所以,可设它的标准方程为
将点( 2,-5 )代入方程,得
即a2b2+4a2-25b2=0,又a2+b2=36
解方程组
令m=a2,n=b2,代入方程组,得
解得
第二组不合题意,舍去,得a2=20,b2=16
所求双曲线的标准方程为
解法二:根据双曲线的定义,有
所以
又c=6,所以b2=36-20=16.
由已知,双曲线的焦点在y轴上,所以,所求双曲线的标准方程为:
2.提示:根据椭圆中,a2-b2=c2和双曲线中a2+b2=c2的关系式分别求出椭圆、双曲线的焦点坐标.
3.由(2+m)(m+1)>0,解得m<-2,或m>-1.
2.2 双曲线
2.2.1 双曲线及其标准方程
导入新课
观察与分析
也许同学们并没有注意到,在我们所生活的大千世界里,双曲线也时常出现在我们的周围,请同学们观察以下图片…
发电厂冷却塔的外形
可口可乐的下半部
玉枕的形状
再一次认识了双曲线之后,我们将开始深入学习数学上的双曲线.
首先来看看本节双曲线的知识结构:
双曲线的定义
双曲线的标准方程
双曲线的简单几何性质
由该知识结构图可知,我们应首先学习双曲线的定义.
我们知道,与两个定点距离的和为非零常数(大于两定点间的距离)的轨迹是椭圆.那么,与两定点距离的差为非零常数的点的轨迹是什么?
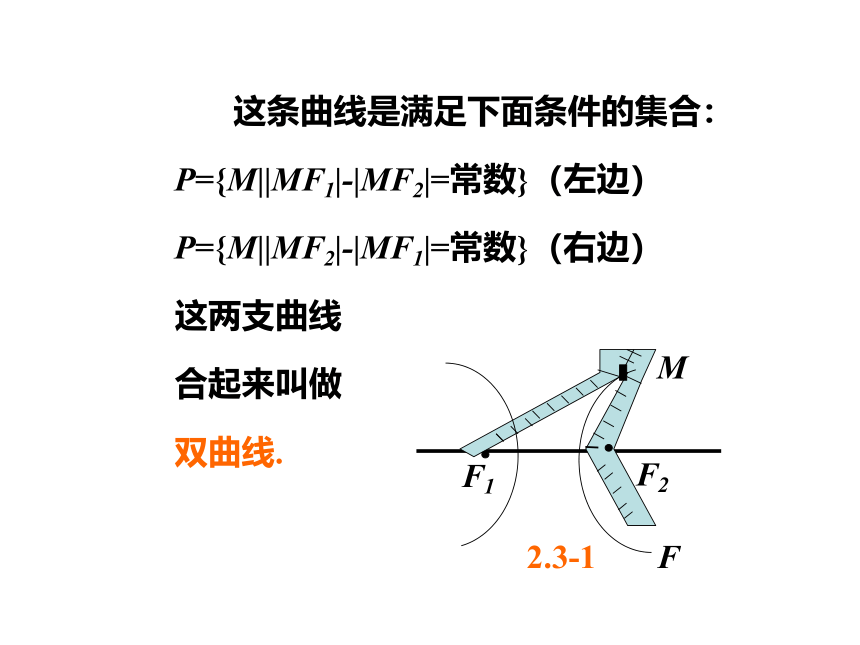
如图2.3-1,取一条拉链,
拉开它的一部分,在拉开的两边的上各选择一点,分别固定在点F1,F2上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,
会得到怎样
的曲线呢?
2.3-1
这条曲线是满足下面条件的集合:
P={M||MF1|-|MF2|=常数}(左边)
P={M||MF2|-|MF1|=常数}(右边)
这两支曲线
合起来叫做
双曲线.
F
F1
F2
M
2.3-1
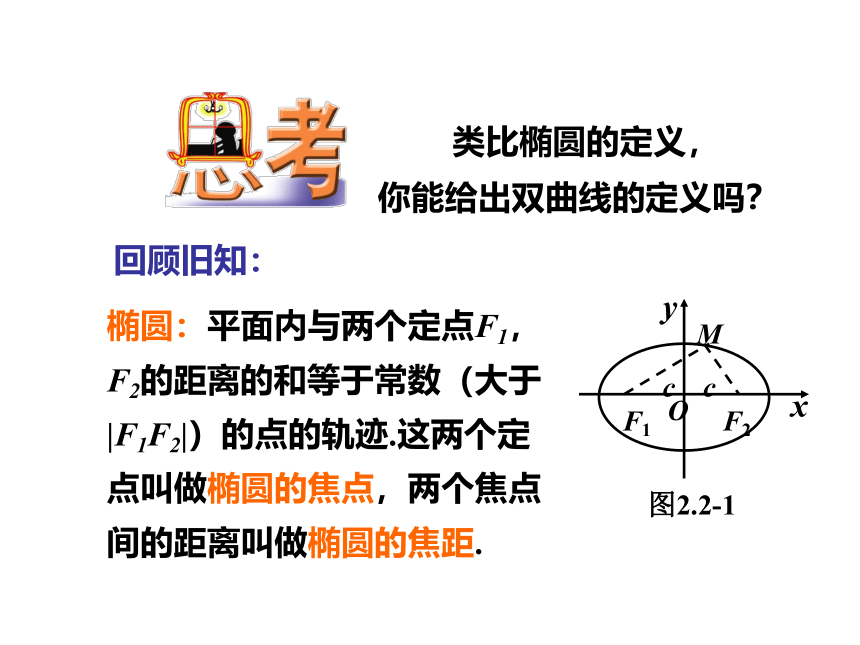
类比椭圆的定义,
你能给出双曲线的定义吗?
回顾旧知:
y
x
M
F1
F2
O
c
c
图2.2-1
椭圆:平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距.
M
O
F1
F2
x
y
我们把平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做
两个焦点间距离叫做
这两个定点叫做
双曲线
双曲线的焦点
双曲线的焦距
y
x
M
F1
F2
O
c
c
图2.2-1
由椭圆的定义,椭圆就是集合
P={M||MF1|+|MF2|=2a}.
类比椭圆标准方程的建立过程,你能说说应怎样选择坐标系,
建立双曲线的标准方程吗?
回顾旧知:
类比椭圆,我们根据双曲线的集合特征,选择适当的坐标系,建立双曲线的标准方程.
M
O
F1
F2
x
y
(-c,0)
(c,0)
2.3-2
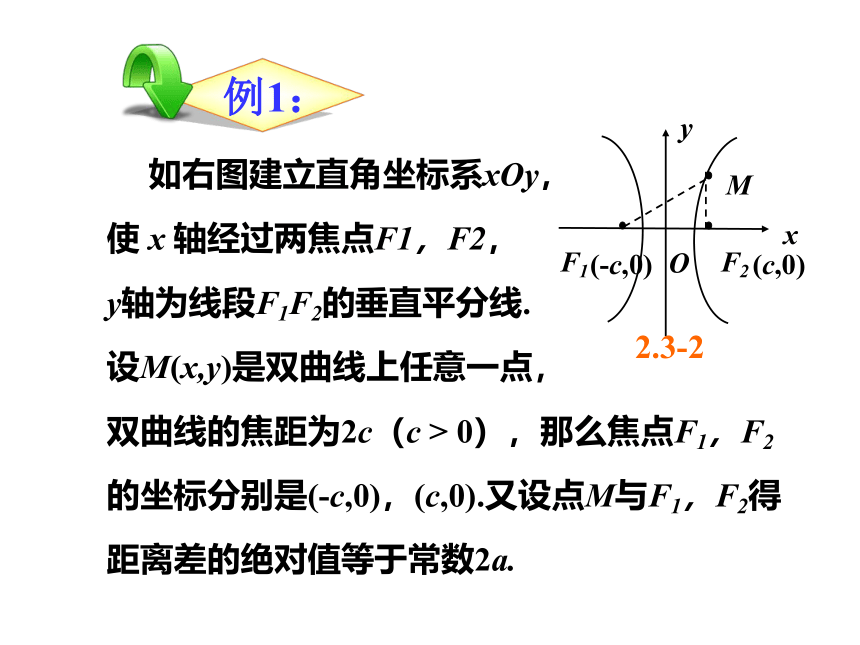
如右图建立直角坐标系xOy,
使 x 轴经过两焦点F1,F2,
y轴为线段F1F2的垂直平分线.
设M(x,y)是双曲线上任意一点,
双曲线的焦距为2c(c > 0),那么焦点F1,F2的坐标分别是(-c,0),(c,0).又设点M与F1,F2得距离差的绝对值等于常数2a.
M
O
F1
F2
x
y
(-c,0)
(c,0)
2.3-2
例1:
由定义可知,双曲线就是集合
P={M||MF1|-|MF2|=2a}.
因为|MF1|= , |MF2|= ,
所以
类比建立椭圆标准方程的化简过程,
化简①,得(c2-a2)x2-a2y2=a2(c2-a2),
两边同除以(c2-a2),得
①
M
O
F1
F2
x
y
(-c,0)
(c,0)
由双曲线的定义可知2c>2a,即c>a所以c2-a2>0.类比椭圆标准方程的建立过程,
我们令c2-a2=b2,其中b>0 ,代入上式,得
②
M
O
F1
F2
x
y
(-c,0)
(c,0)
从上述过程可以看到,双曲线上任意一点的坐标都能满足方程②,以方程②的解(x, y)为坐标的点到双曲线的两个焦点的距离之差的绝对值为2a,即以该解为坐标的点都在双曲线上,由曲线与方程的关系可知,方程②是双曲线的方程我们把它叫做 它表示焦点在x轴上,焦点分别是F1(-c,0)F2(c,0)的双曲线,这里c2=a2+b2.
双曲线的标准方程
类比焦点在y轴上的椭圆,如图2.3-3,双曲线的焦点分别是F1(0,-c),F2(0,c),a,b的意义同上,这时双曲线的标准方程式什么?
此时双曲线的方程是:
这个方程也叫双曲线的标准方程.
M
F1
F2
O
x
y
已知双曲线两个焦点分别为F1(-5,0)F2(5,0),
双曲线上的一点P到F1,F2的距离差的绝对值
等于6,求双曲线的标准方程.
例2:
解:因为双曲线的焦点在 x轴上,所以设它的标准方程为
因为2a=6,2c=10,所以 a=3,c=5,所以 b2=52-32=16.
因此,双曲线的标准方程:
设动点P到两定点F1(-1,0)和F2(1,0)的距离分别为d1和d2∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.
求出动点P的轨迹的曲线方程.
y
F1
P
O
F2
P
x
例2:
解:在三角形PF1F2中,|F1F2|=2
4=d12+d22-2d1d2cos2θ (d1-d2)2+4d1d2sin2θ
(d1-d2)2=4-4λ
|d1-d2|2=4-4λ(小于2的常数)
故动点P的轨迹C是以F1,F2为焦点,实轴长
的双曲线.
方程为 .
课堂小结
M
O
F1
F2
x
y
我们把平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线,
两个焦点间距离叫做双曲线的焦距.
这两个定点叫做双曲线的焦点,
双曲线就是集合:
P={M||MF1|-|MF2|=2a}.
其中|MF1|-|MF2|=2a ,c2-a2=b2.
双曲线的标准方程:
焦点在x轴上:
M
O
F1
F2
x
y
(-c,0)
(c,0)
M
F1
F2
O
x
y
其中|MF1|-|MF2|=2a ,c2-a2=b2.
双曲线的标准方程:
焦点在y轴上:
(a>b>0)
(a>0, b>0)
椭圆、双曲线的标准方程以及它们之间的区别
椭圆 双曲线
|MF1|+|MF2|=2a |MF1|-|MF2|=±2a
a>c>0
a2-c2=b2(b>0) c>a>0
c2 - a2=b2(b>0)
(2017湖南文)已知双曲线x2-y2=2,的右焦点为F,过点F的动直线与双曲线相交于A,B两点,点C的坐标是(1,0)
(1)证明: 为常数;
(2)若动点M满足
(其中O为坐标原点),求点M的轨迹方程.
高考链接
解:由条件知F(2,0),设A( x1,y1),B(x2,y2).
(I)当AB与x轴垂直时,可设A,B的坐标分别为 , .
此时
当AB不与x轴垂直时,设直线AB的方程是
y=k(x-2)(k≠±1).
代入x2-y2-2,有(1-k2)x2+4k2+2=0.
则x1,x2是上述方程的两个实根,
所以 ,
于是
.
综上所述, 为常数
设M(x,y),则 ,
, 由 得
即
于是的中点坐标为
当不与x轴垂直时, 即
又因A,B为两点在双曲线上,所以
x12-y12=2,x22-y22=2两式相减得
(x1-y1)(x1+y1)=(y1-y2)(y1+y2) ,即
(x1-x2)(x+2)=(y1-y2)y
将 代入上式,化简得
x2-y2=4
当AB与x轴垂直时,求得M(2,0),
也满足上述方程.
所以点的轨迹方程是x2-y2=4.
(2016北京理)已知点M(-2,0),N(2,0),动点P满足条件
记动点P的轨迹为W,求W的方程.
解:由 知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长 ,又半焦距c=2,故虚半轴长
所以W的方程为
课堂练习
B.
A.
C.
D.
1.设F1,F2分别是双曲线
的左、右焦点.若点P在双曲线上,
且 ,则 ( )
B
2. 以双曲线 的右焦点为圆心,
且与其渐近线相切的圆的方程是( )
A.
B.
C.
D.
A
填空题
1.已知中心在原点的双曲线C的一个焦点是
F1(-3,0),一条渐近线的方程是
则双曲线C的方程是___________
解:设双曲线C的方程为
由题设得: 解得,
所以双曲线C的方程为
解:设双曲线方程为
(a>0,b>0)由已知得 a= ,c= 2 ,
再由a2+b2=22,得b2=1
故双曲线C的方程为
2.已知中心在原点的双曲线C的右焦点
为(2,0),右顶点为 ,
则双曲线C的方程是______________
解答题
1. AB是双曲线 x2- =1 上的两点,N(1,2)
是线段AB的中点,则直线AB的方程为
_______________
解:依题意,可设直线方程为y=k(x-1)+2
代入 x2- =1,整理得
(2-k)x2-2k(2-k)x-(2-k)2-2=0 ①
记A(x1,y1),B(x2,y2),则x1、x2是方程①的两个不同的实数根,所以2-k2≠0,
且x1+x2=
由N(1,2)是AB中点得 (x1+x2)=1
∴ k(2-k)=2-k2,解得k=1,所易知 AB的方程为y=x+1.
2.已知双曲线x2-y2=2的左、右焦点分别为F1,F2,过点F2的动直线与双曲线相交于A,B两点,若动点M满足(其中O为坐标原点)
求点M的轨迹方程.
解:由条件知F1(-2,0),F2(2,0),A(x1,y1),B(x2,y2)
设M(x,y),则 ,
由 得
即
于是AB的中点坐标为
当AB不与x轴垂直时 即
因为A,B两点在双曲线上,所以
x12-x22=2,y12-y22=2两式相减得
(x1-x2)(x1+x2)=(y1-y2)(y1+y2) 即(x1-x2)(x-4)(y1-y2)y
将 代入上式,化简得(x-6)2-y2=4,当AB与x轴垂直时,x1=x2=2,求得M(8,0),也满足上述方程.所以点的轨迹方程是 (x-6)2-y2=4
教材习题答案
1.(1) (2)
(3)解法一:因为双曲线的焦点在y轴上,所以,可设它的标准方程为
将点( 2,-5 )代入方程,得
即a2b2+4a2-25b2=0,又a2+b2=36
解方程组
令m=a2,n=b2,代入方程组,得
解得
第二组不合题意,舍去,得a2=20,b2=16
所求双曲线的标准方程为
解法二:根据双曲线的定义,有
所以
又c=6,所以b2=36-20=16.
由已知,双曲线的焦点在y轴上,所以,所求双曲线的标准方程为:
2.提示:根据椭圆中,a2-b2=c2和双曲线中a2+b2=c2的关系式分别求出椭圆、双曲线的焦点坐标.
3.由(2+m)(m+1)>0,解得m<-2,或m>-1.
