人教新课标A版必修4 第二章《平面向量》期末复习课件(共26张PPT)
文档属性
| 名称 | 人教新课标A版必修4 第二章《平面向量》期末复习课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-03 15:46:58 | ||
图片预览







文档简介
(共26张PPT)
第二章 平面向量
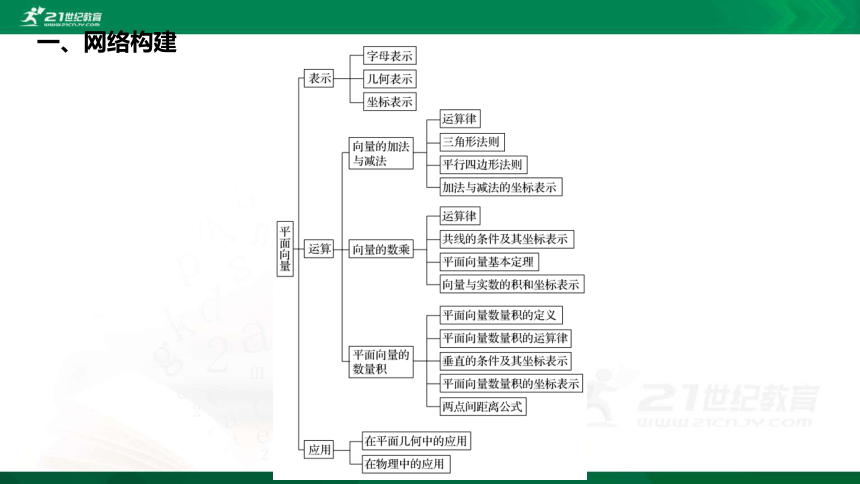
一、网络构建
二、要点归纳
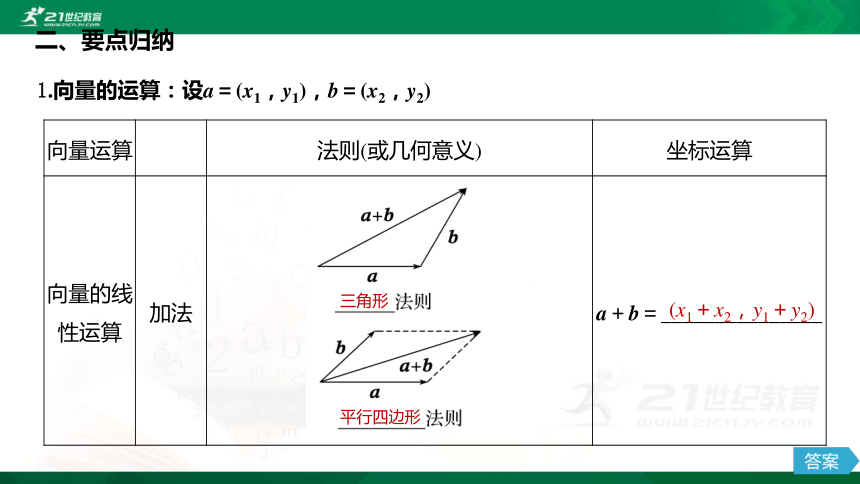
1.向量的运算:设a=(x1,y1),b=(x2,y2)
三角形
平行四边形
(x1+x2,y1+y2)
向量运算 ? 法则(或几何意义) 坐标运算
向量的线性运算 加法 a+b=_______________
三角形
(x1-x2,y1-y2)
相同
相反
(λx1,λy1)
x1x2+y1y2
向量的
线性运算 减法 a-b=_______________
数乘 (1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向 ;
当λ<0时,λa的方向与a的方向 ;
当λ=0时,λa=0 λa=_________
向量的数量积运算 a·b=|a||b|cos θ(θ为a与b的夹角),规定0·a=0,
数量积的几何意义是a的模与b在a方向上的投影的积 a·b=_________
2.两个定理
(1)平面向量基本定理
①定理:如果e1,e2是同一平面内的两个 向量,那么对于这一平面内的 向量a, 实数λ1,λ2,使a= .
②基底:把 的向量e1,e2叫做表示这一平面内 向量的一组基底.
(2)向量共线定理
向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使 .
不共线
任意
有且只有一对
λ1e1+λ2e2
不共线
所有
b=λa
3.向量的平行与垂直
a,b为非零向量,设a=(x1,y1),b=(x2,y2),
b=λa(a≠0)
a·b=0
x1x2+y1y2=0
a∥b 有唯一实数λ使得___________ x1y2-x2y1=0
a⊥b _______ _____________
2
题型探究
PART TWO
题型一 向量的线性运算
√
解析 作出示意图如图所示.
故选A.
此类平面向量的线性运算问题.求解的关键是结合图形,正确运用平面向量加减运算的三角形法则,通过对向量的逐步分解即可求得答案.
√
题型二 向量的数量积运算
(1)用k表示数量积a·b;
∴k2a2+2ka·b+b2=3a2-6ka·b+3k2b2.
∴(k2-3)a2+8ka·b+(1-3k2)b2=0.
∴k2-3+8ka·b+1-3k2=0,
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小.
又∵0°≤θ≤180°,∴θ=60°.
数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:
(1)设a=(x1,y1),b=(x2,y2),
a∥b?x1y2-x2y1=0,
a⊥b?x1x2+y1y2=0.
(2)求向量的夹角和模的问题
②两向量夹角的余弦值(0≤θ≤π,a,b为非零向量)
√
题型三 向量坐标法在平面几何中的应用
解析 以C为坐标原点,CA所在直线为x轴,CB所在直线为y轴,
建立平面直角坐标系(如图所示),
则C(0,0),A(2,0),B(0,2),所以直线AB的方程为x+y-2=0.
设M(t,2-t),则N(t+1,1-t)(0≤t≤1),
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
√
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,
3
达标检测
PART THREE
解析 如图,设对角线AC与BD交于点O,
√
1
2
3
4
5
=-2+0=-2.
A.30° B.45° C.60° D.120°
√
1
2
3
4
5
解析 设a与b的夹角为θ,
又|a-b|2=|a|2+|b|2-2a·b=1,
即1+|b|2-1=1,故|b|=1. ②
又0°≤θ≤180°,所以θ=60°,故选C.
√
1
2
3
4
5
4.已知向量a=(1,2),b=(2,-3).若向量c满足(c+a)∥b,c⊥(a+b),则c=___________.
1
2
3
4
5
解析 设c=(x,y),则c+a=(x+1,y+2).
又(c+a)∥b,∴2(y+2)+3(x+1)=0. ①
又c⊥(a+b),
∴(x,y)·(3,-1)=3x-y=0. ②
1
2
3
4
5
得a·b=0,|a|=2,|b|=1,
由x⊥y,得[a+(t2-3)b]·(-ka+tb)=0,
-ka2+ta·b-k(t2-3)a·b+t(t2-3)b2=0,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二章 平面向量
一、网络构建
二、要点归纳
1.向量的运算:设a=(x1,y1),b=(x2,y2)
三角形
平行四边形
(x1+x2,y1+y2)
向量运算 ? 法则(或几何意义) 坐标运算
向量的线性运算 加法 a+b=_______________
三角形
(x1-x2,y1-y2)
相同
相反
(λx1,λy1)
x1x2+y1y2
向量的
线性运算 减法 a-b=_______________
数乘 (1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向 ;
当λ<0时,λa的方向与a的方向 ;
当λ=0时,λa=0 λa=_________
向量的数量积运算 a·b=|a||b|cos θ(θ为a与b的夹角),规定0·a=0,
数量积的几何意义是a的模与b在a方向上的投影的积 a·b=_________
2.两个定理
(1)平面向量基本定理
①定理:如果e1,e2是同一平面内的两个 向量,那么对于这一平面内的 向量a, 实数λ1,λ2,使a= .
②基底:把 的向量e1,e2叫做表示这一平面内 向量的一组基底.
(2)向量共线定理
向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使 .
不共线
任意
有且只有一对
λ1e1+λ2e2
不共线
所有
b=λa
3.向量的平行与垂直
a,b为非零向量,设a=(x1,y1),b=(x2,y2),
b=λa(a≠0)
a·b=0
x1x2+y1y2=0
a∥b 有唯一实数λ使得___________ x1y2-x2y1=0
a⊥b _______ _____________
2
题型探究
PART TWO
题型一 向量的线性运算
√
解析 作出示意图如图所示.
故选A.
此类平面向量的线性运算问题.求解的关键是结合图形,正确运用平面向量加减运算的三角形法则,通过对向量的逐步分解即可求得答案.
√
题型二 向量的数量积运算
(1)用k表示数量积a·b;
∴k2a2+2ka·b+b2=3a2-6ka·b+3k2b2.
∴(k2-3)a2+8ka·b+(1-3k2)b2=0.
∴k2-3+8ka·b+1-3k2=0,
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小.
又∵0°≤θ≤180°,∴θ=60°.
数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:
(1)设a=(x1,y1),b=(x2,y2),
a∥b?x1y2-x2y1=0,
a⊥b?x1x2+y1y2=0.
(2)求向量的夹角和模的问题
②两向量夹角的余弦值(0≤θ≤π,a,b为非零向量)
√
题型三 向量坐标法在平面几何中的应用
解析 以C为坐标原点,CA所在直线为x轴,CB所在直线为y轴,
建立平面直角坐标系(如图所示),
则C(0,0),A(2,0),B(0,2),所以直线AB的方程为x+y-2=0.
设M(t,2-t),则N(t+1,1-t)(0≤t≤1),
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
√
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,
3
达标检测
PART THREE
解析 如图,设对角线AC与BD交于点O,
√
1
2
3
4
5
=-2+0=-2.
A.30° B.45° C.60° D.120°
√
1
2
3
4
5
解析 设a与b的夹角为θ,
又|a-b|2=|a|2+|b|2-2a·b=1,
即1+|b|2-1=1,故|b|=1. ②
又0°≤θ≤180°,所以θ=60°,故选C.
√
1
2
3
4
5
4.已知向量a=(1,2),b=(2,-3).若向量c满足(c+a)∥b,c⊥(a+b),则c=___________.
1
2
3
4
5
解析 设c=(x,y),则c+a=(x+1,y+2).
又(c+a)∥b,∴2(y+2)+3(x+1)=0. ①
又c⊥(a+b),
∴(x,y)·(3,-1)=3x-y=0. ②
1
2
3
4
5
得a·b=0,|a|=2,|b|=1,
由x⊥y,得[a+(t2-3)b]·(-ka+tb)=0,
-ka2+ta·b-k(t2-3)a·b+t(t2-3)b2=0,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
