人教新课标A版高一上册 第二章《基本初等函数》期末复习课件(共33张PPT)
文档属性
| 名称 | 人教新课标A版高一上册 第二章《基本初等函数》期末复习课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-03 16:33:34 | ||
图片预览










文档简介
(共33张PPT)
第二章 基本初等函数(I)
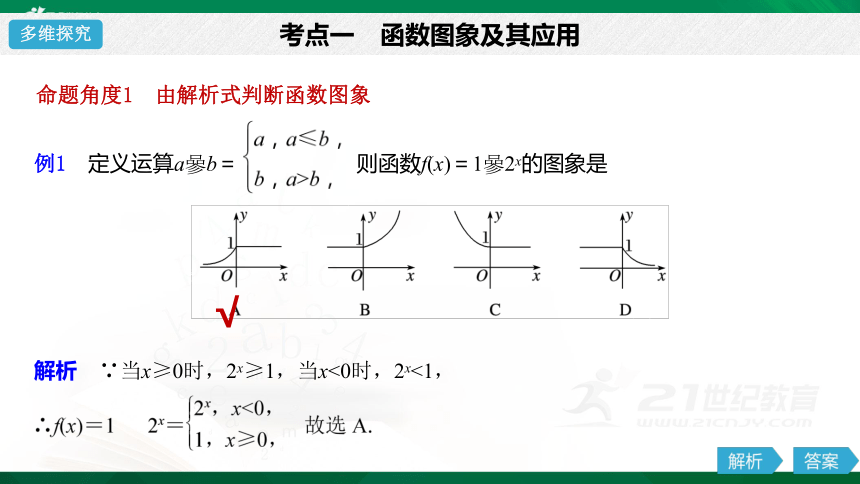
命题角度1 由解析式判断函数图象
考点一 函数图象及其应用
解析 ∵当x≥0时,2x≥1,当x<0时,2x<1,
多维探究
例1 定义运算a?b= 则函数f(x)=1?2x的图象是
√
指数函数、对数函数、幂函数合称基本初等函数(Ⅰ).其基本性质体现之一就是可以作为构成新函数的“原料”.
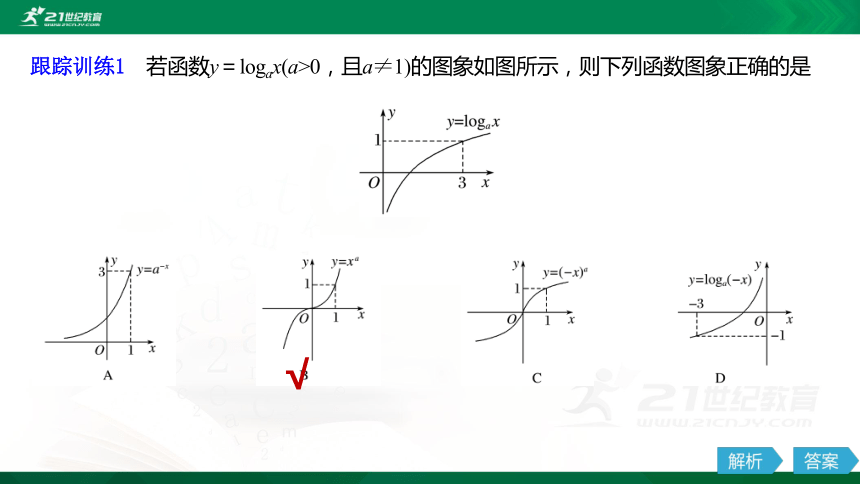
跟踪训练1 若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是
√
解析 由函数y=logax的图象过点(3,1),得a=3.选项A中的函数为y= ,则其函数图象不正确;
选项B中的函数为y=x3,则其函数图象正确;
选项C中的函数为y=(-x)3,则其函数图象不正确;
选项D中的函数为y=log3(-x),则其函数图象不正确.
命题角度2 应用函数图象特点研究性质
例2 如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是
A.{x|-1<x≤0}
B.{x|-1≤x≤1}
C.{x|-1<x≤1}
D.{x|-1<x≤2}
解析 借助函数的图象求解该不等式.
令g(x)=y=log2(x+1),作出函数g(x)图象如图.
∴结合图象知不等式f(x)≥log2(x+1)的解集为{x|-1√
指数函数、对数函数、幂函数图象既是直接考查的对象,又是数形结合求交点、最值、解不等式的工具,所以要能熟练画出这三类函数图象,并会进行平移、伸缩、对称、翻折等变换.
跟踪训练2 设函数y=x3与y= 的图象的交点坐标为(x0,y0),则x0所在的区间是
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
√
考点二 基本初等函数的性质及应用
命题角度1 比较大小
例3 (1)比较下列各组数的大小:
①27,82;
多维探究
解 ∵82=(23)2=26,
由指数函数y=2x在R上单调递增知26<27,即82<27.
②log20.4,log30.4,log40.4;
解 ∵对数函数y=log0.4x在(0,+∞)上是减函数,
∴log0.44又幂函数y=x-1在(-∞,0)上是减函数,
即log20.4(2)设x,y,z为正数,且2x=3y=5z,则
A.2x<3y<5z B.5z<2x<3y
C.3y<5z<2x D.3y<2x<5z
√
解析 设2x=3y=5z=t>1,则ln 2x=ln 3y=ln 5z=ln t>0,
∴2x>3y.类似地有2x<5z.故选D.
数的大小比较常用方法:
(1)比较两数(式)或几个数(式)大小问题是本章的一个重要题型,主要考查指数函数、对数函数、幂函数图象与性质的应用及差值比较法与商值比较法的应用.常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于0”,“大于等于0小于等于1”,“大于1”三部分,再在各部分内利用函数的性质比较大小.
跟踪训练3 比较下列各组数的大小:
(1)log0.22,log0.049;
又∵y=log0.2x在(0,+∞)上单调递减,
∴log0.22>log0.23,即log0.22>log0.049.
(2)a1.2,a1.3;
解 ∵函数y=ax(a>0,且a≠1),当底数a>1时在R上是增函数,当底数0而1.2<1.3,故当a>1时,有a1.2当0a1.3.
(3)30.4,0.43,log0.43.
解 ∵30.4>30=1,
0<0.43<0.40=1,
log0.43∴log0.43<0.43<30.4.
例4 (1)设函数f(x)=ln(2+x)-ln(2-x),则f(x)是
A.奇函数,且在(0,2)上是增函数
B.奇函数,且在(0,2)上是减函数
C.偶函数,且在(0,2)上是增函数
D.偶函数,且在(0,2)上是减函数
因为f(-x)=ln(2-x)-ln(2+x)=-f(x),关于原点对称,所以f(x)是奇函数;
又显然f(x)在(-2,2)上单调递增.
√
命题角度2 奇偶性与单调性
(2)已知 f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)
>f(- ),则a的取值范围是
解析 由f(x)是定义在R上的偶函数且在区间(-∞,0)上单调递增,可知f(x)在区间(0,+∞)上单调递减,
√
基本初等函数单调性的判断与应用
(1)对于指数函数和对数函数,注意底数a对函数单调性的影响,对于幂函数y=xα,注意指数α对函数单调性的影响.
(2)根据函数的单调性可以比较函数值的大小和求不等式的解集.
跟踪训练4 (1)下列函数中,在区间(-1,1)上为减函数的是
A.y= B.y=-x2+1
C.y=ln(x+1) D.y=2-x
解析 f(x)在R上为增函数,当x<1时,f(x)≤2恒成立,当x≥1时,令 =2得x=8.
所以x的取值范围为(-∞,8].
√
(2)设函数f(x)= 则使得f(x)≤2成立的x的取值范围是__________.
(-∞,8]
考点三 参数问题与恒成立问题
例5 已知函数f(x)=loga(8-ax)(a>0,且a≠1).
(1)若f(x)<2,求实数x的取值范围;
解 当a>1时,由f(x)<2,得0<8-ax(2)若f(x)>1在区间[1,2]上恒成立,求实数a的取值范围.
解 当a>1时,f(x)=loga(8-ax)在[1,2]上是减函数,
由f(x)>1恒成立,得f(x)min=loga(8-2a)>1,
当0由f(x)>1恒成立,得f(x)min=loga(8-a)>1,
且8-2a>0,
所以a>4,且a<4,故a不存在.
不等式恒成立问题通常转为求最大、最小值问题.如果a>f(x)恒成立,即a>f(x)max(如存在);a解 ∵函数f(x)为奇函数,
∵x∈R,∴f(0)=a+1=0,得a=-1,
(1)若函数f(x)为奇函数,求实数a的值;
∴a=-1.
解 任取x1,x2∈(-∞,+∞),且x1(2)用定义法判断函数f(x)的单调性;
由x1故f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(-∞,+∞)上是减函数.
(3)若当x∈[-1,5]时,f(x)≤0恒成立,求实数a的取值范围.
解 当x∈[-1,5]时,∵f(x)为减函数,
3
达标检测
PART THREE
1.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则f(x)的值域为
A.[9,81] B.[3,9] C.[1,9] D.[1,+∞)
1
2
3
4
5
√
解析 由f(2)=32-b=1得b=2,即f(x)=3x-2,
由2≤x≤4,得32-2≤f(x)≤34-2,
即1≤f(x)≤9.
2.化简 为
A.1 B.2 C.3 D.0
1
2
3
4
5
√
A.都是增函数
B.都是减函数
C.f(x)是增函数,g(x)是减函数
D.f(x)是减函数,g(x)是增函数
√
所以g(x)在(-∞,0)上为增函数.
1
2
3
4
5
1
2
3
4
5
Q<R<P
由函数y=2x在R上是增函数,
1
2
3
4
5
[0,+∞)
解析 当x≤1时,由21-x≤2,解得x≥0,所以0≤x≤1;
综上可知x≥0.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二章 基本初等函数(I)
命题角度1 由解析式判断函数图象
考点一 函数图象及其应用
解析 ∵当x≥0时,2x≥1,当x<0时,2x<1,
多维探究
例1 定义运算a?b= 则函数f(x)=1?2x的图象是
√
指数函数、对数函数、幂函数合称基本初等函数(Ⅰ).其基本性质体现之一就是可以作为构成新函数的“原料”.
跟踪训练1 若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是
√
解析 由函数y=logax的图象过点(3,1),得a=3.选项A中的函数为y= ,则其函数图象不正确;
选项B中的函数为y=x3,则其函数图象正确;
选项C中的函数为y=(-x)3,则其函数图象不正确;
选项D中的函数为y=log3(-x),则其函数图象不正确.
命题角度2 应用函数图象特点研究性质
例2 如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是
A.{x|-1<x≤0}
B.{x|-1≤x≤1}
C.{x|-1<x≤1}
D.{x|-1<x≤2}
解析 借助函数的图象求解该不等式.
令g(x)=y=log2(x+1),作出函数g(x)图象如图.
∴结合图象知不等式f(x)≥log2(x+1)的解集为{x|-1
指数函数、对数函数、幂函数图象既是直接考查的对象,又是数形结合求交点、最值、解不等式的工具,所以要能熟练画出这三类函数图象,并会进行平移、伸缩、对称、翻折等变换.
跟踪训练2 设函数y=x3与y= 的图象的交点坐标为(x0,y0),则x0所在的区间是
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
√
考点二 基本初等函数的性质及应用
命题角度1 比较大小
例3 (1)比较下列各组数的大小:
①27,82;
多维探究
解 ∵82=(23)2=26,
由指数函数y=2x在R上单调递增知26<27,即82<27.
②log20.4,log30.4,log40.4;
解 ∵对数函数y=log0.4x在(0,+∞)上是减函数,
∴log0.44
即log20.4
A.2x<3y<5z B.5z<2x<3y
C.3y<5z<2x D.3y<2x<5z
√
解析 设2x=3y=5z=t>1,则ln 2x=ln 3y=ln 5z=ln t>0,
∴2x>3y.类似地有2x<5z.故选D.
数的大小比较常用方法:
(1)比较两数(式)或几个数(式)大小问题是本章的一个重要题型,主要考查指数函数、对数函数、幂函数图象与性质的应用及差值比较法与商值比较法的应用.常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于0”,“大于等于0小于等于1”,“大于1”三部分,再在各部分内利用函数的性质比较大小.
跟踪训练3 比较下列各组数的大小:
(1)log0.22,log0.049;
又∵y=log0.2x在(0,+∞)上单调递减,
∴log0.22>log0.23,即log0.22>log0.049.
(2)a1.2,a1.3;
解 ∵函数y=ax(a>0,且a≠1),当底数a>1时在R上是增函数,当底数0
(3)30.4,0.43,log0.43.
解 ∵30.4>30=1,
0<0.43<0.40=1,
log0.43
例4 (1)设函数f(x)=ln(2+x)-ln(2-x),则f(x)是
A.奇函数,且在(0,2)上是增函数
B.奇函数,且在(0,2)上是减函数
C.偶函数,且在(0,2)上是增函数
D.偶函数,且在(0,2)上是减函数
因为f(-x)=ln(2-x)-ln(2+x)=-f(x),关于原点对称,所以f(x)是奇函数;
又显然f(x)在(-2,2)上单调递增.
√
命题角度2 奇偶性与单调性
(2)已知 f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)
>f(- ),则a的取值范围是
解析 由f(x)是定义在R上的偶函数且在区间(-∞,0)上单调递增,可知f(x)在区间(0,+∞)上单调递减,
√
基本初等函数单调性的判断与应用
(1)对于指数函数和对数函数,注意底数a对函数单调性的影响,对于幂函数y=xα,注意指数α对函数单调性的影响.
(2)根据函数的单调性可以比较函数值的大小和求不等式的解集.
跟踪训练4 (1)下列函数中,在区间(-1,1)上为减函数的是
A.y= B.y=-x2+1
C.y=ln(x+1) D.y=2-x
解析 f(x)在R上为增函数,当x<1时,f(x)≤2恒成立,当x≥1时,令 =2得x=8.
所以x的取值范围为(-∞,8].
√
(2)设函数f(x)= 则使得f(x)≤2成立的x的取值范围是__________.
(-∞,8]
考点三 参数问题与恒成立问题
例5 已知函数f(x)=loga(8-ax)(a>0,且a≠1).
(1)若f(x)<2,求实数x的取值范围;
解 当a>1时,由f(x)<2,得0<8-ax
解 当a>1时,f(x)=loga(8-ax)在[1,2]上是减函数,
由f(x)>1恒成立,得f(x)min=loga(8-2a)>1,
当0
且8-2a>0,
所以a>4,且a<4,故a不存在.
不等式恒成立问题通常转为求最大、最小值问题.如果a>f(x)恒成立,即a>f(x)max(如存在);a
∵x∈R,∴f(0)=a+1=0,得a=-1,
(1)若函数f(x)为奇函数,求实数a的值;
∴a=-1.
解 任取x1,x2∈(-∞,+∞),且x1
由x1
∴f(x)在(-∞,+∞)上是减函数.
(3)若当x∈[-1,5]时,f(x)≤0恒成立,求实数a的取值范围.
解 当x∈[-1,5]时,∵f(x)为减函数,
3
达标检测
PART THREE
1.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则f(x)的值域为
A.[9,81] B.[3,9] C.[1,9] D.[1,+∞)
1
2
3
4
5
√
解析 由f(2)=32-b=1得b=2,即f(x)=3x-2,
由2≤x≤4,得32-2≤f(x)≤34-2,
即1≤f(x)≤9.
2.化简 为
A.1 B.2 C.3 D.0
1
2
3
4
5
√
A.都是增函数
B.都是减函数
C.f(x)是增函数,g(x)是减函数
D.f(x)是减函数,g(x)是增函数
√
所以g(x)在(-∞,0)上为增函数.
1
2
3
4
5
1
2
3
4
5
Q<R<P
由函数y=2x在R上是增函数,
1
2
3
4
5
[0,+∞)
解析 当x≤1时,由21-x≤2,解得x≥0,所以0≤x≤1;
综上可知x≥0.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
