人教新课标A版高一上册 第三章 《函数的应用》期末复习课件(共23张PPT)
文档属性
| 名称 | 人教新课标A版高一上册 第三章 《函数的应用》期末复习课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-03 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第三章 函数的应用
例1 (1)已知y=f(x)是定义域为R的奇函数,且当x>0时,f(x)=3x+x3-5,则函数y=f(x)的零点的个数为_____.
考点一 函数的零点与方程的根的综合
解析 ∵y=f(x)是定义域为R的奇函数,∴f(0)=0,即x=0是f(x)的一个零点.
当x∈(0,+∞)时,f(x)=3x+x3-5单调递增.
又f(1)=-1<0,f(2)=12>0,
∴f(1)·f(2)<0,
∴由零点存在性定理知f(x)在(0,+∞)上只有一个零点.
故由奇函数的性质知f(x)在(-∞,0)上也只有一个零点.
综上,f(x)共有3个零点.
3
(2)函数f(x)=ln x+3x-2的零点的个数是____.
解析 由f(x)=ln x+3x-2=0,得ln x=2-3x,设g(x)=ln x,h(x)=2-3x,其图象如图所示,由图可知两个函数的图象有一个交点,故函数f(x)=ln x+3x-2有一个零点.
1
(1)函数的零点与方程的根的关系:方程f(x)=0有实数根?函数y=f(x)的图象与x轴有交点?函数y=f(x)有零点.
(2)确定函数零点的个数有两个基本方法:利用图象研究与x轴的交点个数或转化成两个函数图象的交点个数进行判断.
跟踪训练1 若函数f(x)=2x- -a的一个零点在区间(1,2)内,则实数a的取值范围是
A.(1,3) B.(1,2) C.(0,3) D.(0,2)
解析 显然f(x)在(0,+∞)上是增函数,由条件可知f(1)·f(2)<0,
即(2-2-a)(4-1-a)<0,
即a(a-3)<0,解得0<a<3.
√
考点二 函数零点的应用
例2 已知函数 f(x)= 其中m>0.若存在实数b,使得关于x的方
程f(x)=b有三个不同的实数根,则m的取值范围是__________.
解析 画出函数f(x)的图象如图所示,
(3,+∞)
由图可知,当方程f(x)=b有三个不同的根时,有4m-m2解得m>3或m<0(舍),故实数m的取值范围是(3,+∞).
解决此类题目通常用数形结合的方法.有的也可以通过解方程讨论来解决.
跟踪训练2 若函数f(x)=ax2-x-1仅有一个零点,则实数a的取值范围是_________.
解析 当a=0时,f(x)=-x-1是一次函数,有一个零点;
考点三 函数模型及应用
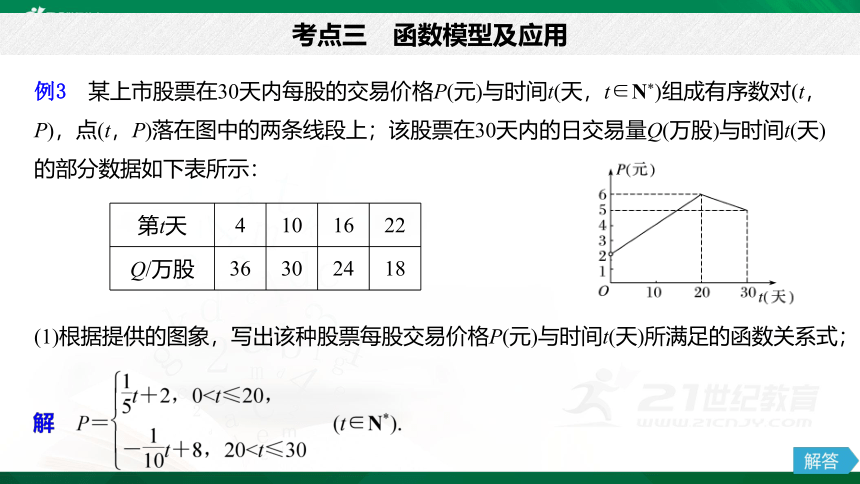
例3 某上市股票在30天内每股的交易价格P(元)与时间t(天,t∈N*)组成有序数对(t,P),点(t,P)落在图中的两条线段上;该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
第t天 4 10 16 22
Q/万股 36 30 24 18
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
解 设Q=at+b(a,b为常数且a≠0),
所以日交易量Q(万股)与时间t(天)的一次函数关系式为Q=-t+40,0(3)用y表示该股票日交易额(万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大,最大值是多少.
所以,在30天中的第15天,日交易额取得最大值125万元.
当0当20由于实际问题信息量大,有时还会出现一些陌生词,所以审题时要抓住主被动变量,围绕寻找主被动变量的关系去检索题目信息,搭建模型框架再逐步细化框架.
跟踪训练3 如图所示,A,B两城相距100 km,某天然气公司计划在两地之间建一天然气站D给A,B两城供气.已知D地距A城x km,为保证城市安全,天然气站距两城市的距离均不得小于10 km.已知建设费用y(万元)与A,B两地的供气距离的平方和成正比,当天然气站D距A城的距离为40 km时,建设费用为1 300万元.(供气距离指天然气站距某城市的距离)
(1)把建设费用y(万元)表示成供气距离x(km)的函数,并求其定义域;
解 由题意知,D地距B地(100-x)km,
设比例系数为k,则y=k[x2+(100-x)2](10≤x≤90),
又当x=40时,y=1 300,所以1 300=k(402+602),
(2)天然气供气站建在距A城多远,才能使建设费用最少?最少费用是多少?
所以当x=50时,y有最小值1 250,
所以当供气站建在距A城50 km处时,才能使建设费用最少,最少费用是1 250万元.
3
达标检测
PART THREE
1.下列函数不存在零点的是
1
2
3
4
5
解析 分别令y=0,A,B,C均有解;
√
2.已知函数f(x)= -log2x,在下列区间中,包含f(x)的零点的区间是
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)
1
2
3
4
5
√
解析 f(x)在(0,+∞)上连续,且f(2)=2>0,
1
2
3
4
5
3.若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间
A.(a,b)和(b,c)内 B.(-∞,a)和(a,b)内
C.(b,c)和(c,+∞)内 D.(-∞,a)和(c,+∞)内
√
解析 由题意a<b<c,可得f(a)=(a-b)(a-c)>0,f(b)=(b-c)·(b-a)<0,f(c)=(c-a)(c-b)>0.
显然f(a)·f(b)<0,f(b)·f(c)<0,所以该函数在(a,b)和(b,c)上均有零点,故选A.
4.设函数f(x)=log3 -a在区间(1,2)内有零点,则实数a的取值范围是_________.
1
2
3
4
5
(log32,1)
1
2
3
4
5
5.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
8
解析 由表知:汽车行驶路程为35 600-35 000=600(千米),耗油量为48升,
∴每100千米耗油量为8升.
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为____升.
加油时间 加油量(升) 加油时的累计里程(千米)
2018年5月1日 12 35 000
2018年5月15日 48 35 600
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第三章 函数的应用
例1 (1)已知y=f(x)是定义域为R的奇函数,且当x>0时,f(x)=3x+x3-5,则函数y=f(x)的零点的个数为_____.
考点一 函数的零点与方程的根的综合
解析 ∵y=f(x)是定义域为R的奇函数,∴f(0)=0,即x=0是f(x)的一个零点.
当x∈(0,+∞)时,f(x)=3x+x3-5单调递增.
又f(1)=-1<0,f(2)=12>0,
∴f(1)·f(2)<0,
∴由零点存在性定理知f(x)在(0,+∞)上只有一个零点.
故由奇函数的性质知f(x)在(-∞,0)上也只有一个零点.
综上,f(x)共有3个零点.
3
(2)函数f(x)=ln x+3x-2的零点的个数是____.
解析 由f(x)=ln x+3x-2=0,得ln x=2-3x,设g(x)=ln x,h(x)=2-3x,其图象如图所示,由图可知两个函数的图象有一个交点,故函数f(x)=ln x+3x-2有一个零点.
1
(1)函数的零点与方程的根的关系:方程f(x)=0有实数根?函数y=f(x)的图象与x轴有交点?函数y=f(x)有零点.
(2)确定函数零点的个数有两个基本方法:利用图象研究与x轴的交点个数或转化成两个函数图象的交点个数进行判断.
跟踪训练1 若函数f(x)=2x- -a的一个零点在区间(1,2)内,则实数a的取值范围是
A.(1,3) B.(1,2) C.(0,3) D.(0,2)
解析 显然f(x)在(0,+∞)上是增函数,由条件可知f(1)·f(2)<0,
即(2-2-a)(4-1-a)<0,
即a(a-3)<0,解得0<a<3.
√
考点二 函数零点的应用
例2 已知函数 f(x)= 其中m>0.若存在实数b,使得关于x的方
程f(x)=b有三个不同的实数根,则m的取值范围是__________.
解析 画出函数f(x)的图象如图所示,
(3,+∞)
由图可知,当方程f(x)=b有三个不同的根时,有4m-m2
解决此类题目通常用数形结合的方法.有的也可以通过解方程讨论来解决.
跟踪训练2 若函数f(x)=ax2-x-1仅有一个零点,则实数a的取值范围是_________.
解析 当a=0时,f(x)=-x-1是一次函数,有一个零点;
考点三 函数模型及应用
例3 某上市股票在30天内每股的交易价格P(元)与时间t(天,t∈N*)组成有序数对(t,P),点(t,P)落在图中的两条线段上;该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
第t天 4 10 16 22
Q/万股 36 30 24 18
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
解 设Q=at+b(a,b为常数且a≠0),
所以日交易量Q(万股)与时间t(天)的一次函数关系式为Q=-t+40,0
所以,在30天中的第15天,日交易额取得最大值125万元.
当0
跟踪训练3 如图所示,A,B两城相距100 km,某天然气公司计划在两地之间建一天然气站D给A,B两城供气.已知D地距A城x km,为保证城市安全,天然气站距两城市的距离均不得小于10 km.已知建设费用y(万元)与A,B两地的供气距离的平方和成正比,当天然气站D距A城的距离为40 km时,建设费用为1 300万元.(供气距离指天然气站距某城市的距离)
(1)把建设费用y(万元)表示成供气距离x(km)的函数,并求其定义域;
解 由题意知,D地距B地(100-x)km,
设比例系数为k,则y=k[x2+(100-x)2](10≤x≤90),
又当x=40时,y=1 300,所以1 300=k(402+602),
(2)天然气供气站建在距A城多远,才能使建设费用最少?最少费用是多少?
所以当x=50时,y有最小值1 250,
所以当供气站建在距A城50 km处时,才能使建设费用最少,最少费用是1 250万元.
3
达标检测
PART THREE
1.下列函数不存在零点的是
1
2
3
4
5
解析 分别令y=0,A,B,C均有解;
√
2.已知函数f(x)= -log2x,在下列区间中,包含f(x)的零点的区间是
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)
1
2
3
4
5
√
解析 f(x)在(0,+∞)上连续,且f(2)=2>0,
1
2
3
4
5
3.若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间
A.(a,b)和(b,c)内 B.(-∞,a)和(a,b)内
C.(b,c)和(c,+∞)内 D.(-∞,a)和(c,+∞)内
√
解析 由题意a<b<c,可得f(a)=(a-b)(a-c)>0,f(b)=(b-c)·(b-a)<0,f(c)=(c-a)(c-b)>0.
显然f(a)·f(b)<0,f(b)·f(c)<0,所以该函数在(a,b)和(b,c)上均有零点,故选A.
4.设函数f(x)=log3 -a在区间(1,2)内有零点,则实数a的取值范围是_________.
1
2
3
4
5
(log32,1)
1
2
3
4
5
5.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
8
解析 由表知:汽车行驶路程为35 600-35 000=600(千米),耗油量为48升,
∴每100千米耗油量为8升.
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为____升.
加油时间 加油量(升) 加油时的累计里程(千米)
2018年5月1日 12 35 000
2018年5月15日 48 35 600
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
