人教版七年级下册数学 5.2.2平行线的判定 同步练习(解析版)
文档属性
| 名称 | 人教版七年级下册数学 5.2.2平行线的判定 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 440.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 21:24:37 | ||
图片预览

文档简介
5. 2.2平行线的判定
基础闯关全练
1.如图.下列条件中能判定直线l?∥l?的是( )
∠1= ∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
1题图 2题图 3题图 4题图
2.如图,已知直线c与a、b分别交于点A、B,且∠1=120°,则当∠2=_________时,直线a//b( )
A.60° B.120° C.30° D.150°
3.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A.∠1= 70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
A.70° B.50° C.30° D.20°
4.如图,小明在两块含30°角的直角三角板的边缘画直线AB和CD,得到AB∥CD,这是根据______,两直线平行.
能力提升全练
1.如图,下列能判定AB∥EF的条件有( )
①∠B+∠BFE= 180°; ②∠1=∠2; ③∠3=∠4; ④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
1题图 2题图
2.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7= 180°;④∠5+∠8 =180°.其中能判定a∥b的条件是( )
①③ B.②④ C.①③④ D.①②③④
3.如图所示,∠1=65°,∠2=65°,∠3= 115°,试说明DE∥BC,DF∥AB.根据图形,完成下列推理:
因为∠1= 65°,∠2=65°,所以∠1=∠2.
所以______∥________( ).
因为AB,DE相交,所以∠1=∠4( ),
所以∠4= 65°.
因为∠3= 115°.
所以∠3+∠4= 180°,
所以______∥_______( ).
4.已知,如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2= 30°,∠1= 60°.求证:AB//CD.
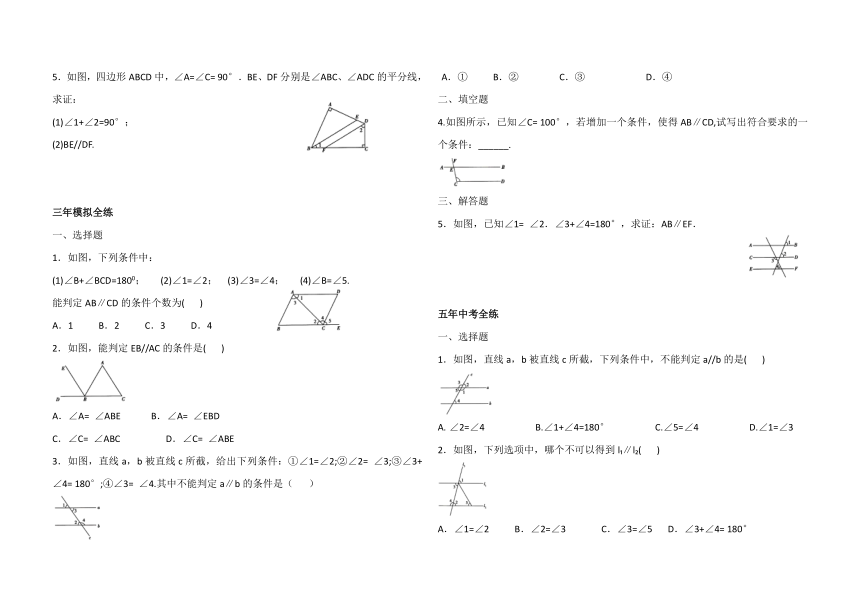
5.如图,四边形ABCD中,∠A=∠C= 90°.BE、DF分别是∠ABC、∠ADC的平分线,求证:
(1)∠1+∠2=90°;
(2)BE//DF.
三年模拟全练
一、选择题
1.如图,下列条件中:
(1)∠B+∠BCD=1800; (2)∠1=∠2; (3)∠3=∠4; (4)∠B=∠5.
能判定AB∥CD的条件个数为( )
A.1 B.2 C.3 D.4
2.如图,能判定EB//AC的条件是( )
∠A= ∠ABE B.∠A= ∠EBD
C.∠C= ∠ABC D.∠C= ∠ABE
3.如图,直线a,b被直线c所截,给出下列条件:①∠1=∠2;②∠2= ∠3;③∠3+∠4= 180°;④∠3= ∠4.其中不能判定a∥b的条件是( )
① B.② C.③ D.④
二、填空题
4.如图所示,已知∠C= 100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件:______.
三、解答题
5.如图,已知∠1= ∠2.∠3+∠4=180°,求证:AB∥EF.
五年中考全练
一、选择题
1.如图,直线a,b被直线c所截,下列条件中,不能判定a//b的是( )
∠2=∠4 B.∠1+∠4=180° C.∠5=∠4 D.∠1=∠3
2.如图,下列选项中,哪个不可以得到l?∥l?( )
∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4= 180°
3.如图,直线a、b被直线c所截,下列条件使a//b的是( )
∠1=∠6 B.∠2=∠6 C.∠1=∠3 D.∠5=∠7
4.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC= 150°,∠BCD= 30°,则( )
AB∥BC B.BC∥CD C.AB∥DC D.AB与CD相交
二、填空题
5.下图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是______________.
核心素养全练
1.如图,直线AB和CD被直线MN所截.
(1)如图①,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足_______时,AB//CD;
(2)如图②,EG平分∠MEB.FH平分∠DFE(平分的是一对同位角).则∠1与∠2满足______时,AB//CD;
(3)如图③,EG平分∠AEF.FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB//CD?为什么?
2.如图,已知∠B= 25°,∠BCD= 45°.∠CDE=30°,∠E=10°.试说明AB∥EF.
参考答案
1.C∠1和∠3是l?和l?被l?所截形成的同旁内角,若它们互补,则l?与l?平行,故C符合.
2.B如图,∠1=∠3=120°,根据同位角相等,两直线平行可知当∠2=∠3=120°时,a∥b.
3.D如图,∵b⊥c,∴∠2= 90°.∴∠1= 70°,∴要使a∥b,则直线b绕着点A顺时针旋转的度数可为90°-70°=20°.故选D.
4.答案 内错角相等
解析∵∠ABC=∠BCD=30°,∴AB∥CD(内错角相等,两直线平行).
1.C根据平行线的判定方法逐一进行判断.①∵∠B+∠BFE= 180°.∴AB∥EF,符合题意;②∵∠1=∠2.∴DE∥BC,不符合题意;③∵∠3=∠4.∴AB∥EF,符合题意;④∵∠B=∠5,∴AB∥EF,符合题意.故选C.
2.D∵∠1=∠2,∴a∥b(同位角相等,两直线平行),故①符合题意;∵∠3=∠6,∴a∥b(内错角相等,两直线平行),故②符合题意;∵∠4+∠7=180°.∠4=∠6,∴∠6+∠7= 180°,∴a∥b(同旁内角互补,两直线平行),故③符合题意;∵∠5+∠8= 180°, ∠5=∠3, ∠8=∠2.∴∠2+∠3= 180°,∴a∥b(同旁内角互补,两直线平行).故④符合题意.故选D.
3.答案DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
解析∠1与∠2是直线DE,BC被直线AB所截得到的同位角,所以DE∥BC,理由是“同位角相等,两直线平行”.∠1与∠4是两条直线AB与DE相交得到的对顶角,所以∠1=∠4,理由是“对顶角相等”.∠3与∠4是直线DF,AB被直线DE所截得到的同旁内角,所以DF∥AB,理由是“同旁内角互补,两直线平行”.
4.证明如图,∵GH⊥CD,(已知)
∴∠CHG= 90°.(垂直定义)
又∵∠2=30°,(已知)
∴∠3= 60°.∴∠4= 60°.(对顶角相等)
又∵∠1= 60°,(已知)
∴∠1=∠4.
∴AB∥CD(同位角相等,两直线平行).
5.证明(1)∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC= 180°,
∴2(∠1+∠2)= 180°,
∴∠1+∠2= 90°.
(2)在△FCD中,∵∠C= 90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE//DF.
一、选择题
1.C能判定AB∥CD的条件有(1)(3)(4),而由∠1-∠2只能得到AD∥BC.故选C.
2.AA项.∠A= ∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确;B项,由∠A= ∠EBD不能判定EB∥AC,故本选项错误;C项,由∠C= ∠ABC不能判定EB∥AC,故本选项错误;D项,由∠C= ∠ABE不能判定EB∥AC.故本选项错误.故选A.
3.D若∠1∠2,则a∥b(同位角相等,两直线平行);若∠2=∠3,则a∥b(内错角相等,两直线平行);若∠3+ ∠4= 180°,则a∥b(同旁内角互补,两直线平行);当∠3= ∠4时,不能判定a∥b.故选D.
二、填空题
4.答案答案不唯一,如∠BEC= 80°或∠AEC= 100°或∠FEB= 100°
三、解答题
5.证明∵∠1=∠2.∴AB∥CD,
∵∠3+∠4=180°.
∴CD //EF,
∴AB//EF.
一、选择题
1.D选项A符合同位角相等,两直线平行;选项B符合同旁内角互补,两直线平行;选项C符合内错角相等,两直线平行;只有选项D不能判定直线a与b平行.
2.C A项.∵∠1=∠2.∴l?∥l?(同位角相等,两直线平行);B项,∵∠2=∠3,∴l?∥l?(内错角相等,两直线平行);C项,由∠3=∠5不能判定l?∥l?;D项,∵∠3+∠4= 180°,∴l?∥l?(同旁内角互补,两直线平行).
3.B若∠2=∠6,则a∥b(同位角相等,两直线平行),故选B.
4.C∵∠ABC= 150°,∠BCD=30°,∴∠ABC+∠BCD= 180°,∴AB∥DC(同旁内角互补,两直线平行).故选C.
二、填空题
5.答案 同位角相等,两直线平行
解析由作平行线的过程可知,三角板移动前后的60°角为同位角,根据“同位角相等,两直线平行”的判定方法,可得过点P的直线与直线l平行.
1.解析(1) ∠1+∠2=90°.
(2)∠1=∠2.
(3)∠1=∠2.
理由:∵EG平分∠AEF,FH平分∠DFE,
∴ ∠AEF=2∠1,∠DFE=2∠2,
∵∠1=∠2,
∴∠AEF=∠DFE.
∴AB// CD.
2.证明如图,在∠BCD的内部作∠BCM=25°,在∠CDE的内部作∠EDN= 10°.
因为∠B=25°,∠E=10°.
所以∠B=∠BCM,∠E=∠EDN,
所以AB//CM,EF//ND.
又因为∠BCD=45°,∠CDE=30°,
所以∠DCM=20°,∠CDN=20°,
所以∠DCM=∠CDN.
所以CM//ND,所以AB//EF.
基础闯关全练
1.如图.下列条件中能判定直线l?∥l?的是( )
∠1= ∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
1题图 2题图 3题图 4题图
2.如图,已知直线c与a、b分别交于点A、B,且∠1=120°,则当∠2=_________时,直线a//b( )
A.60° B.120° C.30° D.150°
3.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A.∠1= 70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
A.70° B.50° C.30° D.20°
4.如图,小明在两块含30°角的直角三角板的边缘画直线AB和CD,得到AB∥CD,这是根据______,两直线平行.
能力提升全练
1.如图,下列能判定AB∥EF的条件有( )
①∠B+∠BFE= 180°; ②∠1=∠2; ③∠3=∠4; ④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
1题图 2题图
2.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7= 180°;④∠5+∠8 =180°.其中能判定a∥b的条件是( )
①③ B.②④ C.①③④ D.①②③④
3.如图所示,∠1=65°,∠2=65°,∠3= 115°,试说明DE∥BC,DF∥AB.根据图形,完成下列推理:
因为∠1= 65°,∠2=65°,所以∠1=∠2.
所以______∥________( ).
因为AB,DE相交,所以∠1=∠4( ),
所以∠4= 65°.
因为∠3= 115°.
所以∠3+∠4= 180°,
所以______∥_______( ).
4.已知,如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2= 30°,∠1= 60°.求证:AB//CD.
5.如图,四边形ABCD中,∠A=∠C= 90°.BE、DF分别是∠ABC、∠ADC的平分线,求证:
(1)∠1+∠2=90°;
(2)BE//DF.
三年模拟全练
一、选择题
1.如图,下列条件中:
(1)∠B+∠BCD=1800; (2)∠1=∠2; (3)∠3=∠4; (4)∠B=∠5.
能判定AB∥CD的条件个数为( )
A.1 B.2 C.3 D.4
2.如图,能判定EB//AC的条件是( )
∠A= ∠ABE B.∠A= ∠EBD
C.∠C= ∠ABC D.∠C= ∠ABE
3.如图,直线a,b被直线c所截,给出下列条件:①∠1=∠2;②∠2= ∠3;③∠3+∠4= 180°;④∠3= ∠4.其中不能判定a∥b的条件是( )
① B.② C.③ D.④
二、填空题
4.如图所示,已知∠C= 100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件:______.
三、解答题
5.如图,已知∠1= ∠2.∠3+∠4=180°,求证:AB∥EF.
五年中考全练
一、选择题
1.如图,直线a,b被直线c所截,下列条件中,不能判定a//b的是( )
∠2=∠4 B.∠1+∠4=180° C.∠5=∠4 D.∠1=∠3
2.如图,下列选项中,哪个不可以得到l?∥l?( )
∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4= 180°
3.如图,直线a、b被直线c所截,下列条件使a//b的是( )
∠1=∠6 B.∠2=∠6 C.∠1=∠3 D.∠5=∠7
4.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC= 150°,∠BCD= 30°,则( )
AB∥BC B.BC∥CD C.AB∥DC D.AB与CD相交
二、填空题
5.下图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是______________.
核心素养全练
1.如图,直线AB和CD被直线MN所截.
(1)如图①,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足_______时,AB//CD;
(2)如图②,EG平分∠MEB.FH平分∠DFE(平分的是一对同位角).则∠1与∠2满足______时,AB//CD;
(3)如图③,EG平分∠AEF.FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB//CD?为什么?
2.如图,已知∠B= 25°,∠BCD= 45°.∠CDE=30°,∠E=10°.试说明AB∥EF.
参考答案
1.C∠1和∠3是l?和l?被l?所截形成的同旁内角,若它们互补,则l?与l?平行,故C符合.
2.B如图,∠1=∠3=120°,根据同位角相等,两直线平行可知当∠2=∠3=120°时,a∥b.
3.D如图,∵b⊥c,∴∠2= 90°.∴∠1= 70°,∴要使a∥b,则直线b绕着点A顺时针旋转的度数可为90°-70°=20°.故选D.
4.答案 内错角相等
解析∵∠ABC=∠BCD=30°,∴AB∥CD(内错角相等,两直线平行).
1.C根据平行线的判定方法逐一进行判断.①∵∠B+∠BFE= 180°.∴AB∥EF,符合题意;②∵∠1=∠2.∴DE∥BC,不符合题意;③∵∠3=∠4.∴AB∥EF,符合题意;④∵∠B=∠5,∴AB∥EF,符合题意.故选C.
2.D∵∠1=∠2,∴a∥b(同位角相等,两直线平行),故①符合题意;∵∠3=∠6,∴a∥b(内错角相等,两直线平行),故②符合题意;∵∠4+∠7=180°.∠4=∠6,∴∠6+∠7= 180°,∴a∥b(同旁内角互补,两直线平行),故③符合题意;∵∠5+∠8= 180°, ∠5=∠3, ∠8=∠2.∴∠2+∠3= 180°,∴a∥b(同旁内角互补,两直线平行).故④符合题意.故选D.
3.答案DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
解析∠1与∠2是直线DE,BC被直线AB所截得到的同位角,所以DE∥BC,理由是“同位角相等,两直线平行”.∠1与∠4是两条直线AB与DE相交得到的对顶角,所以∠1=∠4,理由是“对顶角相等”.∠3与∠4是直线DF,AB被直线DE所截得到的同旁内角,所以DF∥AB,理由是“同旁内角互补,两直线平行”.
4.证明如图,∵GH⊥CD,(已知)
∴∠CHG= 90°.(垂直定义)
又∵∠2=30°,(已知)
∴∠3= 60°.∴∠4= 60°.(对顶角相等)
又∵∠1= 60°,(已知)
∴∠1=∠4.
∴AB∥CD(同位角相等,两直线平行).
5.证明(1)∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC= 180°,
∴2(∠1+∠2)= 180°,
∴∠1+∠2= 90°.
(2)在△FCD中,∵∠C= 90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE//DF.
一、选择题
1.C能判定AB∥CD的条件有(1)(3)(4),而由∠1-∠2只能得到AD∥BC.故选C.
2.AA项.∠A= ∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确;B项,由∠A= ∠EBD不能判定EB∥AC,故本选项错误;C项,由∠C= ∠ABC不能判定EB∥AC,故本选项错误;D项,由∠C= ∠ABE不能判定EB∥AC.故本选项错误.故选A.
3.D若∠1∠2,则a∥b(同位角相等,两直线平行);若∠2=∠3,则a∥b(内错角相等,两直线平行);若∠3+ ∠4= 180°,则a∥b(同旁内角互补,两直线平行);当∠3= ∠4时,不能判定a∥b.故选D.
二、填空题
4.答案答案不唯一,如∠BEC= 80°或∠AEC= 100°或∠FEB= 100°
三、解答题
5.证明∵∠1=∠2.∴AB∥CD,
∵∠3+∠4=180°.
∴CD //EF,
∴AB//EF.
一、选择题
1.D选项A符合同位角相等,两直线平行;选项B符合同旁内角互补,两直线平行;选项C符合内错角相等,两直线平行;只有选项D不能判定直线a与b平行.
2.C A项.∵∠1=∠2.∴l?∥l?(同位角相等,两直线平行);B项,∵∠2=∠3,∴l?∥l?(内错角相等,两直线平行);C项,由∠3=∠5不能判定l?∥l?;D项,∵∠3+∠4= 180°,∴l?∥l?(同旁内角互补,两直线平行).
3.B若∠2=∠6,则a∥b(同位角相等,两直线平行),故选B.
4.C∵∠ABC= 150°,∠BCD=30°,∴∠ABC+∠BCD= 180°,∴AB∥DC(同旁内角互补,两直线平行).故选C.
二、填空题
5.答案 同位角相等,两直线平行
解析由作平行线的过程可知,三角板移动前后的60°角为同位角,根据“同位角相等,两直线平行”的判定方法,可得过点P的直线与直线l平行.
1.解析(1) ∠1+∠2=90°.
(2)∠1=∠2.
(3)∠1=∠2.
理由:∵EG平分∠AEF,FH平分∠DFE,
∴ ∠AEF=2∠1,∠DFE=2∠2,
∵∠1=∠2,
∴∠AEF=∠DFE.
∴AB// CD.
2.证明如图,在∠BCD的内部作∠BCM=25°,在∠CDE的内部作∠EDN= 10°.
因为∠B=25°,∠E=10°.
所以∠B=∠BCM,∠E=∠EDN,
所以AB//CM,EF//ND.
又因为∠BCD=45°,∠CDE=30°,
所以∠DCM=20°,∠CDN=20°,
所以∠DCM=∠CDN.
所以CM//ND,所以AB//EF.
