六年级上册数学单元测试-数学好玩 北师大版(含解析)
文档属性
| 名称 | 六年级上册数学单元测试-数学好玩 北师大版(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 80.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-03 00:00:00 | ||
图片预览


文档简介
六年级上册数学单元测试-数学好玩
一、单选题
1.将8支球队分成两个小组,各小组采用单循环制;小组前2名共4支球队再进行淘汰制,决出冠军和亚军,一共需要赛????? 场.(??? )
A.?28场?????????????????????????????????????B.?7场?????????????????????????????????????C.?35场?????????????????????????????????????D.?15场
2.小明、小英、小华一起照相,他们的位置有( )种不同的排列方法.
A.?6?????????????????????????????????????????????B.?10?????????????????????????????????????????????C.?3
3.数一数如图中有( )条线段.
A.?1条??????????????????????????????????????B.?4条??????????????????????????????????????C.?9条??????????????????????????????????????D.?10条
4.由数字0、1、2、3可以组成(??? )个没有重复数字的偶数。
A.?18?????????????????????????????????????????B.?36?????????????????????????????????????????C.?27?????????????????????????????????????????D.?48
二、判断题
5.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法(??? )
6.有三个同学,每两人握一次手,一共要握6次手。( ??)
7.…第25个应该是 。(?? )
三、填空题
8.看图填数.? ________??-? 5=________
9.我当裁判.
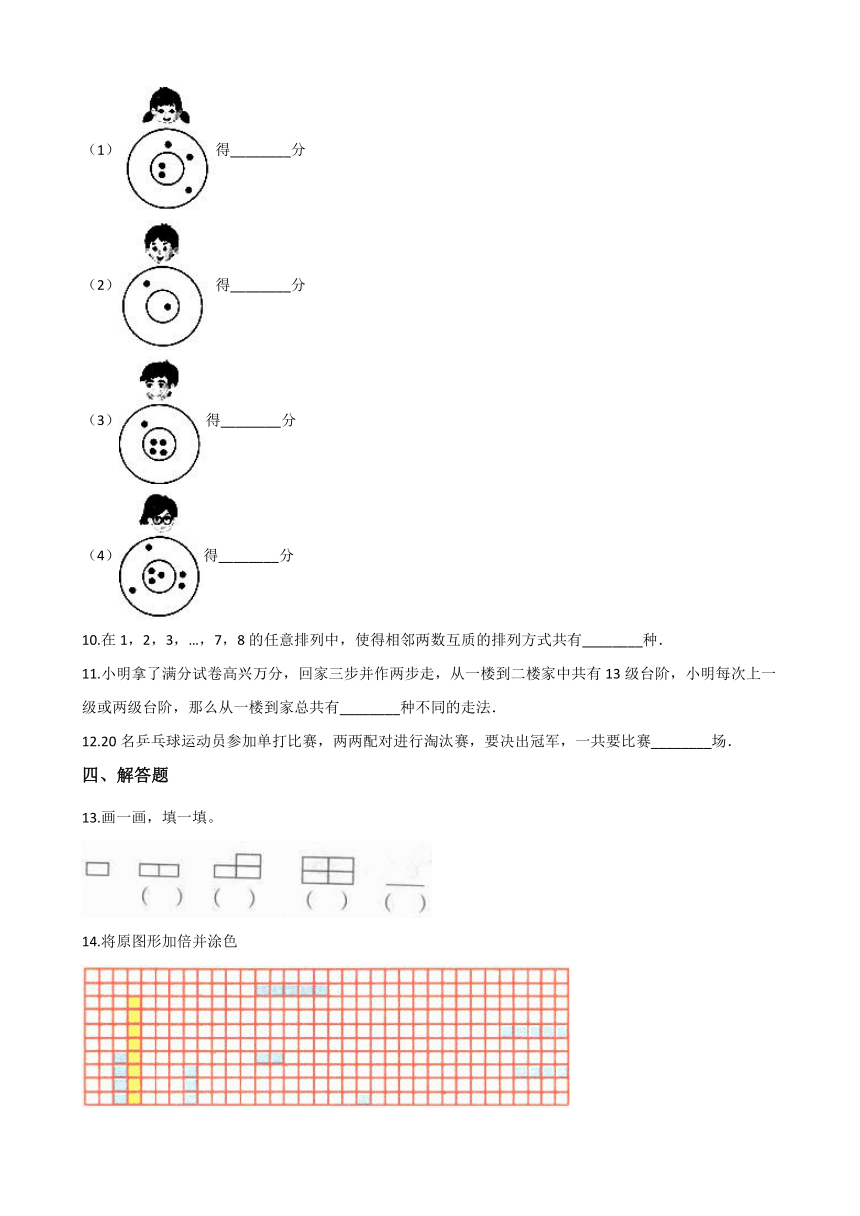
游园会上,小伙伴们玩投飞镖游戏,投中圈内的10分,投在圈外的1分,他们各得了多少分?
?
(1)得________分
(2)得________分
(3)得________分
(4)得________分
10.在1,2,3,…,7,8的任意排列中,使得相邻两数互质的排列方式共有________种.
11.小明拿了满分试卷高兴万分,回家三步并作两步走,从一楼到二楼家中共有13级台阶,小明每次上一级或两级台阶,那么从一楼到家总共有________种不同的走法.
12.20名乒乓球运动员参加单打比赛,两两配对进行淘汰赛,要决出冠军,一共要比赛________场.
四、解答题
13.画一画,填一填。
14.将原图形加倍并涂色
五、综合题
15.某校三年级同学租车去游园,每班去32人,有12个班 。
(1)三年级一共有多少人参加游园?
(2)租7辆客车够不够?
六、应用题
16.在1~20共20个整数中,取两个数相加,使其和为偶数不同取法共有多少种?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:单循环赛:8÷2=4(支) 3+2+1=6(场) 6×2=12(场) 淘汰赛:4÷2=2(场) 2÷2=1(场) 12+3=15(场) 故答案为:15.
【分析】用8除以2求出每组球队的支数,再求出每组进行单循环赛的场次,然后乘2求出单循环赛的场次;因为淘汰赛每场都要淘汰一半的球队,所以直接用球队的支数依次除以2求出淘汰赛的场次,再加上单循环赛的场次即可。
2.【答案】 A
【解析】【解答】解:3×2×1=6(种)
答:他们的位置有6种不同的排列方法.
故选:A.
【分析】首先根据题意,判断出排在第一的有3种排法,排在第二的有2种排法,排在第三的有1种排法;然后根据乘法原理,求出他们的位置有多少种不同的排列方法即可.
3.【答案】 D
【解析】【解答】解:根据题意,这条线上的5个点,它的组合情况是:
5×4÷2=20÷2=10(条);
答:图中一共有10条线段.
故选:D.
【分析】这条线上一共有5个点,每两个点都可以组成一条线段,一共有5×4种排列情况,又由于每两个点都重复了一次,比如AB和BA就是同一条线段,所以这条线上的5个点,一共有5×4÷2种组合.
4.【答案】 C
【解析】【解答】解:四位数:①个位为0时,千位数字是1、2、3中选一个,有3种选法,百位就是1、2、3中剩下的2个数选1,是2种选择,十位只有1种选择,所以有:3×2=6(个);②个位为2时,千位数字是1、3两种选择,百位是0、1、3中剩下的2个数字可以选择,十位只有1种选择,共2×2=4(种); 三位数:120、210、130、310、320、230、132、312、102、302共10个; 两位数:10、20、30、12、32共5个; 一位数:0、2共2个; 所以一共有:6+4+10+5+2=27(个)。 故答案为:C。
【分析】组成的数字可以是一位数、两位数、三位数、四位数,因为是偶数,所以个位数字一定是0或2,这样经过计算或者列举出所有的数字即可。
二、判断题
5.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。 故答案为:正确。 【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
6.【答案】 错误
【解析】【解答】 3×2÷2=3(次) 故答案为:错误。 【分析】握手的次数=人数×(人数-1)÷2。
7.【答案】正确
【解析】
三、填空题
8.【答案】15;10
【解析】
9.【答案】(1)23 (2)11 (3)41 (4)34
【解析】
10.【答案】1728
【解析】【解答】解:这8个数之间如果有公因数,那么无非是2或3. 8个数中的4个偶数一定不能相邻,考虑使用“插入法”, 即首先忽略偶数的存在,对奇数进行排列,然后将偶数插入,但在偶数插入时,还要考虑3和6相邻的情况. 奇数的排列一共有:4!=24(种), 对任意一种排列4个数形成5个空位,将6插入,可以有符合条件的3个位置可以插,再在剩下的四个位置中插入2、4、8,一共有4×3×2=24(种), 综上所述,一共有:24×3×24=1728(种). 答:使得相邻两数互质的排列方式共有 1728种. 故答案为:1728. 【分析】这8个数之间如果有公因数,那么无非是2或3. 8个数中的4个偶数一定不能相邻,对于这类多个元素不相邻的排列问题,考虑使用“插入法”,即首先忽略偶数的存在,对奇数进行排列,然后将偶数插入,但在偶数插入时,还要考虑3和6相邻的情况. 奇数的排列一共有4!=24种,对任意一种排列4个数形成5个空位,将6插入,可以有符合条件的3个位置可以插,再在剩下的四个位置中插入2、4、8,一共有4×3×2=24种,一共有24×3×24=1728种.
11.【答案】 377
【解析】【解答】解: 根据题意列出各级楼梯的走法如下:括号里面的数字表示每次上楼梯走的级数,1个算式或数表示一种走法: 第一级:1种(1) 第二级:2种(1+1,2) 第三级:3种(1+1+1,2+1,1+2) 第四级:5种(1+1+1+1,1+1+2,1+2+1,2+1+1,2+2) 第五级:8种(1+1+1+1+1,1+1+1+2,1+1+2+1,1+2+1+1,2+1+1+1,1+2+2,2+1+2,2+2+1) 第六级:… 其规律为:从第三项起,每一项的数都是紧挨着它前面的两项的数字之和。 1、2、3、5、8、13、21、34、55、89、144、233,377。 从一楼到家一共有377种不同的走法。 故答案为:377。 【分析】根据每级台阶的不同走法判断出每级走的种类之间的规律,然后确定13级台阶的走法种类即可。
12.【答案】19
【解析】【解答】解:10+5+2+1+1=19(场) 故答案为:19 【分析】第一轮10场淘汰10人;第二轮5场淘汰5人;第三轮两两比赛2场淘汰2人,剩下3人;第三轮两两比赛1场淘汰1人;最后一轮比赛1场.
四、解答题
13.【答案】
【解析】
14.【答案】解:
【解析】
五、综合题
15.【答案】(1)解:32×12=384(人)
答:三年级一共有384人参加游园。
(2)解:54×7=378(人)
378<384
答:租7辆客车不够。
【解析】【分析】(1)根据题目中给出的每个班去的人数和班级数求出一共参加游园的人数; (2)根据题目中图片上的条件和所租车辆数求出一共可以坐的人数,然后与去的人数进行比较得到结果。
六、应用题
16.【答案】90种
【解析】【解答】9×10÷2×2=90(种) 答:和为偶数不同取法共有90种。 【分析】从1~20种共有10个偶数,10个奇数,如果偶数与偶数相加,则有9×10÷2=45种,同样奇数与奇数相加也有45种不同的取法,所以再用45乘2即可求出一共的取法。
一、单选题
1.将8支球队分成两个小组,各小组采用单循环制;小组前2名共4支球队再进行淘汰制,决出冠军和亚军,一共需要赛????? 场.(??? )
A.?28场?????????????????????????????????????B.?7场?????????????????????????????????????C.?35场?????????????????????????????????????D.?15场
2.小明、小英、小华一起照相,他们的位置有( )种不同的排列方法.
A.?6?????????????????????????????????????????????B.?10?????????????????????????????????????????????C.?3
3.数一数如图中有( )条线段.
A.?1条??????????????????????????????????????B.?4条??????????????????????????????????????C.?9条??????????????????????????????????????D.?10条
4.由数字0、1、2、3可以组成(??? )个没有重复数字的偶数。
A.?18?????????????????????????????????????????B.?36?????????????????????????????????????????C.?27?????????????????????????????????????????D.?48
二、判断题
5.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法(??? )
6.有三个同学,每两人握一次手,一共要握6次手。( ??)
7.…第25个应该是 。(?? )
三、填空题
8.看图填数.? ________??-? 5=________
9.我当裁判.
游园会上,小伙伴们玩投飞镖游戏,投中圈内的10分,投在圈外的1分,他们各得了多少分?
?
(1)得________分
(2)得________分
(3)得________分
(4)得________分
10.在1,2,3,…,7,8的任意排列中,使得相邻两数互质的排列方式共有________种.
11.小明拿了满分试卷高兴万分,回家三步并作两步走,从一楼到二楼家中共有13级台阶,小明每次上一级或两级台阶,那么从一楼到家总共有________种不同的走法.
12.20名乒乓球运动员参加单打比赛,两两配对进行淘汰赛,要决出冠军,一共要比赛________场.
四、解答题
13.画一画,填一填。
14.将原图形加倍并涂色
五、综合题
15.某校三年级同学租车去游园,每班去32人,有12个班 。
(1)三年级一共有多少人参加游园?
(2)租7辆客车够不够?
六、应用题
16.在1~20共20个整数中,取两个数相加,使其和为偶数不同取法共有多少种?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:单循环赛:8÷2=4(支) 3+2+1=6(场) 6×2=12(场) 淘汰赛:4÷2=2(场) 2÷2=1(场) 12+3=15(场) 故答案为:15.
【分析】用8除以2求出每组球队的支数,再求出每组进行单循环赛的场次,然后乘2求出单循环赛的场次;因为淘汰赛每场都要淘汰一半的球队,所以直接用球队的支数依次除以2求出淘汰赛的场次,再加上单循环赛的场次即可。
2.【答案】 A
【解析】【解答】解:3×2×1=6(种)
答:他们的位置有6种不同的排列方法.
故选:A.
【分析】首先根据题意,判断出排在第一的有3种排法,排在第二的有2种排法,排在第三的有1种排法;然后根据乘法原理,求出他们的位置有多少种不同的排列方法即可.
3.【答案】 D
【解析】【解答】解:根据题意,这条线上的5个点,它的组合情况是:
5×4÷2=20÷2=10(条);
答:图中一共有10条线段.
故选:D.
【分析】这条线上一共有5个点,每两个点都可以组成一条线段,一共有5×4种排列情况,又由于每两个点都重复了一次,比如AB和BA就是同一条线段,所以这条线上的5个点,一共有5×4÷2种组合.
4.【答案】 C
【解析】【解答】解:四位数:①个位为0时,千位数字是1、2、3中选一个,有3种选法,百位就是1、2、3中剩下的2个数选1,是2种选择,十位只有1种选择,所以有:3×2=6(个);②个位为2时,千位数字是1、3两种选择,百位是0、1、3中剩下的2个数字可以选择,十位只有1种选择,共2×2=4(种); 三位数:120、210、130、310、320、230、132、312、102、302共10个; 两位数:10、20、30、12、32共5个; 一位数:0、2共2个; 所以一共有:6+4+10+5+2=27(个)。 故答案为:C。
【分析】组成的数字可以是一位数、两位数、三位数、四位数,因为是偶数,所以个位数字一定是0或2,这样经过计算或者列举出所有的数字即可。
二、判断题
5.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。 故答案为:正确。 【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
6.【答案】 错误
【解析】【解答】 3×2÷2=3(次) 故答案为:错误。 【分析】握手的次数=人数×(人数-1)÷2。
7.【答案】正确
【解析】
三、填空题
8.【答案】15;10
【解析】
9.【答案】(1)23 (2)11 (3)41 (4)34
【解析】
10.【答案】1728
【解析】【解答】解:这8个数之间如果有公因数,那么无非是2或3. 8个数中的4个偶数一定不能相邻,考虑使用“插入法”, 即首先忽略偶数的存在,对奇数进行排列,然后将偶数插入,但在偶数插入时,还要考虑3和6相邻的情况. 奇数的排列一共有:4!=24(种), 对任意一种排列4个数形成5个空位,将6插入,可以有符合条件的3个位置可以插,再在剩下的四个位置中插入2、4、8,一共有4×3×2=24(种), 综上所述,一共有:24×3×24=1728(种). 答:使得相邻两数互质的排列方式共有 1728种. 故答案为:1728. 【分析】这8个数之间如果有公因数,那么无非是2或3. 8个数中的4个偶数一定不能相邻,对于这类多个元素不相邻的排列问题,考虑使用“插入法”,即首先忽略偶数的存在,对奇数进行排列,然后将偶数插入,但在偶数插入时,还要考虑3和6相邻的情况. 奇数的排列一共有4!=24种,对任意一种排列4个数形成5个空位,将6插入,可以有符合条件的3个位置可以插,再在剩下的四个位置中插入2、4、8,一共有4×3×2=24种,一共有24×3×24=1728种.
11.【答案】 377
【解析】【解答】解: 根据题意列出各级楼梯的走法如下:括号里面的数字表示每次上楼梯走的级数,1个算式或数表示一种走法: 第一级:1种(1) 第二级:2种(1+1,2) 第三级:3种(1+1+1,2+1,1+2) 第四级:5种(1+1+1+1,1+1+2,1+2+1,2+1+1,2+2) 第五级:8种(1+1+1+1+1,1+1+1+2,1+1+2+1,1+2+1+1,2+1+1+1,1+2+2,2+1+2,2+2+1) 第六级:… 其规律为:从第三项起,每一项的数都是紧挨着它前面的两项的数字之和。 1、2、3、5、8、13、21、34、55、89、144、233,377。 从一楼到家一共有377种不同的走法。 故答案为:377。 【分析】根据每级台阶的不同走法判断出每级走的种类之间的规律,然后确定13级台阶的走法种类即可。
12.【答案】19
【解析】【解答】解:10+5+2+1+1=19(场) 故答案为:19 【分析】第一轮10场淘汰10人;第二轮5场淘汰5人;第三轮两两比赛2场淘汰2人,剩下3人;第三轮两两比赛1场淘汰1人;最后一轮比赛1场.
四、解答题
13.【答案】
【解析】
14.【答案】解:
【解析】
五、综合题
15.【答案】(1)解:32×12=384(人)
答:三年级一共有384人参加游园。
(2)解:54×7=378(人)
378<384
答:租7辆客车不够。
【解析】【分析】(1)根据题目中给出的每个班去的人数和班级数求出一共参加游园的人数; (2)根据题目中图片上的条件和所租车辆数求出一共可以坐的人数,然后与去的人数进行比较得到结果。
六、应用题
16.【答案】90种
【解析】【解答】9×10÷2×2=90(种) 答:和为偶数不同取法共有90种。 【分析】从1~20种共有10个偶数,10个奇数,如果偶数与偶数相加,则有9×10÷2=45种,同样奇数与奇数相加也有45种不同的取法,所以再用45乘2即可求出一共的取法。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
