五年级上册数学一课一练-6.4组合图形的面积 人教版(含解析)
文档属性
| 名称 | 五年级上册数学一课一练-6.4组合图形的面积 人教版(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 158.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-03 13:57:47 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学一课一练-6.4组合图形的面积
一、单选题
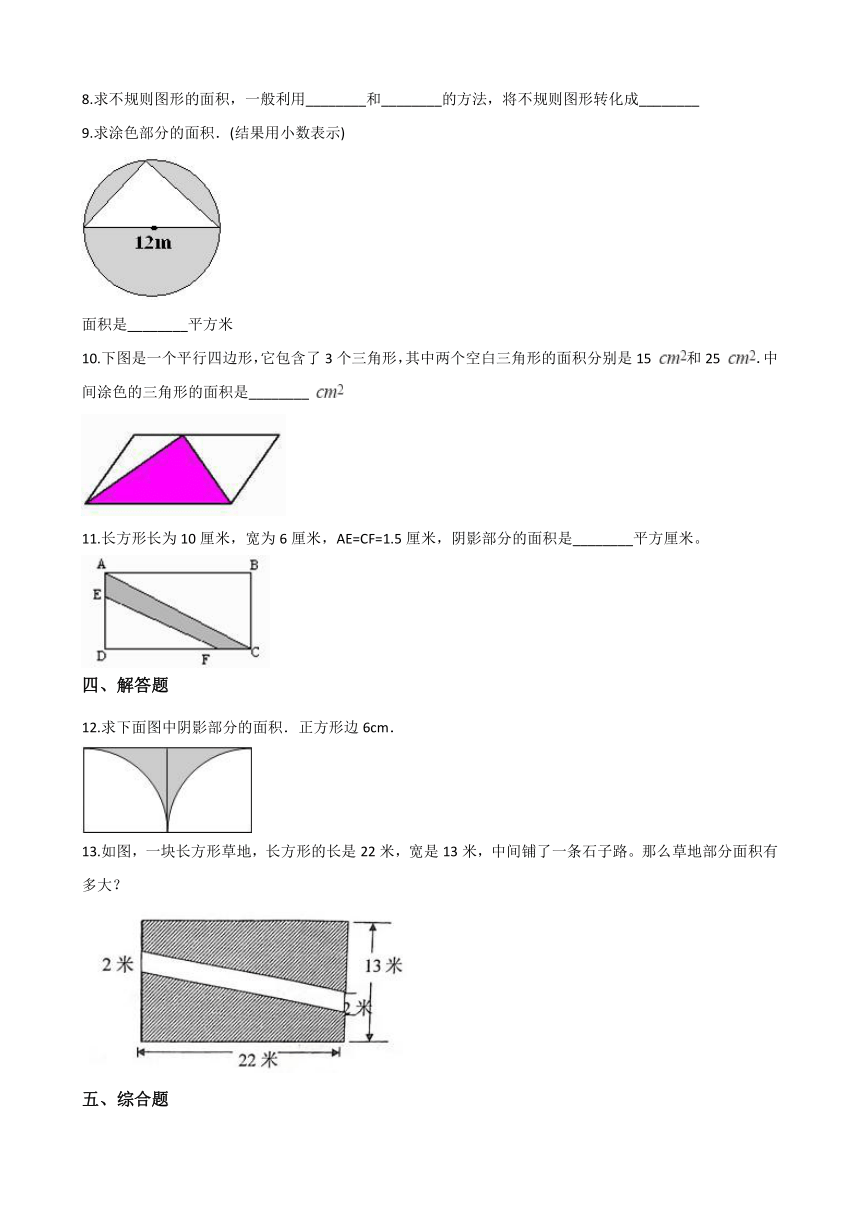
1.如下图,在一片梯形草坪中间开了一条宽3米的平行四边形小路,草坪的面积是(
)平方米。
A. 300 B. 255 C. 345 D. 45
2.一个梯形的上底增加3厘米,下底减少3厘米,要使梯形的面积不变,高(
)。
A. 变小了 B. 不变 C. 变大了
3.图中阴影部分的面积是3平方厘米.那么圆环的面积是(
)平方厘米。
A. 9.42 B. 9 C. 18.84 D. 无法知道
二、判断题
4.计算组合图形的面积也要用到基本图形的面积公式。
5.左图中,A图与B图的周长不相等,面积也不相等。
6.下面两图中阴影部分的面积相等。(每个小方格的边长表示1cm)
三、填空题
7.下图阴影部分的面积是________平方厘米(用小数表示)(单位:厘米)
8.求不规则图形的面积,一般利用________和________的方法,将不规则图形转化成________
9.求涂色部分的面积.(结果用小数表示)
面积是________平方米
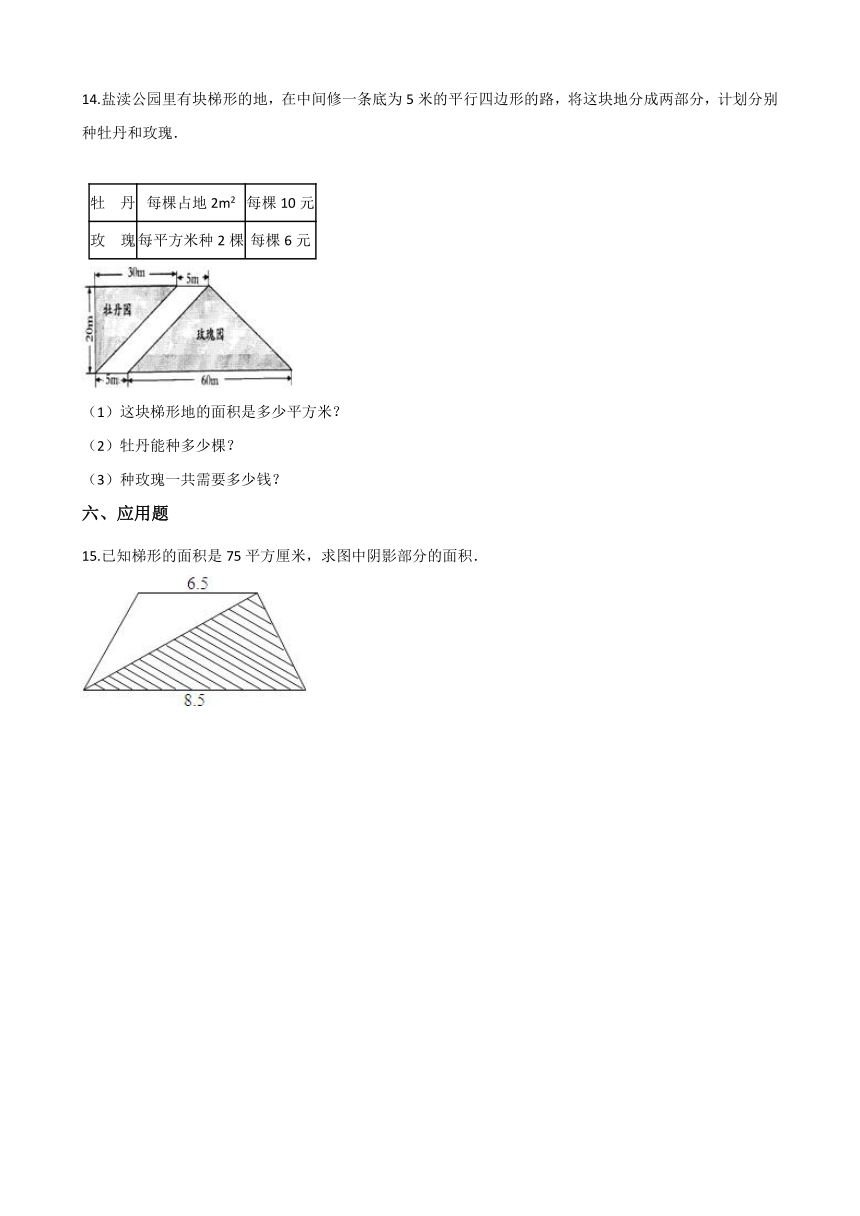
10.下图是一个平行四边形,它包含了3个三角形,其中两个空白三角形的面积分别是15
和25
.中间涂色的三角形的面积是________
11.长方形长为10厘米,宽为6厘米,AE=CF=1.5厘米,阴影部分的面积是________平方厘米。
四、解答题
12.求下面图中阴影部分的面积.正方形边6cm.
13.如图,一块长方形草地,长方形的长是22米,宽是13米,中间铺了一条石子路。那么草地部分面积有多大?
五、综合题
14.盐渎公园里有块梯形的地,在中间修一条底为5米的平行四边形的路,将这块地分成两部分,计划分别种牡丹和玫瑰.
牡 丹
每棵占地2m2
每棵10元
玫 瑰
每平方米种2棵
每棵6元
(1)这块梯形地的面积是多少平方米?
(2)牡丹能种多少棵?
(3)种玫瑰一共需要多少钱?
六、应用题
15.已知梯形的面积是75平方厘米,求图中阴影部分的面积.
参考答案
一、单选题
1.【答案】
B
【解析】【解答】解:(14+26)×15÷2-3×15=255(平方米)
故答案为:B。
【分析】先计算梯形的面积,再计算平行四边形的面积,用梯形面积减去平行四边形的面积即可。
2.【答案】B
【解析】【解答】因为梯形的面积=(上底+下底)×高÷2,“上底增加3厘米,下底减少3厘米,面积不变”则(上底+下底)的和不变,且面积不变,所以梯形的高不变。
故选:B
【分析】梯形的面积=(上底+下底)×高÷2,若“上底增加3米,下底减少3米,面积不变”则(上底+下底)的和不变,且面积不变,从而得知梯形的高也不变。
3.【答案】C
【解析】【解答】解:设外圆半径是R厘米,内圆半径是r厘米,
R×R÷2-r×r÷2=3
R -r =6
圆环面积:S=π×(R -r )=3.14×6=18.84(平方厘米)
故答案为:C
【分析】外圆半径就是大三角形的直角边长,内圆半径就是小三角形的直角边长;根据阴影部分的面积是3平方厘米计算出外圆半径的平方与内圆半径的平方的差,然后根据圆环面积公式计算面积即可.
二、判断题
4.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。
故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
5.【答案】错误
【解析】【解答】A图与B图的周长相等,面积不相等,原题说法错误.
故答案为:错误.
【分析】根据题意,A图的周长包括一条长和一条宽的长度之和及中间曲线的长度,B图的周长也包括一条长和一条宽的长度之和及中间曲线的长度,长方形的对边相等,所以周长相等,图形B的面积大于图形A的面积,据此解答.
6.【答案】正确
【解析】【解答】根据分析,作图如下:
(1)2×2÷2×2
=4÷2×2
=4(cm2)
(2)2×1+2×2÷2
=2+4÷2
=2+2
=4(cm2)
两图中阴影部分的面积相等,原题说法正确.
故答案为:正确.【分析】(1)第一个图的阴影部分可以分成两个底为2厘米,高为2厘米的相等三角形,据此利用三角形的面积公式计算即可;(2)第二个图的阴影部分可以分成一个长为2厘米,宽为1厘米的长方形与一个底是2厘米,高是2厘米的三角形,将两个图形的面积相加即可得到阴影部分的面积,然后比较两个图的阴影部分的面积大小即可.
三、填空题
7.【答案】533.8
【解析】【解答】7+24+13=44(厘米)
3.14×(44÷2) ÷2-3.14×(24÷2) ÷2
=3.14×484÷2-3.14×144÷2
=759.88-226.08
=533.8(平方厘米)
故答案为:533.8
【分析】阴影部分的面积是大半圆的面积减去空白部分小半圆的面积,先计算大半圆的直径,然后根据圆面积公式计算.
8.【答案】平移;旋转;规则图形
【解析】【解答】解:求不规则图形的面积,一般利用平移和旋转的方法,将不规则图形转化成规则图形.
故答案为:平移;旋转;规则图形【分析】由于不规则图形无法直接计算面积,所以要把不规则图形转化成规则图形来计算面积,这种方法叫作转化法.
9.【答案】
77.04
【解析】【解答】解:12÷2=6(米),
3.14×6 -12×6÷2
=113.04-36
=77.04(平方米)
故答案为:77.04
【分析】用圆面积减去空白部分三角形的面积就是涂色部分的面积。空白部分三角形的高就是圆的半径,由此计算即可。
10.【答案】40
【解析】
11.【答案】10.875
【解析】【解答】解:10×6÷2-(10-1.5)×(6-1.5)÷2
=30-8.5×4.5÷2
=30-38.25÷2
=30-19.125
=10.875
答:阴影面积是10.875
大三角形的面积减去小三角形的面积.
【分析】阴影部分的面积是两个三角形面积的差
四、解答题
12.【答案】解:(6×
)×2
=
=(36﹣28.26)×2
=7.74×2
=15.48(平方厘米),
答:阴影部分的面积是15.48平方厘米
【解析】【分析】首先用正方形的面积减去半径为6厘米的圆面积的
求出阴影部分面积的一半,然后再乘2即可.根据正方形的面积公式:s=a2
,
圆的面积公式:s=πr2
,
把数据代入公式解答.此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式.
13.【答案】
解:22×13-2×22=242(平方米)
答:草地部分面积242平方米。
【解析】【分析】草地部分面积=大长方形的面积-石子路的面积,其中长方形的面积=长×宽,从图中看出,石子路是一个平行四边形,它的高是长方形的长,所以石子路的面积=底×高,据此代入数据作答即可。
五、综合题
14.【答案】(1)解:牡丹园面积:
30×20÷2
=600÷2
=300(平方米)
玫瑰园的面积:
60×20÷2
=1200÷2
=600(平方米)
路的面积;
5×20=100(平方米)
总面积:
300+600+100=1000(平方米)
答:这块梯形地的面积是1000平方米
(2)解:300÷2=150(棵)
答:牡丹能种150棵.
(3)解:600×2×6
=1200×6
=7200(元)
答:种玫瑰一共需要7200元
【解析】【分析】(1)根据三角形的面积公式分别求出牡丹园、玫瑰园的面积,再加上路的面积;再求三者之和即可.(2)用牡丹园的面积除以每棵占地面积,即为能种多少棵牡丹.(3)用玫瑰园的面积乘以2,即为种玫瑰的棵数,再乘以玫瑰的单价,即为种玫瑰一共需要多少钱.
六、应用题
15.【答案】解:8.5×[75×2÷(8.5+6.5)]÷2,
=8.5×10÷2,
=42.5(平方厘米);
答:阴影部分的面积是42.5平方厘米
【解析】【分析】我们用梯形的面积乘以2除以上下底的和就是梯形的高,然后运用三角形的面积公式求出阴影部分的面积.本题运用梯形的面积公式及三角形的面积公式进行解答即可.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学一课一练-6.4组合图形的面积
一、单选题
1.如下图,在一片梯形草坪中间开了一条宽3米的平行四边形小路,草坪的面积是(
)平方米。
A. 300 B. 255 C. 345 D. 45
2.一个梯形的上底增加3厘米,下底减少3厘米,要使梯形的面积不变,高(
)。
A. 变小了 B. 不变 C. 变大了
3.图中阴影部分的面积是3平方厘米.那么圆环的面积是(
)平方厘米。
A. 9.42 B. 9 C. 18.84 D. 无法知道
二、判断题
4.计算组合图形的面积也要用到基本图形的面积公式。
5.左图中,A图与B图的周长不相等,面积也不相等。
6.下面两图中阴影部分的面积相等。(每个小方格的边长表示1cm)
三、填空题
7.下图阴影部分的面积是________平方厘米(用小数表示)(单位:厘米)
8.求不规则图形的面积,一般利用________和________的方法,将不规则图形转化成________
9.求涂色部分的面积.(结果用小数表示)
面积是________平方米
10.下图是一个平行四边形,它包含了3个三角形,其中两个空白三角形的面积分别是15
和25
.中间涂色的三角形的面积是________
11.长方形长为10厘米,宽为6厘米,AE=CF=1.5厘米,阴影部分的面积是________平方厘米。
四、解答题
12.求下面图中阴影部分的面积.正方形边6cm.
13.如图,一块长方形草地,长方形的长是22米,宽是13米,中间铺了一条石子路。那么草地部分面积有多大?
五、综合题
14.盐渎公园里有块梯形的地,在中间修一条底为5米的平行四边形的路,将这块地分成两部分,计划分别种牡丹和玫瑰.
牡 丹
每棵占地2m2
每棵10元
玫 瑰
每平方米种2棵
每棵6元
(1)这块梯形地的面积是多少平方米?
(2)牡丹能种多少棵?
(3)种玫瑰一共需要多少钱?
六、应用题
15.已知梯形的面积是75平方厘米,求图中阴影部分的面积.
参考答案
一、单选题
1.【答案】
B
【解析】【解答】解:(14+26)×15÷2-3×15=255(平方米)
故答案为:B。
【分析】先计算梯形的面积,再计算平行四边形的面积,用梯形面积减去平行四边形的面积即可。
2.【答案】B
【解析】【解答】因为梯形的面积=(上底+下底)×高÷2,“上底增加3厘米,下底减少3厘米,面积不变”则(上底+下底)的和不变,且面积不变,所以梯形的高不变。
故选:B
【分析】梯形的面积=(上底+下底)×高÷2,若“上底增加3米,下底减少3米,面积不变”则(上底+下底)的和不变,且面积不变,从而得知梯形的高也不变。
3.【答案】C
【解析】【解答】解:设外圆半径是R厘米,内圆半径是r厘米,
R×R÷2-r×r÷2=3
R -r =6
圆环面积:S=π×(R -r )=3.14×6=18.84(平方厘米)
故答案为:C
【分析】外圆半径就是大三角形的直角边长,内圆半径就是小三角形的直角边长;根据阴影部分的面积是3平方厘米计算出外圆半径的平方与内圆半径的平方的差,然后根据圆环面积公式计算面积即可.
二、判断题
4.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。
故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
5.【答案】错误
【解析】【解答】A图与B图的周长相等,面积不相等,原题说法错误.
故答案为:错误.
【分析】根据题意,A图的周长包括一条长和一条宽的长度之和及中间曲线的长度,B图的周长也包括一条长和一条宽的长度之和及中间曲线的长度,长方形的对边相等,所以周长相等,图形B的面积大于图形A的面积,据此解答.
6.【答案】正确
【解析】【解答】根据分析,作图如下:
(1)2×2÷2×2
=4÷2×2
=4(cm2)
(2)2×1+2×2÷2
=2+4÷2
=2+2
=4(cm2)
两图中阴影部分的面积相等,原题说法正确.
故答案为:正确.【分析】(1)第一个图的阴影部分可以分成两个底为2厘米,高为2厘米的相等三角形,据此利用三角形的面积公式计算即可;(2)第二个图的阴影部分可以分成一个长为2厘米,宽为1厘米的长方形与一个底是2厘米,高是2厘米的三角形,将两个图形的面积相加即可得到阴影部分的面积,然后比较两个图的阴影部分的面积大小即可.
三、填空题
7.【答案】533.8
【解析】【解答】7+24+13=44(厘米)
3.14×(44÷2) ÷2-3.14×(24÷2) ÷2
=3.14×484÷2-3.14×144÷2
=759.88-226.08
=533.8(平方厘米)
故答案为:533.8
【分析】阴影部分的面积是大半圆的面积减去空白部分小半圆的面积,先计算大半圆的直径,然后根据圆面积公式计算.
8.【答案】平移;旋转;规则图形
【解析】【解答】解:求不规则图形的面积,一般利用平移和旋转的方法,将不规则图形转化成规则图形.
故答案为:平移;旋转;规则图形【分析】由于不规则图形无法直接计算面积,所以要把不规则图形转化成规则图形来计算面积,这种方法叫作转化法.
9.【答案】
77.04
【解析】【解答】解:12÷2=6(米),
3.14×6 -12×6÷2
=113.04-36
=77.04(平方米)
故答案为:77.04
【分析】用圆面积减去空白部分三角形的面积就是涂色部分的面积。空白部分三角形的高就是圆的半径,由此计算即可。
10.【答案】40
【解析】
11.【答案】10.875
【解析】【解答】解:10×6÷2-(10-1.5)×(6-1.5)÷2
=30-8.5×4.5÷2
=30-38.25÷2
=30-19.125
=10.875
答:阴影面积是10.875
大三角形的面积减去小三角形的面积.
【分析】阴影部分的面积是两个三角形面积的差
四、解答题
12.【答案】解:(6×
)×2
=
=(36﹣28.26)×2
=7.74×2
=15.48(平方厘米),
答:阴影部分的面积是15.48平方厘米
【解析】【分析】首先用正方形的面积减去半径为6厘米的圆面积的
求出阴影部分面积的一半,然后再乘2即可.根据正方形的面积公式:s=a2
,
圆的面积公式:s=πr2
,
把数据代入公式解答.此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式.
13.【答案】
解:22×13-2×22=242(平方米)
答:草地部分面积242平方米。
【解析】【分析】草地部分面积=大长方形的面积-石子路的面积,其中长方形的面积=长×宽,从图中看出,石子路是一个平行四边形,它的高是长方形的长,所以石子路的面积=底×高,据此代入数据作答即可。
五、综合题
14.【答案】(1)解:牡丹园面积:
30×20÷2
=600÷2
=300(平方米)
玫瑰园的面积:
60×20÷2
=1200÷2
=600(平方米)
路的面积;
5×20=100(平方米)
总面积:
300+600+100=1000(平方米)
答:这块梯形地的面积是1000平方米
(2)解:300÷2=150(棵)
答:牡丹能种150棵.
(3)解:600×2×6
=1200×6
=7200(元)
答:种玫瑰一共需要7200元
【解析】【分析】(1)根据三角形的面积公式分别求出牡丹园、玫瑰园的面积,再加上路的面积;再求三者之和即可.(2)用牡丹园的面积除以每棵占地面积,即为能种多少棵牡丹.(3)用玫瑰园的面积乘以2,即为种玫瑰的棵数,再乘以玫瑰的单价,即为种玫瑰一共需要多少钱.
六、应用题
15.【答案】解:8.5×[75×2÷(8.5+6.5)]÷2,
=8.5×10÷2,
=42.5(平方厘米);
答:阴影部分的面积是42.5平方厘米
【解析】【分析】我们用梯形的面积乘以2除以上下底的和就是梯形的高,然后运用三角形的面积公式求出阴影部分的面积.本题运用梯形的面积公式及三角形的面积公式进行解答即可.
