二 笛卡儿坐标系 课件(27张PPT)
文档属性
| 名称 | 二 笛卡儿坐标系 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第4讲 平面解析几何的产生
——数与形的结合
导入新课
坐标思想古已有之(如地理中所用的“经线”和“纬线”),而且有先驱者曾经研究过这个问题,但解析几何真正的发明要归功于法国数学家笛卡儿.
笛卡儿坐标系
勒奈·笛卡儿(Rence Descartes,1596~1650)法国哲学家、物理学家、生理学家和数学家 .解析几何的创始人.
内容解析
笛卡儿简介
世人对笛卡儿的评价
解析几何的创立
笛卡儿的贡献
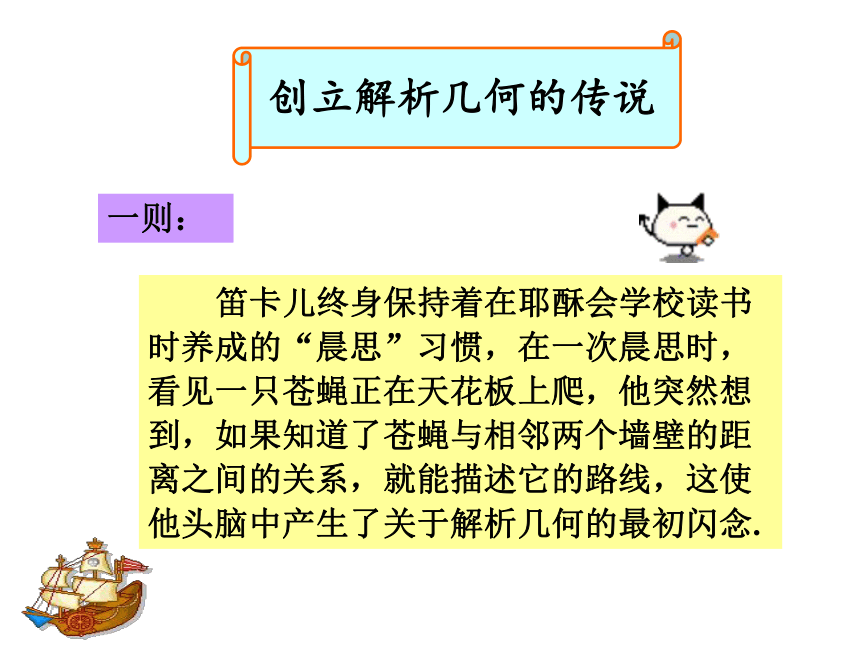
创立解析几何的传说
笛卡儿解析几何的思想
笛卡尔1596年3月31日生于法国的一个贵族家庭.因家境富裕从小多病,学校允许他在床上早读,养成终生“晨思”的习惯.1606年他在欧洲的耶稣会的拉弗莱什学校上学,1616年在普依托大学学习法律与医学,1617年和1619年两次从军,离开军营后,旅行于欧洲,他的学术研究是在军旅和旅行中作出的.1650年2月11日卒于斯德哥尔摩.
笛卡儿简介
一则:
笛卡儿终身保持着在耶酥会学校读书时养成的“晨思”习惯,在一次晨思时,看见一只苍蝇正在天花板上爬,他突然想到,如果知道了苍蝇与相邻两个墙壁的距离之间的关系,就能描述它的路线,这使他头脑中产生了关于解析几何的最初闪念.
创立解析几何的传说
二则:
1619年冬天,笛卡儿随军队驻扎在多瑙河畔的一个村庄,在圣马丁节的前夕(11月10日),他作了三个连贯的梦,从而揭示了解析几何的发现.
1619年,在多瑙河的军营中,笛卡儿开始用大部分的时间来思考他在数学中的新想法:是否可以用代数中的计算过程来代替几何中的证明呢?要这样就必须找到一座能连接几何与代数的桥梁——使几何图形数值化,从而能用数值的方法去解决,即“数形结合”的思想.
解析几何的创立
同年,笛卡儿发现了“一种全新的科学,它可能用一种一般的方法解决所有与量有关的领域中的问题,不论这种量是连续的还是数值的”,这就是他发明的解析几何的方法.
笛卡儿在《方法论》一书中写道:第一,如果要发现真正的知识,必须靠自己去实行整个研究计划,正如一件上好的艺术品或一幢完美的建筑,总是出自一个能人之手;第二,在方法上,必须从怀疑当时哲学的所有内容为出发点,并寻找自明的、确定的原理,在此基础上重新构造出一切科学.
笛卡尔的贡献是多方面的,他是欧洲近代哲学的主要开拓者之一,黑格尔称他为“现代哲学之父”,而他建立解析几何的成就在科学史上有划时代的意义.恩格斯高度评价说:“数学中的转折点是笛卡尔的变数,有了变数,运动进入了数学,有了变数,微分与积分也就立即变成必须.”
笛卡儿的贡献
世人对笛卡儿的评价
数学史家克莱因(M.Kline)这样评价笛卡儿:他只偶尔地史一个数学家,不过像他那样富于智力的人即使只花一部分时间在一个科目上,其工作也必定是有意义的.
法国邮票上的笛卡儿
人们在他的墓碑上刻下了这样一句话:“笛卡尔,欧洲文艺复兴以来,第一个为人类争取并保证理性权利的人.”
笛卡尔堪称17世纪及其后的欧洲哲学界和科学界最有影响的巨匠之一,被誉为“近代科学的始祖”.
1637年笛卡儿出版科著名的著作《方法论》.该书主要是哲学著作,但包括了3个著名的附录:《几何学》、《折光》和《气象》.其中的《几何学》是他唯一的数学著作.书中阐述了解析几何的思想,后人把这本书看作解析几何的开端.
笛卡儿解析几何的思想
笛卡尔《几何》
《几何学》
(共三部分)
第一部分讨论尺规作图,将几何问题化为代数问题,提出“仅用圆与直线的作图问题”.
第二部分讨论曲线的性质.给出解析几何的基本思想,将点与一种斜坐标系下的数对(x,y)联系起来.
第三部分讨论当时流行的代数问题.表讨论代数方程论中“代数方程根的个数”和“笛卡儿符号法则”.
书中第一次出现了变量与函数的概念,笛卡儿所谓的变量是指长度可变而方向不变的线段,还指连续经过坐标轴上所有点的数字变量.正是由于对变量形式的这两种考虑,才使得笛卡儿能够创建一种几何与代数相互渗透的科学,或者说一种把算术、代数和几何统一起来的通用的数学.
解析几何的基本思想:
笛卡儿指出每一对有序实数,即坐标(x,y)都对应于平面上唯一的一个点;反之,平面上每一个点都有唯一的一个坐标(x,y)与之对应.根据这种坐标思想,笛卡儿进一步考虑二元方程f(x,y)=0的性质.x,y的不同数值所确定的平面上许多不同的点形成一条曲线.
这样一个代数方程就可以通过几何直观的方法去处理.反之,可以离开几何图形,用代数的方法研究几何的性质.具有某种性质的点之间有某种关系,“这个关系可以用一个方程来表示”.
笛卡儿把以往对立着的两个研究对象“数”与“形”统一起来,并在数学中引入了变量的思想,从而开拓了变量数学领域,是数学史上一项划时代的变革.
笛卡儿以一个古希腊的数学问题——帕波斯问题举例,求出了双曲线的轨迹方程:
设在平面上给定4条直线,
面上的点C作4条直线分别与
点P, R,Q,S,交角分别等于已知角
求使CP·CR=kCQ·CS(k为常数)
,过平
交于
的点C的轨迹.
E
A
P
G
R
D
S
C
Q
x
y
如图所示
记AP为x,PC为y,经简单的几何分析,他用已知量表示出CR,CQ和CS的值,代入CP·CR=CQ·CS(取k=1),就得到一个关于x和y的二次方程:
证明:
①
其中A,B,C,D是由已知量构成的简单代数式.于是笛卡儿指出,任给x一个值,就得到一个关于y的二次方程,如果我们取无穷多个x值,就得到无穷多个y值,从而得到无穷多个点C,所以点C的轨迹就是方程①所代表的曲线.
笛卡儿选定一条直线AG作为基线,以点A为原点,从A为原点,从A点量起,x值是基线的长度;y值是另外一条直线的长度,该线段从基线出发,与基线成定角.这样,笛卡儿建立了历史上第一个倾斜坐标系.
在《几何学》的第二卷中,笛卡儿考虑了曲线的分类及其性质,用代数方程的直接可解性区分“几何曲线”与“非几何曲线”.他把复杂的高次曲线也看作几何曲线(代数曲线),把不能用代数方程表示的曲线称为“机械曲线”(超越曲线).这样,笛卡儿开辟了全新的曲线领域.
在坐标系和曲线方程的基础上,笛卡儿又提出了一系列新颖的想法.
曲线的次数与坐标轴的选择无关;坐标轴的选取应使曲线方程尽量简单;可以利用表示曲线的方程来求两条不同曲线的交点等.
笛卡儿对韦达所采用的代数符号作了改进:用字母表中末尾几个字母x,y,z……表示未知数;用开头几个字母a,b, c ……表示已知数.他还给出了幂指数的简单表示方法,平方根符号也是笛卡儿首先使用的.在现代的数学文献中,有许多概念以笛卡儿的名字命名如笛卡儿坐标系、笛卡儿乘积、笛卡儿抛物线,等等.
在《几何学》中,笛卡儿充分发挥了代数学的强大威力,利用坐标系把代数和几何结合起来,使解析几何成为一种普遍的方法.从此,数学一改以前的局面,大大地向前迈进了一步.
阿尔巴尼亚邮票上的笛卡儿
课堂小结
笛卡儿的解析几何的基本思想:
(1)用有序数对表示点的坐标;
(2)把互相关联的两个未知数的代数方程,看成平面上的一条曲线.
第4讲 平面解析几何的产生
——数与形的结合
导入新课
坐标思想古已有之(如地理中所用的“经线”和“纬线”),而且有先驱者曾经研究过这个问题,但解析几何真正的发明要归功于法国数学家笛卡儿.
笛卡儿坐标系
勒奈·笛卡儿(Rence Descartes,1596~1650)法国哲学家、物理学家、生理学家和数学家 .解析几何的创始人.
内容解析
笛卡儿简介
世人对笛卡儿的评价
解析几何的创立
笛卡儿的贡献
创立解析几何的传说
笛卡儿解析几何的思想
笛卡尔1596年3月31日生于法国的一个贵族家庭.因家境富裕从小多病,学校允许他在床上早读,养成终生“晨思”的习惯.1606年他在欧洲的耶稣会的拉弗莱什学校上学,1616年在普依托大学学习法律与医学,1617年和1619年两次从军,离开军营后,旅行于欧洲,他的学术研究是在军旅和旅行中作出的.1650年2月11日卒于斯德哥尔摩.
笛卡儿简介
一则:
笛卡儿终身保持着在耶酥会学校读书时养成的“晨思”习惯,在一次晨思时,看见一只苍蝇正在天花板上爬,他突然想到,如果知道了苍蝇与相邻两个墙壁的距离之间的关系,就能描述它的路线,这使他头脑中产生了关于解析几何的最初闪念.
创立解析几何的传说
二则:
1619年冬天,笛卡儿随军队驻扎在多瑙河畔的一个村庄,在圣马丁节的前夕(11月10日),他作了三个连贯的梦,从而揭示了解析几何的发现.
1619年,在多瑙河的军营中,笛卡儿开始用大部分的时间来思考他在数学中的新想法:是否可以用代数中的计算过程来代替几何中的证明呢?要这样就必须找到一座能连接几何与代数的桥梁——使几何图形数值化,从而能用数值的方法去解决,即“数形结合”的思想.
解析几何的创立
同年,笛卡儿发现了“一种全新的科学,它可能用一种一般的方法解决所有与量有关的领域中的问题,不论这种量是连续的还是数值的”,这就是他发明的解析几何的方法.
笛卡儿在《方法论》一书中写道:第一,如果要发现真正的知识,必须靠自己去实行整个研究计划,正如一件上好的艺术品或一幢完美的建筑,总是出自一个能人之手;第二,在方法上,必须从怀疑当时哲学的所有内容为出发点,并寻找自明的、确定的原理,在此基础上重新构造出一切科学.
笛卡尔的贡献是多方面的,他是欧洲近代哲学的主要开拓者之一,黑格尔称他为“现代哲学之父”,而他建立解析几何的成就在科学史上有划时代的意义.恩格斯高度评价说:“数学中的转折点是笛卡尔的变数,有了变数,运动进入了数学,有了变数,微分与积分也就立即变成必须.”
笛卡儿的贡献
世人对笛卡儿的评价
数学史家克莱因(M.Kline)这样评价笛卡儿:他只偶尔地史一个数学家,不过像他那样富于智力的人即使只花一部分时间在一个科目上,其工作也必定是有意义的.
法国邮票上的笛卡儿
人们在他的墓碑上刻下了这样一句话:“笛卡尔,欧洲文艺复兴以来,第一个为人类争取并保证理性权利的人.”
笛卡尔堪称17世纪及其后的欧洲哲学界和科学界最有影响的巨匠之一,被誉为“近代科学的始祖”.
1637年笛卡儿出版科著名的著作《方法论》.该书主要是哲学著作,但包括了3个著名的附录:《几何学》、《折光》和《气象》.其中的《几何学》是他唯一的数学著作.书中阐述了解析几何的思想,后人把这本书看作解析几何的开端.
笛卡儿解析几何的思想
笛卡尔《几何》
《几何学》
(共三部分)
第一部分讨论尺规作图,将几何问题化为代数问题,提出“仅用圆与直线的作图问题”.
第二部分讨论曲线的性质.给出解析几何的基本思想,将点与一种斜坐标系下的数对(x,y)联系起来.
第三部分讨论当时流行的代数问题.表讨论代数方程论中“代数方程根的个数”和“笛卡儿符号法则”.
书中第一次出现了变量与函数的概念,笛卡儿所谓的变量是指长度可变而方向不变的线段,还指连续经过坐标轴上所有点的数字变量.正是由于对变量形式的这两种考虑,才使得笛卡儿能够创建一种几何与代数相互渗透的科学,或者说一种把算术、代数和几何统一起来的通用的数学.
解析几何的基本思想:
笛卡儿指出每一对有序实数,即坐标(x,y)都对应于平面上唯一的一个点;反之,平面上每一个点都有唯一的一个坐标(x,y)与之对应.根据这种坐标思想,笛卡儿进一步考虑二元方程f(x,y)=0的性质.x,y的不同数值所确定的平面上许多不同的点形成一条曲线.
这样一个代数方程就可以通过几何直观的方法去处理.反之,可以离开几何图形,用代数的方法研究几何的性质.具有某种性质的点之间有某种关系,“这个关系可以用一个方程来表示”.
笛卡儿把以往对立着的两个研究对象“数”与“形”统一起来,并在数学中引入了变量的思想,从而开拓了变量数学领域,是数学史上一项划时代的变革.
笛卡儿以一个古希腊的数学问题——帕波斯问题举例,求出了双曲线的轨迹方程:
设在平面上给定4条直线,
面上的点C作4条直线分别与
点P, R,Q,S,交角分别等于已知角
求使CP·CR=kCQ·CS(k为常数)
,过平
交于
的点C的轨迹.
E
A
P
G
R
D
S
C
Q
x
y
如图所示
记AP为x,PC为y,经简单的几何分析,他用已知量表示出CR,CQ和CS的值,代入CP·CR=CQ·CS(取k=1),就得到一个关于x和y的二次方程:
证明:
①
其中A,B,C,D是由已知量构成的简单代数式.于是笛卡儿指出,任给x一个值,就得到一个关于y的二次方程,如果我们取无穷多个x值,就得到无穷多个y值,从而得到无穷多个点C,所以点C的轨迹就是方程①所代表的曲线.
笛卡儿选定一条直线AG作为基线,以点A为原点,从A为原点,从A点量起,x值是基线的长度;y值是另外一条直线的长度,该线段从基线出发,与基线成定角.这样,笛卡儿建立了历史上第一个倾斜坐标系.
在《几何学》的第二卷中,笛卡儿考虑了曲线的分类及其性质,用代数方程的直接可解性区分“几何曲线”与“非几何曲线”.他把复杂的高次曲线也看作几何曲线(代数曲线),把不能用代数方程表示的曲线称为“机械曲线”(超越曲线).这样,笛卡儿开辟了全新的曲线领域.
在坐标系和曲线方程的基础上,笛卡儿又提出了一系列新颖的想法.
曲线的次数与坐标轴的选择无关;坐标轴的选取应使曲线方程尽量简单;可以利用表示曲线的方程来求两条不同曲线的交点等.
笛卡儿对韦达所采用的代数符号作了改进:用字母表中末尾几个字母x,y,z……表示未知数;用开头几个字母a,b, c ……表示已知数.他还给出了幂指数的简单表示方法,平方根符号也是笛卡儿首先使用的.在现代的数学文献中,有许多概念以笛卡儿的名字命名如笛卡儿坐标系、笛卡儿乘积、笛卡儿抛物线,等等.
在《几何学》中,笛卡儿充分发挥了代数学的强大威力,利用坐标系把代数和几何结合起来,使解析几何成为一种普遍的方法.从此,数学一改以前的局面,大大地向前迈进了一步.
阿尔巴尼亚邮票上的笛卡儿
课堂小结
笛卡儿的解析几何的基本思想:
(1)用有序数对表示点的坐标;
(2)把互相关联的两个未知数的代数方程,看成平面上的一条曲线.
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
