2019秋湘教版九年级数学上册第三章:图形的相似 周测(3.2平行线分线段成比例)(含答案)
文档属性
| 名称 | 2019秋湘教版九年级数学上册第三章:图形的相似 周测(3.2平行线分线段成比例)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览

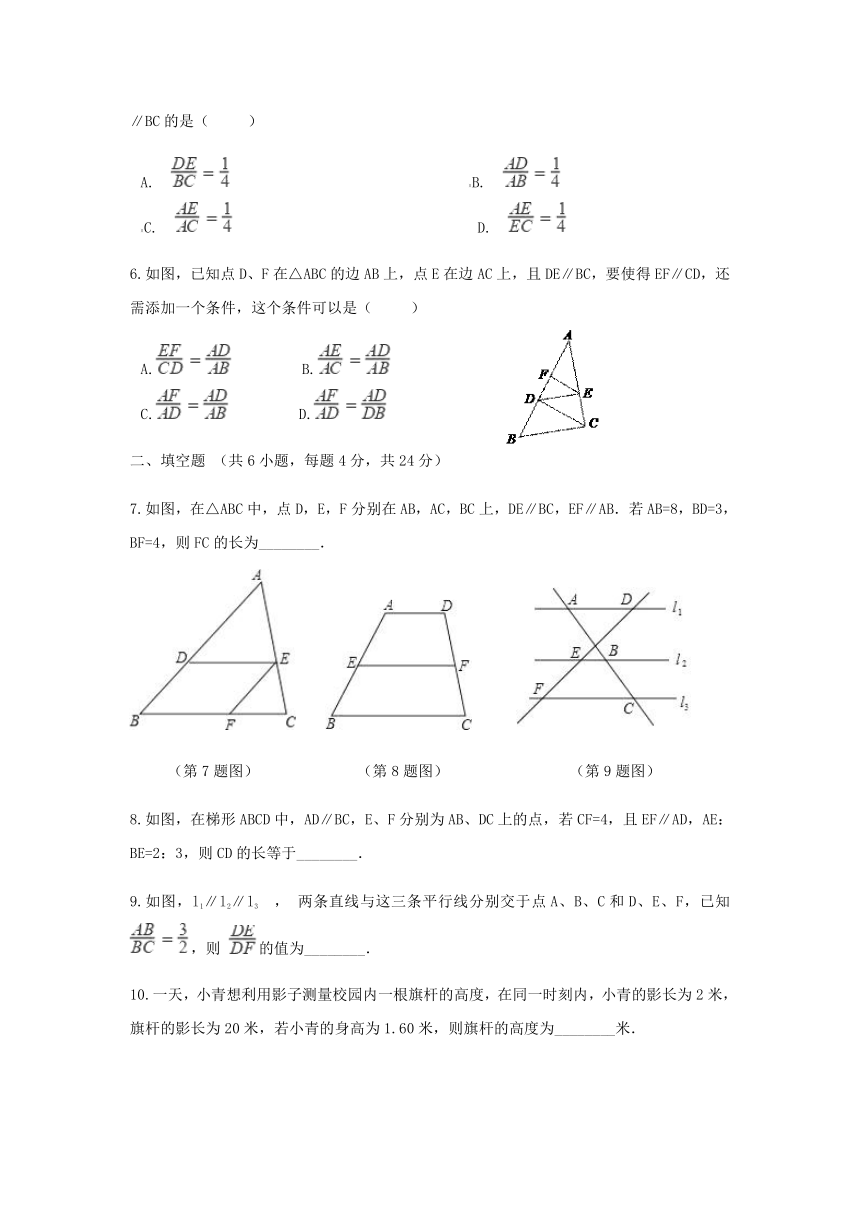

文档简介
2019秋湘教版九年级数学上册第三章图形的相似周测3.2学案设计
一、选择题(共6小题,每题4分,共24分)
1.如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是(?? )
A.?EG=4GC?????????????????B.?EG=3GC???????????
C.?EG= GC????????????????D.?EG=2GC
(第1题图) (第2题图) (第3题图)
2.如图,在△ABC中,点D、E分别是边AB,AC上的点,且DE∥BC,若 ,DE=3,则BC的长度是(?? )
A.?6??????B.?8??????? C.?9??????D.?10
3.如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( ??)
A.?11????B.?12?????C.?13??????D.?14
4.如图,在△ABC中,点D,E分别在边BA,CA的延长线上, ?=2,那么下列条件中能判断DE∥BC的是(?? )
A.???????? ?B.??????????????????????????
?C.?? ???????D.?
5.在△ABC中,点D,E分别在AB,AC上,如果AD:BD=1:3,那么下列条件中能够判断DE∥BC的是(?? )
A.????????????? ??B.????????????C.????? ????????D.?
6.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是(?? )
A. B.
C. D.
二、填空题 (共6小题,每题4分,共24分)
7.如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为________.
(第7题图) (第8题图) (第9题图)
8.如图,在梯形ABCD中,AD∥BC,E、F分别为AB、DC上的点,若CF=4,且EF∥AD,AE:BE=2:3,则CD的长等于________.
9.如图,l1∥l2∥l3 , 两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知 ,则 的值为________.
10.一天,小青想利用影子测量校园内一根旗杆的高度,在同一时刻内,小青的影长为2米,旗杆的影长为20米,若小青的身高为1.60米,则旗杆的高度为________米.
(第10题图) (第11题图) (第12题图)
11.如图,在矩形 中, 是边 的中点,连接 交对角线 于点 ,若 , ,则 的长为________.
12.如图,直线l1∥l2∥l3 , 直线AC交l1 , l2 , l3 , 于点A,B,C;直线DF交l1 , l2 , l3于点D,E,F,已知 ,则 =________。
三、解答题 (共5小题,共52分)
13.已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.
?
14.如图,在△ABC中,DE∥BC,已知CD=1,BC=1.8,DE=1.5,求AD的长.
?
15.如图,a∥b∥c,
(1)若AC=6cm,EC=4cm,BD=8cm,则线段DF的长度是多少厘米?
(2)若AE:EC=5:2,DB=5cm,则线段DF的长度是多少厘米?
?
16.如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长.
?
17.如图,△ABC中,DE∥BC,如果AD = 2,DB = 3,AE = 4,求AC的长.
参考答案
1.B 2.C 3. B 4.D 5.C 6.B
7.1.5 8.20/3 9.3/5 10.16 11.10/3 12.2
13.证明:∵AB//DE, ∴FB:BD=FA:AE. ∵BC//EF, ∴ BD:FB=DC:CE. ∵AC//DF, ∴ EA:AF=EC:CD. ∴ DC:CE=CE:DC. ∴ CE=DC.同理可得:AE=AF,BD=BF. ∴ A,B,C是ΔDEF各边的中点
14.解:∵DE//BC, ∴ΔADF∽ΔACB. ∴EB:BC=AD:AC,即ED:BC=AD :(AD+CD),1.5:1.8= AD :(AD+1),解得AD=5.
15.解:(1)∵a//b//c, ∴AC:EC=BD:DF,即6:4=8:DF,解得DF=16/3;
(2)∵AE:EC=5:2,(AC+EC):EC=5:2.AC:EC=3:2. ∵a//b//c, ∴AC:EC=BD:DF,即3:2=5:DF, ∴DF=10/3.
16.解; ∵EF∥BC, ∴AE:BE=AF:FC,即12:18=14:FC. ∴FC=21. ∵FD∥AB, ∴CF:AF=CD:BD,即21:14=24:BD. ∴BD=16. ∵EF∥BC ,FD∥AB, ∴四边形EFDB是平行四边形. ∴EF=BD=16.
17.解:∵DE//BC, ∴AD:BD=AE:EC,即2:3=4:EC. ∴EC=6. ∴AC=AE+EC=4+6=10.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
