北师大版高中数学必修4教案:1.6.2余弦函数的性质
文档属性
| 名称 | 北师大版高中数学必修4教案:1.6.2余弦函数的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览


文档简介
§6 余弦函数的图像和性质
一、教学目标
1.知识与技能
(1)能根据诱导公式,利用正弦函数的图像,画出余弦函数的图像.
(2)会利用余弦函数的图像进一步理解和研究余弦函数的定义域、值域、奇偶性、周期性、单调性、最大值和最小值等性质.
2.过程与方法
通过利用类比正弦函数性质研究余弦函数性质的学习过程,体会类比的思想方法.
3.情感、态度与价值观
通过类比、知识迁移的学习方法,提高探究新知的能力,并通过正弦函数和余弦函数的图像与性质的类比,了解正弦函数、余弦函数的区别与内在联系.
二、教材分析
教材中通过类比正弦函数,展开了对余弦函数相关内容的学习.这样编写突出了正弦函数与余弦函数的联系,体现了研究问题的一般思路和方法.
余弦函数图像既可以通过诱导公式由正弦函数图像得到,又可以通过描点法得出,教材中淡化了对后者的讲解.
三、重点和难点
本节的重点:余弦函数的图像和性质.
本节的难点:由正弦函数图像得到余弦函数的图像.
四、教学方法与手段
教学方法:启发、引导、发现、概括、归纳
教学手段:多媒体辅助教学.
五、教学过程
(一)创设情境,揭示课题
教师引出课题在上节课中,我们知道正弦函数y=sinx的图像,是通过等分单位圆、平移正弦线而得到的,在精确度要求不高时,可以采用五点作图法得到.那么,对于余弦函数y=cosx的图像,是不是也是这样得到的呢?有没有更好的方法呢?这节课我们来学习余弦函数的图像与性质.
(二)探究新知
1.余弦函数y=cosx的图像
由诱导公式有:y=cosx=cos(-x)=sin[-(-x)]=sin(x+)
结论:(1)y=cosx,x(R与函数y=sin(x+) x(R的图像相同
(2)将y=sinx的图象向左平移个单位,即得y=cosx的图像
(3)也同样可用五点法作图:y=cosx,x([0,2(]的五个点关键是(0,1) (,0) ((,-1) (,0) (2(,1)
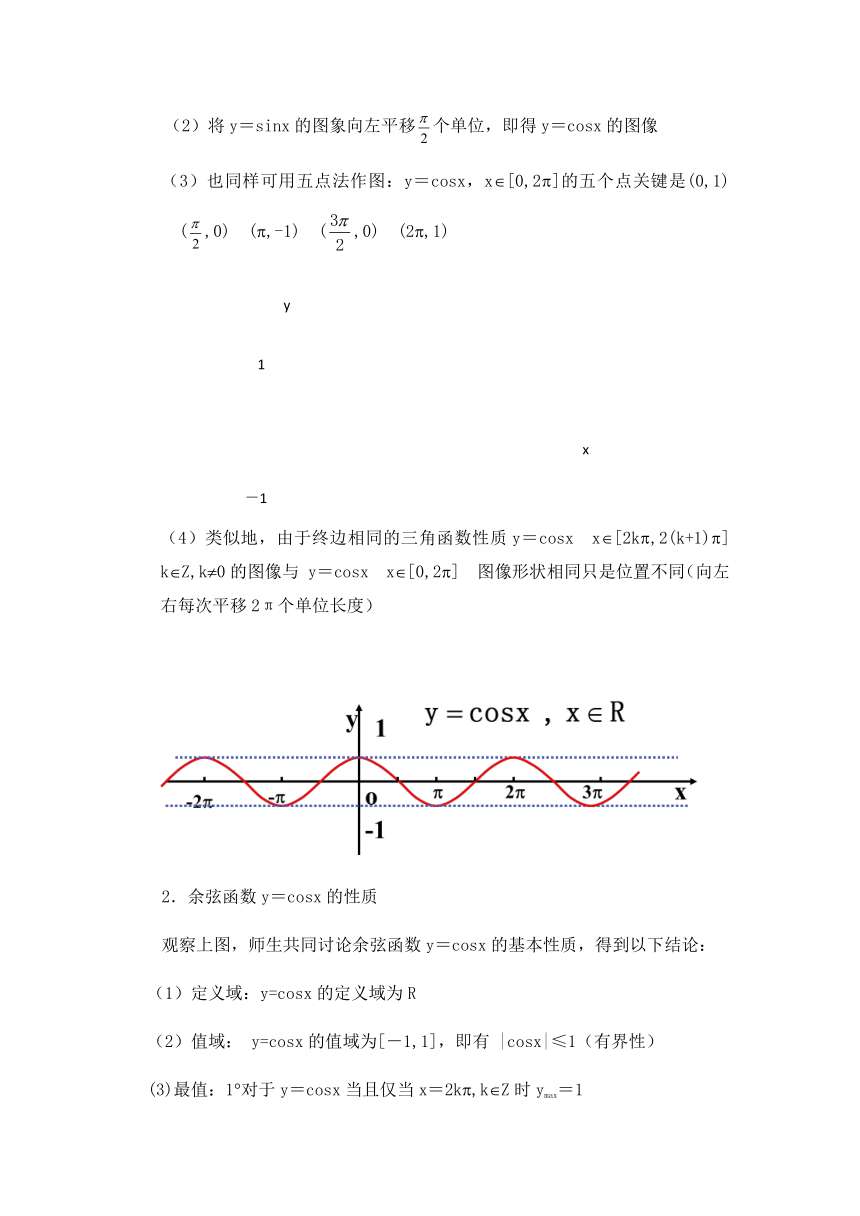
(4)类似地,由于终边相同的三角函数性质y=cosx x([2k(,2(k+1)(] k(Z,k(0的图像与 y=cosx x([0,2(] 图像形状相同只是位置不同(向左右每次平移2π个单位长度)
2.余弦函数y=cosx的性质
观察上图,师生共同讨论余弦函数y=cosx的基本性质,得到以下结论:
(1)定义域:y=cosx的定义域为R
(2)值域: y=cosx的值域为[-1,1],即有 |cosx|≤1(有界性)
(3)最值:1(对于y=cosx当且仅当x=2k(,k(Z时ymax=1
当且仅当时x=2k(+π, k(Z时ymin=-1
2(当2k(-0
当2k(+教师可引导、点拨学生先截取一段来看,选哪一段呢?通过学生充分讨论后确定,学生若选取区间,教师应追问,为什么选区间,而不是选区间,引导学生思考.
(4)周期性:y=cosx的最小正周期为2(
(5)奇偶性
cos(-x)=cosx (x∈R) y=cosx (x∈R)是偶函数
(6)单调性
增区间为[(2k-1)π, 2kπ](k∈Z),其值从-1增至1;
减区间为[2kπ,(2k+1)π](k∈Z),其值从1减至-1.
(三)巩固深化,发展思维引导学生分析对比正弦函数、余弦函数的图像,思考这两个函数图像的异同点,思考函数图像的平移对函数性质的影响.
例1.请画出函数y=cosx -1的简图,并根据图像讨论函数的性质。
解:按五个关键点列表,根据表中数据画出简图
观察图像得出y=cosx-1的性质
函数
y=cosx-1
定义域
R
值域
奇偶性
偶函数
周期性
单调性
最大值与最小值
对称性
对称中心坐标为;
对称轴方程为
2.课堂练习
教材33页的练习1、2、3、4、5
(四)思考交流
根据余弦函数的图像,求满足的的集合.
分析:先在一个周期内解,得.
再考虑周期性,可得满足的的集合为
(五)归纳整理,整体认识
(1)请学生回顾本节课所学过的知识内容有哪些?所涉及的主要数学思想方法有那些?
(2)在本节课的学习过程中,还有那些不明白的地方,请向老师提出.
(3)你在这节课中的表现怎样?你的体会是什么?
(六)课后作业
作业:课本34页A组第2,3,4,5题
六、教学反思:
本节课,由正弦函数的图像通过平移得出余弦函数的图像,再根据余弦函数的图像得出其性质,使同学们对余弦函数的概念有更深的体会;会用联系的观点看问题,建立数形结合的思想,激发学习的学习积极性;培养学生分析问题、解决问题的能力;让学生体验自身探索成功的喜悦感,培养学生的自信心;使学生认识到转化“矛盾”是解决问题的有效途经;培养学生形成实事求是的科学态度和锲而不舍的钻研精神.
(设计者:西安市第一中学 )
一、教学目标
1.知识与技能
(1)能根据诱导公式,利用正弦函数的图像,画出余弦函数的图像.
(2)会利用余弦函数的图像进一步理解和研究余弦函数的定义域、值域、奇偶性、周期性、单调性、最大值和最小值等性质.
2.过程与方法
通过利用类比正弦函数性质研究余弦函数性质的学习过程,体会类比的思想方法.
3.情感、态度与价值观
通过类比、知识迁移的学习方法,提高探究新知的能力,并通过正弦函数和余弦函数的图像与性质的类比,了解正弦函数、余弦函数的区别与内在联系.
二、教材分析
教材中通过类比正弦函数,展开了对余弦函数相关内容的学习.这样编写突出了正弦函数与余弦函数的联系,体现了研究问题的一般思路和方法.
余弦函数图像既可以通过诱导公式由正弦函数图像得到,又可以通过描点法得出,教材中淡化了对后者的讲解.
三、重点和难点
本节的重点:余弦函数的图像和性质.
本节的难点:由正弦函数图像得到余弦函数的图像.
四、教学方法与手段
教学方法:启发、引导、发现、概括、归纳
教学手段:多媒体辅助教学.
五、教学过程
(一)创设情境,揭示课题
教师引出课题在上节课中,我们知道正弦函数y=sinx的图像,是通过等分单位圆、平移正弦线而得到的,在精确度要求不高时,可以采用五点作图法得到.那么,对于余弦函数y=cosx的图像,是不是也是这样得到的呢?有没有更好的方法呢?这节课我们来学习余弦函数的图像与性质.
(二)探究新知
1.余弦函数y=cosx的图像
由诱导公式有:y=cosx=cos(-x)=sin[-(-x)]=sin(x+)
结论:(1)y=cosx,x(R与函数y=sin(x+) x(R的图像相同
(2)将y=sinx的图象向左平移个单位,即得y=cosx的图像
(3)也同样可用五点法作图:y=cosx,x([0,2(]的五个点关键是(0,1) (,0) ((,-1) (,0) (2(,1)
(4)类似地,由于终边相同的三角函数性质y=cosx x([2k(,2(k+1)(] k(Z,k(0的图像与 y=cosx x([0,2(] 图像形状相同只是位置不同(向左右每次平移2π个单位长度)
2.余弦函数y=cosx的性质
观察上图,师生共同讨论余弦函数y=cosx的基本性质,得到以下结论:
(1)定义域:y=cosx的定义域为R
(2)值域: y=cosx的值域为[-1,1],即有 |cosx|≤1(有界性)
(3)最值:1(对于y=cosx当且仅当x=2k(,k(Z时ymax=1
当且仅当时x=2k(+π, k(Z时ymin=-1
2(当2k(-
当2k(+
(4)周期性:y=cosx的最小正周期为2(
(5)奇偶性
cos(-x)=cosx (x∈R) y=cosx (x∈R)是偶函数
(6)单调性
增区间为[(2k-1)π, 2kπ](k∈Z),其值从-1增至1;
减区间为[2kπ,(2k+1)π](k∈Z),其值从1减至-1.
(三)巩固深化,发展思维引导学生分析对比正弦函数、余弦函数的图像,思考这两个函数图像的异同点,思考函数图像的平移对函数性质的影响.
例1.请画出函数y=cosx -1的简图,并根据图像讨论函数的性质。
解:按五个关键点列表,根据表中数据画出简图
观察图像得出y=cosx-1的性质
函数
y=cosx-1
定义域
R
值域
奇偶性
偶函数
周期性
单调性
最大值与最小值
对称性
对称中心坐标为;
对称轴方程为
2.课堂练习
教材33页的练习1、2、3、4、5
(四)思考交流
根据余弦函数的图像,求满足的的集合.
分析:先在一个周期内解,得.
再考虑周期性,可得满足的的集合为
(五)归纳整理,整体认识
(1)请学生回顾本节课所学过的知识内容有哪些?所涉及的主要数学思想方法有那些?
(2)在本节课的学习过程中,还有那些不明白的地方,请向老师提出.
(3)你在这节课中的表现怎样?你的体会是什么?
(六)课后作业
作业:课本34页A组第2,3,4,5题
六、教学反思:
本节课,由正弦函数的图像通过平移得出余弦函数的图像,再根据余弦函数的图像得出其性质,使同学们对余弦函数的概念有更深的体会;会用联系的观点看问题,建立数形结合的思想,激发学习的学习积极性;培养学生分析问题、解决问题的能力;让学生体验自身探索成功的喜悦感,培养学生的自信心;使学生认识到转化“矛盾”是解决问题的有效途经;培养学生形成实事求是的科学态度和锲而不舍的钻研精神.
(设计者:西安市第一中学 )
