北师大版高中数学必修4教案:1.8函数y=Asin(ωxφ)的图像和性质(第1课时)
文档属性
| 名称 | 北师大版高中数学必修4教案:1.8函数y=Asin(ωxφ)的图像和性质(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 61.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 14:56:45 | ||
图片预览


文档简介
§8.1 函数的图像(第一课时)
一、教学目标
知识与技能:
(1)理解三个参数A、ω、φ对函数y=Asin x, y=sin(x+φ)和y=sinωx图像的影响;
(2)揭示函数y=Asin x, y=sin(x+φ)和y=sinωx的图像与正弦曲线的变换关系。
2.过程与方法:
(1)增强学生的作图能力;
(2)通过探究变换过程,使学生掌握从特殊到一般,从具体到抽象的化归思想方法,从而达到从感性认识到理性认识的飞跃
(3)在难点突破环节,培养学生全面分析、抽象、概括的能力。
3.情感态度、价值观:
通过对曲线的伸缩、平移等变换,体会三角形函数曲线的平滑,流畅美,在自主探究的过程中,培养学生勇于探索的精神和善于合作的意识。
二、教材分析
本节课是在前面学习了正弦函数和余弦函数的图像和性质的基础上对正弦函数图像的深化和拓展,由此进一步理解与的图像间的变换关系,教材通过例1,例2,例3分别讨论了函数y=Asinx,y=sin(x+φ),y=sinωx与函数y=sinx的关系,归纳分析出参数对图像的影响。这样设计是为了给学生提供观察问题的视角,希望学生能感受参数对函数图像的影响,在此基础上,再利用函数的图像,进一步讨论所给函数的其他性质,经过这样的过程,最后抽象概括出从函数y=sinx的图像到函数y=Asinx的图像,或从函数y=sinx的图像到函数y=sin(x+φ)的图像,或从函数y=sinx的图像到函数y=sinωx的图像所需的图像变换的步骤。可以看出,教材采用了有简单到复杂的设计,较完整地体现了图形的压缩变换、平移变换过程,是对一般图像变换内容的补充和复习,是函数图象伸缩、平移变换的特例。
同时本节的课标要求是结合具体实例,能利用五点法画出函数y=Asin x, y=sin(x+φ)和y=sinωx的图像,并观察参数A,φ,ω对函数图像变化的影响,同时结合具体函数图像的变化,使学生领会由简单到复杂,特殊到一般的化归思想,本节知识是学习函数图像变换综合应用的基础,在教材地位上显得十分重要,因此这节课的内容是本章的重点、难点之一。
三、教学重点和难点
重点是:考察参数对函数图像变化的影响,理解函数图像到y=Asin x, y=sin(x+φ)和y=sinωx的图像变化过程,借助图像说明函数性质的变化。
难点是:归纳概括函数图像到y=Asin x, y=sin(x+φ)和y=sinωx的图像变化过程。
四、教学方法与手段
让学生动脑想,动手做,自主探究图像与图像之间的变换关系,达到深化理解的目的。
五、教学过程
(一)探究对函数的影响
问题1:利用五点法在同一坐标系中作出函数与的简图.并指出它们的图像与的关系.
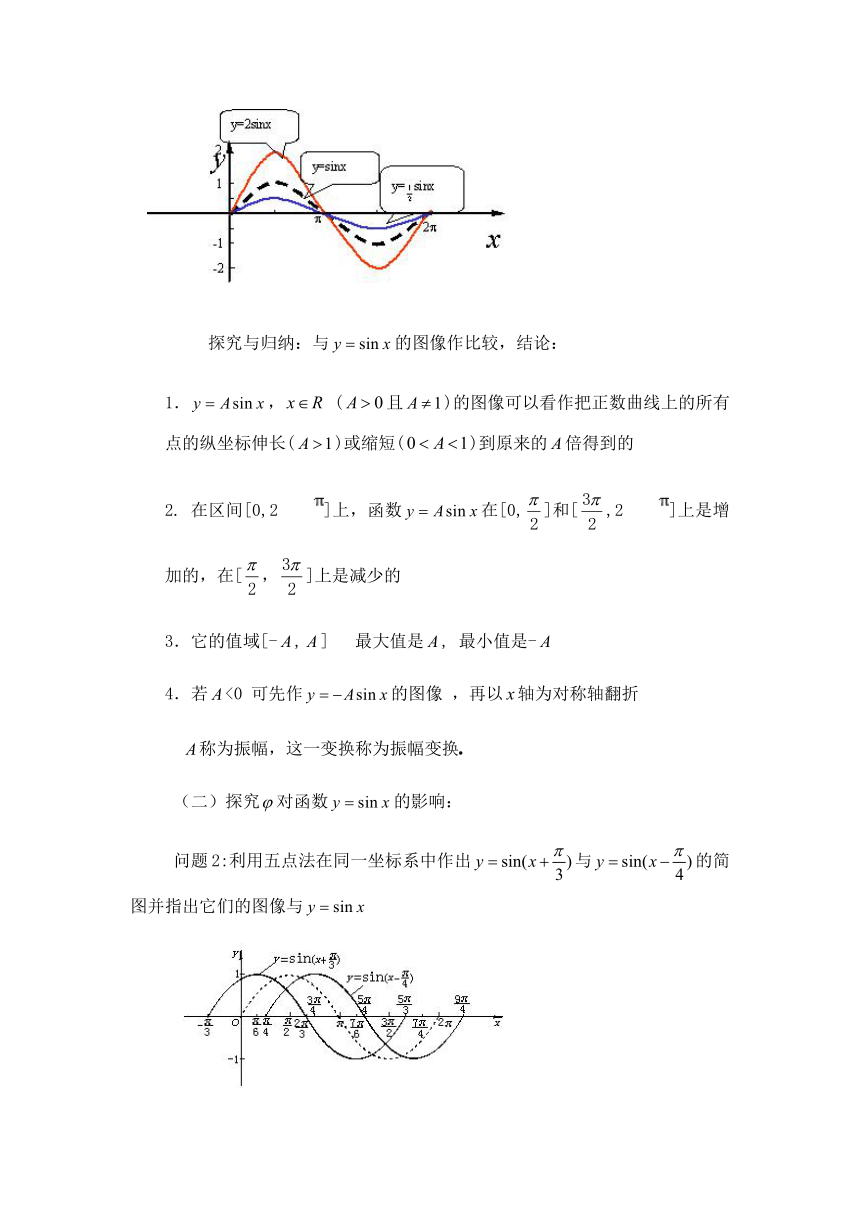
探究与归纳:与的图像作比较,结论:
1., (且)的图像可以看作把正数曲线上的所有点的纵坐标伸长()或缩短()到原来的倍得到的
2. 在区间[0,2]上,函数在[0,]和[,2]上是增加的,在[,]上是减少的
3.它的值域[-,] 最大值是, 最小值是-
4.若<0 可先作的图像 ,再以轴为对称轴翻折
称为振幅,这一变换称为振幅变换
(二)探究对函数的影响:
问题2:利用五点法在同一坐标系中作出与的简图并指出它们的图像与
探究与归纳:
1.一般地,函数, (其中≠0)的图像,可以看作把正弦曲线上所有点向左(当>0时)或向右(当<0时=平行移动||个单位长度而得到 (用平移法注意讲清方向:“左加”“右减”)
与的图像只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换
2.它的值域[-1,1],最大值是1, 最小值是-1
3. 称为初相,x+φ为相位
(三)、探究对函数的影响:
问题3:利用五点法在同一坐标系中作出与的简图.并指出它们的图像与的关系.
探究与归纳:与的图像作比较 :
1.函数, (且)的图像,可看作把正弦曲线上所有点的横坐标缩短()或伸长()到原来的倍(纵坐标不变)
2.它的值域[-1,1],最大值是1, 最小值是-1
3.若则可用诱导公式将符号“提出”再作图,决定了函数的周期T=,这一变换称为周期变换,周期的倒数f= =为频率
设计意图:
五点法作图如何取到关键的五点的坐标,并结合正弦曲线的特点指出如何作图.
问题1、2、3,通过演示图像的伸缩、左、右、上、下平移,引导学生观察、分析,从特殊到一般,从具体到抽象,去总结出、、与的图像之间的联系.
引导学生对所学的知识、数学思想方法进行归纳小结.
(四)巩固练习:课本P46 练习1-2
(五)小结:(由学生小结,教师补充、规范)
本节课主要学习了通过“五点作图法”正确找出函数y=sin x到y=Asin x, y=sin(x+φ)和y=sinωx的图像变换规律,能够自主说明各函数的性质变化,体现了数形结合、化归的数学思想方法。
(六)作业:课本P46 练习1 3 课本P52 练习2 1
六、教学反思
本节课用简谐振动中的位移与时间的图像引入新课,创设情境,激发学生学习的兴趣;通过问题链的设置,让学生先动手用五点法作图,树立起数形结合的思想,然后利用电脑动态演示图像的变换过程,突破传统教学上的难点。通过实践练习,整个教学过程中,让学生动手探究,教师追问,每个知识都由学生通过活动、探究、体验来获得,使学生真正成为学习课程的主体。
(设计者:西安市第一中学 )
一、教学目标
知识与技能:
(1)理解三个参数A、ω、φ对函数y=Asin x, y=sin(x+φ)和y=sinωx图像的影响;
(2)揭示函数y=Asin x, y=sin(x+φ)和y=sinωx的图像与正弦曲线的变换关系。
2.过程与方法:
(1)增强学生的作图能力;
(2)通过探究变换过程,使学生掌握从特殊到一般,从具体到抽象的化归思想方法,从而达到从感性认识到理性认识的飞跃
(3)在难点突破环节,培养学生全面分析、抽象、概括的能力。
3.情感态度、价值观:
通过对曲线的伸缩、平移等变换,体会三角形函数曲线的平滑,流畅美,在自主探究的过程中,培养学生勇于探索的精神和善于合作的意识。
二、教材分析
本节课是在前面学习了正弦函数和余弦函数的图像和性质的基础上对正弦函数图像的深化和拓展,由此进一步理解与的图像间的变换关系,教材通过例1,例2,例3分别讨论了函数y=Asinx,y=sin(x+φ),y=sinωx与函数y=sinx的关系,归纳分析出参数对图像的影响。这样设计是为了给学生提供观察问题的视角,希望学生能感受参数对函数图像的影响,在此基础上,再利用函数的图像,进一步讨论所给函数的其他性质,经过这样的过程,最后抽象概括出从函数y=sinx的图像到函数y=Asinx的图像,或从函数y=sinx的图像到函数y=sin(x+φ)的图像,或从函数y=sinx的图像到函数y=sinωx的图像所需的图像变换的步骤。可以看出,教材采用了有简单到复杂的设计,较完整地体现了图形的压缩变换、平移变换过程,是对一般图像变换内容的补充和复习,是函数图象伸缩、平移变换的特例。
同时本节的课标要求是结合具体实例,能利用五点法画出函数y=Asin x, y=sin(x+φ)和y=sinωx的图像,并观察参数A,φ,ω对函数图像变化的影响,同时结合具体函数图像的变化,使学生领会由简单到复杂,特殊到一般的化归思想,本节知识是学习函数图像变换综合应用的基础,在教材地位上显得十分重要,因此这节课的内容是本章的重点、难点之一。
三、教学重点和难点
重点是:考察参数对函数图像变化的影响,理解函数图像到y=Asin x, y=sin(x+φ)和y=sinωx的图像变化过程,借助图像说明函数性质的变化。
难点是:归纳概括函数图像到y=Asin x, y=sin(x+φ)和y=sinωx的图像变化过程。
四、教学方法与手段
让学生动脑想,动手做,自主探究图像与图像之间的变换关系,达到深化理解的目的。
五、教学过程
(一)探究对函数的影响
问题1:利用五点法在同一坐标系中作出函数与的简图.并指出它们的图像与的关系.
探究与归纳:与的图像作比较,结论:
1., (且)的图像可以看作把正数曲线上的所有点的纵坐标伸长()或缩短()到原来的倍得到的
2. 在区间[0,2]上,函数在[0,]和[,2]上是增加的,在[,]上是减少的
3.它的值域[-,] 最大值是, 最小值是-
4.若<0 可先作的图像 ,再以轴为对称轴翻折
称为振幅,这一变换称为振幅变换
(二)探究对函数的影响:
问题2:利用五点法在同一坐标系中作出与的简图并指出它们的图像与
探究与归纳:
1.一般地,函数, (其中≠0)的图像,可以看作把正弦曲线上所有点向左(当>0时)或向右(当<0时=平行移动||个单位长度而得到 (用平移法注意讲清方向:“左加”“右减”)
与的图像只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换
2.它的值域[-1,1],最大值是1, 最小值是-1
3. 称为初相,x+φ为相位
(三)、探究对函数的影响:
问题3:利用五点法在同一坐标系中作出与的简图.并指出它们的图像与的关系.
探究与归纳:与的图像作比较 :
1.函数, (且)的图像,可看作把正弦曲线上所有点的横坐标缩短()或伸长()到原来的倍(纵坐标不变)
2.它的值域[-1,1],最大值是1, 最小值是-1
3.若则可用诱导公式将符号“提出”再作图,决定了函数的周期T=,这一变换称为周期变换,周期的倒数f= =为频率
设计意图:
五点法作图如何取到关键的五点的坐标,并结合正弦曲线的特点指出如何作图.
问题1、2、3,通过演示图像的伸缩、左、右、上、下平移,引导学生观察、分析,从特殊到一般,从具体到抽象,去总结出、、与的图像之间的联系.
引导学生对所学的知识、数学思想方法进行归纳小结.
(四)巩固练习:课本P46 练习1-2
(五)小结:(由学生小结,教师补充、规范)
本节课主要学习了通过“五点作图法”正确找出函数y=sin x到y=Asin x, y=sin(x+φ)和y=sinωx的图像变换规律,能够自主说明各函数的性质变化,体现了数形结合、化归的数学思想方法。
(六)作业:课本P46 练习1 3 课本P52 练习2 1
六、教学反思
本节课用简谐振动中的位移与时间的图像引入新课,创设情境,激发学生学习的兴趣;通过问题链的设置,让学生先动手用五点法作图,树立起数形结合的思想,然后利用电脑动态演示图像的变换过程,突破传统教学上的难点。通过实践练习,整个教学过程中,让学生动手探究,教师追问,每个知识都由学生通过活动、探究、体验来获得,使学生真正成为学习课程的主体。
(设计者:西安市第一中学 )
