新版冀教版2019秋八年级数学下册第十九章平面直角坐标系小结与复习教学课件(22张ppt)
文档属性
| 名称 | 新版冀教版2019秋八年级数学下册第十九章平面直角坐标系小结与复习教学课件(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1005.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 21:27:06 | ||
图片预览






文档简介
(共22张PPT)
小结与复习
第十九章 平面直角坐标系
要点梳理
考点讲练
课堂小结
课后作业
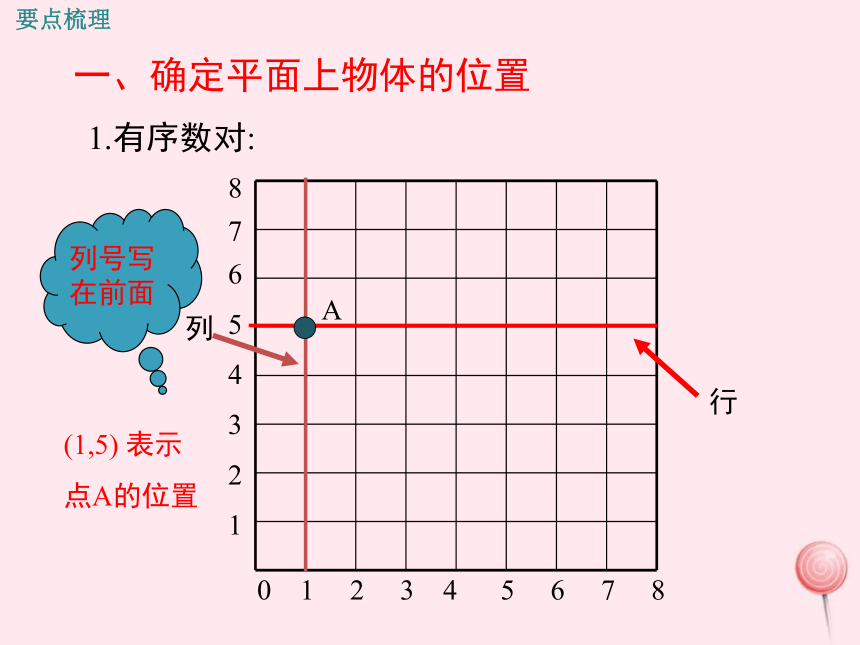
1.有序数对:
一、确定平面上物体的位置
0 1 2 3 4 5 6 7 8
(1,5) 表示点A的位置
A
列号写在前面
要点梳理
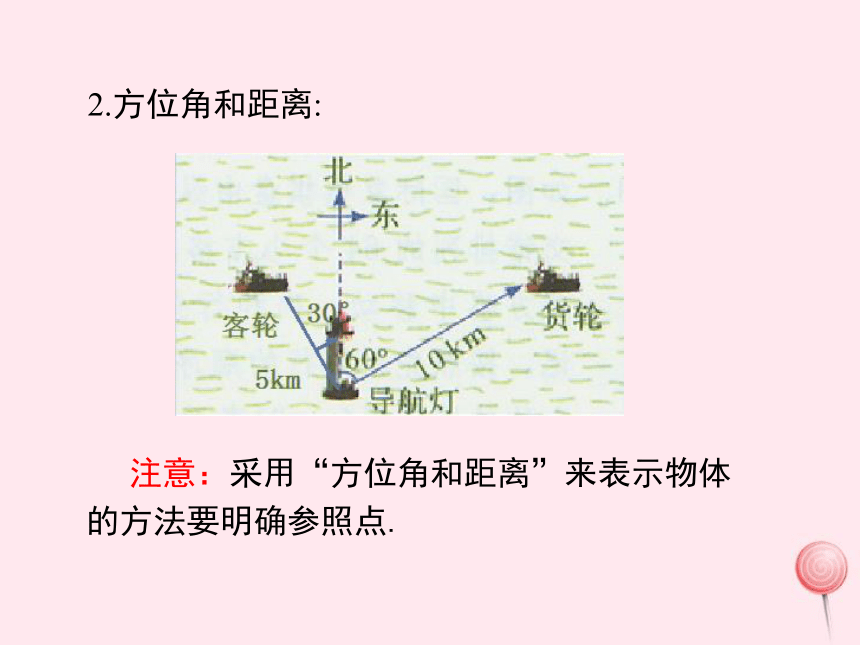
2.方位角和距离:
注意:采用“方位角和距离”来表示物体的方法要明确参照点.
1.平面直角坐标系
二、平面直角坐标系
2.各象限点的坐标的符号
(+,+)
(-,+)
(-,-)
(+,-)
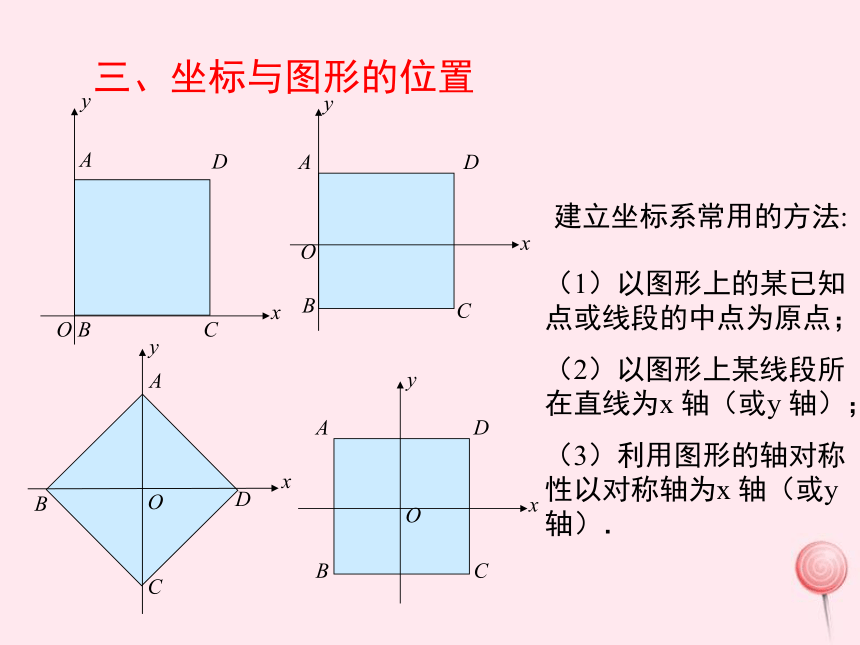
三、坐标与图形的位置
建立坐标系常用的方法:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x 轴(或y 轴);
(3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
四、坐标与图形的变化
1.图形的平移与坐标变化
(x,y) (x+a,y)
(x,y) (x-a,y)
(x,y) (x,y+a)
(x,y) (x,y-a)
向右平移a个单位
向左平移a个单位
向上平移a个单位
向下平移a个单位
关于x轴成对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数.
关于y轴成对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等.
2.图形的轴对称与坐标变化
特殊位置点的特殊坐标
关于y轴对称
关于x轴对称
平行于y轴
平行于x轴
原点
y轴
x轴
点P(x,y)对称点的坐标
连线平行于坐标轴的点
坐标轴上的点P(x,y)
(-x,y)
(x,-y)
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
(-x,-y)
关于原点对称
将一个图形各顶点的横坐标和纵坐标都乘以k(或 ,k>1),所得图形的形状 ,各边扩大为原来的 倍(或缩小为原来的 ),且连接各对应顶点的直线 .
不变
k
交于一点
3.图形的放缩与坐标变化
例1 .已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】由点P(0,m)在y轴的负半轴上,得m<0.
由不等式的性质,得-m>0,-m+1>1,
则点M(-m,-m+1)在第一象限,故选A.
A
考点讲练
1.已知点M(2+x,9-x2 )在x轴的负半轴上,则点M的坐标是 .
(-1,0)
2.已知点P(m+n-4,m-2)同时在两坐标轴上,则点Q(2m,-2n)的坐标为 .
(4,-4)
例2:如图是某公园景点的平面图(比例尺为1∶10000),请建立适当的平面直角坐标系,用坐标分别表示各建筑的位置.
解:如图,以广场为原点,正东方向为x轴正方向,正北方向为y轴正方向,建立平面直角坐标系.测量出碰碰车距广场的图上距离为1.5cm,根据比例尺实际距离为150m,以1m为一个单位长度,图中各地的坐标为广场(0,0),
打靶场(-150,75),
钓鱼台(-75,225),
碰碰车(0,150),
动物馆(75,225).
3.如图是丁丁画的一张脸的示意图,如果用(0,
2)表示靠左边的眼睛,用(2,2)表示靠右边
的眼睛,那么嘴的位置可以表示成( )
A.(1,0) B.(-1,0) C.(-1,1) D.(1,-1)
4.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
A.距点O4km处
B.北偏东40°方向上4km处
C.在点O北偏东50°方向上4km处
D.在点O北偏东40°方向上4km处
A
D
例3.如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A.(-2,-4) B.(-2,4)
C.(2,-3) D.(-1,-3)
【解析】由题意可知坐标变化规律是(x,y)→(x+2,y-3),照此规律计算可知顶点P(-4,-1)平移后的坐标是(-2,-4).故选A.
A
例4:(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A(0,2)
B(4,3)
C(3,0)
5.5
图形的平移变换,点的坐标变化规律是:右移横坐标加,左移减;上移纵坐标加,下移减.
5.三角形ABC中BC边上的中点为M,在把三角形ABC向左平移2个单位,再向上平移3个单位后,得到三角形A1B1C1的B1C1边上中点M1此时的坐标为(-1,0),则M点坐标为 .
(1,-3)
6.如图,把△ABC经过一定的变换得到△A′B′C′,
如果△ABC上点P的坐标为(a,b),那么点P变换
后的对应点P′的坐标为 .
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
例5.点P(1,-2)关于x轴的对称点是P1,P1关于y轴的对称点坐标是P2,则P2的坐标为( )
A.(1,-2) B.(-1,2)
C.(-1,-2) D.(-2,-1)
B
【解析】点P(1,-2)关于x轴的对称点是P1(1,2),P1关于y轴的对称点坐标P2的坐标为(-1,2),
7.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2017的值为( )
A.0 B.1 C.-1 D.(-3)2017
【解析】∵点P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,解得a=3,b=-4,
∴(a+b)2017=-1.
C
8.如图,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).
(1)在图中作出△ABC关于y轴对称的图△A1B1C1.
(2)写出点C1的坐标.
解:(1)如图所示:
(2)点C1的坐标为:(4,3).
课堂小结
确定平面上物体的位置
方位角和距离
坐标与图形的位置
点的坐标
平面直角坐标系
坐标与图形的变化
轴对称
平移
放缩
小结与复习
第十九章 平面直角坐标系
要点梳理
考点讲练
课堂小结
课后作业
1.有序数对:
一、确定平面上物体的位置
0 1 2 3 4 5 6 7 8
(1,5) 表示点A的位置
A
列号写在前面
要点梳理
2.方位角和距离:
注意:采用“方位角和距离”来表示物体的方法要明确参照点.
1.平面直角坐标系
二、平面直角坐标系
2.各象限点的坐标的符号
(+,+)
(-,+)
(-,-)
(+,-)
三、坐标与图形的位置
建立坐标系常用的方法:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x 轴(或y 轴);
(3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
四、坐标与图形的变化
1.图形的平移与坐标变化
(x,y) (x+a,y)
(x,y) (x-a,y)
(x,y) (x,y+a)
(x,y) (x,y-a)
向右平移a个单位
向左平移a个单位
向上平移a个单位
向下平移a个单位
关于x轴成对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数.
关于y轴成对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等.
2.图形的轴对称与坐标变化
特殊位置点的特殊坐标
关于y轴对称
关于x轴对称
平行于y轴
平行于x轴
原点
y轴
x轴
点P(x,y)对称点的坐标
连线平行于坐标轴的点
坐标轴上的点P(x,y)
(-x,y)
(x,-y)
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
(-x,-y)
关于原点对称
将一个图形各顶点的横坐标和纵坐标都乘以k(或 ,k>1),所得图形的形状 ,各边扩大为原来的 倍(或缩小为原来的 ),且连接各对应顶点的直线 .
不变
k
交于一点
3.图形的放缩与坐标变化
例1 .已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】由点P(0,m)在y轴的负半轴上,得m<0.
由不等式的性质,得-m>0,-m+1>1,
则点M(-m,-m+1)在第一象限,故选A.
A
考点讲练
1.已知点M(2+x,9-x2 )在x轴的负半轴上,则点M的坐标是 .
(-1,0)
2.已知点P(m+n-4,m-2)同时在两坐标轴上,则点Q(2m,-2n)的坐标为 .
(4,-4)
例2:如图是某公园景点的平面图(比例尺为1∶10000),请建立适当的平面直角坐标系,用坐标分别表示各建筑的位置.
解:如图,以广场为原点,正东方向为x轴正方向,正北方向为y轴正方向,建立平面直角坐标系.测量出碰碰车距广场的图上距离为1.5cm,根据比例尺实际距离为150m,以1m为一个单位长度,图中各地的坐标为广场(0,0),
打靶场(-150,75),
钓鱼台(-75,225),
碰碰车(0,150),
动物馆(75,225).
3.如图是丁丁画的一张脸的示意图,如果用(0,
2)表示靠左边的眼睛,用(2,2)表示靠右边
的眼睛,那么嘴的位置可以表示成( )
A.(1,0) B.(-1,0) C.(-1,1) D.(1,-1)
4.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
A.距点O4km处
B.北偏东40°方向上4km处
C.在点O北偏东50°方向上4km处
D.在点O北偏东40°方向上4km处
A
D
例3.如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A.(-2,-4) B.(-2,4)
C.(2,-3) D.(-1,-3)
【解析】由题意可知坐标变化规律是(x,y)→(x+2,y-3),照此规律计算可知顶点P(-4,-1)平移后的坐标是(-2,-4).故选A.
A
例4:(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A(0,2)
B(4,3)
C(3,0)
5.5
图形的平移变换,点的坐标变化规律是:右移横坐标加,左移减;上移纵坐标加,下移减.
5.三角形ABC中BC边上的中点为M,在把三角形ABC向左平移2个单位,再向上平移3个单位后,得到三角形A1B1C1的B1C1边上中点M1此时的坐标为(-1,0),则M点坐标为 .
(1,-3)
6.如图,把△ABC经过一定的变换得到△A′B′C′,
如果△ABC上点P的坐标为(a,b),那么点P变换
后的对应点P′的坐标为 .
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
例5.点P(1,-2)关于x轴的对称点是P1,P1关于y轴的对称点坐标是P2,则P2的坐标为( )
A.(1,-2) B.(-1,2)
C.(-1,-2) D.(-2,-1)
B
【解析】点P(1,-2)关于x轴的对称点是P1(1,2),P1关于y轴的对称点坐标P2的坐标为(-1,2),
7.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2017的值为( )
A.0 B.1 C.-1 D.(-3)2017
【解析】∵点P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,解得a=3,b=-4,
∴(a+b)2017=-1.
C
8.如图,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).
(1)在图中作出△ABC关于y轴对称的图△A1B1C1.
(2)写出点C1的坐标.
解:(1)如图所示:
(2)点C1的坐标为:(4,3).
课堂小结
确定平面上物体的位置
方位角和距离
坐标与图形的位置
点的坐标
平面直角坐标系
坐标与图形的变化
轴对称
平移
放缩
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
