人教版八年级数学下册19.3 课题学习 选择方案课件(共23张)
文档属性
| 名称 | 人教版八年级数学下册19.3 课题学习 选择方案课件(共23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 08:49:37 | ||
图片预览







文档简介
(共23张PPT)
19.3
课题学习
选择方案.
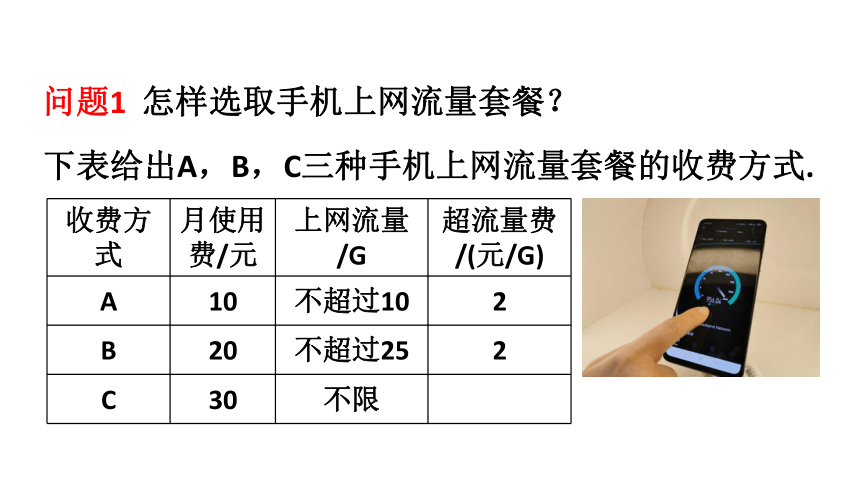
问题1
怎样选取手机上网流量套餐?
下表给出A,B,C三种手机上网流量套餐的收费方式.
收费方式
月使用费/元
上网流量/G
超流量费/(元/G)
A
10
不超过10
2
B
20
不超过25
2
C
30
不限
1.哪种手机上网流量费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,手机上网流量费由哪些部分组成?
手机上网流量费
=
月使用费
+
超流量费
3.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的流量有关
4.设月手机上网流量为x,则方式A、B的手机上网流量费y1、y2都是x的函数,要比较它们,需在
x
0
时,考虑何时
(1)
y1
=
y2;
(2)
y1
<
y2;
(3)
y1
>
y2.
5.在方式A中,超流量费一定会产生吗?什么情况下才会有超流量费?
不一定,只有在手机上网流量超过10G时才会产生.
合起来可写为:
当0≤x≤10时,y1=10;
当x>10时,y1=10+2×(x-10)=2x-10.
6.你能自己写出方式B的手机上网流量费y2关于手机上网流量
x之间的函数关系式吗
方式C的手机上网流量费y3关于手机上网流量x之间的
函数关系式呢
当x≥0时,y3=30.
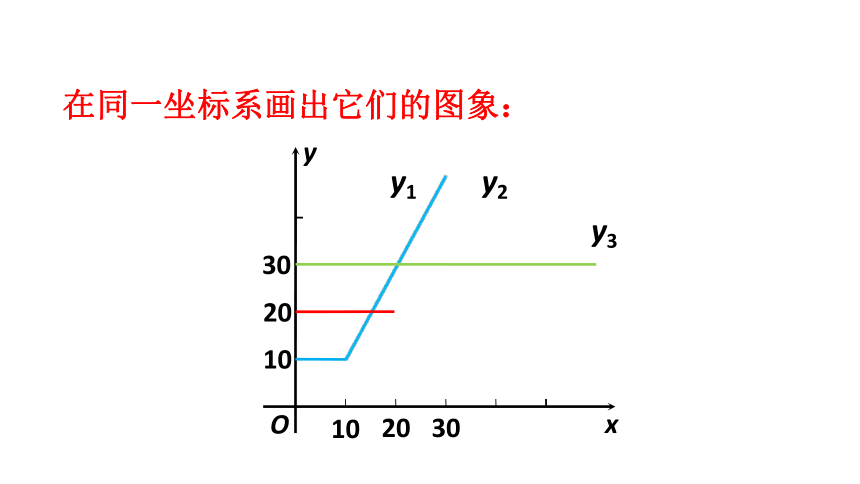
在同一坐标系画出它们的图象:
30
20
10
10
20
30
O
x
y
y1
y2
y3
7.当手机上网流量___________时,选择方式A最省钱.
当手机上网流量_________________时,选择方式B最省钱.
当手机上网流量___________时,选择方式C最省钱.
不超过15G
在15G-25G之间
超过25G
问题2
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
分析(1)影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
(2)汽车所租辆数又与哪些因素有关?
与乘车人数有关.
(3)如何由乘车人数确定租车辆数呢?
①要保证240
名师生都有车坐,汽车总数不能小于6
辆;
②要使每辆汽车上至少有1
名教师,汽车总数
不能大于6
辆.
(4)在汽车总数确定后,租车费用与租车的种类
有关.如果租甲类车x
辆,能求出租车费用吗?
设租用
x
辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;设租车费用为
y,则y
=400x+280(6-x)化简得y
=120x+1
680.
①为使240
名师生有车坐,则
45x+30(6-x)≥240;
②为使租车费用不超过2
300
元,则
400x+280(6-x)≤2
300.
(5)如何确定
y
=120x+1
680中
y
的最小值.
45x+30(6-x)≥240
400x+280(6-x)≤2
300
由 得4≤x≤
.
据实际意义可取4
或5;
因为
y
随着
x
的增大而增大,所以当
x
=4
时,y
最小,y
的最小值为2
160.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
归纳
抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
练习
广兴
50车
中山
50车
江津
60车
白沙
40车
(50-x)
(60-x)
x
650
500
700
600
(x-10)
解:设每天要从江津运x车到中山,总运费为y元.由题意可得
y=600x+700(60-x)+500(50
-x)+650(x-10)
y=50x+60500
由
得
∴
∵
k=50>0
y随x的增大而增大
∴当x=10时,y有最小值,
y=61000.
答:从江津调往中山10车,从江津调往广兴50车,从白沙调往中山40车,从白沙调往广兴0车,可使总费用最省,为61000元.
19.3
课题学习
选择方案.
问题1
怎样选取手机上网流量套餐?
下表给出A,B,C三种手机上网流量套餐的收费方式.
收费方式
月使用费/元
上网流量/G
超流量费/(元/G)
A
10
不超过10
2
B
20
不超过25
2
C
30
不限
1.哪种手机上网流量费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,手机上网流量费由哪些部分组成?
手机上网流量费
=
月使用费
+
超流量费
3.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的流量有关
4.设月手机上网流量为x,则方式A、B的手机上网流量费y1、y2都是x的函数,要比较它们,需在
x
0
时,考虑何时
(1)
y1
=
y2;
(2)
y1
<
y2;
(3)
y1
>
y2.
5.在方式A中,超流量费一定会产生吗?什么情况下才会有超流量费?
不一定,只有在手机上网流量超过10G时才会产生.
合起来可写为:
当0≤x≤10时,y1=10;
当x>10时,y1=10+2×(x-10)=2x-10.
6.你能自己写出方式B的手机上网流量费y2关于手机上网流量
x之间的函数关系式吗
方式C的手机上网流量费y3关于手机上网流量x之间的
函数关系式呢
当x≥0时,y3=30.
在同一坐标系画出它们的图象:
30
20
10
10
20
30
O
x
y
y1
y2
y3
7.当手机上网流量___________时,选择方式A最省钱.
当手机上网流量_________________时,选择方式B最省钱.
当手机上网流量___________时,选择方式C最省钱.
不超过15G
在15G-25G之间
超过25G
问题2
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
分析(1)影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
(2)汽车所租辆数又与哪些因素有关?
与乘车人数有关.
(3)如何由乘车人数确定租车辆数呢?
①要保证240
名师生都有车坐,汽车总数不能小于6
辆;
②要使每辆汽车上至少有1
名教师,汽车总数
不能大于6
辆.
(4)在汽车总数确定后,租车费用与租车的种类
有关.如果租甲类车x
辆,能求出租车费用吗?
设租用
x
辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;设租车费用为
y,则y
=400x+280(6-x)化简得y
=120x+1
680.
①为使240
名师生有车坐,则
45x+30(6-x)≥240;
②为使租车费用不超过2
300
元,则
400x+280(6-x)≤2
300.
(5)如何确定
y
=120x+1
680中
y
的最小值.
45x+30(6-x)≥240
400x+280(6-x)≤2
300
由 得4≤x≤
.
据实际意义可取4
或5;
因为
y
随着
x
的增大而增大,所以当
x
=4
时,y
最小,y
的最小值为2
160.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
归纳
抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
练习
广兴
50车
中山
50车
江津
60车
白沙
40车
(50-x)
(60-x)
x
650
500
700
600
(x-10)
解:设每天要从江津运x车到中山,总运费为y元.由题意可得
y=600x+700(60-x)+500(50
-x)+650(x-10)
y=50x+60500
由
得
∴
∵
k=50>0
y随x的增大而增大
∴当x=10时,y有最小值,
y=61000.
答:从江津调往中山10车,从江津调往广兴50车,从白沙调往中山40车,从白沙调往广兴0车,可使总费用最省,为61000元.
