鲁科版(2019)高中物理选修3-1. 带电粒子在磁场中的圆周运动同步检测试卷(下)
文档属性
| 名称 | 鲁科版(2019)高中物理选修3-1. 带电粒子在磁场中的圆周运动同步检测试卷(下) |  | |
| 格式 | zip | ||
| 文件大小 | 455.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-04 05:55:16 | ||
图片预览




文档简介
鲁科版(2019)高中物理选修3-1. 带电粒子在磁场中的圆周运动同步检测试卷(下)
[基础题]
1.空间存在方向垂直于纸面向里的匀强磁场,图中的正方形为其边界。一细束由两种粒子组成的粒子流沿垂直于磁场的方向从O点入射.这两种粒子带同种电荷,它们的电荷量、质量均不同,但其比荷相同,且都包含不同速率的粒子,不计重力。下列说法正确的是( )
A.入射速度不同的粒子在磁场中的运动时间一定不同
B.入射速度相同的粒子在磁场中的运动轨迹一定相同
C.在磁场中运动时间相同的粒子,其运动轨迹一定相同
D.在磁场中运动时间越长的粒子,其轨迹所对的圆心角一定越大
2.长为的水平极板间,有垂直纸面向里的匀强磁场,如图所示,磁感应强度为B,板间距离也为,板不带电,现有质量为m,电荷量为q的正电粒子(不计重力),从极板间左边中点处垂直磁感线以速度v水平射入磁场,欲使粒子不打在极板上,可采用的办法是 ( )
A.使粒子的速度
B.使粒子的速度
C.使粒子的速度
D.使粒子的速度
3.如图,一半径为R的圆形区域内有垂直于纸面向里的匀强磁场,一质量为m,电荷量为q的正电荷(重力忽略不计)以速度v沿正对着圆心O的方向射入磁场,从磁场中射出时速度方向改变了θ角.磁场的磁感应强度大小为( )
A. B.
C. D.
4.在同时存在匀强电场合匀强磁场的空间中取正交坐标系Oxyz(z轴正方向竖直向上),如图所示。已知电场方向沿z轴正方向,场强大小为E;磁场方向沿y轴正方向,磁感应强度的大小为B;重力加速度为g。问:一质量为m、带电量为+q的从原点出发的质点能否在坐标轴(x、y、z)上以速度v做匀速运动?若能,m、q、E、B、v及g应满足怎样的关系?若不能,说明理由.
答:能沿x周轴正向:Eq+Bqv=mg;能沿x周轴负向:Eq=mg+Bqv;
能沿y轴正向或负向:Eq=mg;
不能沿z轴,因为电场力和重力的合力沿z轴方向,洛伦兹力沿x轴方向,合力不可能为零.
5.如图所示,在圆心为O、半径为r的圆形区域内有方向垂直纸面向里的匀强磁场,一电子以速度v沿AO方向射入,后沿OB方向射出匀强磁场,若已知∠AOB=120°,则电子穿越此匀强磁场所经历的时间是多少?
解:由圆的性质可知,粒子的轨迹圆心只能在O点的正下方,画出粒子轨迹的示意图,如图所示,由几何关系可知圆心角为∠AO′B=60°,
粒子的轨迹半径为:R=rtan60°=r
故运动时间为:t====.
6.如图所示,半径为R的圆形区域内有垂直于纸面向里的匀强磁场,磁感应强度大小为B.若在圆心处静止的原子核中释放一个质量为m、电量为q的粒子,粒子的速度v0垂直于磁场,则初速度v0大小必须满足什么条件时,粒子才能从磁场中穿出,粒子穿过磁场需要的最长时间为多少?
v0>,
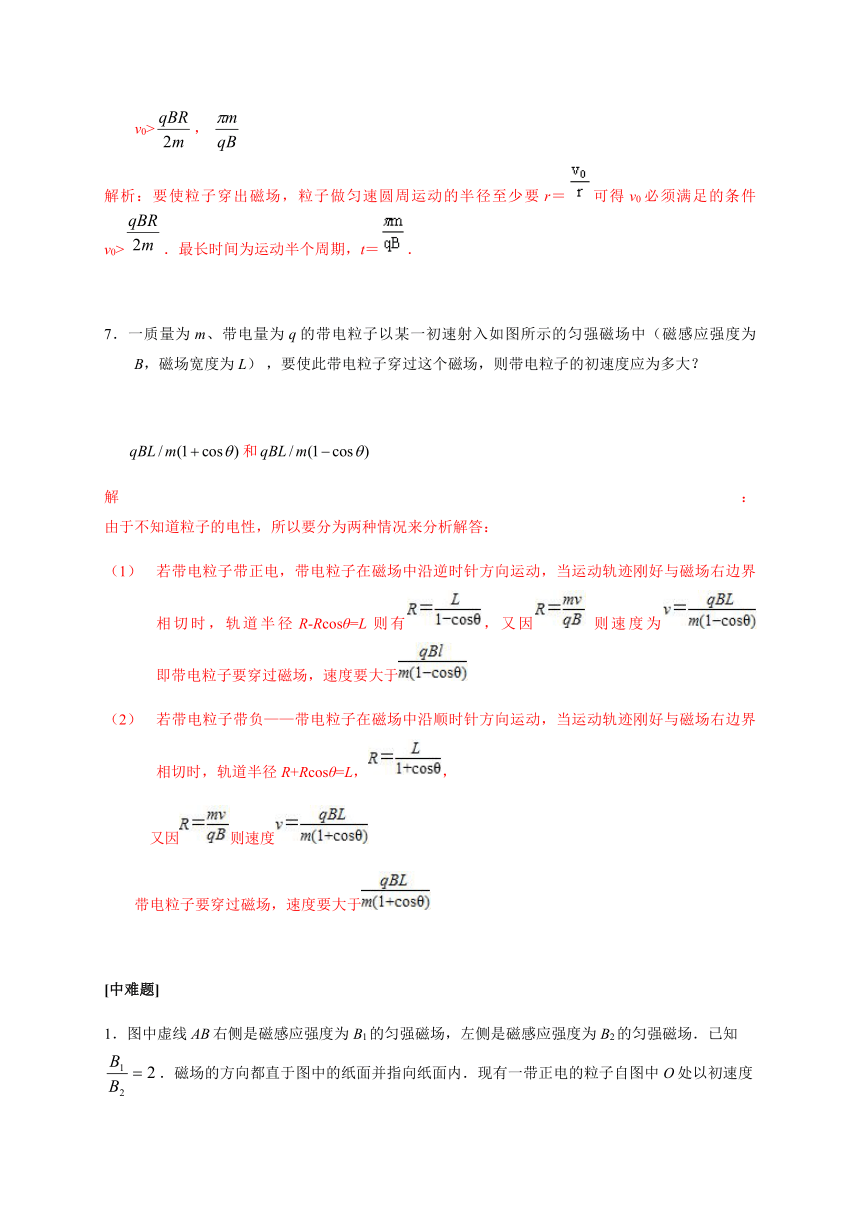
解析:要使粒子穿出磁场,粒子做匀速圆周运动的半径至少要r=可得v0必须满足的条件v0>.最长时间为运动半个周期,t=.
7.一质量为m、带电量为q的带电粒子以某一初速射入如图所示的匀强磁场中(磁感应强度为B,磁场宽度为L) ,要使此带电粒子穿过这个磁场,则带电粒子的初速度应为多大?
和
解:
由于不知道粒子的电性,所以要分为两种情况来分析解答:
(1) 若带电粒子带正电,带电粒子在磁场中沿逆时针方向运动,当运动轨迹刚好与磁场右边界相切时,轨道半径R-Rcosθ=L 则有,又因 则速度为
即带电粒子要穿过磁场,速度要大于
(2) 若带电粒子带负——带电粒子在磁场中沿顺时针方向运动,当运动轨迹刚好与磁场右边界相切时,轨道半径R+Rcosθ=L,,
又因则速度
带电粒子要穿过磁场,速度要大于
[中难题]
1.图中虚线AB右侧是磁感应强度为B1的匀强磁场,左侧是磁感应强度为B2的匀强磁场.已知.磁场的方向都直于图中的纸面并指向纸面内.现有一带正电的粒子自图中O处以初速度开始向右运动,求从开始时刻到第10次通过AB线向右运动的时间内,该粒子在AB方向的平均速度.
解析:R1=mv0/qB1 ?R2=mv0/qB2
?R2/R1=B1/B2=2
每转一圈q沿AB边下降距离L=2(R2-R1),
所用时间T=π(R2+R1)/v0
第10次通过AB时完成5圈,下降距离=5L
平均速度=5L/5T=2v0/3π
2.在以坐标原点 O为圆心、半径为 r的圆形区域内,存在磁感应强度大小为 B、方向垂直于纸面向里的匀强磁场,如图所示. 一个不计重力的带电粒子从磁场边界与 x轴的交点 A处以速度 v沿-x方向射入磁场,它恰好从磁场边界与 y轴的交点 C处沿+y方向飞出.
(1)请判断该粒子带何种电荷,并求出其比荷q/m ;
(2)若磁场的方向和所在空间范围不变,而磁感应强度的大小变为,该粒子仍从 A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了 60°角,求磁感应强度多大?此次粒子在磁场中运动所用时间 t是多少?
解析(1)由粒子的飞行轨迹,利用左手定则可知,该粒子带负电荷. 粒子由 A点射入,由 C点飞出,其速度方向改变了 90°,则粒子轨迹半径 又 ,则粒子的比荷
(2)粒子从 D 点飞出磁场速度方向改变了60°角,故 AD 弧所对圆心角 60°,粒子做圆周运动的半径 又 所以
粒子在磁场中飞行时间
3.如图,在一个圆形区域内,两个方向都垂直于纸面向外的匀强磁场分布在以直径24为边界的两个半圆形区域Ⅰ、Ⅱ中,直径24与13的夹角为60°,一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点1处沿与13成30°角的方向射入磁场,再以垂直24的方向经过圆心O进入Ⅱ区,最后再从2处射出磁场。已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度B1和B2的大小(忽略粒子重力).
【解析】粒子在Ⅰ区运动轨迹的圆心在2处,
由几何知识和题意可知,轨道半径R1=R,则 ①
轨迹所对应的圆心角
则运动时间 ②
粒子在Ⅱ区运动轨迹的圆心在O2的中点,由几何关系可知轨迹半径,
则 ③
轨迹对应的圆心角θ2=π,则运动时间 ④
由题意知: ⑤
由①③⑤式联立解得:
4.如图中虚线MN是一垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感应强度为B的匀强磁场,方向垂直纸面向外。O是MN上的一点,从O点可以向磁场区域发射电量为+q、质量为m、速率为v的粒子,粒子射入磁场时的速度可在纸面内各个方向。已知先后射入的两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L。不计重力及粒子间的相互作用。求:
(1)所考察的粒子在磁场中的轨道半径;
(2)这两个粒子从O点射人磁场的时间间隔。
解析:
(1)设粒子在磁场中做圆周运动的轨道半径为R,由牛顿第二定律得:qvB=mv2/R,??R=mv/qB????????????①
(2)以OP为弦画两个半径相等的圆弧,分别表示两个粒子的轨道.圆心和直径分别为O1、O2和OO1Q1、OO2Q2,在O处两个圆的切线分别表示两个粒子的射入方向,用θ表示它们之间的夹角,由几何关系得:∠PO1Q1=∠PO2Q2=θ?????????? ②
从O点射入到相遇,粒子1的路程为半个圆周加弧长Q1P,且Q1P=Rθ???????????????????????????? ????????③
粒子2的路程为半个圆周减弧长Q2P,且Q2P=Rθ?④
粒子1的运动时间为t1=T/2+Rθ/v??????????????⑤
?粒子2的运动时间为t1=T/2-Rθ/v????????? ?????⑥
两例子射入的时间间隔为△t=t1-t2=2Rθ/v??????????⑦
因Rcoc(θ/2)=L/2解得
θ=2Rarccos(L/2R)????????????????????????????? ⑧
由①⑦⑧三式解得:
[提高题]
1.如图所示为EAST部分装置的简化模型:垂直纸面的有环形边界的匀强磁场b区域,围着磁感应强度为零的圆形a区域,a区域内的离子向各个方向运动,离子的速度只要不超过某值,就不能穿过环形磁场的外边界而逃逸,从而被约束。设离子质量为m,电荷量为q,环形磁场的内半径为R1, 外半径R2 =(1+)R1。
(1)若要使从a区域沿任何方向,速率为v的离子射入磁场时都不能越出磁场的外边界,则b区域磁场的磁感应强度至少为多大?
(2)若b区域内磁场的磁感应强度为B,离子从a区域中心O点沿半径OM方向以某一速度射入b区,恰好不越出磁场的外边界。请画出在该情况下离子在a、b区域内运动一个周期的轨迹,并求出周期。
⑴当离子的速度沿与内边界圆相切的方向射入磁场,且轨道与磁场外圆相切时所需磁场的磁感应强度B1,即为要求的值。设轨迹圆的半径为r1,
则r1==(1分) 由:qvB1=m(1分)
解之得:B1=(2分)
⑵如图(2分)。要使沿OM方向运动的离子不能穿越磁场,则其在环形磁场内的运动轨迹圆中最大值与磁场外边界圆相切。设这时轨迹圆的半径为r2,速度为v2,则:
r22 +R12=(R2一r2)2 (1分) 解之得:r 2 =R1 (1分)
由qv2B=m 解之得:v2 = (1分)
离子在b区域中做匀速圆周运动的周期T1= (1分)
离子在b区域中一次运动的时间t1 = (1分)
离子在a区域中由O到M点的运动时间t2 = (1分)
离子在a、b区域内运动的周期T= 4t1+8t2 =(2分)
2、如图所示,两块垂直纸面的平行金属板A、B相距d=10.0 cm,B板的中央M处有一个α粒子源,可向各个方向射出速率相同的α粒子,α粒子的荷质比q/m=4.82×107 C/kg.为使所有α粒子都不能达到A板,可以在A、B板间加一个电压,所加电压最小值是U0=4.15×104 V;若撤去A、B间的电压,仍使所有α粒子都不能到达A板,可以在A、B间加一个垂直纸面的匀强磁场,该匀强磁场的磁感应强度B必须符合什么条件?
解:设速率为v,在电场力作用下最容易到达A板的是速
度方向垂直B板的粒子
由动能定理得:
加磁场后,只要速率为v的粒子轨迹与AB板都相切的粒子打不到板即可.此粒子的轨道半径为,与此对应的磁感应强度就是B的最小值.
因为:
由上两式得:?
即磁感应强度B应满足?
3、利用如图所示装置可以选择一定速度范围内的带电粒子。图中板MN上方是磁感应强度大小为B、方向垂直纸面向里的匀强磁场,板上有两条宽度分别为2d和d的缝,两缝近端相距为L,一群质量为m、电荷量为q,具有不同速度的粒子从宽度为2d的缝垂直于板MN进入磁场,对于能够从宽度为d的缝射出的粒子,求:粒子的最大速度与最小速度之差
粒子的最大半径,为
粒子的最小半径,为,
根据
可得、
则
4.如图19(a)所示,在以O为圆心,内外半径分别为和? B
b e Q a
F B
c f P d
?的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。
(1)已知粒子从外圆上以速度射出,求粒子在A点的初速度的大小
(2)若撤去电场,如图19(b),已知粒子从OA延长线与外圆的交点C以速度射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间
(3)在图19(b)中,若粒子从A点进入磁场,速度大小为,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?
(1) 带电粒子在复合场中受到电场力和洛伦兹力的作用,因为洛伦兹力不做功,故只要有电场力做功,由动能定理得:.
(2) 做出粒子运动的轨迹如图所示,则,得粒子的运动半径为
洛伦兹力提供向心力:,联立解得:
在磁场中的运动时间为:
(3)若粒子能够从AO延长线与外圆的交点射出,则有所有粒子均射出,此时粒子在A点的射入方向是垂直AC向下的,粒子轨迹的半径为,此时对应磁感应强度是最大的设为Bm,要使粒子能从外圆射出,由洛伦兹力提供向心力得:所以
5.如图所示的直角坐标系第、象限内存在方向向里的匀强磁场,磁感应强度大小B=0.5T,处于坐标原点O的放射源不断地放射出比荷C/kg的正离子,不计离子之间的相互作用。
⑴求离子在匀强磁场中运动周期;
⑵若某时刻一群离子自原点O以不同速率沿x轴正方向射出,求经过s时间这些离子所在位置构成的曲线方程;
⑶若离子自原点O以相同的速率v0=2.0×106m/s沿不同方向射入第象限,要求这些离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动,则题干中的匀强磁场区域应怎样调整(画图说明即可)?并求出调整后磁场区域的最小面积。
解:⑴根据牛顿第二定律??有 ???????????
??运动周期??????
⑵离子运动时间??????????????????????????????????????
根据左手定则,离子沿逆时针方向作半径不同的圆周运动,转过的角度均为??????
这些离子所在位置均在过坐标原点的同一条直线上,该直线方程???????????? ???????????????????
⑶离子自原点O以相同的速率v0沿不同方向射入第一象限磁场,均做逆时针方向的匀速圆周运动
根据牛顿第二定律??有???????
?? ?m?????
这些离子的轨道圆心均在第二象限的四分之一圆弧AC上,欲使离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动,离开磁场时的位置在以点(1,0)为圆心、半径R=1m的四分之一圆弧(从原点O起顺时针转动)上,磁场区域为两个四分之一圆的交集,如图所示????????????????????????????????
调整后磁场区域的最小面积m2 ???
a区域
O
M
R2
R1
b区域
B
同课章节目录
- 第1章 静电场
- 导入 神奇的静电
- 第1节 静电现象及其微观解释
- 第2节 静电力 库仑定律
- 第3节 电场及其描述
- 第4节 电场中的导体
- 第2章 电势能与电势差
- 导入 电场力可以做功吗
- 第1节 电场力做功与电势能
- 第2节 电势与等势面
- 第3节 电势差
- 第4节 电容器 电容
- 专题探究 电场部分专题探究示例
- 第3章 恒定电流
- 导入 历史的回眸
- 第1节 电流
- 第2节 电阻
- 第3节 焦耳定律
- 第4节 串联分压与并联分流
- 第4章 闭合电路欧姆定律和逻辑电路
- 导入 从闭合电路找原因
- 第1节 闭合电路欧姆定律
- 第2节 多用电表的原理与使用
- 第3节 测量电源的电功势和内电阻
- 第4节 逻辑电路与自动控制
- 专题探究 电路部分专题探究示例
- 第5章 磁场
- 导入 “迷路”的信鸽
- 第1节 磁场
- 第2节 用磁感线描述磁场
- 第3节 磁感应强度 磁通量
- 第4节 磁与现代科技
- 第6章 磁场对电流和运动电荷的作用
- 导入 从奥斯特实验说起
- 第1节 探究磁场对电流的作用
- 第2节 磁场对运动电荷的作用
- 第3节 洛仑兹力的应用
- 专题探究 磁场部分专题探究示例
