北师大版九年级下册数学:1.1.1 锐角三角函数教案
文档属性
| 名称 | 北师大版九年级下册数学:1.1.1 锐角三角函数教案 |  | |
| 格式 | zip | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 09:21:32 | ||
图片预览

文档简介
课题 1.1.1 锐角三角函数
学情分析 从学生的认知水平和能力状况来看,初三学生处于形象思维向抽象思维过渡的阶段。对历史的认识仍处在感性认识阶段,辩证看待历史问题的能力不强。因此,要通过各种情境资料和导学法来启发学生的思维,在教学中要增强直观性和趣味性,调动学生学习的积极性和主动性;通过让学生动口、动手、动脑,活跃思维,提高他们分析问题和认识问题的能力,并能在感性认识的基础上进行理性思考,形成较全面的历史观点
教学目标 1.理解正切的意义和与现实生活的联系.2.用正切进行简单的计算.
教学 重 点 能进行简单的计算.
难 点 理解正切的意义
教 学 过 程 二 次 备 课
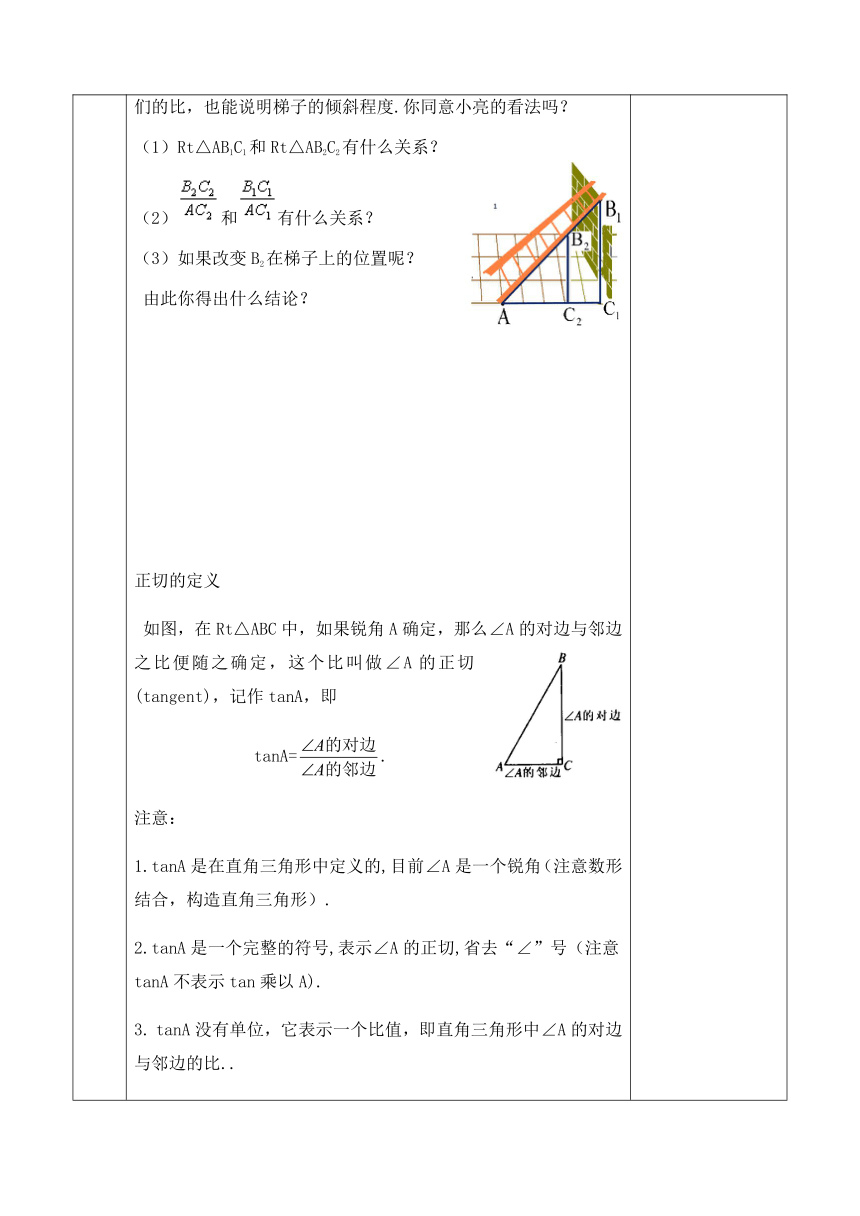
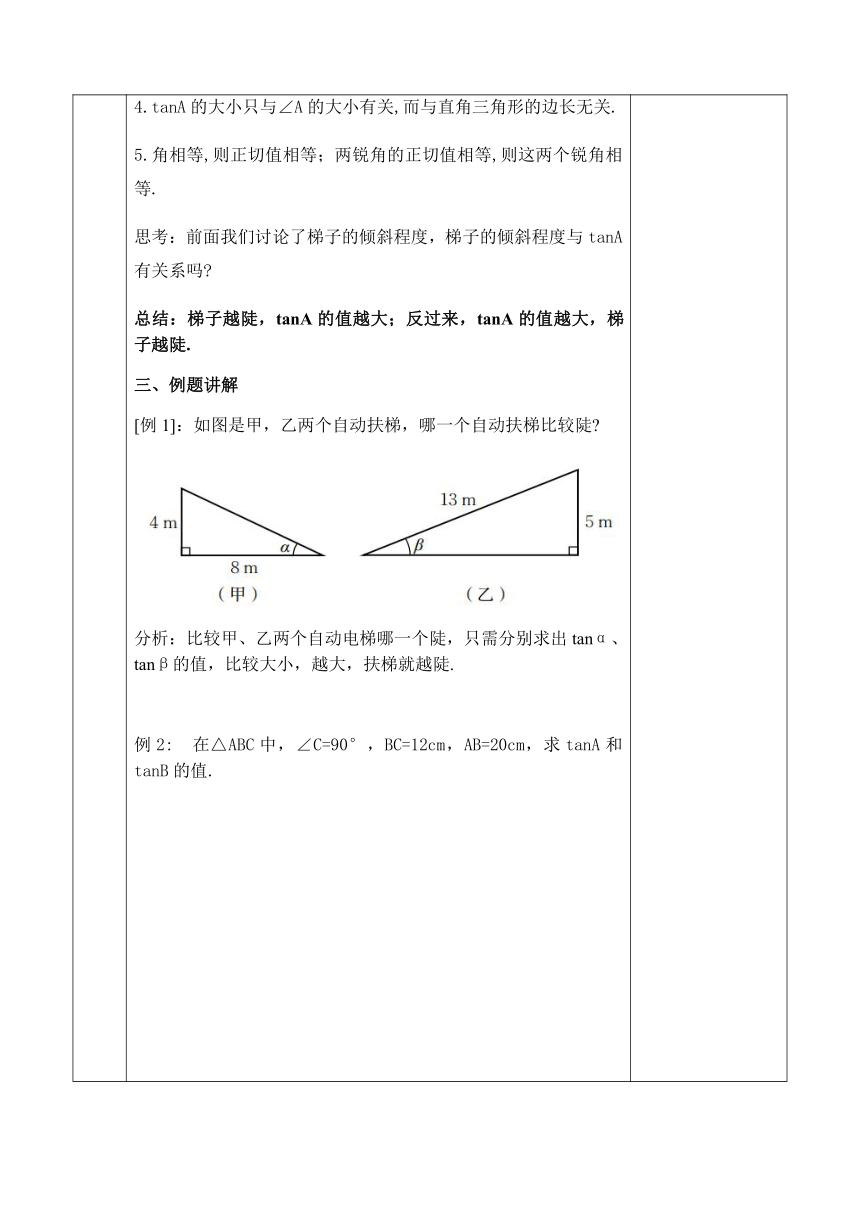
教 学 步 骤 一、创设问题情境,引入新课通过对课件封面图片的观察,提出问题:你会比较两个梯子哪个更陡吗?你有哪些办法?二、探究新知:活动一:图中,这里摆放的两个梯子,梯子AB和EF哪个更陡?你是怎样判断的?结论:当铅直高度一样,水平宽度越小,梯子越陡;当水平宽度一样,铅直高度越大,梯子越陡。活动二:如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为通过测量B2C2及AC2 ,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?(1)Rt△AB1C1和Rt△AB2C2有什么关系?(2)和有什么关系?(3)如果改变B2在梯子上的位置呢? 由此你得出什么结论? 正切的定义 如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边之比便随之确定,这个比叫做∠A的正切(tangent),记作tanA,即tanA=.注意:1.tanA是在直角三角形中定义的,目前∠A是一个锐角(注意数形结合,构造直角三角形).2.tanA是一个完整的符号,表示∠A的正切,省去“∠”号(注意tanA不表示tan乘以A).3. tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比..4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.思考:前面我们讨论了梯子的倾斜程度,梯子的倾斜程度与tanA有关系吗?总结:梯子越陡,tanA的值越大;反过来,tanA的值越大,梯子越陡.例题讲解[例1]:如图是甲,乙两个自动扶梯,哪一个自动扶梯比较陡?分析:比较甲、乙两个自动电梯哪一个陡,只需分别求出tanα、tanβ的值,比较大小,越大,扶梯就越陡.例2: 在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA和tanB的值. 四、坡度、坡角的定义坡度:斜坡、的铅直高度与水平宽度的比,也称为坡比(坡角的正切值就是坡度)如:山坡AB的坡角为∠A,坡度为tanA 五、随堂练习2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )A、扩大100倍 B、缩小100倍 C、不变 D、不能确定3.如图,△ABC中,AB=BC,则 tanC=( ).4. 在等腰△ABC中,AB=AC=13,BC=10,求tanB。 五、课堂小结通过本节课的学习,你有什么收获和体会?(学生小结,教师归纳)
作业 1、改错2、学习之友3、梳理概念
板书设计
教学反思
