北师大版八年级数学下册2.4 一元一次不等式课件(共27张)
文档属性
| 名称 | 北师大版八年级数学下册2.4 一元一次不等式课件(共27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 593.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览







文档简介
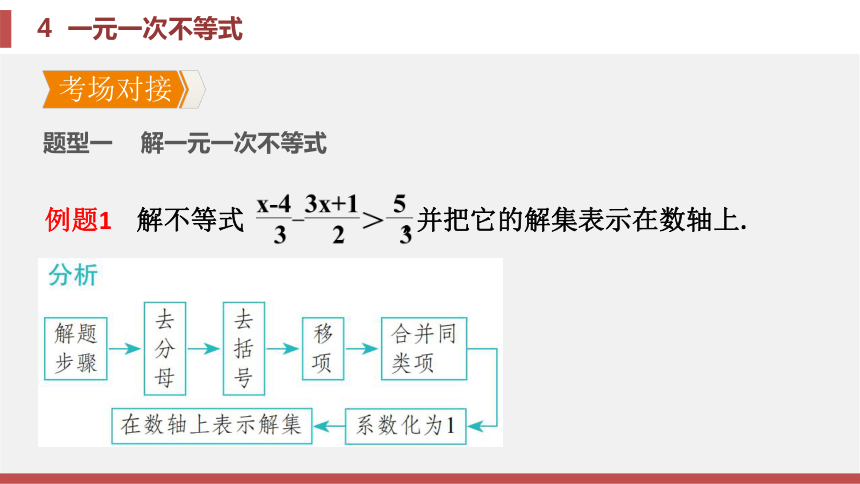
课件27张PPT。第二章 一元一次不等式与一元一次不等式组4 一元一次不等式第二章 一元一次不等式与一元一次不等式组4 一元一次不等式考场对接 题型一 解一元一次不等式锦囊妙计
解一元一次不等式的几点注意
(1)解不等式时应注意以下四个问题:
①去分母时, 每一项都要乘同一个数, 尤其不要漏乘常数项;
②移项时不要忘记变号;
③去括号时, 若括号外的因数是负号, 则括号里的每一项都要变号;
④在不等式两边都乘(或除以)同一个负数时, 不等号的方向要改变.
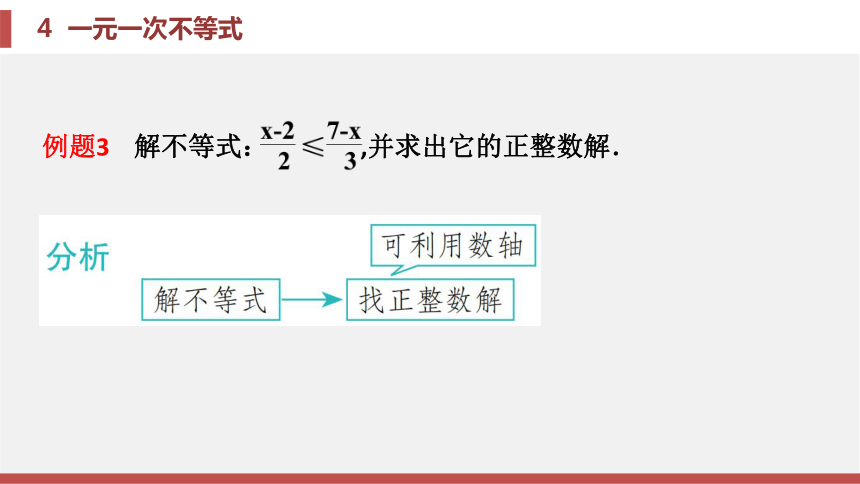
(2)在数轴上表示不等式的解集时, 大于向右, 小于向左, 有等号时画实心圆点, 没有等号时画空心圆圈.题型二 求一元一次不等式的特殊解例题2 [遵义中考] 不等式6-4x≥3x-8的非负整数解有( ).
A.2个 B.3个 C.4个 D.5个分析 移项, 得-4x-3x≥-8-6.
合并同类项, 得-7x≥-14.
两边都除以-7, 得x≤2.
故其非负整数解为0, 1, 2, 共3个.
故选B.B锦囊妙计
数形结合求特殊解
求不等式的特殊解的方法是先求出不等式的解集, 然后借助数轴确定其特殊解.题型三 已知不等式的解集求字母的值分析 去分母, 得x-m>9-3m.
移项、合并同类项, 得x>9-2m.
∵不等式的解集为x>1,
∴9-2m=1, 解得m=4. 4锦囊妙计
已知不等式的解集求字母值的方法
先表示出不等式的解集, 再根据已知条件列出关于所求字母的方程, 求解即可.题型四 解含字母的一元一次不等式例题5 若关于x的不等式3x-2<4x+1与2x-a>x+a的解集相同, 求a的值.分析 本题需要先解两个不等式, 然后通过对比解集求出a的值.锦囊妙计
解含字母的一元一次不等式的策略
解含字母的一元一次不等式时, 首先要分清哪些字母表示未知数, 哪些字母表示常数, 然后把不是未知数的字母当作常数按照解不等式的步骤求解. 解不等式时, 若题目中对表示常数的字母没有条件限制, 则必须对此字母所表示的数值针对不同的情形分类讨论.题型五 一元一次不等式的应用分析 设该用户2月份的用水量是x m3, 根据总费用不少于25元, 列出不等式求解.解 设该用户2月份的用水量是x m3.
因为1.5×10=15(元)<25元,
所以x>10.
由题意, 得1.5×10+2(x-10)≥25,
解得x≥15.
所以, 该用户2月份的用水量至少是15 m3.例题7 [泰安中考]某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克, 大樱桃每千克的进价比小樱桃每千克的进价多20元. 大樱桃的售价为每千克40元, 小樱桃的售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后, 该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克, 进价不变, 但在运输过程中小樱桃损耗了20%. 若小樱桃的售价不变, 要想让第二次赚的钱不少于第一次所赚钱的90%, 大樱桃的售价每千克最少应为多少?(2)设大樱桃的售价为每千克a元. 由题意, 得
(1-20%)×200×16+200a-8000≥3200×90%, 解得a≥41.6,
∴大樱桃的售价每千克最少应为41.6元. 锦囊妙计
用不等式解决实际问题的方法
用不等式解决实际问题的关键是找出问题中的不等关系, 设出未知数后, 根据不等关系列出不等式.通过解不等式求出解集, 结合实际意义确定实际问题的答案.题型六 不等式与方程(组)的综合应用分析 先解关于x, y的方程组, 用含a的代数式表示出x, y, 再代入不等式2x-y>1中即可求出a的取值范围.锦囊妙计
解不等式与方程(组)综合题的策略
先将方程(组)的解用含字母系数的代数式表示出来, 再根据题意列出不等式.
谢 谢 观 看!
解一元一次不等式的几点注意
(1)解不等式时应注意以下四个问题:
①去分母时, 每一项都要乘同一个数, 尤其不要漏乘常数项;
②移项时不要忘记变号;
③去括号时, 若括号外的因数是负号, 则括号里的每一项都要变号;
④在不等式两边都乘(或除以)同一个负数时, 不等号的方向要改变.
(2)在数轴上表示不等式的解集时, 大于向右, 小于向左, 有等号时画实心圆点, 没有等号时画空心圆圈.题型二 求一元一次不等式的特殊解例题2 [遵义中考] 不等式6-4x≥3x-8的非负整数解有( ).
A.2个 B.3个 C.4个 D.5个分析 移项, 得-4x-3x≥-8-6.
合并同类项, 得-7x≥-14.
两边都除以-7, 得x≤2.
故其非负整数解为0, 1, 2, 共3个.
故选B.B锦囊妙计
数形结合求特殊解
求不等式的特殊解的方法是先求出不等式的解集, 然后借助数轴确定其特殊解.题型三 已知不等式的解集求字母的值分析 去分母, 得x-m>9-3m.
移项、合并同类项, 得x>9-2m.
∵不等式的解集为x>1,
∴9-2m=1, 解得m=4. 4锦囊妙计
已知不等式的解集求字母值的方法
先表示出不等式的解集, 再根据已知条件列出关于所求字母的方程, 求解即可.题型四 解含字母的一元一次不等式例题5 若关于x的不等式3x-2<4x+1与2x-a>x+a的解集相同, 求a的值.分析 本题需要先解两个不等式, 然后通过对比解集求出a的值.锦囊妙计
解含字母的一元一次不等式的策略
解含字母的一元一次不等式时, 首先要分清哪些字母表示未知数, 哪些字母表示常数, 然后把不是未知数的字母当作常数按照解不等式的步骤求解. 解不等式时, 若题目中对表示常数的字母没有条件限制, 则必须对此字母所表示的数值针对不同的情形分类讨论.题型五 一元一次不等式的应用分析 设该用户2月份的用水量是x m3, 根据总费用不少于25元, 列出不等式求解.解 设该用户2月份的用水量是x m3.
因为1.5×10=15(元)<25元,
所以x>10.
由题意, 得1.5×10+2(x-10)≥25,
解得x≥15.
所以, 该用户2月份的用水量至少是15 m3.例题7 [泰安中考]某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克, 大樱桃每千克的进价比小樱桃每千克的进价多20元. 大樱桃的售价为每千克40元, 小樱桃的售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后, 该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克, 进价不变, 但在运输过程中小樱桃损耗了20%. 若小樱桃的售价不变, 要想让第二次赚的钱不少于第一次所赚钱的90%, 大樱桃的售价每千克最少应为多少?(2)设大樱桃的售价为每千克a元. 由题意, 得
(1-20%)×200×16+200a-8000≥3200×90%, 解得a≥41.6,
∴大樱桃的售价每千克最少应为41.6元. 锦囊妙计
用不等式解决实际问题的方法
用不等式解决实际问题的关键是找出问题中的不等关系, 设出未知数后, 根据不等关系列出不等式.通过解不等式求出解集, 结合实际意义确定实际问题的答案.题型六 不等式与方程(组)的综合应用分析 先解关于x, y的方程组, 用含a的代数式表示出x, y, 再代入不等式2x-y>1中即可求出a的取值范围.锦囊妙计
解不等式与方程(组)综合题的策略
先将方程(组)的解用含字母系数的代数式表示出来, 再根据题意列出不等式.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
