北师大版八年级数学下册6. 2 平行四边形的判定课件(共28张)
文档属性
| 名称 | 北师大版八年级数学下册6. 2 平行四边形的判定课件(共28张) |  | |
| 格式 | zip | ||
| 文件大小 | 687.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 11:59:14 | ||
图片预览







文档简介
课件28张PPT。第六章 平行四边形2 平行四边形的判定
第六章 平行四边形
2 平行四边形的判定
考场对接 题型一 平行四边形的判定
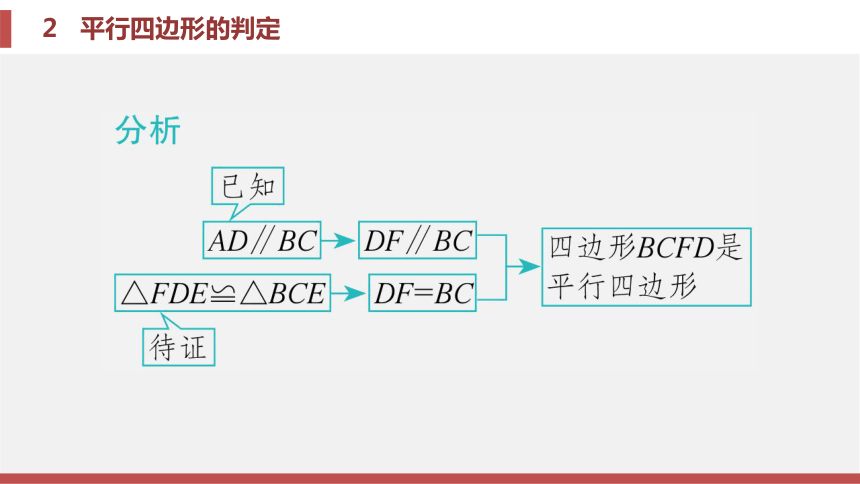
考场对接 例题1 已知:如图 6 - 2 - 16 , 在四边形 ABCD 中 , AD ∥ BC,E 是 CD 的中点 . BE 的延长线与 AD 的延长线相交于点 F, 连接 BD, CF. 判断四边形 BCFD 的
形状 , 并证明你的结论 .
解 四边形 BCFD 是平行四边形 . 证明:因为 E 是 CD 的中点 , 所以 DE = CE. 又因为 AD ∥ BC, 点 F 在 AD 的延长线上 , 所以 ∠ DFE =∠ CBE, ∠ FDE =∠ BCE. 在 △ FDE 与 △ BCE 中 , ∵ ∠ DFE =∠ CBE, ∠ FDE =∠ BCE, DE = CE, 所以 △ FDE ≌ △ BCE ( AAS ) , 所以 DF = BC. 又因为 DF ∥ BC, 所以四边形 BCFD 是平行四边形 .
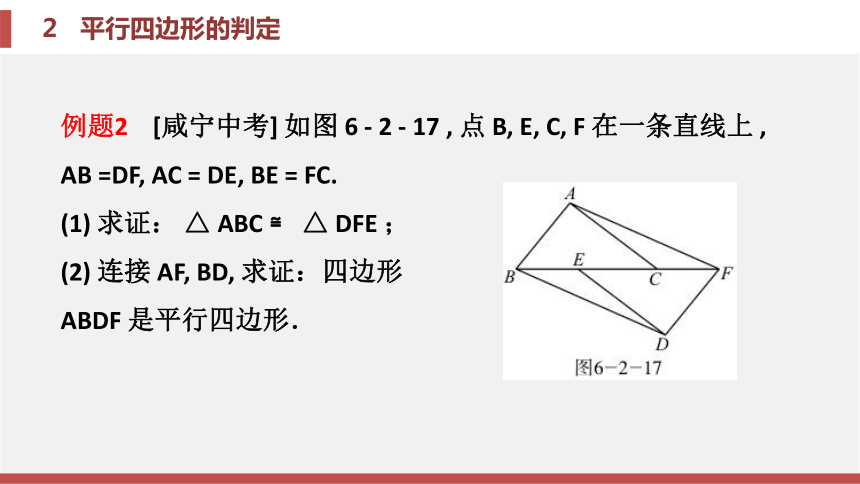
例题2 [咸宁中考] 如图 6 - 2 - 17 , 点 B, E, C, F 在一条直线上 , AB =DF, AC = DE, BE = FC.
(1) 求证: △ ABC ≌ △ DFE ; (2) 连接 AF, BD, 求证:四边形
ABDF 是平行四边形.
解 (1) 证明: ∵ BE = FC, ∴ BC = FE. 在 △ ABC 和 △ DFE 中 , ∵ AB = DF, AC = DE, BC = FE, ∴△ ABC ≌ △ DFE (SSS) . (2) 由 (1) 知 △ ABC ≌ △ DFE, ∴∠ ABC =∠ DFE, ∴ AB ∥ DF. 又 ∵ AB = DF, ∴ 四边形 ABDF 是平行四边形 . 锦囊妙计
巧选判定妙解问题
题型二 平行四边形判定的开放型题 例题3 在四边形 ABCD 中 , 已知 AD ∥ BC, 若再添加一个条件 , 能使四边形 ABCD 成为平行四边形 , 则这个条件可以 是______
____________________( 写出一个条件即可 , 不再添加辅助线 ) . 分析 平行添加条件 AD = BC, 可得出该四边形是平行四边形 .
∵ AD ∥ BC, AD = BC, ∴ 四边形 ABCD 是平行四边形 ( 一组对边平行且相等的四边形是平行四边形 ) . AD = BC ( 答案不唯一 )锦囊妙计
添加条件判定平行四边形
开放型题的解题关键是要突破思维定式的障碍 , 发散思维 , 多方面思考 , 探究问题在不同 条件下的不同 结论 , 挖掘它的内 在联系 , 向“纵、横、深、广”拓展 , 从而找出添加的条件和所得的结论 . 题型三 平行四边形的性质定理与判定定理的综合运用 解 (1) 证明: ∵ AC ⊥ BD, ∠ FCA = 90 ° ,
∴ BD ∥ CF.
∵∠ CBF =∠ DCB, ∴ CD ∥ BF,
∴ 四边形 DBFC 是平行四边形 . (2) ∵ 四边形 DBFC 是平行四边形 , ∴ CF = BD = 2 . ∵ AB = BC, AC ⊥ BD, ∴ AE = CE. 如图 , 过点 C 作 CM ⊥ BF 于点 M. ∵ BC 平分 ∠ DBF, ∴ CE = CM. ∵∠ F = 45 ° ,
∴△ CFM 是等腰直角三角形 , 从而 CM2 + MF2= 2 CM2=CF2, ∴ CM = CF = ,
∴ AE = CE = , ∴ AC = 2 . 锦囊妙计
平行四边形的性质与判定的综合应用策略
平行四边形具有对边平行且相等、对角相等、对角线互相平分等性质, 这些性质为我们证明线段平行、线段相等、角相等、两线段互相平分提供了新方法 . 在证明这些问题时 , 可依据平行四边形的判定方法 , 先判定与所求线段或角有关的四边形是平行四边形 , 再运用平行 四边形的性质解决问题 . 题型四 构造平行四边形解题 例题5 如图 6 - 2 - 19 , 已知 AB = AC, B 是 AD 的中点 , E 是 AB 的中点 .
求证: CD = 2 CE . 证明 如图 , 延长 CE至点 F, 使 EF = CE, 连接 AF, BF.
又 ∵ E 是 AB 的中点 , ∴ 四边形 AFBC 是平行四边形 , ∴ AC ∥ BF, AC = BF 又 ∵ AB = AC = BD, ∴ BD = BF, ∠ ABC =∠ ACB. ∵ AC ∥ BF, ∴∠ ACB +∠ CBF = 180 °. ∵∠ CBD +∠ ABC = 180 °, ∴∠ CBF =∠ CBD. 又 ∵ BC = BC, ∴△ BCD ≌ △ BCF, ∴ CD = CF = 2 CE . 锦囊妙计
构造平行四边形巧解问题
当题中有三角形的中线时 , 可以延长中线到原来的 2 倍构造平行四边形 , 然后利用平行四边形的性质推出线段相等、线段平行或角相等 . 题型五 与平行线之间的距离有关的计算题 例题6 如 图 6 - 2 - 20 , 已知 ABCD 的周长是 36 cm , 从钝角顶点 D 分别向AB, BC 引两条高 DE, DF, 且DE = 4 3 cm , DF = 5 3 cm , 求这个平行四边形的面积 . 锦囊妙计
列方程 ( 组 ) 巧解平行四边形面积问题
在计算题中经常用到平行四边形对边相等的关系和面积公式 , 应用面积公式时要注意高和底的对应关系 . 在涉及平行四边形的线段及面积的计算问题时 , 常构造直角三角形 , 从而借助勾股定理或等积法列方程或方程组进行解决 .
题型六 利用平行四边形的判定和性质解决动点问题 例题7 如 图 6 - 2 - 21 , 在四边形 ABCD 中 , AD ∥ BC, 且 AD > BC, BC = 6 cm , 点 P, Q 分别从点 A, C同
时出发 , 点 P 以 1 cm/s 的速度由点 A 向点 D
运动 , 点 Q 以 2 cm/s 的速度由点 C 向点 B运
动 . 当其中一点到达终点时 , 另一点随之停止
运动 . 几秒后四边形 BQP 是平行四边形?解 ∵ AD ∥ BC, ∴ AP ∥ BQ. 只有当 AP = BQ 时 , 四边形 ABQP 是平行四边形 . 设 t 秒后四边形 ABQP 是平行四边形 , 此时 , AP = t, BQ = 6 - 2 t, ∴ t = 6 - 2 t, 解得 t = 2 . 即 2 s 后四边形 ABQP 是平行四边形 . 锦囊妙计
解决平行四边形动点问题的策略
解决这类问题的一般思路是假设结论成立 ,反过来求所需要的条件 . 此类题一般会用到方程思想 .
谢 谢 观 看!
第六章 平行四边形
2 平行四边形的判定
考场对接 题型一 平行四边形的判定
考场对接 例题1 已知:如图 6 - 2 - 16 , 在四边形 ABCD 中 , AD ∥ BC,E 是 CD 的中点 . BE 的延长线与 AD 的延长线相交于点 F, 连接 BD, CF. 判断四边形 BCFD 的
形状 , 并证明你的结论 .
解 四边形 BCFD 是平行四边形 . 证明:因为 E 是 CD 的中点 , 所以 DE = CE. 又因为 AD ∥ BC, 点 F 在 AD 的延长线上 , 所以 ∠ DFE =∠ CBE, ∠ FDE =∠ BCE. 在 △ FDE 与 △ BCE 中 , ∵ ∠ DFE =∠ CBE, ∠ FDE =∠ BCE, DE = CE, 所以 △ FDE ≌ △ BCE ( AAS ) , 所以 DF = BC. 又因为 DF ∥ BC, 所以四边形 BCFD 是平行四边形 .
例题2 [咸宁中考] 如图 6 - 2 - 17 , 点 B, E, C, F 在一条直线上 , AB =DF, AC = DE, BE = FC.
(1) 求证: △ ABC ≌ △ DFE ; (2) 连接 AF, BD, 求证:四边形
ABDF 是平行四边形.
解 (1) 证明: ∵ BE = FC, ∴ BC = FE. 在 △ ABC 和 △ DFE 中 , ∵ AB = DF, AC = DE, BC = FE, ∴△ ABC ≌ △ DFE (SSS) . (2) 由 (1) 知 △ ABC ≌ △ DFE, ∴∠ ABC =∠ DFE, ∴ AB ∥ DF. 又 ∵ AB = DF, ∴ 四边形 ABDF 是平行四边形 . 锦囊妙计
巧选判定妙解问题
题型二 平行四边形判定的开放型题 例题3 在四边形 ABCD 中 , 已知 AD ∥ BC, 若再添加一个条件 , 能使四边形 ABCD 成为平行四边形 , 则这个条件可以 是______
____________________( 写出一个条件即可 , 不再添加辅助线 ) . 分析 平行添加条件 AD = BC, 可得出该四边形是平行四边形 .
∵ AD ∥ BC, AD = BC, ∴ 四边形 ABCD 是平行四边形 ( 一组对边平行且相等的四边形是平行四边形 ) . AD = BC ( 答案不唯一 )锦囊妙计
添加条件判定平行四边形
开放型题的解题关键是要突破思维定式的障碍 , 发散思维 , 多方面思考 , 探究问题在不同 条件下的不同 结论 , 挖掘它的内 在联系 , 向“纵、横、深、广”拓展 , 从而找出添加的条件和所得的结论 . 题型三 平行四边形的性质定理与判定定理的综合运用 解 (1) 证明: ∵ AC ⊥ BD, ∠ FCA = 90 ° ,
∴ BD ∥ CF.
∵∠ CBF =∠ DCB, ∴ CD ∥ BF,
∴ 四边形 DBFC 是平行四边形 . (2) ∵ 四边形 DBFC 是平行四边形 , ∴ CF = BD = 2 . ∵ AB = BC, AC ⊥ BD, ∴ AE = CE. 如图 , 过点 C 作 CM ⊥ BF 于点 M. ∵ BC 平分 ∠ DBF, ∴ CE = CM. ∵∠ F = 45 ° ,
∴△ CFM 是等腰直角三角形 , 从而 CM2 + MF2= 2 CM2=CF2, ∴ CM = CF = ,
∴ AE = CE = , ∴ AC = 2 . 锦囊妙计
平行四边形的性质与判定的综合应用策略
平行四边形具有对边平行且相等、对角相等、对角线互相平分等性质, 这些性质为我们证明线段平行、线段相等、角相等、两线段互相平分提供了新方法 . 在证明这些问题时 , 可依据平行四边形的判定方法 , 先判定与所求线段或角有关的四边形是平行四边形 , 再运用平行 四边形的性质解决问题 . 题型四 构造平行四边形解题 例题5 如图 6 - 2 - 19 , 已知 AB = AC, B 是 AD 的中点 , E 是 AB 的中点 .
求证: CD = 2 CE . 证明 如图 , 延长 CE至点 F, 使 EF = CE, 连接 AF, BF.
又 ∵ E 是 AB 的中点 , ∴ 四边形 AFBC 是平行四边形 , ∴ AC ∥ BF, AC = BF 又 ∵ AB = AC = BD, ∴ BD = BF, ∠ ABC =∠ ACB. ∵ AC ∥ BF, ∴∠ ACB +∠ CBF = 180 °. ∵∠ CBD +∠ ABC = 180 °, ∴∠ CBF =∠ CBD. 又 ∵ BC = BC, ∴△ BCD ≌ △ BCF, ∴ CD = CF = 2 CE . 锦囊妙计
构造平行四边形巧解问题
当题中有三角形的中线时 , 可以延长中线到原来的 2 倍构造平行四边形 , 然后利用平行四边形的性质推出线段相等、线段平行或角相等 . 题型五 与平行线之间的距离有关的计算题 例题6 如 图 6 - 2 - 20 , 已知 ABCD 的周长是 36 cm , 从钝角顶点 D 分别向AB, BC 引两条高 DE, DF, 且DE = 4 3 cm , DF = 5 3 cm , 求这个平行四边形的面积 . 锦囊妙计
列方程 ( 组 ) 巧解平行四边形面积问题
在计算题中经常用到平行四边形对边相等的关系和面积公式 , 应用面积公式时要注意高和底的对应关系 . 在涉及平行四边形的线段及面积的计算问题时 , 常构造直角三角形 , 从而借助勾股定理或等积法列方程或方程组进行解决 .
题型六 利用平行四边形的判定和性质解决动点问题 例题7 如 图 6 - 2 - 21 , 在四边形 ABCD 中 , AD ∥ BC, 且 AD > BC, BC = 6 cm , 点 P, Q 分别从点 A, C同
时出发 , 点 P 以 1 cm/s 的速度由点 A 向点 D
运动 , 点 Q 以 2 cm/s 的速度由点 C 向点 B运
动 . 当其中一点到达终点时 , 另一点随之停止
运动 . 几秒后四边形 BQP 是平行四边形?解 ∵ AD ∥ BC, ∴ AP ∥ BQ. 只有当 AP = BQ 时 , 四边形 ABQP 是平行四边形 . 设 t 秒后四边形 ABQP 是平行四边形 , 此时 , AP = t, BQ = 6 - 2 t, ∴ t = 6 - 2 t, 解得 t = 2 . 即 2 s 后四边形 ABQP 是平行四边形 . 锦囊妙计
解决平行四边形动点问题的策略
解决这类问题的一般思路是假设结论成立 ,反过来求所需要的条件 . 此类题一般会用到方程思想 .
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
