北师大版 八年级数学下册5.4 分式方程课件(共27张)
文档属性
| 名称 | 北师大版 八年级数学下册5.4 分式方程课件(共27张) |  | |
| 格式 | zip | ||
| 文件大小 | 781.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 12:50:35 | ||
图片预览







文档简介
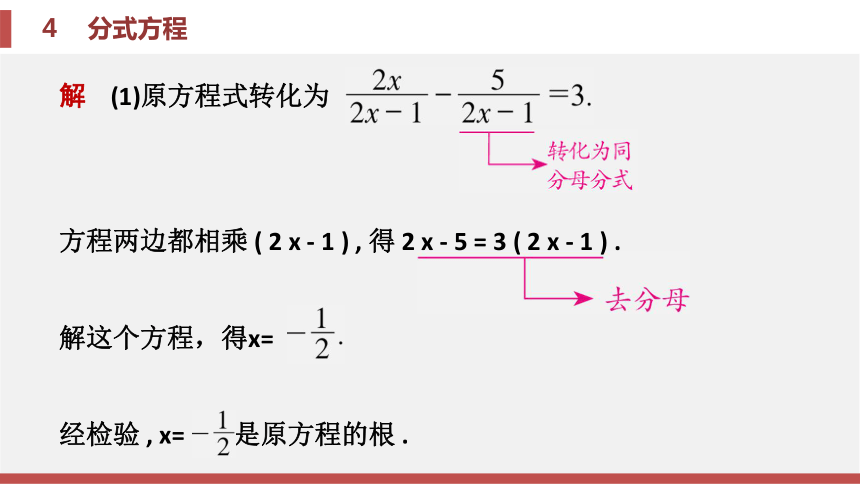
课件27张PPT。第五章 分式与分式方程4 分式方程第五章 分式与分式方程4 分式方程 考场对接 题型一 解分式方程 考场对接 例题1 解分式方程: 解 (1)原方程式转化为
方程两边都相乘 ( 2 x - 1 ) , 得 2 x - 5 = 3 ( 2 x - 1 ) .
解这个方程,得x=
经检验 , x= 是原方程的根 .方程两边都乘 x ( x + 1 ) , 得 5 x + 2 = 3 x. 解这个方程 , 得 x =- 1 . 检验:当 x =- 1 时 , x ( x + 1 ) =- 1 × ( - 1 + 1 ) = 0 . 所以 x =- 1 是原分式方程的增根 , 所以原方程无解 . 锦囊妙计
解分式方程的三个步骤
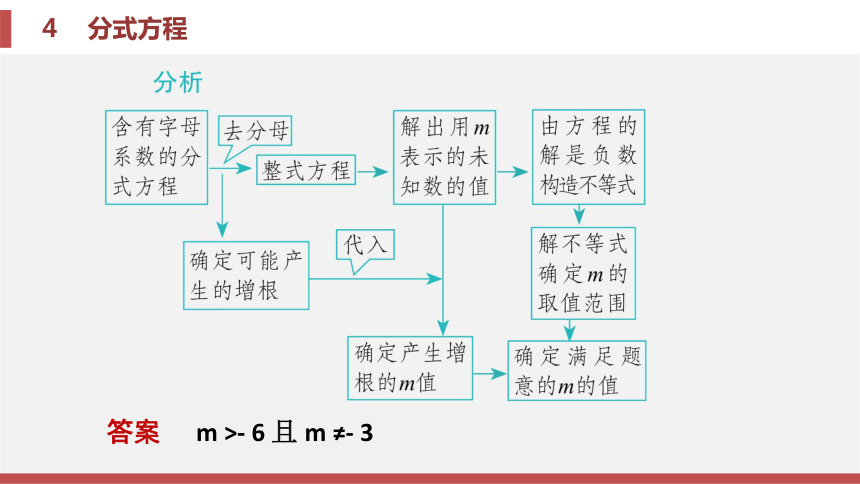
( 1 ) “去” , 即去分母 , 将原分式方程化为整式方程 . ( 2 ) “解” , 即解这个整式方程 . ( 3 ) “验” , 即验根 . 注意:检验是解分式方程的必要步骤 , 当整式方程的根满足最简公分母不为 0 时 , 它是原分式方程的根 , 否则就是原分式方程的增根 , 原分式方程无解. 题型二 根据分式方程解的情况求解相关字母的值 例题2 若关于 x 的方程 的解是 负数 , 则 m 的取值范围为____________. 答案 m >- 6 且 m ≠- 3 例题3 若关于 x 的方程 有解 ,求 m 的取值范围 . 解 方程两边都乘 ( x - 3) , 得 x - 2 = m + 2( x - 3). 解这个方程 , 得 x = 4 - m. 因为原方程有解 , 所以 x = 4 - m 不是原方程的增根 , 即 x = 4 - m 不能使最简公分母为零 , 所以 4 - m ≠ 3 , 即 m ≠ 1 .
综上所述 , 关于 x 的方程 有解时 ,
m 的取值范围是 m ≠ 1 . 锦囊妙计
根据分式方程解的情况求待定字母的值的步骤
( 1 ) 将分式方程化为整式方程 , 求出用待定字母表示的方程的解;
( 2 ) 根据已知条件确定待定字母的取值范围;
( 3 ) 去掉方程有增根时待定字母的取值;
( 4 ) 确定待定字母的取值或取值范围 . 题型三 分式方程的增根、无解问题 例题4 当 m 为何值时 , 方程
会产生增根? 解 方程两边都乘 ( x + 1)( x - 1 ) , 得 2( x - 1 ) - 5( x + 1) = m. 解这个方程 , 得 x =- 当 x =- 1 或 x = 1 时 , 原方程产生增根 .
当 - =- 1 时 , m =- 4 ;
当 - = 1 时 , m =- 10 . 所以当 m 的值为 - 4 或 - 10 时 , 原方程会产生增根 . 例题5 已知关于 x 的方程 = -1无解 , 求 m 的值 . 解 方程两边都乘 ( x - 3) , 得 3 - 2 x - (2 - mx ) =- ( x - 3) . 整理 , 得 ( 1 - m ) x =- 2 . 因为原分式方程无解 ,所以 m = 1 或
x = = 3 ,所以 m = 1 或 m = . 锦囊妙计
由分式方程无解确定字母的值的一般步骤
( 1 ) 去分母 , 得整式方程; ( 2 ) 先确定使整式方程无解时字母的值; ( 3 ) 使最简公分母为零; ( 4 ) 求出使最简公分母为零的未知数的值; ( 5 ) 将未知数的值代入整式方程 , 确定字母的值; ( 6 ) 根据 ( 2 )( 5 ) 确定字母的值 . 题型四 分式方程的实际应用 例题6 在某文具厂要加工一种学生作图工具2500 套 , 在加工了 1000 套后 , 采用了新技术 , 使每天的工作效率提高到原来的 1 . 5 倍 , 结果提前 5 天完成任务 , 那么该文具厂原来每天加工多少套这种学生作图工具?解 设该文具厂原来每天加工 x 套这种学生作图工具 , 根据题意 , 得
解这个方程 , 得 x = 100 . 经检验 , x = 100 是所列方程的解 , 且符合题意 . 所以 , 该文具厂原来每天加工 100 套这种学生作图工具 .例题7 某校准备购买一批笔记本奖励给八年级的优秀学生 , 在购买时发现每本笔记本可以打九折 , 用 360 元钱购买的笔记本 , 打折后购买的数量比打折前多 10 本.
(1) 打折前每本笔记本的售价是多少元?
(2) 由于考虑学生的需求不同 , 学校决定购买笔记本和笔袋共 90 件 , 笔袋每个原售价为 6 元 , 两种物品都打九折 . 若购买总金额不低于 360 元 , 且不超过 365 元 , 有哪几种购买方案?分析 (1) 设打折前每本笔记本的售价为 x 元 ,则打折后每本笔记本的售价为 0 . 9 x 元 , 用含 x 的代数式表示出打折前后可购买的数量 , 再由“打折后购买的数量比打折前多 10 本”得出方程 , 解方程即可;
( 2 ) 设购买笔记本 y 本 , 则购买笔袋 (90 - y ) 个 , 根据购买总金额不低于 360 元 , 且不超过 365 元 , 可得出不等式组 , 求解即可 . 解 (1) 设打折前每本笔记本的售价为 x 元 , 则打折后每本笔记本的售价为 0 . 9 x 元 ,
根据题意 , 得 .解这个方程 , 得 x = 4 .
经检验 , x = 4 是所列方程的根且符合题意 . 所以 , 打折前每本笔记本的售价为 4 元. (2) 设购买笔记本 y 本 , 则购买笔袋 (90 - y ) 个 , 根据题意 , 得 360 ≤ 4 × 0 . 9 × y + 6 × 0 . 9 × (90 - y ) ≤ 365 .
解得 67 ≤ y ≤ 70 . ∵ y 为正整数 , ∴ y 可取 68 , 69 , 70 . 故有三种购买方案: 方案一:购买笔记本 68 本 , 购买笔袋 22 个; 方案二:购买笔记本 69 本 , 购买笔袋 21 个; 方案三:购买笔记本 70 本 , 购买笔袋 20 个 . 锦囊妙计
列分式方程解应用题的策略
列分式方程解应用题的关键是寻找等量关系 , 一般涉及几种未知量就从这几种未知量方面依次寻找等量关系 . 如涉及“单价、数量、总价” , 如果单价、数量未知 , 就从单价、数量方面寻找等量关系 .
设未知数时 , 一般以题目所求的量的等量关系为依据设未知数 , 以其他等量关系为依据列方程 . 如求甲、乙的单价 , 可设甲的单价为未知数 x, 并利用单价方面的等量关系表示出乙的单价 , 再利用数量方面的等量关系列方程 . 当然也应具体问题具体分析 . 将等量关系 ( 文字形式 ) 译为数学符号的过程就是列方程 , 在列分式方程的过程中 , 一般用基本数量关系将各个量联系起来 , 如甲的数量
= . 注意量与 量之间 的对应关系 , 不要混淆 .
谢 谢 观 看!
方程两边都相乘 ( 2 x - 1 ) , 得 2 x - 5 = 3 ( 2 x - 1 ) .
解这个方程,得x=
经检验 , x= 是原方程的根 .方程两边都乘 x ( x + 1 ) , 得 5 x + 2 = 3 x. 解这个方程 , 得 x =- 1 . 检验:当 x =- 1 时 , x ( x + 1 ) =- 1 × ( - 1 + 1 ) = 0 . 所以 x =- 1 是原分式方程的增根 , 所以原方程无解 . 锦囊妙计
解分式方程的三个步骤
( 1 ) “去” , 即去分母 , 将原分式方程化为整式方程 . ( 2 ) “解” , 即解这个整式方程 . ( 3 ) “验” , 即验根 . 注意:检验是解分式方程的必要步骤 , 当整式方程的根满足最简公分母不为 0 时 , 它是原分式方程的根 , 否则就是原分式方程的增根 , 原分式方程无解. 题型二 根据分式方程解的情况求解相关字母的值 例题2 若关于 x 的方程 的解是 负数 , 则 m 的取值范围为____________. 答案 m >- 6 且 m ≠- 3 例题3 若关于 x 的方程 有解 ,求 m 的取值范围 . 解 方程两边都乘 ( x - 3) , 得 x - 2 = m + 2( x - 3). 解这个方程 , 得 x = 4 - m. 因为原方程有解 , 所以 x = 4 - m 不是原方程的增根 , 即 x = 4 - m 不能使最简公分母为零 , 所以 4 - m ≠ 3 , 即 m ≠ 1 .
综上所述 , 关于 x 的方程 有解时 ,
m 的取值范围是 m ≠ 1 . 锦囊妙计
根据分式方程解的情况求待定字母的值的步骤
( 1 ) 将分式方程化为整式方程 , 求出用待定字母表示的方程的解;
( 2 ) 根据已知条件确定待定字母的取值范围;
( 3 ) 去掉方程有增根时待定字母的取值;
( 4 ) 确定待定字母的取值或取值范围 . 题型三 分式方程的增根、无解问题 例题4 当 m 为何值时 , 方程
会产生增根? 解 方程两边都乘 ( x + 1)( x - 1 ) , 得 2( x - 1 ) - 5( x + 1) = m. 解这个方程 , 得 x =- 当 x =- 1 或 x = 1 时 , 原方程产生增根 .
当 - =- 1 时 , m =- 4 ;
当 - = 1 时 , m =- 10 . 所以当 m 的值为 - 4 或 - 10 时 , 原方程会产生增根 . 例题5 已知关于 x 的方程 = -1无解 , 求 m 的值 . 解 方程两边都乘 ( x - 3) , 得 3 - 2 x - (2 - mx ) =- ( x - 3) . 整理 , 得 ( 1 - m ) x =- 2 . 因为原分式方程无解 ,所以 m = 1 或
x = = 3 ,所以 m = 1 或 m = . 锦囊妙计
由分式方程无解确定字母的值的一般步骤
( 1 ) 去分母 , 得整式方程; ( 2 ) 先确定使整式方程无解时字母的值; ( 3 ) 使最简公分母为零; ( 4 ) 求出使最简公分母为零的未知数的值; ( 5 ) 将未知数的值代入整式方程 , 确定字母的值; ( 6 ) 根据 ( 2 )( 5 ) 确定字母的值 . 题型四 分式方程的实际应用 例题6 在某文具厂要加工一种学生作图工具2500 套 , 在加工了 1000 套后 , 采用了新技术 , 使每天的工作效率提高到原来的 1 . 5 倍 , 结果提前 5 天完成任务 , 那么该文具厂原来每天加工多少套这种学生作图工具?解 设该文具厂原来每天加工 x 套这种学生作图工具 , 根据题意 , 得
解这个方程 , 得 x = 100 . 经检验 , x = 100 是所列方程的解 , 且符合题意 . 所以 , 该文具厂原来每天加工 100 套这种学生作图工具 .例题7 某校准备购买一批笔记本奖励给八年级的优秀学生 , 在购买时发现每本笔记本可以打九折 , 用 360 元钱购买的笔记本 , 打折后购买的数量比打折前多 10 本.
(1) 打折前每本笔记本的售价是多少元?
(2) 由于考虑学生的需求不同 , 学校决定购买笔记本和笔袋共 90 件 , 笔袋每个原售价为 6 元 , 两种物品都打九折 . 若购买总金额不低于 360 元 , 且不超过 365 元 , 有哪几种购买方案?分析 (1) 设打折前每本笔记本的售价为 x 元 ,则打折后每本笔记本的售价为 0 . 9 x 元 , 用含 x 的代数式表示出打折前后可购买的数量 , 再由“打折后购买的数量比打折前多 10 本”得出方程 , 解方程即可;
( 2 ) 设购买笔记本 y 本 , 则购买笔袋 (90 - y ) 个 , 根据购买总金额不低于 360 元 , 且不超过 365 元 , 可得出不等式组 , 求解即可 . 解 (1) 设打折前每本笔记本的售价为 x 元 , 则打折后每本笔记本的售价为 0 . 9 x 元 ,
根据题意 , 得 .解这个方程 , 得 x = 4 .
经检验 , x = 4 是所列方程的根且符合题意 . 所以 , 打折前每本笔记本的售价为 4 元. (2) 设购买笔记本 y 本 , 则购买笔袋 (90 - y ) 个 , 根据题意 , 得 360 ≤ 4 × 0 . 9 × y + 6 × 0 . 9 × (90 - y ) ≤ 365 .
解得 67 ≤ y ≤ 70 . ∵ y 为正整数 , ∴ y 可取 68 , 69 , 70 . 故有三种购买方案: 方案一:购买笔记本 68 本 , 购买笔袋 22 个; 方案二:购买笔记本 69 本 , 购买笔袋 21 个; 方案三:购买笔记本 70 本 , 购买笔袋 20 个 . 锦囊妙计
列分式方程解应用题的策略
列分式方程解应用题的关键是寻找等量关系 , 一般涉及几种未知量就从这几种未知量方面依次寻找等量关系 . 如涉及“单价、数量、总价” , 如果单价、数量未知 , 就从单价、数量方面寻找等量关系 .
设未知数时 , 一般以题目所求的量的等量关系为依据设未知数 , 以其他等量关系为依据列方程 . 如求甲、乙的单价 , 可设甲的单价为未知数 x, 并利用单价方面的等量关系表示出乙的单价 , 再利用数量方面的等量关系列方程 . 当然也应具体问题具体分析 . 将等量关系 ( 文字形式 ) 译为数学符号的过程就是列方程 , 在列分式方程的过程中 , 一般用基本数量关系将各个量联系起来 , 如甲的数量
= . 注意量与 量之间 的对应关系 , 不要混淆 .
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
