北师大版 八年级数学下册1.3 线段的垂直平分线课件(共16张)
文档属性
| 名称 | 北师大版 八年级数学下册1.3 线段的垂直平分线课件(共16张) |  | |
| 格式 | zip | ||
| 文件大小 | 500.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 12:55:00 | ||
图片预览





文档简介
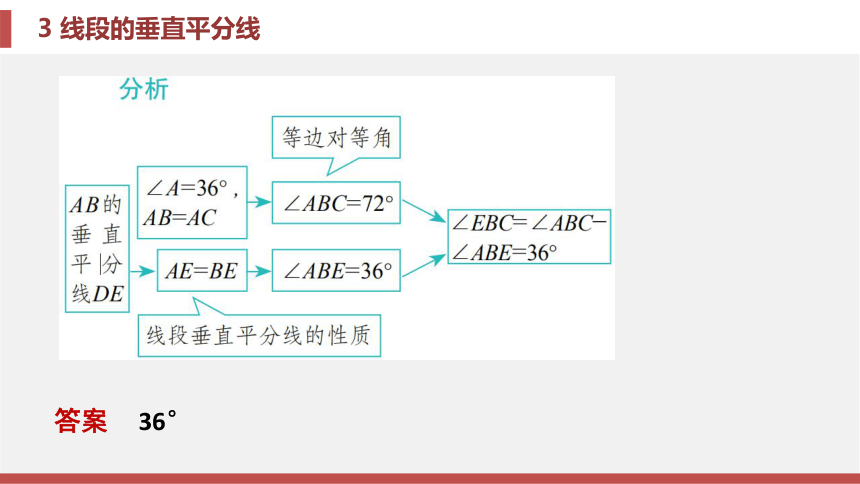
课件16张PPT。第一章 三角形的证明3 线段的垂直平分线第一章 三角形的证明3 线段的垂直平分线考场对接 题型一 利用线段垂直平分线的性质进行相关计算考场对接 例题1 [黄冈中考] 如 图1-3-12, 在△ABC中, AB=AC,
∠A=36°, AB的垂直平分线交AC于点E, 垂足为D, 连
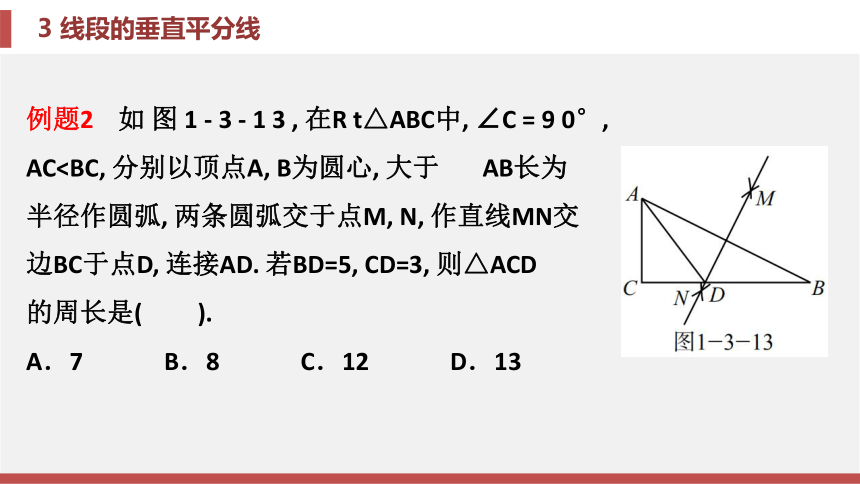
接BE, 则∠EBC的度数为______________.答案 36°例题2 如 图 1 - 3 - 1 3 , 在R t△ABC中, ∠C = 9 0°,
AC半径作圆弧, 两条圆弧交于点M, N, 作直线MN交
边BC于点D, 连接AD. 若BD=5, CD=3, 则△ACD
的周长是( ).
A.7 B.8 C.12 D.13答案 C分析 由尺规作图可知, MN是线段AB的垂直平分线,
∴AD=BD=5.
在Rt△ACD中, AC =4,
则△ACD的周长=AC+CD+AD=12. 故选C.锦囊妙计
由线段垂直平分线得到的结论
已知一条直线是某线段的垂直平分线, 可以得出很多结论, 例如例题1中由直线DE是线段AB的垂直平分线, 易得出下列结论:
(1)∠ADE=∠BDE=90°;
(2)AD=BD;
(3)AE=BE;
(4)∠ABE=∠BAE.题型二 线段垂直平分线的判定例题3 如图1-3-14, AD是△ABC的角平分线, DE, DF分别是△ABD和△ACD的高. 求证:AD垂直平分EF.证明 ∵AD平分∠BAC, DE⊥AB, DF⊥AC,
∴∠EAD=∠FAD, ∠DEA=∠DFA=90°.
又∵AD=AD, ∴△ADE≌△ADF,
∴DE=DF, AE=AF,
∴点A, D在线段EF的垂直平分线上,
∴AD垂直平分EF.锦囊妙计
线段垂直平分线的判定方法
(1)根据线段垂直平分线的定义来判定;
(2)证明直线上有两个点到线段两个端点的距离分别相等, 根据两点确定一条直线, 可以判定这两点所在的直线就是这条线段的垂直平分线.题型三 线段垂直平分线的实际应用例题4 [重庆中考]为进一步打造“宜居重庆”,
某区拟在新竣工的长方形广场的内部修建一
个音乐喷泉, 要求音乐喷泉M到广场的两个入
口A, B的距离相等, 且到广场管理处C的距离
等于A和B之间距离的一半, A, B, C的位置如
图1-3-15所示.请利用尺规作图作出音乐喷泉M的位置.(要求:
不写已知、求作和作法, 保留作图痕迹, 写出结论)解 如图1-3-15, 作线段AB的垂直平分线, 以点C为圆心, AB的长为半径画弧交AB的垂直平分线于点M, 则点M就是音乐喷泉的位置.锦囊妙计
作图选点性问题
若要找到某两个点的距离相等的点, 一般先画出这两点所连线段的垂直平分线, 然后在该垂直平分线上去找.
谢 谢 观 看!
∠A=36°, AB的垂直平分线交AC于点E, 垂足为D, 连
接BE, 则∠EBC的度数为______________.答案 36°例题2 如 图 1 - 3 - 1 3 , 在R t△ABC中, ∠C = 9 0°,
AC
边BC于点D, 连接AD. 若BD=5, CD=3, 则△ACD
的周长是( ).
A.7 B.8 C.12 D.13答案 C分析 由尺规作图可知, MN是线段AB的垂直平分线,
∴AD=BD=5.
在Rt△ACD中, AC =4,
则△ACD的周长=AC+CD+AD=12. 故选C.锦囊妙计
由线段垂直平分线得到的结论
已知一条直线是某线段的垂直平分线, 可以得出很多结论, 例如例题1中由直线DE是线段AB的垂直平分线, 易得出下列结论:
(1)∠ADE=∠BDE=90°;
(2)AD=BD;
(3)AE=BE;
(4)∠ABE=∠BAE.题型二 线段垂直平分线的判定例题3 如图1-3-14, AD是△ABC的角平分线, DE, DF分别是△ABD和△ACD的高. 求证:AD垂直平分EF.证明 ∵AD平分∠BAC, DE⊥AB, DF⊥AC,
∴∠EAD=∠FAD, ∠DEA=∠DFA=90°.
又∵AD=AD, ∴△ADE≌△ADF,
∴DE=DF, AE=AF,
∴点A, D在线段EF的垂直平分线上,
∴AD垂直平分EF.锦囊妙计
线段垂直平分线的判定方法
(1)根据线段垂直平分线的定义来判定;
(2)证明直线上有两个点到线段两个端点的距离分别相等, 根据两点确定一条直线, 可以判定这两点所在的直线就是这条线段的垂直平分线.题型三 线段垂直平分线的实际应用例题4 [重庆中考]为进一步打造“宜居重庆”,
某区拟在新竣工的长方形广场的内部修建一
个音乐喷泉, 要求音乐喷泉M到广场的两个入
口A, B的距离相等, 且到广场管理处C的距离
等于A和B之间距离的一半, A, B, C的位置如
图1-3-15所示.请利用尺规作图作出音乐喷泉M的位置.(要求:
不写已知、求作和作法, 保留作图痕迹, 写出结论)解 如图1-3-15, 作线段AB的垂直平分线, 以点C为圆心, AB的长为半径画弧交AB的垂直平分线于点M, 则点M就是音乐喷泉的位置.锦囊妙计
作图选点性问题
若要找到某两个点的距离相等的点, 一般先画出这两点所连线段的垂直平分线, 然后在该垂直平分线上去找.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
