北师大版 八年级数学下册1.4 角平分线课件(共33张)
文档属性
| 名称 | 北师大版 八年级数学下册1.4 角平分线课件(共33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 962.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览








文档简介
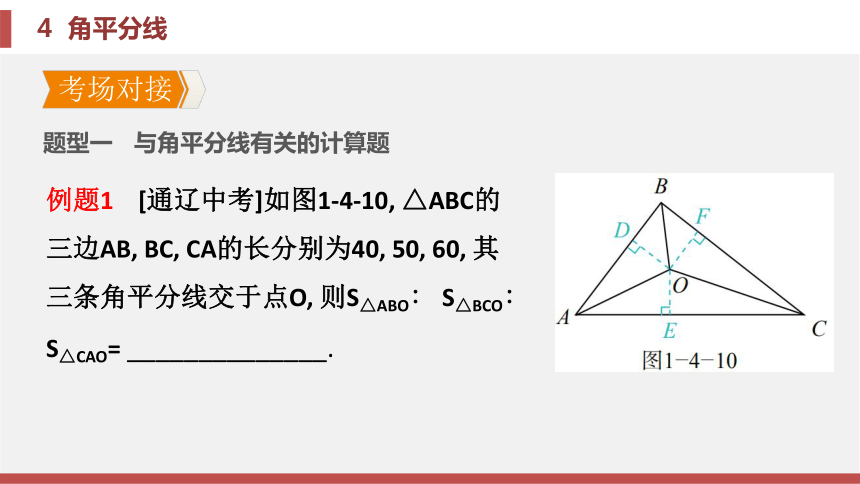
课件33张PPT。第一章 三角形的证明4 角平分线第一章 三角形的证明4 角平分线考场对接 题型一 与角平分线有关的计算题分析 根据角平分线的性质, 可知点O到△ABC三边的距离相等.过点O作三边的垂线段(如图1-4-10), 可得OD=OF=OE, 因此△ABO, △BCO,
△CAO的面积之比等于AB, BC, CA的长度之比.答案 4∶5∶6锦囊妙计
利用三角形角平分线的性质巧解面积问题
(1)利用三角形角平分线的交点到各边的距离相等添加垂线段;
(2)通过角平分线的交点与三角形各顶点的连线构建三个三角形;
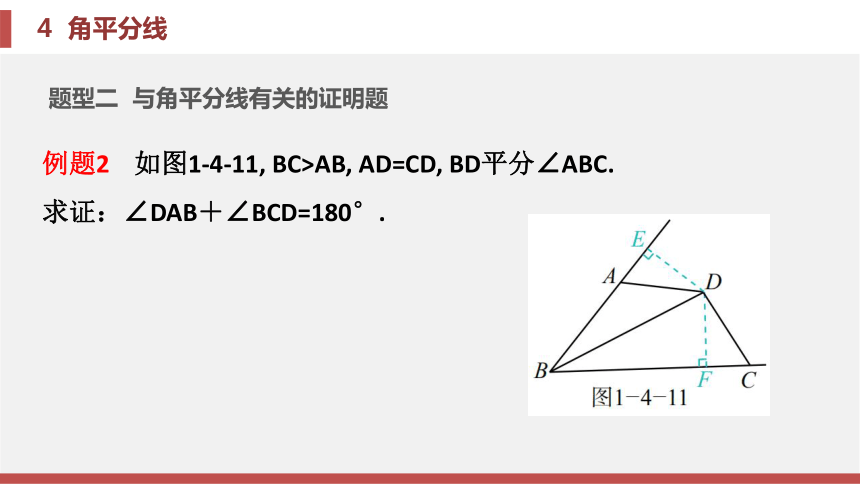
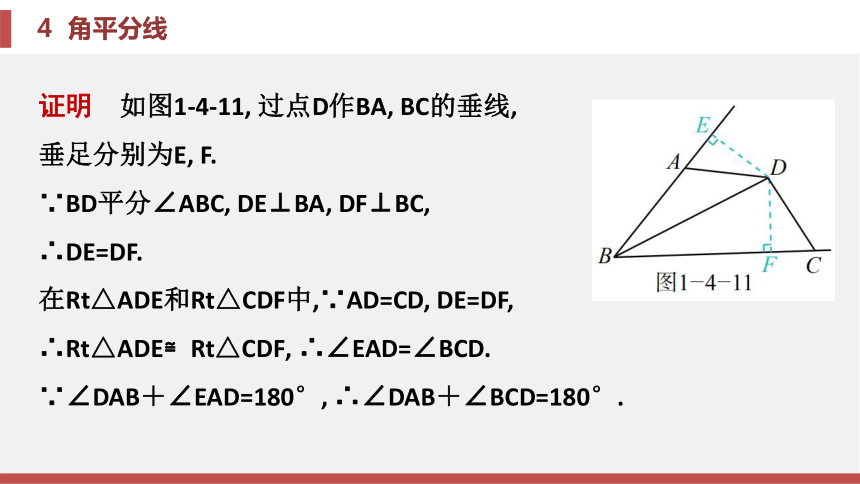
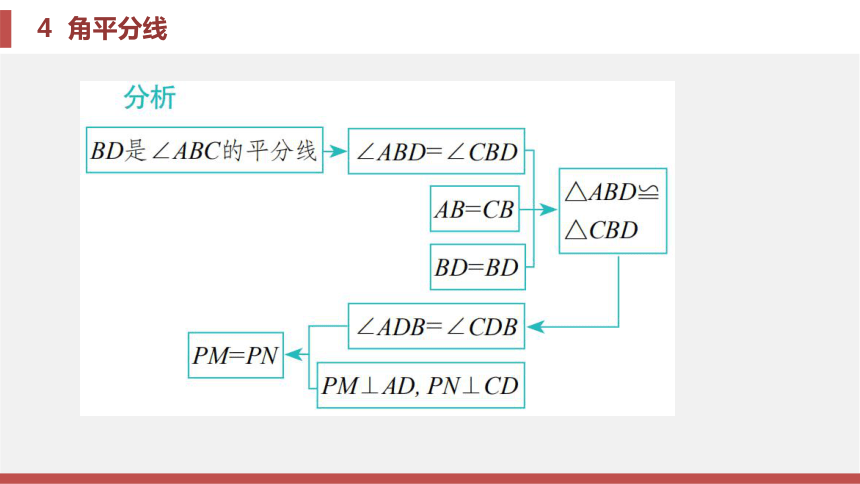
(3)根据“在等高的情况下, 面积之比等于对应底之比”求解.题型二 与角平分线有关的证明题证明 ∵BD为∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
∵AB=CB, ∠ABD=∠CBD, BD=BD,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
∵点P在BD上, PM⊥AD, PN⊥CD,
∴PM=PN.锦囊妙计
巧添辅助线妙解有关角平分线的问题
当运用已知条件无法解决问题时, 应考虑添加适当的辅助线来创造条件. 遇到角平分线, 应想到“向角的两边作垂线段”这种常见的辅助线作法.题型三 角平分线的实际应用分析 在阴影区域内, 到公路和铁路的距离相等的点在这两条路所夹
锐角的平分线上, 即作公路与铁路所夹锐角的平分线OC, 并按照比例尺在射线OC上截取OD=1.6 cm.锦囊妙计
尺规作角平分线的应用
几何问题中, 涉及探索“到角两边距离相等”的某点的位置, 可通过尺规作角平分线来解决. 解题时, 需要注意与线段垂直平分线的作法和应用的区别.题型四 角平分线与平行线的综合应用证明 ∵BE=EO, ∴∠EBO=∠EOB.
∵在△ABC中, ∠ABC与∠ACB的平分线交于点O,
∴∠EBO=∠OBC, ∠OCB=∠OCF, ∴∠EOB=∠OBC,
∴EF∥BC, 从而∠FOC=∠OCB=∠OCF,
∴OF=CF.锦囊妙计
构造等腰三角形的“四个方法”
(1)“角平分线+平行线”构造等腰三角形,应用平行线的性质得到角的相等关系,应用等角对等边得到边的相等关系.
(2)“角平分线+垂线”构造等腰三角形,逆用等腰三角形“三线合一”的性质定理.
(3)应用“垂直平分线”构造等腰三角形.
(4)用“三角形中角的2倍关系+角平分线”构造等腰三角形.题型五 角平分线与线段垂直平分线的综合应用(2)∵AD平分∠BAC, ∴∠EAD=∠FAD.
在△AED和△AFD中,
∵∠AED=∠AFD=90°, ∠EAD=∠FAD, AD=AD,
∴△AED≌△AFD(AAS), ∴AE=AF.
设BE=x, 则CF=x.
∵AB=5, AC=3, AE=AB-BE, AF=AC+CF,
∴5-x=3+x,
解得x=1, ∴BE=1, AE=AB-BE=5-1=4.锦囊妙计
证明线段相等的常用方法
(1)利用全等三角形证明;
(2)利用等腰三角形的性质证明;
(3)利用线段垂直平分线的性质证明;
(4)利用角平分线的性质证明.题型六 角平分线性质和判定的综合应用锦囊妙计
巧添辅助线妙解角平分线问题
添加辅助线, 构造角平分线性质、判定的基本图形, 可巧妙解决相关问题.
谢 谢 观 看!
△CAO的面积之比等于AB, BC, CA的长度之比.答案 4∶5∶6锦囊妙计
利用三角形角平分线的性质巧解面积问题
(1)利用三角形角平分线的交点到各边的距离相等添加垂线段;
(2)通过角平分线的交点与三角形各顶点的连线构建三个三角形;
(3)根据“在等高的情况下, 面积之比等于对应底之比”求解.题型二 与角平分线有关的证明题证明 ∵BD为∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
∵AB=CB, ∠ABD=∠CBD, BD=BD,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
∵点P在BD上, PM⊥AD, PN⊥CD,
∴PM=PN.锦囊妙计
巧添辅助线妙解有关角平分线的问题
当运用已知条件无法解决问题时, 应考虑添加适当的辅助线来创造条件. 遇到角平分线, 应想到“向角的两边作垂线段”这种常见的辅助线作法.题型三 角平分线的实际应用分析 在阴影区域内, 到公路和铁路的距离相等的点在这两条路所夹
锐角的平分线上, 即作公路与铁路所夹锐角的平分线OC, 并按照比例尺在射线OC上截取OD=1.6 cm.锦囊妙计
尺规作角平分线的应用
几何问题中, 涉及探索“到角两边距离相等”的某点的位置, 可通过尺规作角平分线来解决. 解题时, 需要注意与线段垂直平分线的作法和应用的区别.题型四 角平分线与平行线的综合应用证明 ∵BE=EO, ∴∠EBO=∠EOB.
∵在△ABC中, ∠ABC与∠ACB的平分线交于点O,
∴∠EBO=∠OBC, ∠OCB=∠OCF, ∴∠EOB=∠OBC,
∴EF∥BC, 从而∠FOC=∠OCB=∠OCF,
∴OF=CF.锦囊妙计
构造等腰三角形的“四个方法”
(1)“角平分线+平行线”构造等腰三角形,应用平行线的性质得到角的相等关系,应用等角对等边得到边的相等关系.
(2)“角平分线+垂线”构造等腰三角形,逆用等腰三角形“三线合一”的性质定理.
(3)应用“垂直平分线”构造等腰三角形.
(4)用“三角形中角的2倍关系+角平分线”构造等腰三角形.题型五 角平分线与线段垂直平分线的综合应用(2)∵AD平分∠BAC, ∴∠EAD=∠FAD.
在△AED和△AFD中,
∵∠AED=∠AFD=90°, ∠EAD=∠FAD, AD=AD,
∴△AED≌△AFD(AAS), ∴AE=AF.
设BE=x, 则CF=x.
∵AB=5, AC=3, AE=AB-BE, AF=AC+CF,
∴5-x=3+x,
解得x=1, ∴BE=1, AE=AB-BE=5-1=4.锦囊妙计
证明线段相等的常用方法
(1)利用全等三角形证明;
(2)利用等腰三角形的性质证明;
(3)利用线段垂直平分线的性质证明;
(4)利用角平分线的性质证明.题型六 角平分线性质和判定的综合应用锦囊妙计
巧添辅助线妙解角平分线问题
添加辅助线, 构造角平分线性质、判定的基本图形, 可巧妙解决相关问题.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
