北师大版 八年级数学下册1.1 等腰三角形课件(共42张)
文档属性
| 名称 | 北师大版 八年级数学下册1.1 等腰三角形课件(共42张) |  | |
| 格式 | zip | ||
| 文件大小 | 984.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 13:02:36 | ||
图片预览











文档简介
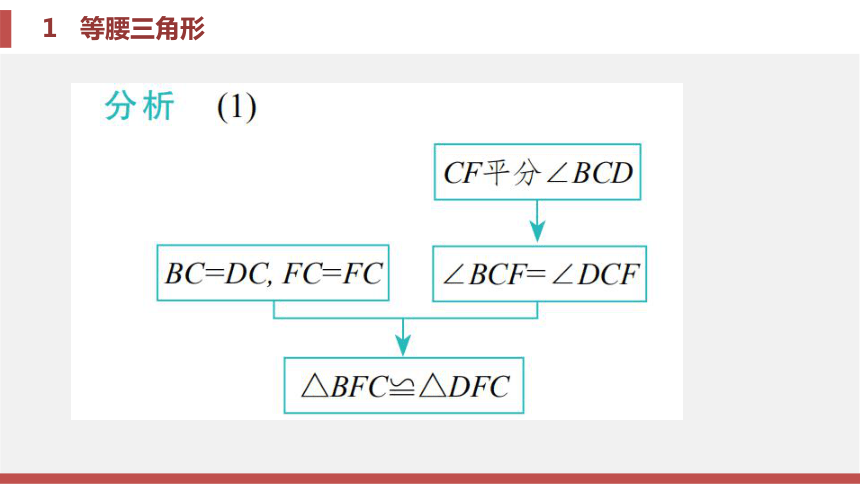
课件42张PPT。第一章 三角形的证明1 等腰三角形第一章 三角形的证明1 等腰三角形考场对接 题型一 运用全等三角形的性质与判定进行证明证明 (1)∵CF平分∠BCD,
∴∠BCF=∠DCF.
在△BFC和△DFC中, ∵BC=DC, ∠BCF=∠DCF, FC=FC,
∴△BFC≌△DFC.锦囊妙计
证明两边相等的方法
一是证明两边所在的两个三角形全等;
二是证明一个三角形中的两角相等.题型二 运用等腰三角形的性质证明线段相等锦囊妙计
证明线段相等的方法
(1)证明其所在的两个三角形全等;
(2)若要证明的两条线段在同一个三角形中, 则可证明所在三角形中所对的两个角相等;
(3)借助等腰三角形三线合一的性质. 有关等腰三角形问题常用的添加辅助线的方法:作底边上的高或底边上的中线或顶角的平分线.题型三 运用等腰三角形的性质进行角度计算解 ∵HE=HF, ∠E=25°,
∴∠EFH=∠E=25°,
∴∠FHG=∠E+∠EFH=50°.
∵AB∥CD,
∴∠HFG=∠FGC=62°,
∴∠FGH=180°-∠FHG-∠HFG
=180°-50°-62°
=68°.锦囊妙计
运用等腰三角形的性质求角度的关键
运用等腰三角形的性质进行角度计算时, 常应用三角形的内角和定理和外角、内角的关系, 通过等腰三角形的两底角相等联系在一起, 再列方程求解.题型四 与等边三角形有关的计算、证明解 (1)△DEF是等边三角形. 证明如下:
∵△ABC是等边三角形,
∴∠A=∠B=∠C, AB=BC=AC.
又∵AD=BE=CF, ∴DB=EC=FA,
∴△ADF≌△BED≌△CFE,
∴DF=ED=FE, ∴△DEF是等边三角形.锦囊妙计
等边三角形的判定方法
(1)定义法;
(2)先证三角形是等腰三角形, 再证有一个角为60°;
(3)证三个角相等.题型五 含30°角的直角三角形性质的应用锦囊妙计
利用含30°角的直角三角形的性质解题
利用“在直角三角形中, 如果一个锐角等于30°, 那么它所对的直角边等于斜边的一半”解题的关键是设法寻找含有30°角的直角三角形. 方法一般有两种:一是通过作垂线段构造;二是证明角的度数是90°.题型六 反证法的运用例题6 求证:在一个三角形中, 至少有两个内角是锐角.证明 (1)假设△ABC中只有一个内角是锐角,
不妨设∠A<90°, ∠B≥90°, ∠C≥90°,
于是, ∠A+∠B+∠C>180°, 这与三角形内角
和定理相矛盾;
(2)假设△ABC中没有内角是锐角, 即∠A≥90°, ∠B≥90°,∠C≥90°,
于是, ∠A+∠B+∠C>180°, 这与三角形内角和
定理相矛盾.
所以假设不成立, 则原结论是正确的.锦囊妙计
用反证法证明命题的策略
(1)用反证法证明命题时, 原结论的反面一定要找准确、全面;
(2)用反证法证明命题时, 一定要注意步骤:先进行合理的假设, 再推出矛盾, 最后得出结论;
(3)用反证法证明与平面几何有关的命题时, 一般先根据命题写出已知、求证, 并画出相应的图形, 再证明.题型七 与等腰三角形有关的分类讨论题例题7 如果一个等腰三角形的一边长为4 cm, 另一边长为5 cm, 那么它的周长为( ).
A.14 cm B.13 cm
C.14 cm或13 cm D.无法计算分析 分为两种情况:①底边长为4 cm, 腰长为5 cm;②底边长为
5 cm, 腰长为4 cm. 具体的解答过程如下:
∵等腰三角形的两边长分别是4 cm和5 cm, ∴应分为两种情况:
①当底边长为4 cm, 腰长为5 cm时,三角形的周长4+5+5=14(cm);
②当底边长为5 cm,腰长为4 cm时, 三角形的周长5+4+4=13(cm),
∴它的周长是14 cm或13 cm.
故选C.答案 C例题8 已知等腰三角形的一个内角为40°, 则这个等腰三角形顶角的度数为( ).
A.40° B.100°
C.40°或100° D.50°或70°答案 C锦囊妙计
等腰三角形中常见的分类讨论问题
(1)当腰和底边不能确定时, 必须进行分类讨论.
(2)当顶角和底角不能确定时, 必须进行分类讨论.
(3)当高的位置不能确定时, 必须进行分类讨论.
(4)由腰上的中线引起的分类讨论.题型八 等腰三角形中的动点问题(2)当DC等于多少时, △ABD≌△DCE?请说明△ABD≌△DCE的理由;
(3)在点D的运动过程中, △ADE的形状也在改变. 当∠BDA等于多少度时, △ADE是等腰三角形?解 (1)25 小
(2)当△ABD≌△DCE时, DC=AB.
∵AB=2, ∴DC=2, ∴当DC等于2时, △ABD≌△DCE.
理由如下:
∵∠ABD=40°, ∠ADE=40°,
∴∠BAD+∠BDA=140°, ∠CDE+∠BDA=140°,∴∠BAD=∠CDE.
∵AB=AC, ∴∠B=∠C.
在△ABD和△DCE中, ∵∠B=∠C, AB=DC, ∠BAD=∠CDE,
∴△ABD≌△DCE.锦囊妙计
解决等腰三角形动点问题的策略
第一步:化动为静, 以静制动, 确定特殊位置, 并画出满足条件的图形.
第二步:依据题中数量关系、等腰三角形的性质或判定定理, 构建相关点、线之间的特殊图形.
第三步:求解问题.
谢 谢 观 看!
∴∠BCF=∠DCF.
在△BFC和△DFC中, ∵BC=DC, ∠BCF=∠DCF, FC=FC,
∴△BFC≌△DFC.锦囊妙计
证明两边相等的方法
一是证明两边所在的两个三角形全等;
二是证明一个三角形中的两角相等.题型二 运用等腰三角形的性质证明线段相等锦囊妙计
证明线段相等的方法
(1)证明其所在的两个三角形全等;
(2)若要证明的两条线段在同一个三角形中, 则可证明所在三角形中所对的两个角相等;
(3)借助等腰三角形三线合一的性质. 有关等腰三角形问题常用的添加辅助线的方法:作底边上的高或底边上的中线或顶角的平分线.题型三 运用等腰三角形的性质进行角度计算解 ∵HE=HF, ∠E=25°,
∴∠EFH=∠E=25°,
∴∠FHG=∠E+∠EFH=50°.
∵AB∥CD,
∴∠HFG=∠FGC=62°,
∴∠FGH=180°-∠FHG-∠HFG
=180°-50°-62°
=68°.锦囊妙计
运用等腰三角形的性质求角度的关键
运用等腰三角形的性质进行角度计算时, 常应用三角形的内角和定理和外角、内角的关系, 通过等腰三角形的两底角相等联系在一起, 再列方程求解.题型四 与等边三角形有关的计算、证明解 (1)△DEF是等边三角形. 证明如下:
∵△ABC是等边三角形,
∴∠A=∠B=∠C, AB=BC=AC.
又∵AD=BE=CF, ∴DB=EC=FA,
∴△ADF≌△BED≌△CFE,
∴DF=ED=FE, ∴△DEF是等边三角形.锦囊妙计
等边三角形的判定方法
(1)定义法;
(2)先证三角形是等腰三角形, 再证有一个角为60°;
(3)证三个角相等.题型五 含30°角的直角三角形性质的应用锦囊妙计
利用含30°角的直角三角形的性质解题
利用“在直角三角形中, 如果一个锐角等于30°, 那么它所对的直角边等于斜边的一半”解题的关键是设法寻找含有30°角的直角三角形. 方法一般有两种:一是通过作垂线段构造;二是证明角的度数是90°.题型六 反证法的运用例题6 求证:在一个三角形中, 至少有两个内角是锐角.证明 (1)假设△ABC中只有一个内角是锐角,
不妨设∠A<90°, ∠B≥90°, ∠C≥90°,
于是, ∠A+∠B+∠C>180°, 这与三角形内角
和定理相矛盾;
(2)假设△ABC中没有内角是锐角, 即∠A≥90°, ∠B≥90°,∠C≥90°,
于是, ∠A+∠B+∠C>180°, 这与三角形内角和
定理相矛盾.
所以假设不成立, 则原结论是正确的.锦囊妙计
用反证法证明命题的策略
(1)用反证法证明命题时, 原结论的反面一定要找准确、全面;
(2)用反证法证明命题时, 一定要注意步骤:先进行合理的假设, 再推出矛盾, 最后得出结论;
(3)用反证法证明与平面几何有关的命题时, 一般先根据命题写出已知、求证, 并画出相应的图形, 再证明.题型七 与等腰三角形有关的分类讨论题例题7 如果一个等腰三角形的一边长为4 cm, 另一边长为5 cm, 那么它的周长为( ).
A.14 cm B.13 cm
C.14 cm或13 cm D.无法计算分析 分为两种情况:①底边长为4 cm, 腰长为5 cm;②底边长为
5 cm, 腰长为4 cm. 具体的解答过程如下:
∵等腰三角形的两边长分别是4 cm和5 cm, ∴应分为两种情况:
①当底边长为4 cm, 腰长为5 cm时,三角形的周长4+5+5=14(cm);
②当底边长为5 cm,腰长为4 cm时, 三角形的周长5+4+4=13(cm),
∴它的周长是14 cm或13 cm.
故选C.答案 C例题8 已知等腰三角形的一个内角为40°, 则这个等腰三角形顶角的度数为( ).
A.40° B.100°
C.40°或100° D.50°或70°答案 C锦囊妙计
等腰三角形中常见的分类讨论问题
(1)当腰和底边不能确定时, 必须进行分类讨论.
(2)当顶角和底角不能确定时, 必须进行分类讨论.
(3)当高的位置不能确定时, 必须进行分类讨论.
(4)由腰上的中线引起的分类讨论.题型八 等腰三角形中的动点问题(2)当DC等于多少时, △ABD≌△DCE?请说明△ABD≌△DCE的理由;
(3)在点D的运动过程中, △ADE的形状也在改变. 当∠BDA等于多少度时, △ADE是等腰三角形?解 (1)25 小
(2)当△ABD≌△DCE时, DC=AB.
∵AB=2, ∴DC=2, ∴当DC等于2时, △ABD≌△DCE.
理由如下:
∵∠ABD=40°, ∠ADE=40°,
∴∠BAD+∠BDA=140°, ∠CDE+∠BDA=140°,∴∠BAD=∠CDE.
∵AB=AC, ∴∠B=∠C.
在△ABD和△DCE中, ∵∠B=∠C, AB=DC, ∠BAD=∠CDE,
∴△ABD≌△DCE.锦囊妙计
解决等腰三角形动点问题的策略
第一步:化动为静, 以静制动, 确定特殊位置, 并画出满足条件的图形.
第二步:依据题中数量关系、等腰三角形的性质或判定定理, 构建相关点、线之间的特殊图形.
第三步:求解问题.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
