北师大版八年级数学下册 第四章 因式分解章末复习课件(共42张)
文档属性
| 名称 | 北师大版八年级数学下册 第四章 因式分解章末复习课件(共42张) |  | |
| 格式 | zip | ||
| 文件大小 | 683.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 13:08:34 | ||
图片预览










文档简介
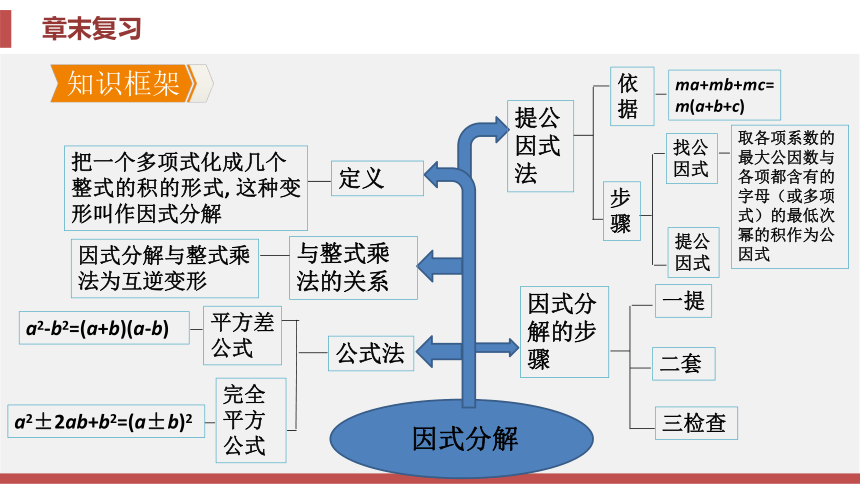
课件42张PPT。第四章 因式分解章末复习第四章 因式分解章末复习【要点指导】常用的因式分解的方法有两种:一是提公因式法, 二是
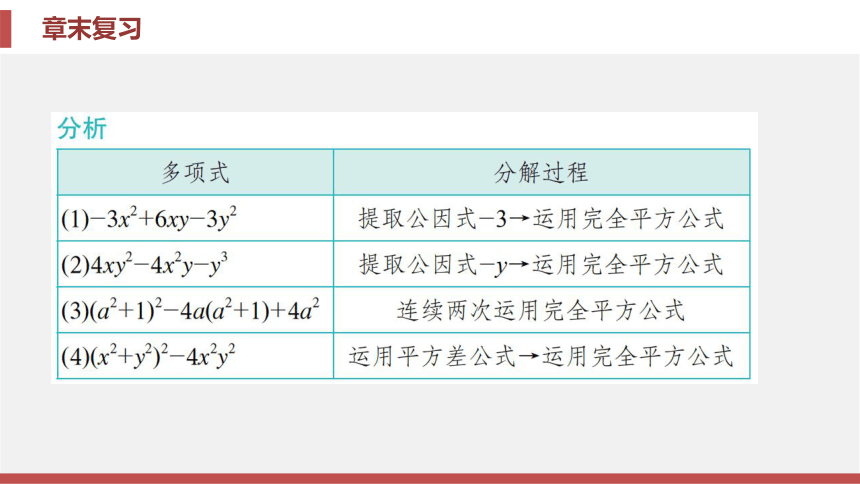
公式法. 其中提公因式法是最基本的方法, 因此在因式分解时, 若多项式有公因式, 则应先提取公因式, 再考虑用其他方法分解. 若多项式是二项式, 则考虑利用提公因式法或运用平方差公式来分解;若多项式是三项式, 则考虑利用提公因式法或运用完全平方公式来分解. 最后检查分解是否彻底.专题一 因式分解的运用技巧例1 将下列各式分解因式:
(1)-3x2+6xy-3y2;
(2)4xy2-4x2y-y3;
(3)(a2+1)2-4a(a2+1)+4a2;
(4)(x2+y2)2-4x2y2. 解 (1)-3x2+6xy-3y2=-3(x2-2xy+y2)=-3(x-y)2.
(2)4xy2-4x2y-y3=-y(4x2-4xy+y2)=-y(2x-y)2.
(3)(a2+1)2-4a(a2+1)+4a2=(a2+1-2a)2 =(a2-2a+1)2=[(a-1)2]2=(a-1)4.
(4)(x2+y2)2-4x2y2=(x2+y2+2xy)(x2+y2-2xy)=(x+y)2(x-y)2.相关题1 把下列各式分解因式:
(1)5x2-15xy+10xy2;
(2)a(x-2)+(2-x)2;
(3)2x2y-8xy+8y;
(4)(m2+n2)2-4m2n2.【要点指导】应用公式a2-b2=(a+b)(a-b), a2±2ab+b2=(a±b)2先将所求的代数式进行变形, 再把相应的值代入计算. 专题二 因式分解与代数式的值例2 若|a+b-6|+(ab-4)2=0, 求-a3b-2a2b2-ab3的值.分析 根据非负数的性质得到a+b=6, ab=4, 将所求代数式进行因式分解, 然后整体代入求值. 解 ∵|a+b-6|+(ab-4)2=0,
∴a+b-6=0且ab-4=0, 则a+b=6, ab=4,
∴-a3b-2a2b2-ab3=-ab(a2+2ab+b2)=-ab(a+b)2=-4×62=-144. A相关题2-1 若x2-3x+2=0, 则x3-x2-4x+10的值是( ).
A.6 B.8 C.10 D.12解析 ∵x2-3x+2=0,∴x3-x2-4x+10=x3-3x2+2x+2x2-6x+4+6=
x(x2-3x+2)+2(x2-3x+2)+6=6.故选A相关题2-2 已知相邻边长分别为a, b的长方形, 它的周长为12, 面积为2, 则代数式a3b+2a2b2+ab3的值为________.72【要点指导】 将一个式子或一个式子的某一部分通过恒等变形为
完全平方式或几个完全平方式的和的形式, 这种方法称为配方法. 配方法常被用到式子的恒等变形中, 以挖掘题目中的隐含条件, 是解题的有力手段之一.专题三 配方法例3 已知4x2-20x+8y+y2+41=0, 求-xy的值.分析 观察所给等式左边的特点, 若将41拆成25与16两项, 则可以分组结合配方, 从而利用完全平方式的非负性解决问题.相关题3 求证:不论x取何实数, 多项式-2x4-12x3-18x2的值都不会是正数.【要点指导】 因式分解不仅在数值计算、代数式的化简求值等方面有广泛的应用, 在解决实际问题时也同样重要.通过学习和应用
因式分解, 能使我们的观察能力、运算能力、逻辑思维能力、探究
能力得到提高.专题四 因式分解的应用分析 由于题目中的数字较大, 考虑将分母中的20 212 0192+
20 212 0212-2写成20 212 0192-1+20 212 0212-1, 这样可以直接运用平方差公式进行因式分解, 再提取公因式后进行适当的数字变形即可求解. 相关题4 数学课上老师出了一道题:计算2962的值, 喜欢数学的小亮举手做出这道题, 他的解题过程如下:2962=(300-4)2=3002-2×
300×(-4)+42=90 000+2400+16=92 416.
老师表扬小亮积极发言的同时, 也指出了解题中的错误, 你认为小亮的解题过程错在哪儿, 并写出正确的解答过程.分析 先利用因式分解的方法求出广场铺草坪的面积为a2-4b2=
(a+2b)(a-2b), 再把a, b的值分别代入求出面积, 最后计算要投资的钱数. 例5 在一个边长为a=84 m的正方形广场的四角均留出一个边长为
b=8 m的正方形修建花坛, 其余地方铺草坪, 草坪的面积有多大?如果铺草坪每平方米需5元, 那么给这个广场铺草坪至少要投资多少元?解 广场铺草坪的面积为a2-4b2=(a+2b)(a-2b).
当a=84 m, b=8 m时, a2-4b2=(84+2×8)×(84-2×8)=100×68=6800(m2).
需投资的金额为5×6800=34 000(元).
故草坪的面积为6800 m2, 给这个广场铺草坪至少要投资34 000元.答案 3600 cm2【要点指导】用整体思想解数学题, 就是把一些看似彼此独立而实质是紧密关联的量看成一个整体去设元、列式、变形、消元、代入或求值等. 这样不仅可以摆脱固定模式的束缚, 使复杂的问题变得简单, 让陌生的问题变得熟悉, 往往还可以解决一些用常规方法解决不了的问题.专题 整体思想在因式分解中的应用例 因式分解:(xy-1)2+(x+y-2)(x+y-2xy).解 设x+y=a, xy=b,
则原式=(b-1)2+(a-2)(a-2b)=b2-2b+1+a2-2a+4b-2ab=(a2-2ab+b2)-
(2a-2b)+1=(a-b)2-2(a-b)+1=(a-b-1)2=(x+y-xy-1)2=(x-1)2(y-1)2.相关题 因式分解:
(1)(x+2y)2-2(x+2y)+1;
(2)(a+b)2-4(a+b-1);
(3)(x-1)(x-2)(x-3)(x-4)-120. 母题1 (教材P93随堂练习第2题)
下列由左边到右边的变形, 哪些是因式分解?为什么?
(1)(a+3)(a-3)=a2-9;
(2)m2-4=(m+2)(m-2);
(3)a2-b2+1=(a+b)(a-b)+1;
(4)2mR+2mr=2m(R+r).考点:因式分解的概念.
考情:因式分解的概念在中考中不常出现, 一般只以选择题、填空题的形式出现, 多以单独知识点的形式考查.
策略:因式分解是把一个多项式化为几个整式的积的形式.链接1 [滨州中考]下列各式从左到右的变形中, 属于因式分解的
是( ).
A.a(m+n)=am+an
B.a2-b2-c2=(a-b)(a+b)-c2
C.10x2-5x=5x(2x-1)
D.x2-16+6x=(x+4)(x-4)+6x分析 因式分解是把一个多项式化为几个整式的积的形式, 只有C选项满足, 故选C.答案 C母题2 (教材P104复习题第1题)
把下列各式因式分解:
(1)7x2-63; (2)a3-a; (3)3a2-3b2; (4)y2-9(x+y)2;
(5)a(x-y)-b(y-x)+c(x-y);
(6)x(m+n)-y(n+m)+(m+n);
(7)(x+y)2-16(x-y)2; (8)a2(a-b)2-b2(a-b)2;
(9)(x+y+z)2-(x-y-z)2; (10)(x+y)2-14(x+y)+49. 考点:因式分解.
考情:因式分解是中考的常考考点, 常以选择题、填空题的形式出现, 也会和其他知识点一起考查, 难度较小.
策略:若一个多项式有公因式, 则因式分解时应先提取公因式, 再用公式法进行因式分解, 注意因式分解要彻底, 分解到不能再分解为止.链接2 [泸州中考]分解 因 式 : 2 m 2- 8 =_______________.分析 先提取公因式, 再运用平方差公式分解.2m2-8=2(m2-4)=2(m+2)(m-2). 2(m+2)(m-2)链接3 [安徽中考]因式分解:a2b-4ab+4b= ___________ . 分析 a2b-4ab+4b=b(a2-4a+4)=b(a-2)2. b(a-2)2考点:利用因式分解求代数式的值.
考情:利用因式分解求代数式的值是中考的常考点, 题型比较灵活, 选择题、填空题、解答题都有出现.
策略:通过提公因式法、公式法把多项式变成含有已知条件的形式, 然后直接代入求值即可.链接5 [菏泽中考]已知4x=3y, 求代数式(x-2y)2-(x-y)(x+y)-2y2
的值.解 (x-2y)2-(x-y)(x+y)-2y2=(x2-4xy+4y2)-(x2-y2)-2y2
=x2-4xy+4y2-x2+y2-2y2=-4xy+3y2=-y(4x-3y).
因为4x=3y, 所以4x-3y=0,
所以原式=0.
谢 谢 观 看!
公式法. 其中提公因式法是最基本的方法, 因此在因式分解时, 若多项式有公因式, 则应先提取公因式, 再考虑用其他方法分解. 若多项式是二项式, 则考虑利用提公因式法或运用平方差公式来分解;若多项式是三项式, 则考虑利用提公因式法或运用完全平方公式来分解. 最后检查分解是否彻底.专题一 因式分解的运用技巧例1 将下列各式分解因式:
(1)-3x2+6xy-3y2;
(2)4xy2-4x2y-y3;
(3)(a2+1)2-4a(a2+1)+4a2;
(4)(x2+y2)2-4x2y2. 解 (1)-3x2+6xy-3y2=-3(x2-2xy+y2)=-3(x-y)2.
(2)4xy2-4x2y-y3=-y(4x2-4xy+y2)=-y(2x-y)2.
(3)(a2+1)2-4a(a2+1)+4a2=(a2+1-2a)2 =(a2-2a+1)2=[(a-1)2]2=(a-1)4.
(4)(x2+y2)2-4x2y2=(x2+y2+2xy)(x2+y2-2xy)=(x+y)2(x-y)2.相关题1 把下列各式分解因式:
(1)5x2-15xy+10xy2;
(2)a(x-2)+(2-x)2;
(3)2x2y-8xy+8y;
(4)(m2+n2)2-4m2n2.【要点指导】应用公式a2-b2=(a+b)(a-b), a2±2ab+b2=(a±b)2先将所求的代数式进行变形, 再把相应的值代入计算. 专题二 因式分解与代数式的值例2 若|a+b-6|+(ab-4)2=0, 求-a3b-2a2b2-ab3的值.分析 根据非负数的性质得到a+b=6, ab=4, 将所求代数式进行因式分解, 然后整体代入求值. 解 ∵|a+b-6|+(ab-4)2=0,
∴a+b-6=0且ab-4=0, 则a+b=6, ab=4,
∴-a3b-2a2b2-ab3=-ab(a2+2ab+b2)=-ab(a+b)2=-4×62=-144. A相关题2-1 若x2-3x+2=0, 则x3-x2-4x+10的值是( ).
A.6 B.8 C.10 D.12解析 ∵x2-3x+2=0,∴x3-x2-4x+10=x3-3x2+2x+2x2-6x+4+6=
x(x2-3x+2)+2(x2-3x+2)+6=6.故选A相关题2-2 已知相邻边长分别为a, b的长方形, 它的周长为12, 面积为2, 则代数式a3b+2a2b2+ab3的值为________.72【要点指导】 将一个式子或一个式子的某一部分通过恒等变形为
完全平方式或几个完全平方式的和的形式, 这种方法称为配方法. 配方法常被用到式子的恒等变形中, 以挖掘题目中的隐含条件, 是解题的有力手段之一.专题三 配方法例3 已知4x2-20x+8y+y2+41=0, 求-xy的值.分析 观察所给等式左边的特点, 若将41拆成25与16两项, 则可以分组结合配方, 从而利用完全平方式的非负性解决问题.相关题3 求证:不论x取何实数, 多项式-2x4-12x3-18x2的值都不会是正数.【要点指导】 因式分解不仅在数值计算、代数式的化简求值等方面有广泛的应用, 在解决实际问题时也同样重要.通过学习和应用
因式分解, 能使我们的观察能力、运算能力、逻辑思维能力、探究
能力得到提高.专题四 因式分解的应用分析 由于题目中的数字较大, 考虑将分母中的20 212 0192+
20 212 0212-2写成20 212 0192-1+20 212 0212-1, 这样可以直接运用平方差公式进行因式分解, 再提取公因式后进行适当的数字变形即可求解. 相关题4 数学课上老师出了一道题:计算2962的值, 喜欢数学的小亮举手做出这道题, 他的解题过程如下:2962=(300-4)2=3002-2×
300×(-4)+42=90 000+2400+16=92 416.
老师表扬小亮积极发言的同时, 也指出了解题中的错误, 你认为小亮的解题过程错在哪儿, 并写出正确的解答过程.分析 先利用因式分解的方法求出广场铺草坪的面积为a2-4b2=
(a+2b)(a-2b), 再把a, b的值分别代入求出面积, 最后计算要投资的钱数. 例5 在一个边长为a=84 m的正方形广场的四角均留出一个边长为
b=8 m的正方形修建花坛, 其余地方铺草坪, 草坪的面积有多大?如果铺草坪每平方米需5元, 那么给这个广场铺草坪至少要投资多少元?解 广场铺草坪的面积为a2-4b2=(a+2b)(a-2b).
当a=84 m, b=8 m时, a2-4b2=(84+2×8)×(84-2×8)=100×68=6800(m2).
需投资的金额为5×6800=34 000(元).
故草坪的面积为6800 m2, 给这个广场铺草坪至少要投资34 000元.答案 3600 cm2【要点指导】用整体思想解数学题, 就是把一些看似彼此独立而实质是紧密关联的量看成一个整体去设元、列式、变形、消元、代入或求值等. 这样不仅可以摆脱固定模式的束缚, 使复杂的问题变得简单, 让陌生的问题变得熟悉, 往往还可以解决一些用常规方法解决不了的问题.专题 整体思想在因式分解中的应用例 因式分解:(xy-1)2+(x+y-2)(x+y-2xy).解 设x+y=a, xy=b,
则原式=(b-1)2+(a-2)(a-2b)=b2-2b+1+a2-2a+4b-2ab=(a2-2ab+b2)-
(2a-2b)+1=(a-b)2-2(a-b)+1=(a-b-1)2=(x+y-xy-1)2=(x-1)2(y-1)2.相关题 因式分解:
(1)(x+2y)2-2(x+2y)+1;
(2)(a+b)2-4(a+b-1);
(3)(x-1)(x-2)(x-3)(x-4)-120. 母题1 (教材P93随堂练习第2题)
下列由左边到右边的变形, 哪些是因式分解?为什么?
(1)(a+3)(a-3)=a2-9;
(2)m2-4=(m+2)(m-2);
(3)a2-b2+1=(a+b)(a-b)+1;
(4)2mR+2mr=2m(R+r).考点:因式分解的概念.
考情:因式分解的概念在中考中不常出现, 一般只以选择题、填空题的形式出现, 多以单独知识点的形式考查.
策略:因式分解是把一个多项式化为几个整式的积的形式.链接1 [滨州中考]下列各式从左到右的变形中, 属于因式分解的
是( ).
A.a(m+n)=am+an
B.a2-b2-c2=(a-b)(a+b)-c2
C.10x2-5x=5x(2x-1)
D.x2-16+6x=(x+4)(x-4)+6x分析 因式分解是把一个多项式化为几个整式的积的形式, 只有C选项满足, 故选C.答案 C母题2 (教材P104复习题第1题)
把下列各式因式分解:
(1)7x2-63; (2)a3-a; (3)3a2-3b2; (4)y2-9(x+y)2;
(5)a(x-y)-b(y-x)+c(x-y);
(6)x(m+n)-y(n+m)+(m+n);
(7)(x+y)2-16(x-y)2; (8)a2(a-b)2-b2(a-b)2;
(9)(x+y+z)2-(x-y-z)2; (10)(x+y)2-14(x+y)+49. 考点:因式分解.
考情:因式分解是中考的常考考点, 常以选择题、填空题的形式出现, 也会和其他知识点一起考查, 难度较小.
策略:若一个多项式有公因式, 则因式分解时应先提取公因式, 再用公式法进行因式分解, 注意因式分解要彻底, 分解到不能再分解为止.链接2 [泸州中考]分解 因 式 : 2 m 2- 8 =_______________.分析 先提取公因式, 再运用平方差公式分解.2m2-8=2(m2-4)=2(m+2)(m-2). 2(m+2)(m-2)链接3 [安徽中考]因式分解:a2b-4ab+4b= ___________ . 分析 a2b-4ab+4b=b(a2-4a+4)=b(a-2)2. b(a-2)2考点:利用因式分解求代数式的值.
考情:利用因式分解求代数式的值是中考的常考点, 题型比较灵活, 选择题、填空题、解答题都有出现.
策略:通过提公因式法、公式法把多项式变成含有已知条件的形式, 然后直接代入求值即可.链接5 [菏泽中考]已知4x=3y, 求代数式(x-2y)2-(x-y)(x+y)-2y2
的值.解 (x-2y)2-(x-y)(x+y)-2y2=(x2-4xy+4y2)-(x2-y2)-2y2
=x2-4xy+4y2-x2+y2-2y2=-4xy+3y2=-y(4x-3y).
因为4x=3y, 所以4x-3y=0,
所以原式=0.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
