北师大版 八年级数学下册第二章 一元一次不等式与一元一次不等式组章末复习课件(共60张)
文档属性
| 名称 | 北师大版 八年级数学下册第二章 一元一次不等式与一元一次不等式组章末复习课件(共60张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 13:18:13 | ||
图片预览











文档简介
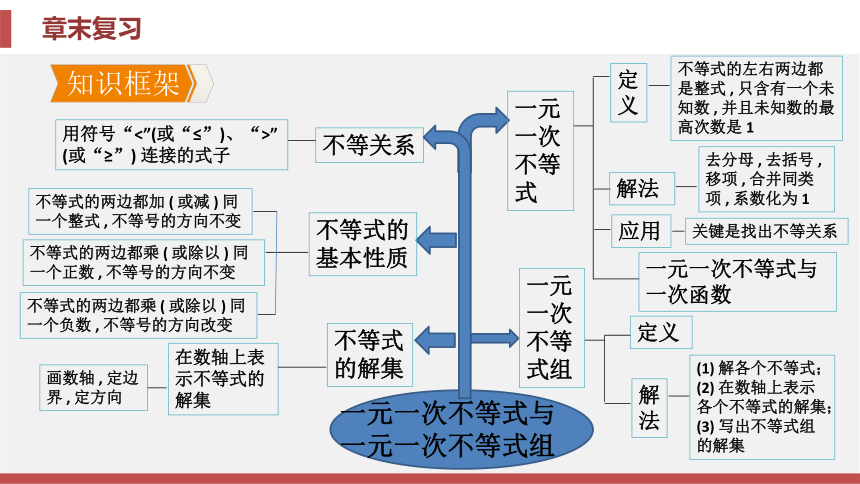
课件60张PPT。第二章 一元一次不等式
与一元一次不等式组章末复习第二章 一元一次不等式与一元一次不等式组章末复习【要点指导】不等式的基本性质是解一元一次不等式(组)及不等式
变形的主要依据. 不等式的两边都乘(或除以)同一个负数, 不等号的方向要改变. 当不能明确不等式两边同乘(或除以)的是正数还是负数时, 要分类讨论. 专题一 不等式的基本性质分析 根据不等式的基本性质3, 不等式两边都乘同一个负数时, 不等号的方向要改变, A, B选项中不等式的两边所乘的数不一样, 选项C中两边同乘-2, 但不等号的方向没有改变, 故A, B, C选项均错误.例1 若a>b, 则( ).
A.a>-b B.a<-b
C.-2a>-2b D.-2a<-2bD相关题1 下列不等式变形正确的是( ).
A.由a>b, 得ac>bc
B.由a>b, 得-2ac>-2bc
C.由a>b, 得-a>-b
D.由a>b, 得a-2>b-2D【要点指导】明确不等式的解与解集的区别, 用数轴表示不等式的
解集时, 要抓住两点:一是分界点, 二是方向. 解一元一次不等式组, 首先求出每个不等式的解集, 标在同一个数轴上, 取这些不等式解集的公共部分, 即不等式组的解集. 没有公共部分的, 则不等式组无解. 在求出不等式或不等式组的解集后, 既可解决该范围的有关整数解、正整数解等问题, 又可解决有关字母的值或取值范围等问题.专题二 一元一次不等式和一元一次不等式组的解法分析 应先去分母, 再移项、合并同类项, 最后把系数化为1. 解析 ①分别求出两个不等式的解集;②求两个不等式解集的公共部分;③在两个不等式解集的公共部分中确定整数解.【要点指导】 由已知不等式(组)的解集或整数解来确定未知字母的值或取值范围, 常用的方法是先用解不等式(组)的方法求出含未知字母的不等式(组)的解集, 再根据已给出的条件, 即可求出未知字母的值或取值范围.专题三 根据不等式(组)的解集确定字母的值(取值范围)分析 先求出不等式组的解集, 即x的取值范围, 然后根据不等式组的整数解的个数确定其整数解, 再借助数轴进行直观分析得到b的取值范围.答案 C-3≤a<-2【要点指导】 列不等式解应用题的一般步骤是通过分析复杂问题中的数量关系, 从而找出不等关系去解决实际问题, 即审题→设一个未知数→找出题中所有的数量关系, 列出不等式→解不等式→检验→作答.专题四 一元一次不等式的实际应用例4 为了举行班级晚会, 孔明准备去商店购买20个乒乓球做道具, 并买一些乒乓球拍做奖品. 已知乒乓球每个1.5元, 球拍每个22元, 如果购买金额不超过200元, 且买的球拍尽可能多, 那么孔明应该买多少个球拍?分析 由题意可得不等关系:购买乒乓球的花费+购买球拍的花≤200元, 由此可列不等式解决问题.相关题4 为加强中小学生安全和禁毒教育, 某校组织了“防溺水、交通安全、禁毒”知识竞赛, 为奖励在竞赛中表现优异的班级, 学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同, 每个篮球的价格相同). 已知购买1个足球和1个篮球共需159元;1个足球的价格比1个篮球的价格的2倍少9元.
(1)足球和篮球的单价各是多少?
(2)根据学校实际情况, 需一次性购买足球和篮球共20个, 但要求购买足球和篮球的总费用不超过1550元, 学校最多可以购买多少个足球?解析 (1)设足球的单价为x元/个,篮球的单价为y元/个.根据①1个足球费用+1个篮球费用=159元;②1个足球的价格比1个篮球的价格的2倍少9元列方程组求解即可;
(2)设购买足球m个,则购买篮球(20-m)个,根据购买足球和篮球的总费用不超过1550元建立不等式求出其解集即可.【要点指导】 当一次函数中一个变量的值确定时, 函数问题就转化为方程问题, 利用方程可以确定另一个变量的值;当已知函数中的一个变量的取值范围时, 函数问题就转化为不等式(组)的问题, 利用不等式(组)可以确定另一个变量的取值范围. 专题五 一次函数、一元一次方程及一元一次不等式的关系例5 在“美丽广西, 清洁乡村”活动中, 李家村村主任提出两种购买垃圾桶的方案. 方案1:买分类垃圾桶, 需要费用3000元, 以后每月的垃圾处理费用为250元;方案2:买不分类垃圾桶,需要费用1000元, 以后每月的垃圾处理费用为500元. 设方案1的购买费和每月垃圾处理费共y1元, 方案2的购买费和每月垃圾处理费共y2元, 交费时间为x个月.
(1)直接写出y1, y2与x之间的函数关系式(不必写出自变量的取值范围);(3)①由250x+3000<500x+1000, 得x>8,
所以当x>8时, 方案1省钱;
②由250x+3000=500x+1000, 得x=8,
所以当x=8时, 两种方案一样;
③由250x+3000>500x+1000, 得x<8,
所以当x<8时, 方案2省钱.(3)在(2)的解集中, 比较mx与kx+b的大小(直接写出结果).解 (1)x=2 x>0
(2)0<x<2
(3)当0当x=1时,mx=kx+b;
当1借助数轴的直观性确定相关字母或字母所在代数式的取值范围, 以及借助函数图像求解不等式(组)都体现了数形结合的思想. 在解决与数轴有关的问题时, 要注意空心圆圈与实心圆点的区别, 全面考虑问题.专题 数形结合思想答案 A答案 B母题1 (教材P41随堂练习第2题)
已知x>y, 下列不等式一定成立吗?
(1)x-6<y-6;(2)3x<3y;
(3)-2x<-2y;(4)2x+1>2y+1.考点:不等式的基本性质.
考情:考查不等式的基本性质的题目比较简单,多以选择题、填空题的形式出现, 常与整式的运算结合, 难度较小.
策略:理解不等式的基本性质:(1)不等式的两边都加(或减)同一个整式, 不等号的方向不变;(2)不等式的两边都乘(或除以)同一个正数, 不等号的方向不变;(3)不等式的两边都乘(或除以)同一个负数, 不等号的方向改变.答案 B考点:解一元一次不等式.
考情:解一元一次不等式一般与数轴的知识综合考查, 有关的选择题、填空题、解答题在中考中都有出现.
策略:解题步骤:去分母、去括号、移项、合并同类项、系数化为1. 注意去分母时, 不要漏乘不含分母的项.答案 B解 去分母, 得3(x-2)≤2(7-x).
去括号, 得3x-6≤14-2x.
移项, 得3x+2x≤14+6.
合并同类项, 得5x≤20.
两边都除以5, 得x≤4.考点:一元一次不等式组的解法.
考情:一元一次不等式组的解法是各地每年中考的热门考点, 是必考题. 常考查利用数轴表示其解集, 还会考查其整数解, 题型灵活, 与此有关的选择题、填空题、解答题在中考中都有出现.
策略:确定不等式组解集的口诀:同大取大, 同小取小, 大小小大中间找, 大大小小无处找.母题4 (教材P49随堂练习第1题)
某种商品的进价为400元, 出售时标价为500元,商店准备打折出售, 但要保持利润率不低于10%,则至多可打几折?考点:一元一次不等式的应用.
考情:一元一次不等式的应用在近几年的中考中考查较多, 其中少数以选择题、填空题的形式出现, 更多的是在解答题中与方程或方程组综合在一起考查.
策略:理解题意, 找出不等关系并根据题目的实际意义列出不等式.链接5 [辽阳中考]青年志愿者爱心小分队赴山村送温暖, 准备为困难村民购买一些米面. 已知购买1袋大米、4袋面粉, 共需240元;购买2袋大米、1袋面粉, 共需165元.
(1)求每袋大米和面粉各多少元;
(2)如果爱心小分队计划购买这些米面共40袋,
总费用不超过2140元, 那么至少购买多少袋面粉?(2)最省钱的购买方案为购买A种商品8件, B种商品4件.
理由:设第三次购买B种商品a件, 则购买A种商品(12-a)件. 根据题意, 得12-a≥2a, 解得a≤4, 则8≤12-a≤12.
∵A种商品的单价高于B种商品的单价,
∴B种商品购买得越多花费越少, 则a=4, 即购买A种商品8件, 购买B种商品4件时, 总花费最少, 最少为20×8+15×4=220(元).母题5(教材P53习题2.7第1题)
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元, 另收3000元设计费;乙公司提出:每份材料收费30元, 不收设计费.
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?考点:一元一次不等式与一次函数的综合运用.
考情:一元一次不等式与一次函数的综合运用是中考的常考题, 与此有关的选择题、填空题、解答题都有出现.
策略:先根据两个函数图像的交点, 确定出横坐标的值, 再利用数形结合思想得出不等式的解集.
谢 谢 观 看!
与一元一次不等式组章末复习第二章 一元一次不等式与一元一次不等式组章末复习【要点指导】不等式的基本性质是解一元一次不等式(组)及不等式
变形的主要依据. 不等式的两边都乘(或除以)同一个负数, 不等号的方向要改变. 当不能明确不等式两边同乘(或除以)的是正数还是负数时, 要分类讨论. 专题一 不等式的基本性质分析 根据不等式的基本性质3, 不等式两边都乘同一个负数时, 不等号的方向要改变, A, B选项中不等式的两边所乘的数不一样, 选项C中两边同乘-2, 但不等号的方向没有改变, 故A, B, C选项均错误.例1 若a>b, 则( ).
A.a>-b B.a<-b
C.-2a>-2b D.-2a<-2bD相关题1 下列不等式变形正确的是( ).
A.由a>b, 得ac>bc
B.由a>b, 得-2ac>-2bc
C.由a>b, 得-a>-b
D.由a>b, 得a-2>b-2D【要点指导】明确不等式的解与解集的区别, 用数轴表示不等式的
解集时, 要抓住两点:一是分界点, 二是方向. 解一元一次不等式组, 首先求出每个不等式的解集, 标在同一个数轴上, 取这些不等式解集的公共部分, 即不等式组的解集. 没有公共部分的, 则不等式组无解. 在求出不等式或不等式组的解集后, 既可解决该范围的有关整数解、正整数解等问题, 又可解决有关字母的值或取值范围等问题.专题二 一元一次不等式和一元一次不等式组的解法分析 应先去分母, 再移项、合并同类项, 最后把系数化为1. 解析 ①分别求出两个不等式的解集;②求两个不等式解集的公共部分;③在两个不等式解集的公共部分中确定整数解.【要点指导】 由已知不等式(组)的解集或整数解来确定未知字母的值或取值范围, 常用的方法是先用解不等式(组)的方法求出含未知字母的不等式(组)的解集, 再根据已给出的条件, 即可求出未知字母的值或取值范围.专题三 根据不等式(组)的解集确定字母的值(取值范围)分析 先求出不等式组的解集, 即x的取值范围, 然后根据不等式组的整数解的个数确定其整数解, 再借助数轴进行直观分析得到b的取值范围.答案 C-3≤a<-2【要点指导】 列不等式解应用题的一般步骤是通过分析复杂问题中的数量关系, 从而找出不等关系去解决实际问题, 即审题→设一个未知数→找出题中所有的数量关系, 列出不等式→解不等式→检验→作答.专题四 一元一次不等式的实际应用例4 为了举行班级晚会, 孔明准备去商店购买20个乒乓球做道具, 并买一些乒乓球拍做奖品. 已知乒乓球每个1.5元, 球拍每个22元, 如果购买金额不超过200元, 且买的球拍尽可能多, 那么孔明应该买多少个球拍?分析 由题意可得不等关系:购买乒乓球的花费+购买球拍的花≤200元, 由此可列不等式解决问题.相关题4 为加强中小学生安全和禁毒教育, 某校组织了“防溺水、交通安全、禁毒”知识竞赛, 为奖励在竞赛中表现优异的班级, 学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同, 每个篮球的价格相同). 已知购买1个足球和1个篮球共需159元;1个足球的价格比1个篮球的价格的2倍少9元.
(1)足球和篮球的单价各是多少?
(2)根据学校实际情况, 需一次性购买足球和篮球共20个, 但要求购买足球和篮球的总费用不超过1550元, 学校最多可以购买多少个足球?解析 (1)设足球的单价为x元/个,篮球的单价为y元/个.根据①1个足球费用+1个篮球费用=159元;②1个足球的价格比1个篮球的价格的2倍少9元列方程组求解即可;
(2)设购买足球m个,则购买篮球(20-m)个,根据购买足球和篮球的总费用不超过1550元建立不等式求出其解集即可.【要点指导】 当一次函数中一个变量的值确定时, 函数问题就转化为方程问题, 利用方程可以确定另一个变量的值;当已知函数中的一个变量的取值范围时, 函数问题就转化为不等式(组)的问题, 利用不等式(组)可以确定另一个变量的取值范围. 专题五 一次函数、一元一次方程及一元一次不等式的关系例5 在“美丽广西, 清洁乡村”活动中, 李家村村主任提出两种购买垃圾桶的方案. 方案1:买分类垃圾桶, 需要费用3000元, 以后每月的垃圾处理费用为250元;方案2:买不分类垃圾桶,需要费用1000元, 以后每月的垃圾处理费用为500元. 设方案1的购买费和每月垃圾处理费共y1元, 方案2的购买费和每月垃圾处理费共y2元, 交费时间为x个月.
(1)直接写出y1, y2与x之间的函数关系式(不必写出自变量的取值范围);(3)①由250x+3000<500x+1000, 得x>8,
所以当x>8时, 方案1省钱;
②由250x+3000=500x+1000, 得x=8,
所以当x=8时, 两种方案一样;
③由250x+3000>500x+1000, 得x<8,
所以当x<8时, 方案2省钱.(3)在(2)的解集中, 比较mx与kx+b的大小(直接写出结果).解 (1)x=2 x>0
(2)0<x<2
(3)当0
当1
已知x>y, 下列不等式一定成立吗?
(1)x-6<y-6;(2)3x<3y;
(3)-2x<-2y;(4)2x+1>2y+1.考点:不等式的基本性质.
考情:考查不等式的基本性质的题目比较简单,多以选择题、填空题的形式出现, 常与整式的运算结合, 难度较小.
策略:理解不等式的基本性质:(1)不等式的两边都加(或减)同一个整式, 不等号的方向不变;(2)不等式的两边都乘(或除以)同一个正数, 不等号的方向不变;(3)不等式的两边都乘(或除以)同一个负数, 不等号的方向改变.答案 B考点:解一元一次不等式.
考情:解一元一次不等式一般与数轴的知识综合考查, 有关的选择题、填空题、解答题在中考中都有出现.
策略:解题步骤:去分母、去括号、移项、合并同类项、系数化为1. 注意去分母时, 不要漏乘不含分母的项.答案 B解 去分母, 得3(x-2)≤2(7-x).
去括号, 得3x-6≤14-2x.
移项, 得3x+2x≤14+6.
合并同类项, 得5x≤20.
两边都除以5, 得x≤4.考点:一元一次不等式组的解法.
考情:一元一次不等式组的解法是各地每年中考的热门考点, 是必考题. 常考查利用数轴表示其解集, 还会考查其整数解, 题型灵活, 与此有关的选择题、填空题、解答题在中考中都有出现.
策略:确定不等式组解集的口诀:同大取大, 同小取小, 大小小大中间找, 大大小小无处找.母题4 (教材P49随堂练习第1题)
某种商品的进价为400元, 出售时标价为500元,商店准备打折出售, 但要保持利润率不低于10%,则至多可打几折?考点:一元一次不等式的应用.
考情:一元一次不等式的应用在近几年的中考中考查较多, 其中少数以选择题、填空题的形式出现, 更多的是在解答题中与方程或方程组综合在一起考查.
策略:理解题意, 找出不等关系并根据题目的实际意义列出不等式.链接5 [辽阳中考]青年志愿者爱心小分队赴山村送温暖, 准备为困难村民购买一些米面. 已知购买1袋大米、4袋面粉, 共需240元;购买2袋大米、1袋面粉, 共需165元.
(1)求每袋大米和面粉各多少元;
(2)如果爱心小分队计划购买这些米面共40袋,
总费用不超过2140元, 那么至少购买多少袋面粉?(2)最省钱的购买方案为购买A种商品8件, B种商品4件.
理由:设第三次购买B种商品a件, 则购买A种商品(12-a)件. 根据题意, 得12-a≥2a, 解得a≤4, 则8≤12-a≤12.
∵A种商品的单价高于B种商品的单价,
∴B种商品购买得越多花费越少, 则a=4, 即购买A种商品8件, 购买B种商品4件时, 总花费最少, 最少为20×8+15×4=220(元).母题5(教材P53习题2.7第1题)
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元, 另收3000元设计费;乙公司提出:每份材料收费30元, 不收设计费.
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?考点:一元一次不等式与一次函数的综合运用.
考情:一元一次不等式与一次函数的综合运用是中考的常考题, 与此有关的选择题、填空题、解答题都有出现.
策略:先根据两个函数图像的交点, 确定出横坐标的值, 再利用数形结合思想得出不等式的解集.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
