北师大版 八年级数学下册第三章 图形的平移与旋转章末复习课件(共51张)
文档属性
| 名称 | 北师大版 八年级数学下册第三章 图形的平移与旋转章末复习课件(共51张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览








文档简介
课件51张PPT。第三章 图形的平移
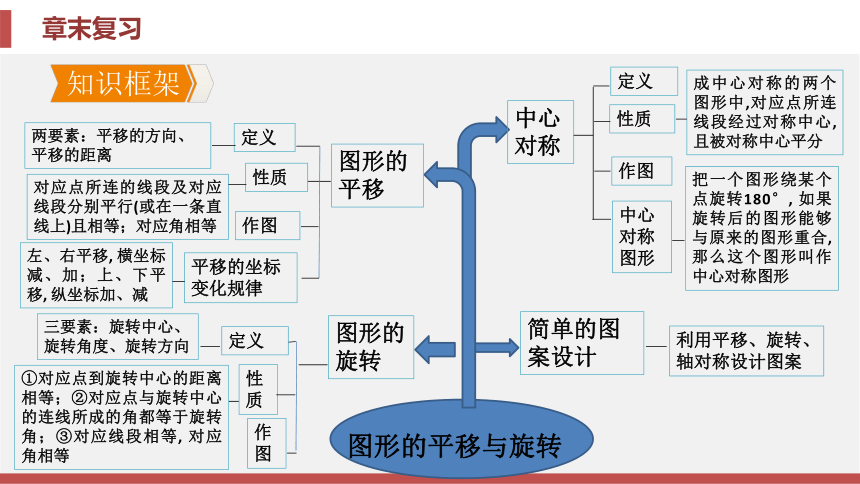
与旋转章末复习第三章 图形的平移与旋转章末复习知识框架归纳整合素养提升中考链接知识框架【要点指导】平移作为一种基本的几何变换, 它是研究几何问题的有效工具, 平移往往与面积、变换性质相联系, 与画图、测量、猜想、
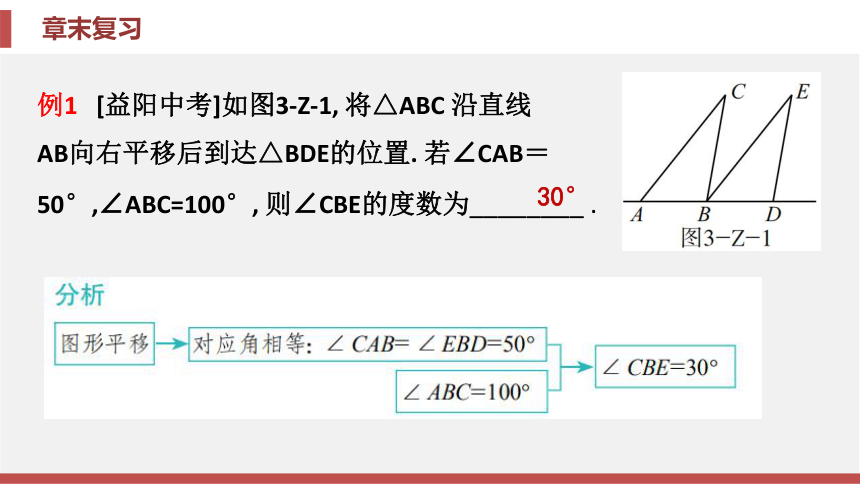
探究、证明等探索问题相关. 常利用平移设计图案和分析解决生活中的问题, 为此要树立平移变换思想, 熟练掌握平移的性质. 归纳整合专题一 运用平移的特征进行简单的作图、计算、设计与应用例1 [益阳中考]如图3-Z-1, 将△ABC 沿直线
AB向右平移后到达△BDE的位置. 若∠CAB=
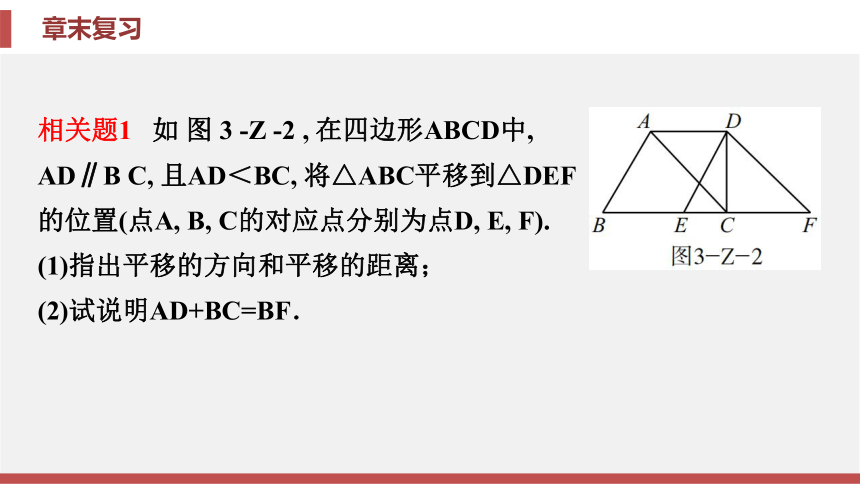
50°,∠ABC=100°, 则∠CBE的度数为________ . 30°相关题1 如 图 3 -Z -2 , 在四边形ABCD中,
AD∥B C, 且AD<BC, 将△ABC平移到△DEF
的位置(点A, B, C的对应点分别为点D, E, F).
(1)指出平移的方向和平移的距离;
(2)试说明AD+BC=BF.解:(1)平移的方向是点A到点D(或点B到点E或点C到点F)的方向,平移的距离是线段AD(或线段BE或线段CF)的长度.
(2)∵△ABC平移到△DEF的位置,
∴CF=AD.
由题意易得点B,E,C,F在同一条直线上.
∵CF+BC=BF,
∴AD+BC=BF.【要点指导】要把握好旋转的三要素:旋转中心、旋转角度和旋
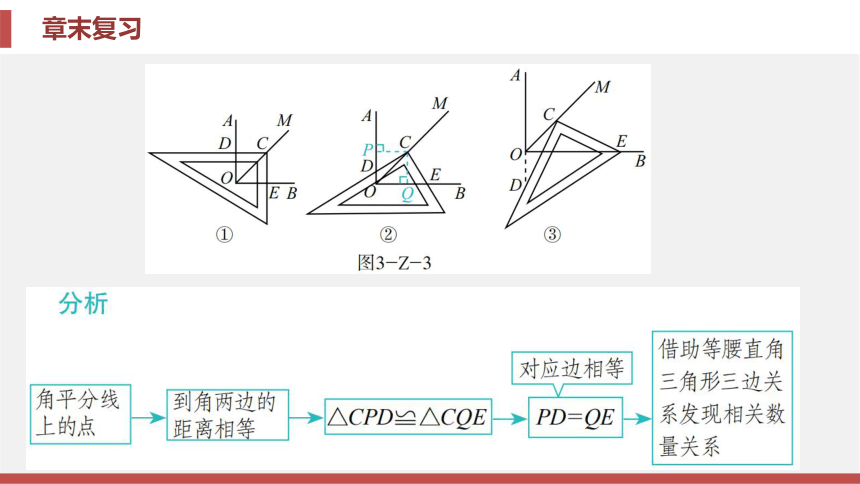
转方向, 从而发现相关几何图形的性质及结论并进行相关的计算、证明与探究. 对于图形的旋转变换(性质), 以及在变换过程中的不变量、变化量要引起高度重视.必要时进行动手操作与实验, 运用转化与化归的数学思想进行分析与探究, 捕捉某些特殊图形或位置, 化一般为特殊.专题二 运用旋转的特征进行简单的作图、计算、设计与应用例2 已知∠AOB=90°, 在∠AOB的平分线OM上有一点C, 将一个三角尺的直角顶点与点C重合, 它的两条直角边分别与OA, OB(或它们的反向延长线)相交于点D, E. 当三角尺绕点C旋转到CD与OA垂直时, 如图3-Z-3①, 易证OD+OE= OC. 当三角尺绕点C旋转到CD与OA不垂直时, 在图②③这两种情况下, 上述结论是否还成立?若成立, 请给予证明;若不成立, 线段OD, OE, OC之间又有怎样的数量关系?请写出你的猜想, 不需要证明. 解 在图②中, 结论还成立;在图③中, 结论不成立. 图②结论:
OD+OE= OC.
证明如下:过点C分别作OA, OB的垂线, 垂足分别为P, Q,
如图②, 易证△CPD≌△CQE, ∴PD=QE. 又∵OP=OD+PD, OQ=OE-QE,
且OP+OQ= OC, 即OD+PD+OE-QE= OC,
∴ OD+OE= OC.
图③结论:OE-OD= OC. 4π相关题2-1 如图3 -Z -4, AB是长为8 cm的线段,
且CD⊥AB于点O, 则图中阴影部分的面积是
________cm2.解析 观察图形的特点,本题可借助旋转的性质来求解.不妨将最小的和较小的两块阴影分别绕点O逆时针旋转180°和90°,这样将这些分散的阴影部分集中在一起构成一个半径为4 cm的圆的,由此可得阴影部分的面积为4π cm2.相关题2-2 [荆门中考]如图3-Z-5, 在Rt△ABC中, ∠ACB=90°,点D, E分别在AB, AC上,EC=BC, 连
接CD, 将线段CD绕点C按顺时针方向旋转90°后
得CF, 连接EF.
(1)将图形补充完整;
(2)若EF∥CD, 求证:∠BDC=90°.解 :(1)补全图形,如图所示.
(2)证明:由旋转得∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD.
∵EF∥CD,∴∠EFC+∠DCF=180°,∴∠EFC=90°.
在△BDC和△EFC中,∵DC=FC,∠BCD=∠ECF,BC=EC,
∴△BDC≌△EFC(SAS),∴∠BDC=∠EFC=90°.【要点指导】 图形变换是初中数学的重要内容, 网格中的图形变换
将代数与几何有机结合, 体会数与形的关系, 充分利用图形变换解决数学问题.专题三 网格中的图形变换例3 如图3-Z-6, 每个小方格都是边长为1个单位
长度的小正方形.
(1)将△ABC向右平移3个单位长度, 画出平移后
的△A1B1C1;
(2)将△ABC绕点O旋转180°, 画出旋转后的
△A2B2C2;
(3)画出一条直线将△AC1A2的面积分成相等的两部分. 分析 (1)分别将△ABC的顶点A, B, C向右平移3个单位长度, 连接所
得的点即可得出图形;
(2)分别将△ABC的顶点A, B, C绕点O旋转180°, 连接所得的点即可得出图形;
(3)连接OC1, 即可平分△AC1A2的面积.解 (1)(2)如图3-Z-7所示.
(3)面积等分正确即可, 如图3-Z-7所示, 直线
OC1将△AC1A2的面积分成相等的两部分
(答案不唯一).相关题3 在如图3-Z-8所示的方格图中(每个小正
方形的边长为1个单位长度), 我们称每个小正方
形的顶点为“格点”, 以格点为顶点的三角形叫
作“格点三角形”, 根据图形, 回答下列问题:
(1)图中格点三角形A' B' C'是由格点三角形ABC
通过怎样的变换得到的?
(2)建立如图所示的平面直角坐标系, 如果点A的坐标为(-3, 4), 请写出格点三角形DEF各顶点的坐标, 并求出△DEF的面积.【要点指导】有关全等变换对应的坐标变化规律的问题, 一般根据图形的运动方式, 求点的坐标, 或根据点的坐标确定图形的运动方式. 解决此类题需要熟练掌握图形变换对应的坐标变化规律, 能将数形有机结合起来, 并能做到灵活转换, 快捷地解决问题.素养提升专题 数形结合思想例 [菏泽中考]如图3-Z-9, 点A, B的坐标分
别为(2, 0), (0, 1). 若将线段AB平移至A1B1的
位置, 则a+b的值为( ).
A.2 B.3 C.4 D.5分析 由点B平移前后的纵坐标分别为1, 2, 可得点B向上平移了1个单位长度, 由点A平移前后的横坐标分别为2, 3, 可得点A向右平移了1个单位长度, 由此得线段AB的平移过程是向上平移了1个单位长度, 向右平移了1个单位长度, 所以点A, B均按此规律平移, 由此可得a=0+1=1, b=0+1=1, 故a+b=2. 答案 A相关题 [随州中考]在平面直角坐标系中, 将点(-2, 3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( ).
A.(4, -3) B.(-4, 3)
C.(0, -3) D.(0, 3)解析 点(-2,3)关于原点的对称点是(2,-3),将其向左平移2个单位长度得到的点的坐标是(0,-3).故选C.C中考链接母题1 (教材P83随堂练习第1题)
下面哪些图形是中心对称图形?考点:轴对称图形、中心对称图形.
考情:图形的识别是中考常考的内容, 大多以选择题的形式出现, 属于基础题.
策略:根据定义来识别. 轴对称图形:如果一个图形沿一条直线折叠后, 直线两旁的部分能够互相重合, 那么这个图形就是轴对称图形;中心对称图形:在平面内, 把一个图形绕某个点旋转180°, 如果旋转后的图形能与原来的图形重合,那么这个图形就是中心对称图形.链接1 [德州中考]下列图形中, 是中心对称图形但不是轴对称图形的是( ).答案 B母题2 (教材P77随堂练习第1题)
如图3 - Z - 1 2 , 四边形ABCD经过旋转后与四边形
ADEF重合.
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角.考点:图形变换性质的应用.
考情:平移和旋转的性质是近几年中考常考内容, 选择题、填空题、解答题的形式都有出现,常与线段、三角形、四边形等图形相结合进行综合考查.
策略:观察图形, 分析对应线段、对应点、对应角, 熟知平移、旋转前后的图形是全等形是解答此类题的关键.链接2 [哈尔滨中考]如图3-Z-13, 在Rt△ABC
中, ∠BAC=90°, ∠B=60°,△AB′C′可以由
△ABC绕点A顺时针旋转90°得到(点B′与点
B是对应点, 点C′与点C是对应点), 连接CC′,
则∠CC′B′的度数是( ).
A.45° B.30° C.25° D.15°答案 B链接3 [达州中考]如图3-Z-14, P是等边三角
形ABC内一点, 将线段AP绕点A顺时针旋转60°
得到线段AQ, 连接BQ. 若PA=6, PB=8, PC=10,
则四边形APBQ的面积为________ . 分析 如图3-Z-14, 连接PQ, 由旋转的性质可得△PAQ是等边三角形;利用全等三角形及勾股定理的逆定理易证△BPQ是直角三角形;分别求出两个三角形的面积可得四边形APBQ的面积.具体的解题过程如下:连接PQ, 如图3-Z-14.
由旋转的性质知PA=AQ, ∠PAQ=60°,
∴△PAQ是等边三角形,
∴PQ=PA=6, ∴S△PAQ= ×6×3 =9 .
∵∠CAB=∠PAQ=60°,∴∠CAP=∠BAQ.
又∵AC=AB, AP=AQ,∴△ACP≌△ABQ,∴BQ=PC=10.
∵PB=8, PQ=6, BQ=10,∴△BPQ是直角三角形, 且∠BPQ=90°,
∴S△BPQ= ×6×8=24, ∴S四边形APBQ=24+9 .故填24+9 . 答案 24+9母题3 (教材P73习题3.3第1题)
(1)在平面直角坐标系中描出点A(-8, 7), B(-7,3), C(-6, 7), D(-5, 3), E(-4, 7), 并将它们依次连接;
(2)将(1)中所画图形先向右平移10个单位长度, 再向下平移10个单位长度, 画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所画图形?平移前后对应点的横坐标有什么关系?纵坐标呢?考点:平移作图.
考情:平移作图是中考中的常考内容, 考查形式多样, 选择题、填空题、解答题皆有出现, 考查背景一般为平面直角坐标系或方格纸.
策略:网格内的平移作图一般利用数网格的方式进行. 平面直角坐标系内的平移作图一般利用平移变换对应的坐标变化规律进行. 链接4 [桂林中考]如图3-Z-15, 在网格中, 每个
小正方形的边长均为1个单位长度, 我们将小正
方形的顶点叫作格点, 线段AB的端点均在格点上.
(1)将线段AB向右平移3个单位长度, 得到线段
A′B′, 画出平移后的线段并连接AB′和A′B, 两线
段相交于点O;
(2)求证:△AOB≌△B′OA′.解 (1)如图3-Z-16所示.
(2)证明:由平移的性质, 得AB∥A′B′, AB=A′B′,
∴∠BAO=∠A′B′O, ∠ABO=∠B′A′O.
在△AOB和△B′OA′中,
∵∠BAO=∠A′B′O, AB=B′A′, ∠ABO=∠B′A′O,
∴△AOB≌△B′OA′.母题4 (教材P80习题3.5第3题)
如图3-Z-17, 你能对(甲)图案进行适当的运动变化, 使它与(乙)图案重合吗?写出你的操作过程.考点:旋转作图.
考情:旋转作图是近几年中考的常考内容, 以解答题的形式出现, 常与轴对称、中心对称等相结合在网格或平面直角坐标系中考查.
策略:旋转作图的关键是确定原图形上的关键点及其关于旋转中心的对称点.链接5 [丹东中考]在平面直角坐标系中,
△ABC的位置如图3-Z-18所示(每个小方格
都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长
度, 画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°, 画出
旋转后得到的△AB2C2, 并直接写出点B2, C2
的坐标.分析 (1)利用点平移的规律写出点A, B, C的对应点A1, B1, C1的坐标, 然后描点并连线即可得到△A1B1C1;
(2)利用网格特点和旋转的性质描出点B, C的对应点B2, C2, 从而得到△AB2C2, 再写出点B2, C2的坐标.解 (1)如图3-Z-19, △A1B1C1即为所求;
(2)如图3-Z-19, △AB2C2即为所求, 点B2(4,-2), C2(1, -3).母题5(教材P86习题3.7第1题)
利用旋转分析下列图案, 并设计一个你喜欢的徽标.考点:图案设计.
考情:利用平移、轴对称或中心对称进行图案设计是中考的非重点考点, 但近几年在某些地方中考中的分量逐渐增加, 选择题、填空题、解答题的形式都有出现, 常利用网格图进行考查.
策略:灵活运用图形的平移、旋转及轴对称的知识进行实际操作是解题的关键. 链接6 [宁波中考]图3-Z-21中的网格都是由9个相同的小正方形组成的, 每个网格图中有3个小正方形已涂上阴影, 请在余下的6个空白小正方形中, 按下列要求涂上阴影:
(1)选取1个涂上阴影, 使4个阴影小正方形组成一个轴对称图形, 但不是中心对称图形;
(2)选取1个涂上阴影, 使4个阴影小正方形组成一个中心对称图形, 但不是轴对称图形;(3)选取2个涂上阴影, 使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图①、图②、图③中, 均只需画出符合条件的一种情形)解 (1)答案不唯一, 如图3-Z-22, 画出其中一种即可. (2)答案不唯一, 如图3-Z-23, 画出其中一种即可.(3)答案不唯一, 如图3-Z-24, 画出其中一种即可.
谢 谢 观 看!
与旋转章末复习第三章 图形的平移与旋转章末复习知识框架归纳整合素养提升中考链接知识框架【要点指导】平移作为一种基本的几何变换, 它是研究几何问题的有效工具, 平移往往与面积、变换性质相联系, 与画图、测量、猜想、
探究、证明等探索问题相关. 常利用平移设计图案和分析解决生活中的问题, 为此要树立平移变换思想, 熟练掌握平移的性质. 归纳整合专题一 运用平移的特征进行简单的作图、计算、设计与应用例1 [益阳中考]如图3-Z-1, 将△ABC 沿直线
AB向右平移后到达△BDE的位置. 若∠CAB=
50°,∠ABC=100°, 则∠CBE的度数为________ . 30°相关题1 如 图 3 -Z -2 , 在四边形ABCD中,
AD∥B C, 且AD<BC, 将△ABC平移到△DEF
的位置(点A, B, C的对应点分别为点D, E, F).
(1)指出平移的方向和平移的距离;
(2)试说明AD+BC=BF.解:(1)平移的方向是点A到点D(或点B到点E或点C到点F)的方向,平移的距离是线段AD(或线段BE或线段CF)的长度.
(2)∵△ABC平移到△DEF的位置,
∴CF=AD.
由题意易得点B,E,C,F在同一条直线上.
∵CF+BC=BF,
∴AD+BC=BF.【要点指导】要把握好旋转的三要素:旋转中心、旋转角度和旋
转方向, 从而发现相关几何图形的性质及结论并进行相关的计算、证明与探究. 对于图形的旋转变换(性质), 以及在变换过程中的不变量、变化量要引起高度重视.必要时进行动手操作与实验, 运用转化与化归的数学思想进行分析与探究, 捕捉某些特殊图形或位置, 化一般为特殊.专题二 运用旋转的特征进行简单的作图、计算、设计与应用例2 已知∠AOB=90°, 在∠AOB的平分线OM上有一点C, 将一个三角尺的直角顶点与点C重合, 它的两条直角边分别与OA, OB(或它们的反向延长线)相交于点D, E. 当三角尺绕点C旋转到CD与OA垂直时, 如图3-Z-3①, 易证OD+OE= OC. 当三角尺绕点C旋转到CD与OA不垂直时, 在图②③这两种情况下, 上述结论是否还成立?若成立, 请给予证明;若不成立, 线段OD, OE, OC之间又有怎样的数量关系?请写出你的猜想, 不需要证明. 解 在图②中, 结论还成立;在图③中, 结论不成立. 图②结论:
OD+OE= OC.
证明如下:过点C分别作OA, OB的垂线, 垂足分别为P, Q,
如图②, 易证△CPD≌△CQE, ∴PD=QE. 又∵OP=OD+PD, OQ=OE-QE,
且OP+OQ= OC, 即OD+PD+OE-QE= OC,
∴ OD+OE= OC.
图③结论:OE-OD= OC. 4π相关题2-1 如图3 -Z -4, AB是长为8 cm的线段,
且CD⊥AB于点O, 则图中阴影部分的面积是
________cm2.解析 观察图形的特点,本题可借助旋转的性质来求解.不妨将最小的和较小的两块阴影分别绕点O逆时针旋转180°和90°,这样将这些分散的阴影部分集中在一起构成一个半径为4 cm的圆的,由此可得阴影部分的面积为4π cm2.相关题2-2 [荆门中考]如图3-Z-5, 在Rt△ABC中, ∠ACB=90°,点D, E分别在AB, AC上,EC=BC, 连
接CD, 将线段CD绕点C按顺时针方向旋转90°后
得CF, 连接EF.
(1)将图形补充完整;
(2)若EF∥CD, 求证:∠BDC=90°.解 :(1)补全图形,如图所示.
(2)证明:由旋转得∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD.
∵EF∥CD,∴∠EFC+∠DCF=180°,∴∠EFC=90°.
在△BDC和△EFC中,∵DC=FC,∠BCD=∠ECF,BC=EC,
∴△BDC≌△EFC(SAS),∴∠BDC=∠EFC=90°.【要点指导】 图形变换是初中数学的重要内容, 网格中的图形变换
将代数与几何有机结合, 体会数与形的关系, 充分利用图形变换解决数学问题.专题三 网格中的图形变换例3 如图3-Z-6, 每个小方格都是边长为1个单位
长度的小正方形.
(1)将△ABC向右平移3个单位长度, 画出平移后
的△A1B1C1;
(2)将△ABC绕点O旋转180°, 画出旋转后的
△A2B2C2;
(3)画出一条直线将△AC1A2的面积分成相等的两部分. 分析 (1)分别将△ABC的顶点A, B, C向右平移3个单位长度, 连接所
得的点即可得出图形;
(2)分别将△ABC的顶点A, B, C绕点O旋转180°, 连接所得的点即可得出图形;
(3)连接OC1, 即可平分△AC1A2的面积.解 (1)(2)如图3-Z-7所示.
(3)面积等分正确即可, 如图3-Z-7所示, 直线
OC1将△AC1A2的面积分成相等的两部分
(答案不唯一).相关题3 在如图3-Z-8所示的方格图中(每个小正
方形的边长为1个单位长度), 我们称每个小正方
形的顶点为“格点”, 以格点为顶点的三角形叫
作“格点三角形”, 根据图形, 回答下列问题:
(1)图中格点三角形A' B' C'是由格点三角形ABC
通过怎样的变换得到的?
(2)建立如图所示的平面直角坐标系, 如果点A的坐标为(-3, 4), 请写出格点三角形DEF各顶点的坐标, 并求出△DEF的面积.【要点指导】有关全等变换对应的坐标变化规律的问题, 一般根据图形的运动方式, 求点的坐标, 或根据点的坐标确定图形的运动方式. 解决此类题需要熟练掌握图形变换对应的坐标变化规律, 能将数形有机结合起来, 并能做到灵活转换, 快捷地解决问题.素养提升专题 数形结合思想例 [菏泽中考]如图3-Z-9, 点A, B的坐标分
别为(2, 0), (0, 1). 若将线段AB平移至A1B1的
位置, 则a+b的值为( ).
A.2 B.3 C.4 D.5分析 由点B平移前后的纵坐标分别为1, 2, 可得点B向上平移了1个单位长度, 由点A平移前后的横坐标分别为2, 3, 可得点A向右平移了1个单位长度, 由此得线段AB的平移过程是向上平移了1个单位长度, 向右平移了1个单位长度, 所以点A, B均按此规律平移, 由此可得a=0+1=1, b=0+1=1, 故a+b=2. 答案 A相关题 [随州中考]在平面直角坐标系中, 将点(-2, 3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( ).
A.(4, -3) B.(-4, 3)
C.(0, -3) D.(0, 3)解析 点(-2,3)关于原点的对称点是(2,-3),将其向左平移2个单位长度得到的点的坐标是(0,-3).故选C.C中考链接母题1 (教材P83随堂练习第1题)
下面哪些图形是中心对称图形?考点:轴对称图形、中心对称图形.
考情:图形的识别是中考常考的内容, 大多以选择题的形式出现, 属于基础题.
策略:根据定义来识别. 轴对称图形:如果一个图形沿一条直线折叠后, 直线两旁的部分能够互相重合, 那么这个图形就是轴对称图形;中心对称图形:在平面内, 把一个图形绕某个点旋转180°, 如果旋转后的图形能与原来的图形重合,那么这个图形就是中心对称图形.链接1 [德州中考]下列图形中, 是中心对称图形但不是轴对称图形的是( ).答案 B母题2 (教材P77随堂练习第1题)
如图3 - Z - 1 2 , 四边形ABCD经过旋转后与四边形
ADEF重合.
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角.考点:图形变换性质的应用.
考情:平移和旋转的性质是近几年中考常考内容, 选择题、填空题、解答题的形式都有出现,常与线段、三角形、四边形等图形相结合进行综合考查.
策略:观察图形, 分析对应线段、对应点、对应角, 熟知平移、旋转前后的图形是全等形是解答此类题的关键.链接2 [哈尔滨中考]如图3-Z-13, 在Rt△ABC
中, ∠BAC=90°, ∠B=60°,△AB′C′可以由
△ABC绕点A顺时针旋转90°得到(点B′与点
B是对应点, 点C′与点C是对应点), 连接CC′,
则∠CC′B′的度数是( ).
A.45° B.30° C.25° D.15°答案 B链接3 [达州中考]如图3-Z-14, P是等边三角
形ABC内一点, 将线段AP绕点A顺时针旋转60°
得到线段AQ, 连接BQ. 若PA=6, PB=8, PC=10,
则四边形APBQ的面积为________ . 分析 如图3-Z-14, 连接PQ, 由旋转的性质可得△PAQ是等边三角形;利用全等三角形及勾股定理的逆定理易证△BPQ是直角三角形;分别求出两个三角形的面积可得四边形APBQ的面积.具体的解题过程如下:连接PQ, 如图3-Z-14.
由旋转的性质知PA=AQ, ∠PAQ=60°,
∴△PAQ是等边三角形,
∴PQ=PA=6, ∴S△PAQ= ×6×3 =9 .
∵∠CAB=∠PAQ=60°,∴∠CAP=∠BAQ.
又∵AC=AB, AP=AQ,∴△ACP≌△ABQ,∴BQ=PC=10.
∵PB=8, PQ=6, BQ=10,∴△BPQ是直角三角形, 且∠BPQ=90°,
∴S△BPQ= ×6×8=24, ∴S四边形APBQ=24+9 .故填24+9 . 答案 24+9母题3 (教材P73习题3.3第1题)
(1)在平面直角坐标系中描出点A(-8, 7), B(-7,3), C(-6, 7), D(-5, 3), E(-4, 7), 并将它们依次连接;
(2)将(1)中所画图形先向右平移10个单位长度, 再向下平移10个单位长度, 画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所画图形?平移前后对应点的横坐标有什么关系?纵坐标呢?考点:平移作图.
考情:平移作图是中考中的常考内容, 考查形式多样, 选择题、填空题、解答题皆有出现, 考查背景一般为平面直角坐标系或方格纸.
策略:网格内的平移作图一般利用数网格的方式进行. 平面直角坐标系内的平移作图一般利用平移变换对应的坐标变化规律进行. 链接4 [桂林中考]如图3-Z-15, 在网格中, 每个
小正方形的边长均为1个单位长度, 我们将小正
方形的顶点叫作格点, 线段AB的端点均在格点上.
(1)将线段AB向右平移3个单位长度, 得到线段
A′B′, 画出平移后的线段并连接AB′和A′B, 两线
段相交于点O;
(2)求证:△AOB≌△B′OA′.解 (1)如图3-Z-16所示.
(2)证明:由平移的性质, 得AB∥A′B′, AB=A′B′,
∴∠BAO=∠A′B′O, ∠ABO=∠B′A′O.
在△AOB和△B′OA′中,
∵∠BAO=∠A′B′O, AB=B′A′, ∠ABO=∠B′A′O,
∴△AOB≌△B′OA′.母题4 (教材P80习题3.5第3题)
如图3-Z-17, 你能对(甲)图案进行适当的运动变化, 使它与(乙)图案重合吗?写出你的操作过程.考点:旋转作图.
考情:旋转作图是近几年中考的常考内容, 以解答题的形式出现, 常与轴对称、中心对称等相结合在网格或平面直角坐标系中考查.
策略:旋转作图的关键是确定原图形上的关键点及其关于旋转中心的对称点.链接5 [丹东中考]在平面直角坐标系中,
△ABC的位置如图3-Z-18所示(每个小方格
都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长
度, 画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°, 画出
旋转后得到的△AB2C2, 并直接写出点B2, C2
的坐标.分析 (1)利用点平移的规律写出点A, B, C的对应点A1, B1, C1的坐标, 然后描点并连线即可得到△A1B1C1;
(2)利用网格特点和旋转的性质描出点B, C的对应点B2, C2, 从而得到△AB2C2, 再写出点B2, C2的坐标.解 (1)如图3-Z-19, △A1B1C1即为所求;
(2)如图3-Z-19, △AB2C2即为所求, 点B2(4,-2), C2(1, -3).母题5(教材P86习题3.7第1题)
利用旋转分析下列图案, 并设计一个你喜欢的徽标.考点:图案设计.
考情:利用平移、轴对称或中心对称进行图案设计是中考的非重点考点, 但近几年在某些地方中考中的分量逐渐增加, 选择题、填空题、解答题的形式都有出现, 常利用网格图进行考查.
策略:灵活运用图形的平移、旋转及轴对称的知识进行实际操作是解题的关键. 链接6 [宁波中考]图3-Z-21中的网格都是由9个相同的小正方形组成的, 每个网格图中有3个小正方形已涂上阴影, 请在余下的6个空白小正方形中, 按下列要求涂上阴影:
(1)选取1个涂上阴影, 使4个阴影小正方形组成一个轴对称图形, 但不是中心对称图形;
(2)选取1个涂上阴影, 使4个阴影小正方形组成一个中心对称图形, 但不是轴对称图形;(3)选取2个涂上阴影, 使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图①、图②、图③中, 均只需画出符合条件的一种情形)解 (1)答案不唯一, 如图3-Z-22, 画出其中一种即可. (2)答案不唯一, 如图3-Z-23, 画出其中一种即可.(3)答案不唯一, 如图3-Z-24, 画出其中一种即可.
谢 谢 观 看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
