人教版七年级下册数学 5.4平移 同步练习(解析版)
文档属性
| 名称 | 人教版七年级下册数学 5.4平移 同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 981.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 11:25:04 | ||
图片预览


文档简介
5.4平移
基础闯关全练
1.下列运动中,不是平移的是( )
A.电梯上人的升降
B.钟表指针的转动
C.火车在笔直的铁轨上行驶
D.起重机上物体的升降
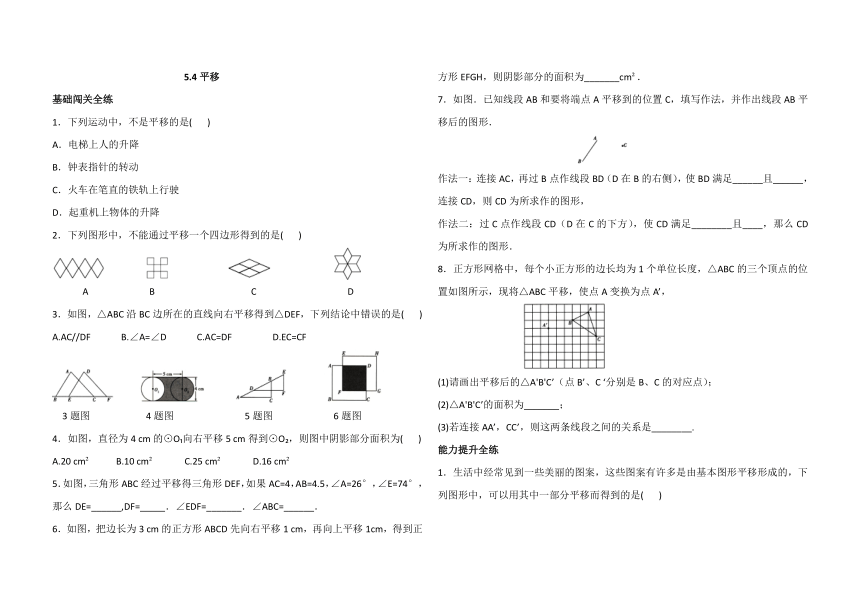
2.下列图形中,不能通过平移一个四边形得到的是( )
A B C D
3.如图,△ABC沿BC边所在的直线向右平移得到△DEF,下列结论中错误的是( )
A.AC//DF B.∠A=∠D C.AC=DF D.EC=CF
3题图 4题图 5题图 6题图
4.如图,直径为4 cm的⊙O?向右平移5 cm得到⊙O?,则图中阴影部分面积为( )
A.20 cm? B.10 cm? C.25 cm? D.16 cm?
5.如图,三角形ABC经过平移得三角形DEF,如果AC=4,AB=4.5,∠A=26°,∠E=74°,那么DE=______,DF=_____.∠EDF=_______.∠ABC=______.
6.如图,把边长为3 cm的正方形ABCD先向右平移1 cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为_______cm?.
7.如图.已知线段AB和要将端点A平移到的位置C,填写作法,并作出线段AB平移后的图形.
作法一:连接AC,再过B点作线段BD(D在B的右侧),使BD满足______且______,连接CD,则CD为所求作的图形,
作法二:过C点作线段CD(D在C的下方),使CD满足________且____,那么CD为所求作的图形.
8.正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A’,
(1)请画出平移后的△A'B'C’(点B’、C ‘分别是B、C的对应点);
(2)△A'B'C’的面积为_______;
(3)若连接AA’,CC’,则这两条线段之间的关系是________.
能力提升全练
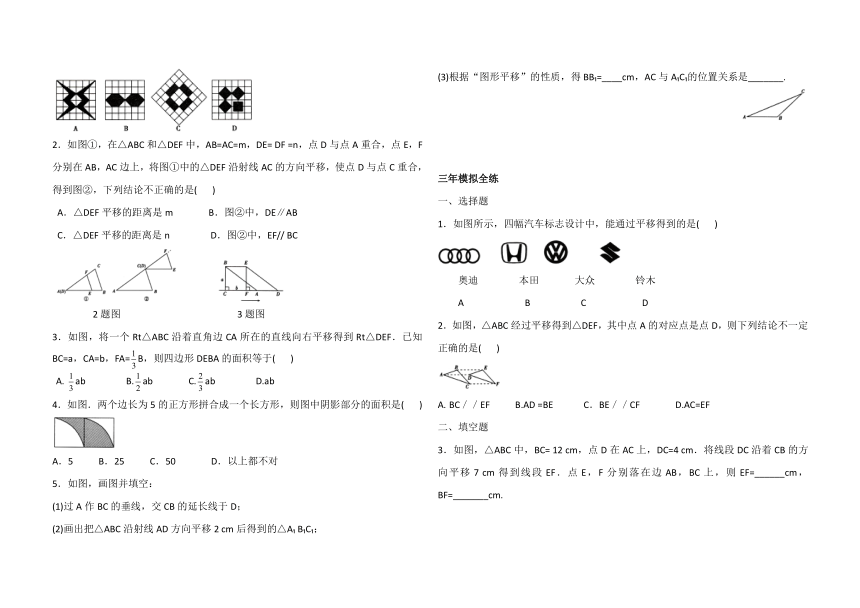
1.生活中经常见到一些美丽的图案,这些图案有许多是由基本图形平移形成的,下列图形中,可以用其中一部分平移而得到的是( )
2.如图①,在△ABC和△DEF中,AB=AC=m,DE= DF =n,点D与点A重合,点E,F分别在AB,AC边上,将图①中的△DEF沿射线AC的方向平移,使点D与点C重合,得到图②,下列结论不正确的是( )
A.△DEF平移的距离是m B.图②中,DE∥AB
C.△DEF平移的距离是n D.图②中,EF// BC
2题图 3题图
3.如图,将一个Rt△ABC沿着直角边CA所在的直线向右平移得到Rt△DEF.已知BC=a,CA=b,FA=B,则四边形DEBA的面积等于( )
ab B.ab C.ab D.ab
4.如图.两个边长为5的正方形拼合成一个长方形,则图中阴影部分的面积是( )
A.5 B.25 C.50 D.以上都不对
5.如图,画图并填空:
(1)过A作BC的垂线,交CB的延长线于D;
(2)画出把△ABC沿射线AD方向平移2 cm后得到的△A? B?C?;
(3)根据“图形平移”的性质,得BB?=____cm,AC与A?C?的位置关系是_______.
三年模拟全练
一、选择题
1.如图所示,四幅汽车标志设计中,能通过平移得到的是( )
奥迪 本田 大众 铃木
A B C D
2.如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
BC//EF B.AD =BE C.BE//CF D.AC=EF
二、填空题
3.如图,△ABC中,BC= 12 cm,点D在AC上,DC=4 cm.将线段DC沿着CB的方向平移7 cm得到线段EF.点E,F分别落在边AB,BC上,则EF=______cm,BF=_______cm.
3题图 4题图
4.如图,点O在直线MN上,∠AOB沿直线MN平移到∠CDE的位置,此时OB⊥CD于点F,若∠AOM= 58°,则∠EDN的度数为______.
五年中考全练
一、选择题
1.如图,在10 x5的网格中(每个小方格的边长为1个单位),由△ABC经过平移得到△A?B?C?,其平移过程是( )
向右平移5个单位 B.向左平移5个单位
C.向右平移6个单位 D.向左平移6个单位
2.如图,△ABC沿着BC方向平移得到△A’B’C’,点P是直线AA'上任意一点,若△ABC,△PB'C’的面积分别为S?,S?,则下列关系正确的是( )
S?>S? B.S?<S? C.S?= S? D.S?= 2S?
3.如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16 cm B.18 cm C.20 cm D.21 cm
三、填空题
4.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC’=______.
5.如图,长方形ABCD中,AB=3,BC=4.则图中四个小长方形的周长之和为______.
核心素养全练
1.如图,长方形ABCD中,AB=6.第1次平移将长方形ABCD沿AB的方向向右平移5个单位,得到长方形A?B?C?D?;第2次平移将长方形A?B?C?D?沿A?B?的方向向右平移5个单位,得到长方形A?B?C?D?;……;第n次平移将长方形沿的方向向右平移5个单位,得到长方形AnBnCnDn(n≥2).
(1)求AB?和AB?的长;
(2)若ABn的长为56,求n.
2.联想与探索
在图1①中,将线段A?A?向右平移1个单位得到线段B?B?,从而得到封闭图形A?A?B?B?,(即阴影部分);在图1②中,将折线A?A?A?向右平移1个单位得到折线B?B?B?,从而得到封闭图形A?A?A?B?B?B?(即阴影部分).
图1
(1)在图1③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形的长均为a个单位,宽均为b个单位):S?=____,S?=____,S?=____;
(3)如图2①,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位,长方形的长为a个单位,宽为b个单位),请你求出空白部分表示的草地面积是多少;
②
图2
如图2②,若在(3)的草地上又有一条横向的弯曲小路(小路任何地方的竖直宽度都是1个单位),请你求出空白部分表示的草地的面积是多少.
5.4平移
1.B根据平移的定义可知选项B不符合平移的定义.
2.D选项D不能通过平移其中一个四边形得到,需要把四边形进行旋转.
3.D ∵△ABC沿边BC所在的直线向右平移得到△DEF,∴BC=EF.∠A=∠D.AC= DF,∠ACB=∠DFE,∴BE= CF,AC∥DF.故选D.
4.A利用平移知题图中阴影部分面积=5×4= 20(cm?).故选A.
5.答案4.5;4;26°;74°
解析 通过平移得到的图形的形状和大小与原图形都相同,即对应角相等,对应边相等.
6.答案4
解析因为正方形ABCD先向右平移1 cm,再向上平移1cm,所以阴影部分是边长为3-1=2 cm的正方形,所以阴影部分的面积=2×2=4(cm?).
7.解析平行;等于AC;平行;等于AB;作图如下:
8.解析(1)平移后的△A'B'C’如图所示.
(2)=3?-×1×3-×1×2-×2×3=9-1.5-1-3=3.5.
(3)线段AA’、CC’平行且相等.
能力提升全练
1.B选项B中图形符合平移变换.故选B.
2.C在题图②中,∵AD=AC=m,∴△DEF平移的距离是m,故A结论正确,C结论错误.由平移的性质知DE∥AB、EF∥BC,故B、D结论正确.
3.C由题意可得FD=CA =b.BC=EF=a,∴AD=FD-FA=,∴四边形DEBA的面积等于AD·EF=,故选C.
4.B将左边正方形向右平移5个单位,两个正方形重合,阴影部分的面积恰是一个正方形的面积.
5.解析(1)(2)如图所示.
(3)根据“图形平移”的性质,得BB?=2 cm,AC与A?C?的位置关系是AC∥A?C?.
三年模拟全练
一、选择题
1.A根据平移的定义可知,A选项是由一个圆作为基本图形,经过平移得到的.故选A.
2.D根据平移的性质可知:BC∥EF,AD= BE,BE∥CF,AC=DF,∴选项A、B、C中结论正确,由于DF与EF大小关系不定.∴AC=EF不一定成立,故D中结论错误,故选D.
二、填空题
3.答案4;5
解析∵将线段DC沿着CB的方向平移7 cm得到线段EF,
∴EF=DC=4 cm.FC =7 cm.
∵BC= 12 cm,
∴BF=5 cm.
4.答案32°
解析由平移可得,AO∥CD,BO//ED,
∵∠AOM=58°.
∴∠CDO=58°,
又∵OB⊥CD,
∴∠BOD=32°.
∴∠EDN= ∠BOD=32°.
五年中考全练
一、选择题
1.D由图形可知△ABC向左平移6个单位得到△A?B?C?.
2.C ∵△ABC沿着BC方向平移得到△A’B’C’.∴AA'//BC.
又∵点P是直线A’上任意一点,
∴△ABC的边BC上的高与△PB’C ‘的边B'C’上的高相等,∴S?=S?,故选C.
3.C∵△ABE向右平移2 cm得到△DCF.
∴EF=AD=2 cm.AE=DF.
∵△ABE的周长为16 cm,
∴AB+BE+AE= 16 cm,
∴四边形ABFD的周长=AB+BE+EF+DF+AD =AB+BE+AE+EF+AD= 16+2+2= 20 cm.故选C.
二、填空题
4.答案5
解析由题意知,三角板向右平移了10-5=5个单位,∴顶点C平移的距离CC’=5.
5.答案14
解析把四个小长方形的各边对应向长方形ABCD的四边平移(如:把各小长方形的上方的边向AD平移),直到重合,则四个小长方形的周长之和为长方形ABCD的周长,即等于2×(3+4)=14.
核心素养全练
1.解析(1)AB?= 6+5= 11,AB?= 11+5= 16.
(2)依题意得,5n+6= 56,则n=10.
2.解析(1)图略.
(2)三个图形中所求部分的面积均为(a-1)b(提示:去掉阴影部分,则剩余部分可以拼成一个长方形).
(3)所求面积为(a-2)b.
(4)所求面积为(a-2)(b-1).
基础闯关全练
1.下列运动中,不是平移的是( )
A.电梯上人的升降
B.钟表指针的转动
C.火车在笔直的铁轨上行驶
D.起重机上物体的升降
2.下列图形中,不能通过平移一个四边形得到的是( )
A B C D
3.如图,△ABC沿BC边所在的直线向右平移得到△DEF,下列结论中错误的是( )
A.AC//DF B.∠A=∠D C.AC=DF D.EC=CF
3题图 4题图 5题图 6题图
4.如图,直径为4 cm的⊙O?向右平移5 cm得到⊙O?,则图中阴影部分面积为( )
A.20 cm? B.10 cm? C.25 cm? D.16 cm?
5.如图,三角形ABC经过平移得三角形DEF,如果AC=4,AB=4.5,∠A=26°,∠E=74°,那么DE=______,DF=_____.∠EDF=_______.∠ABC=______.
6.如图,把边长为3 cm的正方形ABCD先向右平移1 cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为_______cm?.
7.如图.已知线段AB和要将端点A平移到的位置C,填写作法,并作出线段AB平移后的图形.
作法一:连接AC,再过B点作线段BD(D在B的右侧),使BD满足______且______,连接CD,则CD为所求作的图形,
作法二:过C点作线段CD(D在C的下方),使CD满足________且____,那么CD为所求作的图形.
8.正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A’,
(1)请画出平移后的△A'B'C’(点B’、C ‘分别是B、C的对应点);
(2)△A'B'C’的面积为_______;
(3)若连接AA’,CC’,则这两条线段之间的关系是________.
能力提升全练
1.生活中经常见到一些美丽的图案,这些图案有许多是由基本图形平移形成的,下列图形中,可以用其中一部分平移而得到的是( )
2.如图①,在△ABC和△DEF中,AB=AC=m,DE= DF =n,点D与点A重合,点E,F分别在AB,AC边上,将图①中的△DEF沿射线AC的方向平移,使点D与点C重合,得到图②,下列结论不正确的是( )
A.△DEF平移的距离是m B.图②中,DE∥AB
C.△DEF平移的距离是n D.图②中,EF// BC
2题图 3题图
3.如图,将一个Rt△ABC沿着直角边CA所在的直线向右平移得到Rt△DEF.已知BC=a,CA=b,FA=B,则四边形DEBA的面积等于( )
ab B.ab C.ab D.ab
4.如图.两个边长为5的正方形拼合成一个长方形,则图中阴影部分的面积是( )
A.5 B.25 C.50 D.以上都不对
5.如图,画图并填空:
(1)过A作BC的垂线,交CB的延长线于D;
(2)画出把△ABC沿射线AD方向平移2 cm后得到的△A? B?C?;
(3)根据“图形平移”的性质,得BB?=____cm,AC与A?C?的位置关系是_______.
三年模拟全练
一、选择题
1.如图所示,四幅汽车标志设计中,能通过平移得到的是( )
奥迪 本田 大众 铃木
A B C D
2.如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
BC//EF B.AD =BE C.BE//CF D.AC=EF
二、填空题
3.如图,△ABC中,BC= 12 cm,点D在AC上,DC=4 cm.将线段DC沿着CB的方向平移7 cm得到线段EF.点E,F分别落在边AB,BC上,则EF=______cm,BF=_______cm.
3题图 4题图
4.如图,点O在直线MN上,∠AOB沿直线MN平移到∠CDE的位置,此时OB⊥CD于点F,若∠AOM= 58°,则∠EDN的度数为______.
五年中考全练
一、选择题
1.如图,在10 x5的网格中(每个小方格的边长为1个单位),由△ABC经过平移得到△A?B?C?,其平移过程是( )
向右平移5个单位 B.向左平移5个单位
C.向右平移6个单位 D.向左平移6个单位
2.如图,△ABC沿着BC方向平移得到△A’B’C’,点P是直线AA'上任意一点,若△ABC,△PB'C’的面积分别为S?,S?,则下列关系正确的是( )
S?>S? B.S?<S? C.S?= S? D.S?= 2S?
3.如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16 cm B.18 cm C.20 cm D.21 cm
三、填空题
4.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC’=______.
5.如图,长方形ABCD中,AB=3,BC=4.则图中四个小长方形的周长之和为______.
核心素养全练
1.如图,长方形ABCD中,AB=6.第1次平移将长方形ABCD沿AB的方向向右平移5个单位,得到长方形A?B?C?D?;第2次平移将长方形A?B?C?D?沿A?B?的方向向右平移5个单位,得到长方形A?B?C?D?;……;第n次平移将长方形沿的方向向右平移5个单位,得到长方形AnBnCnDn(n≥2).
(1)求AB?和AB?的长;
(2)若ABn的长为56,求n.
2.联想与探索
在图1①中,将线段A?A?向右平移1个单位得到线段B?B?,从而得到封闭图形A?A?B?B?,(即阴影部分);在图1②中,将折线A?A?A?向右平移1个单位得到折线B?B?B?,从而得到封闭图形A?A?A?B?B?B?(即阴影部分).
图1
(1)在图1③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形的长均为a个单位,宽均为b个单位):S?=____,S?=____,S?=____;
(3)如图2①,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位,长方形的长为a个单位,宽为b个单位),请你求出空白部分表示的草地面积是多少;
②
图2
如图2②,若在(3)的草地上又有一条横向的弯曲小路(小路任何地方的竖直宽度都是1个单位),请你求出空白部分表示的草地的面积是多少.
5.4平移
1.B根据平移的定义可知选项B不符合平移的定义.
2.D选项D不能通过平移其中一个四边形得到,需要把四边形进行旋转.
3.D ∵△ABC沿边BC所在的直线向右平移得到△DEF,∴BC=EF.∠A=∠D.AC= DF,∠ACB=∠DFE,∴BE= CF,AC∥DF.故选D.
4.A利用平移知题图中阴影部分面积=5×4= 20(cm?).故选A.
5.答案4.5;4;26°;74°
解析 通过平移得到的图形的形状和大小与原图形都相同,即对应角相等,对应边相等.
6.答案4
解析因为正方形ABCD先向右平移1 cm,再向上平移1cm,所以阴影部分是边长为3-1=2 cm的正方形,所以阴影部分的面积=2×2=4(cm?).
7.解析平行;等于AC;平行;等于AB;作图如下:
8.解析(1)平移后的△A'B'C’如图所示.
(2)=3?-×1×3-×1×2-×2×3=9-1.5-1-3=3.5.
(3)线段AA’、CC’平行且相等.
能力提升全练
1.B选项B中图形符合平移变换.故选B.
2.C在题图②中,∵AD=AC=m,∴△DEF平移的距离是m,故A结论正确,C结论错误.由平移的性质知DE∥AB、EF∥BC,故B、D结论正确.
3.C由题意可得FD=CA =b.BC=EF=a,∴AD=FD-FA=,∴四边形DEBA的面积等于AD·EF=,故选C.
4.B将左边正方形向右平移5个单位,两个正方形重合,阴影部分的面积恰是一个正方形的面积.
5.解析(1)(2)如图所示.
(3)根据“图形平移”的性质,得BB?=2 cm,AC与A?C?的位置关系是AC∥A?C?.
三年模拟全练
一、选择题
1.A根据平移的定义可知,A选项是由一个圆作为基本图形,经过平移得到的.故选A.
2.D根据平移的性质可知:BC∥EF,AD= BE,BE∥CF,AC=DF,∴选项A、B、C中结论正确,由于DF与EF大小关系不定.∴AC=EF不一定成立,故D中结论错误,故选D.
二、填空题
3.答案4;5
解析∵将线段DC沿着CB的方向平移7 cm得到线段EF,
∴EF=DC=4 cm.FC =7 cm.
∵BC= 12 cm,
∴BF=5 cm.
4.答案32°
解析由平移可得,AO∥CD,BO//ED,
∵∠AOM=58°.
∴∠CDO=58°,
又∵OB⊥CD,
∴∠BOD=32°.
∴∠EDN= ∠BOD=32°.
五年中考全练
一、选择题
1.D由图形可知△ABC向左平移6个单位得到△A?B?C?.
2.C ∵△ABC沿着BC方向平移得到△A’B’C’.∴AA'//BC.
又∵点P是直线A’上任意一点,
∴△ABC的边BC上的高与△PB’C ‘的边B'C’上的高相等,∴S?=S?,故选C.
3.C∵△ABE向右平移2 cm得到△DCF.
∴EF=AD=2 cm.AE=DF.
∵△ABE的周长为16 cm,
∴AB+BE+AE= 16 cm,
∴四边形ABFD的周长=AB+BE+EF+DF+AD =AB+BE+AE+EF+AD= 16+2+2= 20 cm.故选C.
二、填空题
4.答案5
解析由题意知,三角板向右平移了10-5=5个单位,∴顶点C平移的距离CC’=5.
5.答案14
解析把四个小长方形的各边对应向长方形ABCD的四边平移(如:把各小长方形的上方的边向AD平移),直到重合,则四个小长方形的周长之和为长方形ABCD的周长,即等于2×(3+4)=14.
核心素养全练
1.解析(1)AB?= 6+5= 11,AB?= 11+5= 16.
(2)依题意得,5n+6= 56,则n=10.
2.解析(1)图略.
(2)三个图形中所求部分的面积均为(a-1)b(提示:去掉阴影部分,则剩余部分可以拼成一个长方形).
(3)所求面积为(a-2)b.
(4)所求面积为(a-2)(b-1).
