四年级上册数学教案-4.5 乘法分配律北师大版
文档属性
| 名称 | 四年级上册数学教案-4.5 乘法分配律北师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览



文档简介
教学设计个人信息
姓名
单位
联系方式
设计者
史优仪
人大附中实验小学
教学基本信息
课题
乘法分配律
学科
数学
学段
第二学段
年级
四
教材
出版社:北师大出版社
1.指导思想与理论依据
新课标指出:模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号表示数学问题中的数量关系和变化规律,求出结果并讨论结果意义。
推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。
2.教学背景分析
一、教材分析
(一)从结构上看“乘法分配律的难”
乘法分配律比交换律、结合律更难于理解与应用。从结构上看交换律与结合律的只是在位置上有变化,运算上、左右算式数的多少上都没有发生变化(等号左边是几个数右边还是几个数,左边是什么运算右边仍是什么运算)。
a+b=b+a a×b=b×a (a+b)+c=a+(b+c) (a×b)×c=a×(b×c)
而乘法分配律在结构、运算和数的多少上都发生了显著的变化(等号左边是三个数,右边却是四个数;左边是+×而右边是×+×):(a+b)×c=a×c+b×c
如果把交换律与结合律等号左右两边的变化可以比喻成发生了物理反应,那乘法分配律就好像是发生了化学反应。在五条运算定律中,只有乘法分配律,沟通了乘法与加减法的联系,因此具有特殊的重要意义。
另外,交换律与结合律学生接接触比较早,更容易寻找生活模型。而乘法分配律学生接触少,或者接触了却没有感觉,因为结构本身的复杂性学生不容易找生活模型。
(二)所处领域位置
乘法分配律属于数的运算这一领域,数的运算包括运算意义、运算结果、运算定律、运算联系。而运算定律又包括交换律、结合律、分配律、减法定律、商不变性质等。加法和乘法的交换律、结合律以及乘法分配律,与四则运算联系紧密,这些基本运算律既是算理,也是运算的本质。
(三)纵向分析
1、小学整体看
关于运算律学习大致可以分为三个阶段:第一阶段也就是第一学段中,学生能够结合具体的生活实例,对运算律有所体会,在解决简单实际问题和计算题的计算中,有的学生凭借直觉有所运用,没有出现概念,是自然渗透、自觉运用阶段。
第二阶段也就是本册,系统地学习5个运算律,重点是理解运算律的意义,并运用运算律使一些运算简便,感受算式的等值变形,提升运算能力。第三阶段在五下级下册和六年级上册,主要是学习运算律在小数和分数中的应用,运用运算律使一些小数和分数的混合运算简便,提升运算能力。
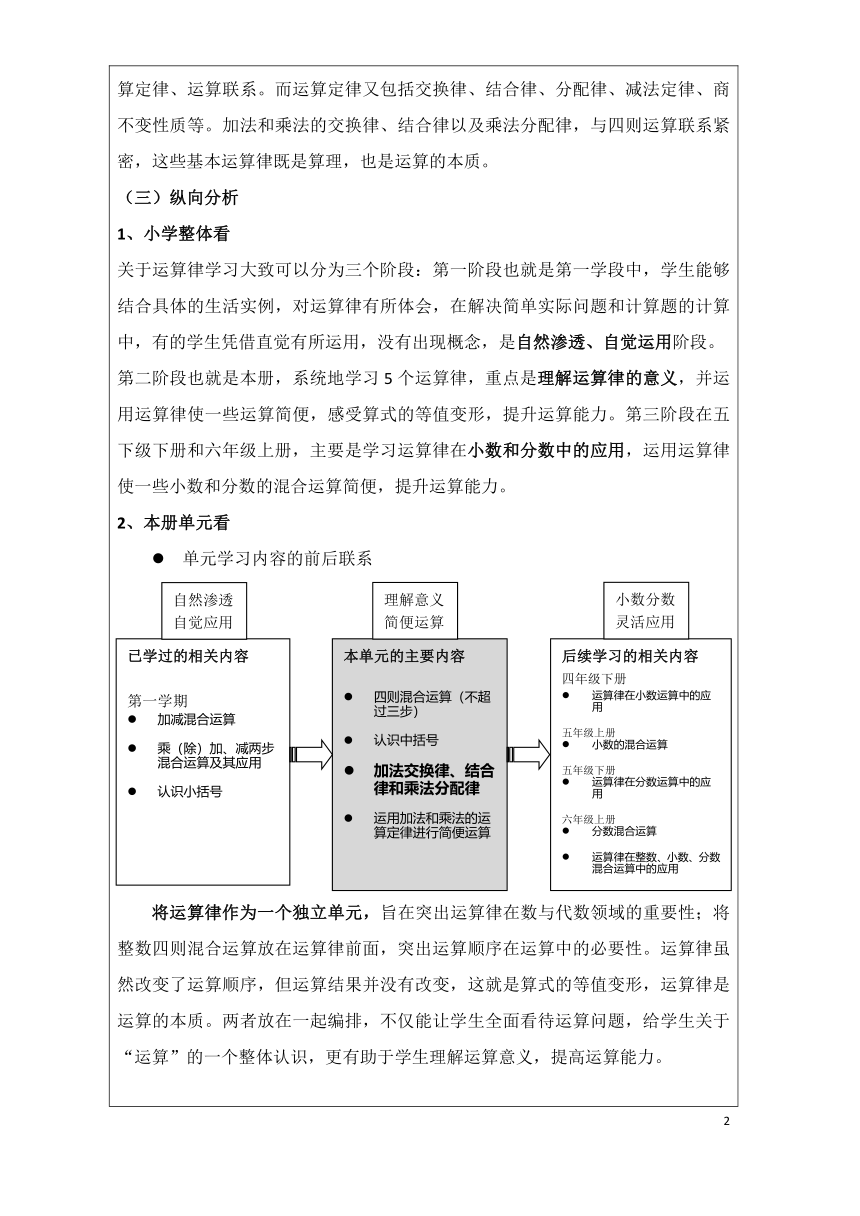
2、本册单元看
单元学习内容的前后联系
将运算律作为一个独立单元,旨在突出运算律在数与代数领域的重要性;将整数四则混合运算放在运算律前面,突出运算顺序在运算中的必要性。运算律虽然改变了运算顺序,但运算结果并没有改变,这就是算式的等值变形,运算律是运算的本质。两者放在一起编排,不仅能让学生全面看待运算问题,给学生关于“运算”的一个整体认识,更有助于学生理解运算意义,提高运算能力。
3、本课内容看
《乘法分配律》一课是在学生学习了加法交换律、加法结合律及乘法交换律、乘法结合律的基础上学习的,第一课时重在学生对乘法分配律意义的理解,之后的简便运算第二课时是在本节课理解意义的基础上学生对乘法分配律的应用。
(四)横向分析
1.相同点
(1)在学习加法和乘法的交换律、结合律的基础上学习乘法分配律。
(2)从学生的生活实际情境出发作为支持定律的模型。
(3)内容安排上都有这样的学习过程,第一是结合实际问题感受两种不同的列式计算方法;第二是从不同的列式与算法中发现乘法分配律;第三是用字母表示乘法分配律。
2.不同点
(1)北师版是在四年级上册学习,人教版和苏教版都安排在四年级下册。
(2)北师版和人教版把加法和乘法的交换律、结合律、分配律都安排在同一册书连续学习,苏教版是将加法和乘法的交换律、结合律安排在四年级上册学习,分配律则安排在四年级下册学习。
(3)在新学内容的安排上,人教版和苏教版都止步于“用字母表示乘法分配律”这个环节上,而北师版在此基础上,让学生自己已有经验再来解释说明乘法分配律的正确性。
(4)人教版特别关注了让学生找一找左右两个算式间的联系。
二、学情分析
(一)学生问题
学生往往在课堂上学习乘法分配律时还是很明白,但当进行运用乘法分配律简便运算、解决问题时,学生的问题层出不穷。就像这样的问题,我们经常会看到:
看到这些问题,不禁让我有这样的疑问:当时课堂时采用模型教学了呀!学生到底怎么了?难道当时乘法分配律的学习没有真正发生?!
(二)前测题目一
乘法分配律是乘法运算定律的重点也是教学中的一个难点。学生已经学过加法和乘法的交换律、结合律以及运用这些运算律进行简便计算,初步具备了探索和发现运算律并运用运算律进行简便计算的经验。那么结合教材分析后,学生对乘法分配律的感知到了什么程度呢?针对四(3)班36名学生进行了2个前测:
1. 请找出与(30+20)×4计算结果相等的算式, 在( )内画“√”。
① 30+20×4 ( )
② 30×4+20×4 ( )
③ 30×4+20 ( )
④ (30×4)×(20×4) ( )
2.数据分析:判断正确有24人,错误的有12人
选中的算式
人 数
百分比(%)
①30+20×4
2
5.6
②30×4+20×4
24
66.7
③30×4+20
1
2.8
④(30×4)×(20×4)
1
2.8
同时选②和④
7
19.4
空着
1
2.8
3.访谈正确的学生:你是怎么判断的?
有20人是用计算的方法,分别算一算每个算式的结果,再比较。
另4人是看算式的特点,(30+20)×4总共是50个4,而30×4+20×4就是30个4加上20个4也是50个4,所以是相等的。
(三)前测题目二
1. 请你结合生活中的例子或者学过的知识解释一下(30+20)×4和30×4+20×4是否相等,并记录下来。
2.分析
(1)能用生活中例子解释并能将两个算式之间的关系清楚表现出来的有11人,这些学生能关注到结构变化,对乘法分配律的意义有感受。
(2)仍然用计算的方式来解释的有 5 人,不能在头脑中找到相应的模型与算式匹配。
(3)能举例子但没有用生活中的例子将两个算式关系解释清楚的有20人,不能沟通算式间的联系,没有体会到结构变化与分配律的意义。
三、我的思考
乘法分配律的运算是将乘法与加减法联系起来,给学生理解增加了难度,如何让学生真正的理解而不仅仅是形式上的掌握——这很重要,也是为学生的后续应用简算、解决问题做好更坚实的铺垫!
由前测学生对乘法分配律没有真正意义上的去理解,特别是对乘法分配律两边算式的关系上学生没有感受。因此,基于教材分析与学生前测结果分析,我把本节《乘法分配律》的初始课定位在“利用模型把握乘法分配律的特点,重在理解意义”上,通过学生自主探索创造模型沟通联系,体会结构特点,积累理解乘法分配律意义的活动经验,经过抽象、推理总结出运算定律,让乘法分配律的学习真正发生。
3.教学目标(含重、难点)
教学目标:
1.经历从现实生活或具体情境中抽象出数学问题的过程,借助模型理解乘法分配律的意义。
2.经历乘法分配律的探索过程,利用多种模型体会乘法分配律的结构特点,会用
字母表示乘法分配律,积累合情推理的数学活动经验。
3.在思考、交流的过程中,培养学生抓住数学本质会倾听、会思考、会交流、善表达、善于发现问题,感受数学学习的乐趣。
教学重点:经历乘法分配律的探索过程,积累利用生活和数学模型理解乘法分配律意义的活动经验。
教学难点:结合多种模型体会乘法分配律的等式结构特点。
4.教学过程与教学资源设计(可附教学流程图)
“让乘法分配律的学习真正发生”整个教学过程经历:
5.学习效果评价设计
8×7+2×9=(8+2)×7成立吗?
请你结合右面的4幅图摆一摆,画一画,
将上面的等式修改一下,使等式成立。
6.教学设计特色说明与教学反思
1. 本节课充分体现数学核心素养之一的模型思想。模型不是老师给学生的,而是学生自己创设丰富的情境理解乘法分配律的意义,积累合情推理的思维经验。学生要从头脑中将两个算式的特点、关系进行分析,然后从头脑中调入与两个算式相区匹配的事例来解释这两个算式的关系,是学生自己创造模型理解乘法分配律意义的过程。这一过程就是学生的独立自主的对乘法分配律初次的深度认识,使学习真正的发生,是第一次深度学习。
2. 通过小组、全班交流的环节,让学生将许多不同的模型在头脑中产生化学反应,将两个算式之间的联系进行深度刻化,是对乘法分配律特点的再次深度学习
3. 全班展示的生生互动环节,让学生通过交流、倾听、思考,特别是学生经过思考后的提出问题、解答问题的过程,是将乘法分配律的本质特点充分体会,又是一次深度学习式的化学反应。
姓名
单位
联系方式
设计者
史优仪
人大附中实验小学
教学基本信息
课题
乘法分配律
学科
数学
学段
第二学段
年级
四
教材
出版社:北师大出版社
1.指导思想与理论依据
新课标指出:模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号表示数学问题中的数量关系和变化规律,求出结果并讨论结果意义。
推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。
2.教学背景分析
一、教材分析
(一)从结构上看“乘法分配律的难”
乘法分配律比交换律、结合律更难于理解与应用。从结构上看交换律与结合律的只是在位置上有变化,运算上、左右算式数的多少上都没有发生变化(等号左边是几个数右边还是几个数,左边是什么运算右边仍是什么运算)。
a+b=b+a a×b=b×a (a+b)+c=a+(b+c) (a×b)×c=a×(b×c)
而乘法分配律在结构、运算和数的多少上都发生了显著的变化(等号左边是三个数,右边却是四个数;左边是+×而右边是×+×):(a+b)×c=a×c+b×c
如果把交换律与结合律等号左右两边的变化可以比喻成发生了物理反应,那乘法分配律就好像是发生了化学反应。在五条运算定律中,只有乘法分配律,沟通了乘法与加减法的联系,因此具有特殊的重要意义。
另外,交换律与结合律学生接接触比较早,更容易寻找生活模型。而乘法分配律学生接触少,或者接触了却没有感觉,因为结构本身的复杂性学生不容易找生活模型。
(二)所处领域位置
乘法分配律属于数的运算这一领域,数的运算包括运算意义、运算结果、运算定律、运算联系。而运算定律又包括交换律、结合律、分配律、减法定律、商不变性质等。加法和乘法的交换律、结合律以及乘法分配律,与四则运算联系紧密,这些基本运算律既是算理,也是运算的本质。
(三)纵向分析
1、小学整体看
关于运算律学习大致可以分为三个阶段:第一阶段也就是第一学段中,学生能够结合具体的生活实例,对运算律有所体会,在解决简单实际问题和计算题的计算中,有的学生凭借直觉有所运用,没有出现概念,是自然渗透、自觉运用阶段。
第二阶段也就是本册,系统地学习5个运算律,重点是理解运算律的意义,并运用运算律使一些运算简便,感受算式的等值变形,提升运算能力。第三阶段在五下级下册和六年级上册,主要是学习运算律在小数和分数中的应用,运用运算律使一些小数和分数的混合运算简便,提升运算能力。
2、本册单元看
单元学习内容的前后联系
将运算律作为一个独立单元,旨在突出运算律在数与代数领域的重要性;将整数四则混合运算放在运算律前面,突出运算顺序在运算中的必要性。运算律虽然改变了运算顺序,但运算结果并没有改变,这就是算式的等值变形,运算律是运算的本质。两者放在一起编排,不仅能让学生全面看待运算问题,给学生关于“运算”的一个整体认识,更有助于学生理解运算意义,提高运算能力。
3、本课内容看
《乘法分配律》一课是在学生学习了加法交换律、加法结合律及乘法交换律、乘法结合律的基础上学习的,第一课时重在学生对乘法分配律意义的理解,之后的简便运算第二课时是在本节课理解意义的基础上学生对乘法分配律的应用。
(四)横向分析
1.相同点
(1)在学习加法和乘法的交换律、结合律的基础上学习乘法分配律。
(2)从学生的生活实际情境出发作为支持定律的模型。
(3)内容安排上都有这样的学习过程,第一是结合实际问题感受两种不同的列式计算方法;第二是从不同的列式与算法中发现乘法分配律;第三是用字母表示乘法分配律。
2.不同点
(1)北师版是在四年级上册学习,人教版和苏教版都安排在四年级下册。
(2)北师版和人教版把加法和乘法的交换律、结合律、分配律都安排在同一册书连续学习,苏教版是将加法和乘法的交换律、结合律安排在四年级上册学习,分配律则安排在四年级下册学习。
(3)在新学内容的安排上,人教版和苏教版都止步于“用字母表示乘法分配律”这个环节上,而北师版在此基础上,让学生自己已有经验再来解释说明乘法分配律的正确性。
(4)人教版特别关注了让学生找一找左右两个算式间的联系。
二、学情分析
(一)学生问题
学生往往在课堂上学习乘法分配律时还是很明白,但当进行运用乘法分配律简便运算、解决问题时,学生的问题层出不穷。就像这样的问题,我们经常会看到:
看到这些问题,不禁让我有这样的疑问:当时课堂时采用模型教学了呀!学生到底怎么了?难道当时乘法分配律的学习没有真正发生?!
(二)前测题目一
乘法分配律是乘法运算定律的重点也是教学中的一个难点。学生已经学过加法和乘法的交换律、结合律以及运用这些运算律进行简便计算,初步具备了探索和发现运算律并运用运算律进行简便计算的经验。那么结合教材分析后,学生对乘法分配律的感知到了什么程度呢?针对四(3)班36名学生进行了2个前测:
1. 请找出与(30+20)×4计算结果相等的算式, 在( )内画“√”。
① 30+20×4 ( )
② 30×4+20×4 ( )
③ 30×4+20 ( )
④ (30×4)×(20×4) ( )
2.数据分析:判断正确有24人,错误的有12人
选中的算式
人 数
百分比(%)
①30+20×4
2
5.6
②30×4+20×4
24
66.7
③30×4+20
1
2.8
④(30×4)×(20×4)
1
2.8
同时选②和④
7
19.4
空着
1
2.8
3.访谈正确的学生:你是怎么判断的?
有20人是用计算的方法,分别算一算每个算式的结果,再比较。
另4人是看算式的特点,(30+20)×4总共是50个4,而30×4+20×4就是30个4加上20个4也是50个4,所以是相等的。
(三)前测题目二
1. 请你结合生活中的例子或者学过的知识解释一下(30+20)×4和30×4+20×4是否相等,并记录下来。
2.分析
(1)能用生活中例子解释并能将两个算式之间的关系清楚表现出来的有11人,这些学生能关注到结构变化,对乘法分配律的意义有感受。
(2)仍然用计算的方式来解释的有 5 人,不能在头脑中找到相应的模型与算式匹配。
(3)能举例子但没有用生活中的例子将两个算式关系解释清楚的有20人,不能沟通算式间的联系,没有体会到结构变化与分配律的意义。
三、我的思考
乘法分配律的运算是将乘法与加减法联系起来,给学生理解增加了难度,如何让学生真正的理解而不仅仅是形式上的掌握——这很重要,也是为学生的后续应用简算、解决问题做好更坚实的铺垫!
由前测学生对乘法分配律没有真正意义上的去理解,特别是对乘法分配律两边算式的关系上学生没有感受。因此,基于教材分析与学生前测结果分析,我把本节《乘法分配律》的初始课定位在“利用模型把握乘法分配律的特点,重在理解意义”上,通过学生自主探索创造模型沟通联系,体会结构特点,积累理解乘法分配律意义的活动经验,经过抽象、推理总结出运算定律,让乘法分配律的学习真正发生。
3.教学目标(含重、难点)
教学目标:
1.经历从现实生活或具体情境中抽象出数学问题的过程,借助模型理解乘法分配律的意义。
2.经历乘法分配律的探索过程,利用多种模型体会乘法分配律的结构特点,会用
字母表示乘法分配律,积累合情推理的数学活动经验。
3.在思考、交流的过程中,培养学生抓住数学本质会倾听、会思考、会交流、善表达、善于发现问题,感受数学学习的乐趣。
教学重点:经历乘法分配律的探索过程,积累利用生活和数学模型理解乘法分配律意义的活动经验。
教学难点:结合多种模型体会乘法分配律的等式结构特点。
4.教学过程与教学资源设计(可附教学流程图)
“让乘法分配律的学习真正发生”整个教学过程经历:
5.学习效果评价设计
8×7+2×9=(8+2)×7成立吗?
请你结合右面的4幅图摆一摆,画一画,
将上面的等式修改一下,使等式成立。
6.教学设计特色说明与教学反思
1. 本节课充分体现数学核心素养之一的模型思想。模型不是老师给学生的,而是学生自己创设丰富的情境理解乘法分配律的意义,积累合情推理的思维经验。学生要从头脑中将两个算式的特点、关系进行分析,然后从头脑中调入与两个算式相区匹配的事例来解释这两个算式的关系,是学生自己创造模型理解乘法分配律意义的过程。这一过程就是学生的独立自主的对乘法分配律初次的深度认识,使学习真正的发生,是第一次深度学习。
2. 通过小组、全班交流的环节,让学生将许多不同的模型在头脑中产生化学反应,将两个算式之间的联系进行深度刻化,是对乘法分配律特点的再次深度学习
3. 全班展示的生生互动环节,让学生通过交流、倾听、思考,特别是学生经过思考后的提出问题、解答问题的过程,是将乘法分配律的本质特点充分体会,又是一次深度学习式的化学反应。
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
