人教七年级下册数学9.3一元一次不等式组 同步练习(解析版)
文档属性
| 名称 | 人教七年级下册数学9.3一元一次不等式组 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 428.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览


文档简介
9.3一元一次不等式组
1.下列不等式组中,是一元一次不等式组的是( )
A. B.
C. D.
2.不等式组的解集在数轴上表示正确的是( )
3.不等式组的解集为_____.
4.解不等式组并把解集在如图所示的数轴上表示出来,
5.解不等式组并求出它的所有整数解.
6.某商品的售价是150元,商家售出一件这种商品可获利润是进价的10%~ 20%,则进价的范围是______(精确到1元).
7.江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5 400元,有几种方案?
能力提升全练
1.不等式组的解集在数轴上表示正确的是( )
2如果关于x的不等式组的整数解仅有2和3,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有( )
A.3个 B.4个 C.5个 D.6个
3.不等式组的解集是x>-1.则a的取值范围是___________.
4.已知关于x的不等式组
(1)若a=2,求这个不等式组的解集;
(2)若这个不等式组的整数解共有3个,求a的取值范围.
5.在清江河污水网管改造建设中,需要确保在汛期来临前将建设过程中产生的渣土清运完毕,每天至少需要清运渣土12720m?.施工方准备每天租用大、小两种运输车共80辆,已知每辆大车每天运送渣土200 m?,每辆小车每天运送渣土120 m?.大、小车每天每辆租车费用分别为1 200元、900元,且要求每天租车的总费用不超过85 300元.
(1)施工方共有多少种租车方案?
(2)哪种租车方案费用最低,最低费用是多少?
三年模拟全练
一、选择题
1.不等式组的解集在数轴上表示正确的是( )
2.不等式组的最小整数解是( )
A.-1 B.0 C.1 D.2
二、填空题
3.一元一次不等式组的解集为x<-1,则a的取值范围是_______.
三、解答题
4.解不等式组并把解集在数轴上表示出来.
五年中考全练
一、选择题
1.不等式组的解集在数轴上表示正确的是( )
2.不等式组的整数解的个数是( )
A.0 B.2 C.3 D.4
3.若关于x的不等式组无解,则a的取值范围是( )
A.a≤-3 B.a<-3 C.a>3 D.a≥3
二、填空题
4.不等式组的解集为________.
三、解答题
5.解不等式组并将解集在数轴上表示出来.
6.“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102 000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员的方案?
核心素养全练
1.先阅读绝对值不等式|x|<6和|x|>6的解法,再解答下列问题:
(a)因为|x|<6,从如图所示的数轴上可以看出大于-6而小于6的数的绝对值小于6,所以|x|<6的解集为-6<x<6.
(b)因为|x|>6.从如图所示的数轴上可以看出小于-6的数和大于6的数的绝对值均大于6,所以|x|>6的解集为x>6或x<-6.
(1) |x|<3的解集为____;|x|>3的解集为__________;
(2)如果|x-5|<2,那么_______<x-5<______,所以原不等式的解集为_______,如果|x+3|>1,那么x+3>____或x+3<____,所以原不等式的解集为______.
2.某中学开学初到商场购买A,B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元.
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元;
(2)学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌的足球50个,正好赶上商场对商品价格进行调整.A种品牌的足球售价比第一次购买时提高4元,B种品牌的足球按第一次购买时售价的九折出售,如果学校要求此次购买A、B两种品牌的足球的总费用不超过第一次花费的70%,且这次购买的B种品牌的足球不少于23个,则这次学校有哪几种购买方案?
(3)请你求出学校在第二次购买活动中最多需要多少资金.
9.3一次不等式组
1.A B中含有两个未知数,C和D中的不等式组都包含不是一元一次不等式的不等式,故选A.
2.C 本题考查一元一次不等式组的解法.解不等式x+1>0可得x>-1;解不等式2x-6≤0可得x≤3,所以不等式组的解集为-1<x≤3.再根据解集在数轴上的表示方法:大于向右画,小于向左画,含等号的用实心圆点,不含等号的用空心圆圈,故选C.
3.答案
解析 解不等式3x+1≥5x,得;解不等式,得x>-3,∴不等式组的解集为.
4.解析 解不等式2x+1>x,得x>-1;解不等式,得x≤3.所以原不等式组的解集为-1<x≤3.在数轴上表示如下:
5.解析
由①得,由②得x<3,
∴此不等式组的解集为,它的所有整数解为-1,0,1,2.
6.答案125元~136元
解析 设进价为x元,则可列不等式组可得,∴进价的范围是125元~136元.
7.解析(1)设每台大型收割机1小时收割小麦a公顷,每台小型收割机1小时收割小麦b公顷,
根据题意得解得
答:每台大型收割机1小时收割小麦0.5公顷,每台小型收割机1小时收割小麦0.3公顷.
(2)设大型收割机有x台,则小型收割机有(10-x)台,根据题意得
解得5≤x≤7.
又x取整数,所以x=5,6,7,一共有三种方案.
能力提升全练
1.D解不等式①,得x>-2,解不等式②,得x≤3,在同一数轴上表示不等式①,②的解集如图所示,故选D.
2.D 解不等式组得,又∵整数解仅有2和3.∴解得又∵a,b为整数,∴a=3或4,b=9或10或11,
∴(a,b)有(3,9),(3,10),(3,11),(4,9),(4,10),(4,11),共6个.
答案
解析 分别求出每一个不等式的解集,根据口诀“同大取大”结合不等式组的解集即可确定a的范围.
4.解析(1)
解不等式①得x≤6-a,
解不等式②得x>-2,
当a=2时,不等式组的解集是-2<x≤4.
∵ 不等式组的整数解共有3个,
∴整数解是-1,0,1,
∴1≤6-a<2.
∴a的取值范围是4<a≤5.
5.解析(1)设施工方租用大车x辆,则租用小车(80-x)辆,
根据题意得解得,
∵x为整数.∴x= 39,40,41,42,43,44,∴施工方共有6种租车方案:
①租大车39辆,小车41辆;②租大车40辆,小车40辆:③租大车41辆,小车39辆;④租大车42辆,小车38辆;⑤租大车43辆,小车37辆;⑥租大车44辆,小车36辆.
(2)大、小车每天每辆租车费用分别为1200元、900元.1200>900,∴大车越少,费用越低,
∴方案①的费用最低,最低费用为39 x 1200+ 41×900=83700(元).
三年模拟全练
一、选择题
1.C 由①得x>-2,在数轴上,从数字-2处向右画,且数轴上表示-2的点画为空心圆圈;由②得x≤3,在数轴上,从数字3处向左画,且数轴上表示3的点画为实心圆点,只有选项C符合要求,故选C.
2.B 解不等式3(x+2)>2x+5得x>-1;解不等式得x≤3.所以不等式组的解集为-1<x≤3.其整数解是0,1,2,3,所以最小整数解为0.故选B.
二、填空题
3.答案 a≥-1
解析 化简不等式组,得因为不等式组的解集是x<-1,根据“同小取小”原则,可知a≥-1,故答案为a≥-1.
三、解答题
4.解析
解不等式①,得x>-1.
解不等式②,得x≤4.
所以不等式组的解集为-1<x≤4.
不等式组的解集在数轴上表示为:
五年中考全练
一、选择题
1.A 解不等式2x+1<3,得x<1;
解不等式3x+1≥-2.得x≥-1.
所以不等式组的解集为-1≤x<1.故选A.
2.C解不等式①得,x≥-1;解不等式②得,x<2,原不等式组的解集为-1≤x<2,故整数解有3个,选C.
3.A∵关于x的不等式组无解,∴a-4≥3a+2,解得a≤-3.故选A.
二、填空题
4.答案 1<x≤4
解析解不等式①,得x>1,解不等式②,得x≤4.所以这个不等式组的解集为1<x≤4.
三、解答题
5.解析解不等式①得,x>-4.解不等式②得.x≤2.
因此,原不等式组的解集为-1<x≤2.
在数轴上表示如下:
6.解析(1)设清理养鱼网箱的人均支出费用为x元,清理捕鱼网箱的人均支出费用为y元,根据题意,列方程组.得解得
答:清理养鱼网箱的人均支出费用为2 000元,清理捕鱼网箱的人均支出费用为3 000元.
(2)设清理养鱼网箱人数为m,则清理捕鱼网箱人数为(40-m),根据题意,得解得18≤m<20,∵m是整数,∴m=18或19,
∴当m=18时,40-m= 22,即清理养鱼网箱人数为18,清理捕鱼网箱人数为22:
当m=19时,40-m= 21,即清理养鱼网箱人数为19,清理捕鱼网箱人数为21.
因此,有2种分配清理人员的方案,方案一:清理养鱼网箱人数为18,清理捕鱼网箱人数为22;方案二:清理养鱼网箱人数为19,清理捕鱼网箱人数为21.
核心素养全练
1.答案(1) -3<x<3;x>3或x<-3
(2) -2;2;3<x<7;1;-1;x>-2或x<-4
2.解析(1)解法一:设购买一个A种品牌足球需x元,则购买一个B种品牌足球需(x+30)元,
由题意得50x+25(x+30)=4500,
解得x= 50.则x+30= 50+30= 80.
∴购买一个A种品牌足球需50元,购买一个B种品牌足球需80元.
解法二:设购买一个A种品牌足球需x元,购买一个B种品牌足球需y元,
由题意得解得
∴购买一个A种品牌足球需50元,购买一个B种品牌足球需80元.
(2)设购买A种品牌足球m个,则购买B种品牌足球(50-m)个,由题意得
解得25≤m≤27,又m为整数,∴m=25,26,27,∴购买方案有三种:
①购买A种品牌足球25个,购买B种品牌足球25个;
②购买A种品牌足球26个,购买B种品牌足球24个;
③购买A种品牌足球27个,购买B种品牌足球23个.
(3)方案①所需资金=25×(50+4)+0.9×80×25=3150(元);
方案②所需资金=26×(50+4)+0.9×80×24=3132(元);
方案③所需资金=27×(50+4)+0.9×80×23=3114(元).
3150>3132>3114.
∴学校在第二次购买活动中最多需要3150元资金.
1.下列不等式组中,是一元一次不等式组的是( )
A. B.
C. D.
2.不等式组的解集在数轴上表示正确的是( )
3.不等式组的解集为_____.
4.解不等式组并把解集在如图所示的数轴上表示出来,
5.解不等式组并求出它的所有整数解.
6.某商品的售价是150元,商家售出一件这种商品可获利润是进价的10%~ 20%,则进价的范围是______(精确到1元).
7.江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5 400元,有几种方案?
能力提升全练
1.不等式组的解集在数轴上表示正确的是( )
2如果关于x的不等式组的整数解仅有2和3,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有( )
A.3个 B.4个 C.5个 D.6个
3.不等式组的解集是x>-1.则a的取值范围是___________.
4.已知关于x的不等式组
(1)若a=2,求这个不等式组的解集;
(2)若这个不等式组的整数解共有3个,求a的取值范围.
5.在清江河污水网管改造建设中,需要确保在汛期来临前将建设过程中产生的渣土清运完毕,每天至少需要清运渣土12720m?.施工方准备每天租用大、小两种运输车共80辆,已知每辆大车每天运送渣土200 m?,每辆小车每天运送渣土120 m?.大、小车每天每辆租车费用分别为1 200元、900元,且要求每天租车的总费用不超过85 300元.
(1)施工方共有多少种租车方案?
(2)哪种租车方案费用最低,最低费用是多少?
三年模拟全练
一、选择题
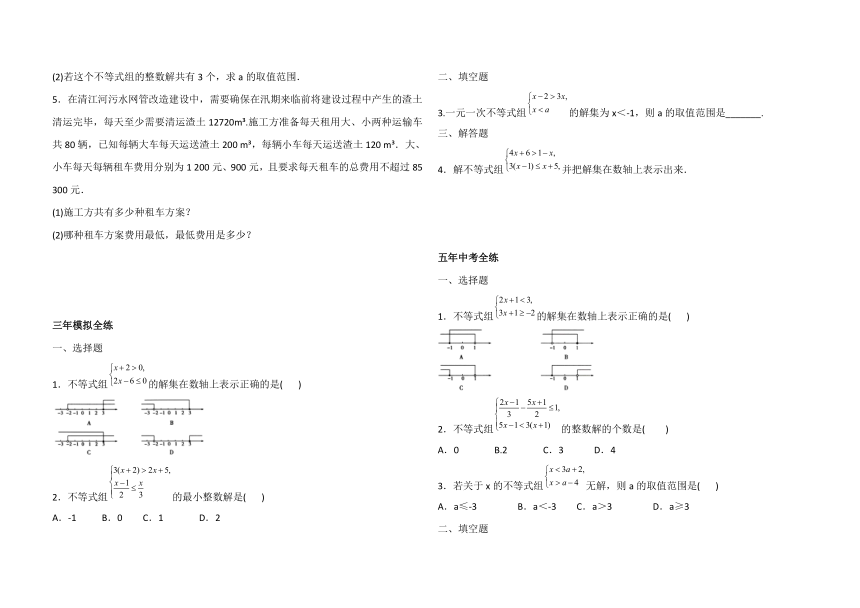
1.不等式组的解集在数轴上表示正确的是( )
2.不等式组的最小整数解是( )
A.-1 B.0 C.1 D.2
二、填空题
3.一元一次不等式组的解集为x<-1,则a的取值范围是_______.
三、解答题
4.解不等式组并把解集在数轴上表示出来.
五年中考全练
一、选择题
1.不等式组的解集在数轴上表示正确的是( )
2.不等式组的整数解的个数是( )
A.0 B.2 C.3 D.4
3.若关于x的不等式组无解,则a的取值范围是( )
A.a≤-3 B.a<-3 C.a>3 D.a≥3
二、填空题
4.不等式组的解集为________.
三、解答题
5.解不等式组并将解集在数轴上表示出来.
6.“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102 000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员的方案?
核心素养全练
1.先阅读绝对值不等式|x|<6和|x|>6的解法,再解答下列问题:
(a)因为|x|<6,从如图所示的数轴上可以看出大于-6而小于6的数的绝对值小于6,所以|x|<6的解集为-6<x<6.
(b)因为|x|>6.从如图所示的数轴上可以看出小于-6的数和大于6的数的绝对值均大于6,所以|x|>6的解集为x>6或x<-6.
(1) |x|<3的解集为____;|x|>3的解集为__________;
(2)如果|x-5|<2,那么_______<x-5<______,所以原不等式的解集为_______,如果|x+3|>1,那么x+3>____或x+3<____,所以原不等式的解集为______.
2.某中学开学初到商场购买A,B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元.
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元;
(2)学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌的足球50个,正好赶上商场对商品价格进行调整.A种品牌的足球售价比第一次购买时提高4元,B种品牌的足球按第一次购买时售价的九折出售,如果学校要求此次购买A、B两种品牌的足球的总费用不超过第一次花费的70%,且这次购买的B种品牌的足球不少于23个,则这次学校有哪几种购买方案?
(3)请你求出学校在第二次购买活动中最多需要多少资金.
9.3一次不等式组
1.A B中含有两个未知数,C和D中的不等式组都包含不是一元一次不等式的不等式,故选A.
2.C 本题考查一元一次不等式组的解法.解不等式x+1>0可得x>-1;解不等式2x-6≤0可得x≤3,所以不等式组的解集为-1<x≤3.再根据解集在数轴上的表示方法:大于向右画,小于向左画,含等号的用实心圆点,不含等号的用空心圆圈,故选C.
3.答案
解析 解不等式3x+1≥5x,得;解不等式,得x>-3,∴不等式组的解集为.
4.解析 解不等式2x+1>x,得x>-1;解不等式,得x≤3.所以原不等式组的解集为-1<x≤3.在数轴上表示如下:
5.解析
由①得,由②得x<3,
∴此不等式组的解集为,它的所有整数解为-1,0,1,2.
6.答案125元~136元
解析 设进价为x元,则可列不等式组可得,∴进价的范围是125元~136元.
7.解析(1)设每台大型收割机1小时收割小麦a公顷,每台小型收割机1小时收割小麦b公顷,
根据题意得解得
答:每台大型收割机1小时收割小麦0.5公顷,每台小型收割机1小时收割小麦0.3公顷.
(2)设大型收割机有x台,则小型收割机有(10-x)台,根据题意得
解得5≤x≤7.
又x取整数,所以x=5,6,7,一共有三种方案.
能力提升全练
1.D解不等式①,得x>-2,解不等式②,得x≤3,在同一数轴上表示不等式①,②的解集如图所示,故选D.
2.D 解不等式组得,又∵整数解仅有2和3.∴解得又∵a,b为整数,∴a=3或4,b=9或10或11,
∴(a,b)有(3,9),(3,10),(3,11),(4,9),(4,10),(4,11),共6个.
答案
解析 分别求出每一个不等式的解集,根据口诀“同大取大”结合不等式组的解集即可确定a的范围.
4.解析(1)
解不等式①得x≤6-a,
解不等式②得x>-2,
当a=2时,不等式组的解集是-2<x≤4.
∵ 不等式组的整数解共有3个,
∴整数解是-1,0,1,
∴1≤6-a<2.
∴a的取值范围是4<a≤5.
5.解析(1)设施工方租用大车x辆,则租用小车(80-x)辆,
根据题意得解得,
∵x为整数.∴x= 39,40,41,42,43,44,∴施工方共有6种租车方案:
①租大车39辆,小车41辆;②租大车40辆,小车40辆:③租大车41辆,小车39辆;④租大车42辆,小车38辆;⑤租大车43辆,小车37辆;⑥租大车44辆,小车36辆.
(2)大、小车每天每辆租车费用分别为1200元、900元.1200>900,∴大车越少,费用越低,
∴方案①的费用最低,最低费用为39 x 1200+ 41×900=83700(元).
三年模拟全练
一、选择题
1.C 由①得x>-2,在数轴上,从数字-2处向右画,且数轴上表示-2的点画为空心圆圈;由②得x≤3,在数轴上,从数字3处向左画,且数轴上表示3的点画为实心圆点,只有选项C符合要求,故选C.
2.B 解不等式3(x+2)>2x+5得x>-1;解不等式得x≤3.所以不等式组的解集为-1<x≤3.其整数解是0,1,2,3,所以最小整数解为0.故选B.
二、填空题
3.答案 a≥-1
解析 化简不等式组,得因为不等式组的解集是x<-1,根据“同小取小”原则,可知a≥-1,故答案为a≥-1.
三、解答题
4.解析
解不等式①,得x>-1.
解不等式②,得x≤4.
所以不等式组的解集为-1<x≤4.
不等式组的解集在数轴上表示为:
五年中考全练
一、选择题
1.A 解不等式2x+1<3,得x<1;
解不等式3x+1≥-2.得x≥-1.
所以不等式组的解集为-1≤x<1.故选A.
2.C解不等式①得,x≥-1;解不等式②得,x<2,原不等式组的解集为-1≤x<2,故整数解有3个,选C.
3.A∵关于x的不等式组无解,∴a-4≥3a+2,解得a≤-3.故选A.
二、填空题
4.答案 1<x≤4
解析解不等式①,得x>1,解不等式②,得x≤4.所以这个不等式组的解集为1<x≤4.
三、解答题
5.解析解不等式①得,x>-4.解不等式②得.x≤2.
因此,原不等式组的解集为-1<x≤2.
在数轴上表示如下:
6.解析(1)设清理养鱼网箱的人均支出费用为x元,清理捕鱼网箱的人均支出费用为y元,根据题意,列方程组.得解得
答:清理养鱼网箱的人均支出费用为2 000元,清理捕鱼网箱的人均支出费用为3 000元.
(2)设清理养鱼网箱人数为m,则清理捕鱼网箱人数为(40-m),根据题意,得解得18≤m<20,∵m是整数,∴m=18或19,
∴当m=18时,40-m= 22,即清理养鱼网箱人数为18,清理捕鱼网箱人数为22:
当m=19时,40-m= 21,即清理养鱼网箱人数为19,清理捕鱼网箱人数为21.
因此,有2种分配清理人员的方案,方案一:清理养鱼网箱人数为18,清理捕鱼网箱人数为22;方案二:清理养鱼网箱人数为19,清理捕鱼网箱人数为21.
核心素养全练
1.答案(1) -3<x<3;x>3或x<-3
(2) -2;2;3<x<7;1;-1;x>-2或x<-4
2.解析(1)解法一:设购买一个A种品牌足球需x元,则购买一个B种品牌足球需(x+30)元,
由题意得50x+25(x+30)=4500,
解得x= 50.则x+30= 50+30= 80.
∴购买一个A种品牌足球需50元,购买一个B种品牌足球需80元.
解法二:设购买一个A种品牌足球需x元,购买一个B种品牌足球需y元,
由题意得解得
∴购买一个A种品牌足球需50元,购买一个B种品牌足球需80元.
(2)设购买A种品牌足球m个,则购买B种品牌足球(50-m)个,由题意得
解得25≤m≤27,又m为整数,∴m=25,26,27,∴购买方案有三种:
①购买A种品牌足球25个,购买B种品牌足球25个;
②购买A种品牌足球26个,购买B种品牌足球24个;
③购买A种品牌足球27个,购买B种品牌足球23个.
(3)方案①所需资金=25×(50+4)+0.9×80×25=3150(元);
方案②所需资金=26×(50+4)+0.9×80×24=3132(元);
方案③所需资金=27×(50+4)+0.9×80×23=3114(元).
3150>3132>3114.
∴学校在第二次购买活动中最多需要3150元资金.
