人教版七年级数学下册 第十章专项综合全练 从统计图表中获取信息(解析版)
文档属性
| 名称 | 人教版七年级数学下册 第十章专项综合全练 从统计图表中获取信息(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 14:36:18 | ||
图片预览


文档简介
专项综合全练 从统计图表中获取信息
解答题
1.(2018黑龙江龙东中考)为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动.现随机抽取部分同学的成绩进行统计,并绘制成如图所示的两个不完整的统计图(A表示50~60分,B表示60~70分,C表示70~80分,D表示80~90分,E表示90~100分,每组含前一个边界值,不含后一个边界值),请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a=____,并把频数分布直方图补充完整;
(2)求扇形B的圆心角度数;
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀的学生有多少人.
2.为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成如图所示的不完整的频数分布表和频数分布直方图.
分组(单位:m) 频数
1.2≤x<1.6 a
1.6≤x<2.0 12
2.0≤x<2.4 b
2.4≤x<2.8 10
请根据图表中所提供的信息,完成下列问题:
(1)表中a=____,b=____,
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人.
3.某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”“科技社团”“书画社团”“体育社团”和“其他”五项中选择一项,并将统计结果绘制成了如图所示的两个不完整的统计图表.
社会名称 人数
文学社团 18
科技社团 a
书画社团 45
体育社团 72
其他 b
请解答下列问题:
(1)a=____,b=_____,
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为_________;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
4.为庆祝建党95周年,某校团委计划在“七一”前夕举行“唱响红歌”班级歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A、B、C、D的四首备选曲目让学生选择,经过抽样调查,将采集的数据绘制成了如图所示的两幅不完整的统计图.请根据图中所提供的信息,解答下列问题:
(1)在本次抽样调查中,选择曲目代号为A的学生占抽样总数的百分比为_______;
(2)请将条形统计图补充完整;
(3)若该校共有1530名学生,根据抽样调查的结果估计全校共有多少学生选择了必唱歌曲.(要有解答过程)
5.(2017四川南充中考)在“弘扬传统文化,打造书香校园”的活动中,学校计划开展四项活动:“A-国学诵读”“B-演讲”“C-课本剧”“D-书法”,要求每位同学必须且只能参加其中一项活动.学校为了了解学生的意愿,随机调查了部分学生,结果统计如图所示.
(1)如图,希望参加活动C的占20%,希望参加活动B的占15%,则被调查的总人数为_____;扇形统计图中,希望参加活动D的所占圆心角为________度;根据题中信息补全条形统计图:
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A的有多少人.
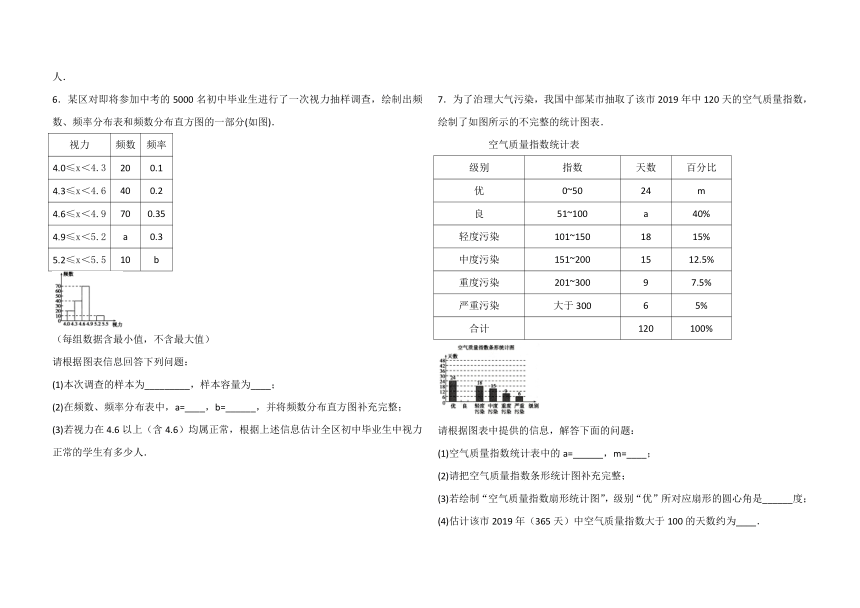
6.某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数、频率分布表和频数分布直方图的一部分(如图).
视力 频数 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(每组数据含最小值,不含最大值)
请根据图表信息回答下列问题:
(1)本次调查的样本为_________,样本容量为____;
(2)在频数、频率分布表中,a=____,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人.
7.为了治理大气污染,我国中部某市抽取了该市2019年中120天的空气质量指数,绘制了如图所示的不完整的统计图表.
空气质量指数统计表
级别 指数 天数 百分比
优 0~50 24 m
良 51~100 a 40%
轻度污染 101~150 18 15%
中度污染 151~200 15 12.5%
重度污染 201~300 9 7.5%
严重污染 大于300 6 5%
合计 120 100%
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=______,m=____;
(2)请把空气质量指数条形统计图补充完整;
(3)若绘制“空气质量指数扇形统计图”,级别“优”所对应扇形的圆心角是______度;
(4)估计该市2019年(365天)中空气质量指数大于100的天数约为____.
8.某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟所持的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果绘制了如图所示的两幅统计图.请根据图中提供的信息解答下列问题:
(1)扇形统计图中,“吸烟”所占扇形圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图;
(4)若该市共有市民760万人,求该市大约有多少人吸烟.
9.为了提高学生书写汉字的能力,增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图.
组别 成绩x/分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 6
第3组 35≤x<40 14
第4组 40≤x<45 a
第5组 45≤x<50 10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
10.(2017湖南娄底中考)为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.
专项综合全练 从统计图表中获取信息
解答题
1.解析(1)依题意得,∴样本容量=50,即一共调查了50人..∴a=30.
70~80分的频数为50-5-7-15-10=13,补充频数直方图如下:
(2)依题意得,∴扇形B的圆心角为50.4°.
(3).
答:估计获得优秀的学生有400人.
2.解析(1)由于1.2~1.6这一小组的频数为8,样本容量为50,则a=8,b=50-(8+10+12)=20.
(2)补全后的频数分布直方图如下:
(3).
答:估计九年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有200人.
3.解析(1)总人数=72÷40%=180,a=180×20%=36,b=180-18-36-45-72=9.
(2).(3).
答:估计该校学生中选择“文学社团”的有300人.
4.解析(1)本次抽样调查的总人数为.
选择曲目代号为A的学生占抽样总数的百分比为.故填20%.
(2)如图.
(3)选择曲目代号为C的人数最多,即曲目C为必唱歌曲.
所以,估计全校共有595名学生选择了必唱歌曲.
5.解析(1)被调查的总人数为12÷20%=60.
希望参加活动B的人数为60×15%=9.
希望参加活动D的人数为60-(27+9+12)=12.
扇形统计图中,D所占的圆心角为.
补全条形统计图如图所示.
(2).
则全校学生中希望参加活动A的约有360人.
6.解析(1)20÷0.1=200,则样本为抽取的200名初中毕业生的视力情况,样本容量为200.
(2)a=200×0.3=60,.补图略.
(3)估计全区初中毕业生中视力正常的学生有.
7.解析(1)a=120×40%=48,m=24÷120×100%=200%.
(2)补充完整的统计图如下:
(3)360°×20%=72°.
(4)365×(15%+12.5%+7.5%+5%)=146.
8.解析(1)“吸烟”所占扇形圆心角的度数是360°×(1-85%)=54°.
(2)这次被调查的市民人数是(80+60+30)÷85%=200.
(3)持B态度的吸烟人数是200-(80+60+30+8+12)=10.
补全条形统计图如图所示,
(4)760×(1-85%)=114(万人).
答:该市大约有114万人吸烟.
9.解析(1)a=16.
(2)如图所示:
(3)本次测试的优秀率为.
10.解析(1)162÷18%=900,∴被抽查的学生共有900人.
(2)选考历史的人数:900×6%=54.
补充完整的统计图如下:
(3)
答:估计我市九年级学生首选科目是物理的有8000人.
解答题
1.(2018黑龙江龙东中考)为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动.现随机抽取部分同学的成绩进行统计,并绘制成如图所示的两个不完整的统计图(A表示50~60分,B表示60~70分,C表示70~80分,D表示80~90分,E表示90~100分,每组含前一个边界值,不含后一个边界值),请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a=____,并把频数分布直方图补充完整;
(2)求扇形B的圆心角度数;
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀的学生有多少人.
2.为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成如图所示的不完整的频数分布表和频数分布直方图.
分组(单位:m) 频数
1.2≤x<1.6 a
1.6≤x<2.0 12
2.0≤x<2.4 b
2.4≤x<2.8 10
请根据图表中所提供的信息,完成下列问题:
(1)表中a=____,b=____,
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人.
3.某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”“科技社团”“书画社团”“体育社团”和“其他”五项中选择一项,并将统计结果绘制成了如图所示的两个不完整的统计图表.
社会名称 人数
文学社团 18
科技社团 a
书画社团 45
体育社团 72
其他 b
请解答下列问题:
(1)a=____,b=_____,
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为_________;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
4.为庆祝建党95周年,某校团委计划在“七一”前夕举行“唱响红歌”班级歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A、B、C、D的四首备选曲目让学生选择,经过抽样调查,将采集的数据绘制成了如图所示的两幅不完整的统计图.请根据图中所提供的信息,解答下列问题:
(1)在本次抽样调查中,选择曲目代号为A的学生占抽样总数的百分比为_______;
(2)请将条形统计图补充完整;
(3)若该校共有1530名学生,根据抽样调查的结果估计全校共有多少学生选择了必唱歌曲.(要有解答过程)
5.(2017四川南充中考)在“弘扬传统文化,打造书香校园”的活动中,学校计划开展四项活动:“A-国学诵读”“B-演讲”“C-课本剧”“D-书法”,要求每位同学必须且只能参加其中一项活动.学校为了了解学生的意愿,随机调查了部分学生,结果统计如图所示.
(1)如图,希望参加活动C的占20%,希望参加活动B的占15%,则被调查的总人数为_____;扇形统计图中,希望参加活动D的所占圆心角为________度;根据题中信息补全条形统计图:
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A的有多少人.
6.某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数、频率分布表和频数分布直方图的一部分(如图).
视力 频数 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(每组数据含最小值,不含最大值)
请根据图表信息回答下列问题:
(1)本次调查的样本为_________,样本容量为____;
(2)在频数、频率分布表中,a=____,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人.
7.为了治理大气污染,我国中部某市抽取了该市2019年中120天的空气质量指数,绘制了如图所示的不完整的统计图表.
空气质量指数统计表
级别 指数 天数 百分比
优 0~50 24 m
良 51~100 a 40%
轻度污染 101~150 18 15%
中度污染 151~200 15 12.5%
重度污染 201~300 9 7.5%
严重污染 大于300 6 5%
合计 120 100%
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=______,m=____;
(2)请把空气质量指数条形统计图补充完整;
(3)若绘制“空气质量指数扇形统计图”,级别“优”所对应扇形的圆心角是______度;
(4)估计该市2019年(365天)中空气质量指数大于100的天数约为____.
8.某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟所持的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果绘制了如图所示的两幅统计图.请根据图中提供的信息解答下列问题:
(1)扇形统计图中,“吸烟”所占扇形圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图;
(4)若该市共有市民760万人,求该市大约有多少人吸烟.
9.为了提高学生书写汉字的能力,增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图.
组别 成绩x/分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 6
第3组 35≤x<40 14
第4组 40≤x<45 a
第5组 45≤x<50 10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
10.(2017湖南娄底中考)为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.
专项综合全练 从统计图表中获取信息
解答题
1.解析(1)依题意得,∴样本容量=50,即一共调查了50人..∴a=30.
70~80分的频数为50-5-7-15-10=13,补充频数直方图如下:
(2)依题意得,∴扇形B的圆心角为50.4°.
(3).
答:估计获得优秀的学生有400人.
2.解析(1)由于1.2~1.6这一小组的频数为8,样本容量为50,则a=8,b=50-(8+10+12)=20.
(2)补全后的频数分布直方图如下:
(3).
答:估计九年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有200人.
3.解析(1)总人数=72÷40%=180,a=180×20%=36,b=180-18-36-45-72=9.
(2).(3).
答:估计该校学生中选择“文学社团”的有300人.
4.解析(1)本次抽样调查的总人数为.
选择曲目代号为A的学生占抽样总数的百分比为.故填20%.
(2)如图.
(3)选择曲目代号为C的人数最多,即曲目C为必唱歌曲.
所以,估计全校共有595名学生选择了必唱歌曲.
5.解析(1)被调查的总人数为12÷20%=60.
希望参加活动B的人数为60×15%=9.
希望参加活动D的人数为60-(27+9+12)=12.
扇形统计图中,D所占的圆心角为.
补全条形统计图如图所示.
(2).
则全校学生中希望参加活动A的约有360人.
6.解析(1)20÷0.1=200,则样本为抽取的200名初中毕业生的视力情况,样本容量为200.
(2)a=200×0.3=60,.补图略.
(3)估计全区初中毕业生中视力正常的学生有.
7.解析(1)a=120×40%=48,m=24÷120×100%=200%.
(2)补充完整的统计图如下:
(3)360°×20%=72°.
(4)365×(15%+12.5%+7.5%+5%)=146.
8.解析(1)“吸烟”所占扇形圆心角的度数是360°×(1-85%)=54°.
(2)这次被调查的市民人数是(80+60+30)÷85%=200.
(3)持B态度的吸烟人数是200-(80+60+30+8+12)=10.
补全条形统计图如图所示,
(4)760×(1-85%)=114(万人).
答:该市大约有114万人吸烟.
9.解析(1)a=16.
(2)如图所示:
(3)本次测试的优秀率为.
10.解析(1)162÷18%=900,∴被抽查的学生共有900人.
(2)选考历史的人数:900×6%=54.
补充完整的统计图如下:
(3)
答:估计我市九年级学生首选科目是物理的有8000人.
